2. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063
2. College of Marine and Energy Power Engineering, Wuhan University of Technology, Wuhan 430063, China
大型船舶推进轴系主要使用的滑动轴承,润滑油在轴和轴承之间形成润滑油膜,降低轴系运行时的摩擦力以及减小轴系和轴承的磨损,提高轴系运行的安全性和可靠性,降低设备的故障率。因此,对滑动轴承的润滑性能研究显得十分重要,国内外学者对其做了大量研究。针对稳定工况条件下轴承润滑性能的研究,黑棣等[1]研究了轴承参数对润滑特性的影响,比较了温粘效应和等温条件下的油膜力,温粘效应对轴承的油膜压力分布有较大影响。刘洋洋等[2]针对船用滑动轴承在低速水润滑工况下液膜承载能力不足导致的局部固体接触碰磨问题,研究了表面粗糙度对水润滑滑动轴承混合润滑性能的影响。张磊等[3]求解了Reynolds方程和黏温方程,对比分析了摇摆工况下2种轴承的轴心轨迹和油膜压力的变化。而在求解方法[4-6]和边界条件[7-9]等方面,国内外学者也开展了大量的工作,并且取得了很多创新性的结果。
对于非稳态工况下的研究,张胜伦等[10]同时考虑瞬态冲击载荷和轴瓦的弹性变形,模拟了舰船在风浪拍击时推进轴支承滑动轴承的润滑特性与动力学响应,研究了聚四氟乙烯(PTFE)弹性金属塑料瓦滑动轴承的最小油膜厚度、最大油膜压力和轴心轨迹随时间的变化情况。姚熊亮等[11]建立考虑轴颈惯性力的力平衡方程以及考虑油膜可压缩性的雷诺方程,计算轴承在瞬态冲击载荷如矩形脉冲、三角形脉冲以及正弦周期性载荷作用下的油膜压力特性。李震等[12]研究了轴承-转子系统在瞬态冲击载荷、正弦载荷、旋转载荷等激励条件下的共振现象。谢奕浓等[13]考虑加速过程伴随振动与冲击载荷耦合时变效应,数值模拟了UHMWPE轴承不同工况下启动时的润滑情况。
滑动轴承在稳定工况下的各个影响性能的参数研究已经比较深入和成熟,但是针对动态载荷情况下的轴承润滑性能的分析相对较少,而考虑到动态载荷参数的研究更是鲜有。
本文以某39 000DWT系列的散货船推进轴系尾轴承作为研究对象,建立滑动轴承的几何模型与有限元模型,考虑到动态载荷干扰的情况下,通过改变动态载荷的参数,即动态载荷的幅值和方向,利用仿真计算软件,对计算结果进行分析,以求得滑动轴承伴随着动态载荷的时变效应对其润滑性能的影响。
1 计算相关控制方程 1.1 滑动轴承油膜厚度一般的滑动轴承油膜厚度可表示为[14]:
| $ h = c[1 + \varepsilon \cos \theta - {\varepsilon ^2}c{\sin ^2}\theta /(2{r_j})] 。$ | (1) |
由于滑动轴承的径向间隙
| $ h = c(1 + \varepsilon \cos \theta )。$ | (2) |
式中:
滑动轴承在宏观条件下,Reynolds方程可简化为[14]:
| $ \frac{\partial }{{\partial x}}\left(\frac{{\rho {h^3}}}{\mu }\frac{{\partial p}}{{\partial x}}\right) + \frac{\partial }{{\partial z}}\left(\frac{{\rho {h^3}}}{\mu }\frac{{\partial p}}{{\partial z}}\right) = 6\frac{{\partial ({U_t}h\rho )}}{{\partial x}} + 12\rho \frac{{\partial h}}{{\partial t}}。$ | (3) |
式中:
当转子在稳定工况下运行的过程中,润滑油认为是不可压缩的流体,因此故润滑油的动力学黏度和密度为固定值,因此,雷诺方程可做进一步简化[15]:
| $ \frac{\partial }{{\partial x}}\left({h^3}\frac{{\partial p}}{{\partial x}}\right) + \frac{\partial }{{\partial z}}\left({h^3}\frac{{\partial p}}{{\partial z}}\right) = 6\mu {U_t}\frac{{\partial h}}{{\partial x}} + 12\mu \frac{{\partial h}}{{\partial t}} 。$ | (4) |
对油膜进行网格划分,并计算任意一个节点处的油膜厚度,将所得油膜厚度代入上式,可计算出每个节点处的油膜压力
| $ {F_{bu}} = \int_0^m {\int_1^n {{p_{i,j}}} } \sin {\theta _{i,j}}{\rm{d}}x{\rm{d}}z,$ | (5) |
| $ {F_{bv}} = \int_0^m {\int_1^n {{p_{i,j}}} } \cos {\theta _{i,j}}{\rm{d}}x{\rm{d}}z 。$ | (6) |
根据坐标转换可得水平与竖直方向的油膜力公式为:
| $ {F_{bx}} = - {F_{bu}}\sin \varPhi - {F_{bv}}\cos \varPhi ,$ | (7) |
| $ {F_{by}} = {F_{bu}}\cos \varPhi - {F_{bv}}\sin \varPhi。$ | (8) |
本文模型是依据某 39 000DWT系列的散货船推进轴系尾轴承所建,尾轴承的参数如表1所示,尾轴承简化结构模型如图1所示。
|
|
表 1 尾轴承的基本参数 Tab.1 Basic parameters of tail bearing |

|
图 1 尾轴承简化结构模型 Fig. 1 Simplified structural model of tail bearing |
通过Workbench前处理模块对尾轴承油膜进行几何建模并进行网格划分,如图2所示。

|
图 2 尾轴承油膜网格结构图 Fig. 2 Oil film grid structure diagram of tail bearing |
轴颈在滑动轴承中转动时会存在一定的偏心,这是由于轴颈运动时存在惯性造成的,因此会使滑动轴承的油膜厚度在某个部位很薄。虽然理论上油膜的厚度越小,相对应的油膜承载能力就越高,但是实际上间隙也不能无限缩小,油膜厚度过薄会造成轴承和转子之间润滑不足,使轴承存在干摩擦的风险。鉴于油膜的厚度对于轴承的润滑起着十分重要的作用,因此在油膜网格的划分就需要更加谨慎,网格的精确度对最后仿真计算的结果会造成一定的影响。本文将油膜网格划分为不同的区域,在轴承径向上采用了6层网格的划分,最终网格数量为553420万个,且网格质量在0.9。
2.3 基本假设与求解设置对某39 000DWT系列的散货船推进轴系尾轴承润滑性能的研究是基于宏观流体力学层面,因此在对滑动轴承油膜压力及油膜厚度进行时变的计算求解时,作出如下基本假设:1)认为滑动轴承的润滑油是一种不可压缩的流体;2)油膜的每个方向是通行的,并且润滑油的黏度和密度为常数;3)忽略船舶推进轴系轴向运动影响;4)润滑油的惯性力忽略不计;5)计算时忽略黏度随温度的变化。
滑动轴承润滑计算求解设置:1)选择压力瞬态求解器;2)离散格式为二阶迎风;3)压力插值格式采用Linear格式;4)求解算法为为SIMPLEC;5)监视器中的方程残差为 1×10−6,使计算过程中可以更好地收敛。
油膜相关参数如表2所示。
|
|
表 2 油膜相关参数 Tab.2 Oil film parameters |
设置的动态载荷为模拟海浪对船舶干扰时的动态载荷,根据文献[16-17]的研究,海浪动态载荷随时间的变化形式可用正弦曲线代替,分别施加x+、x−方向的动态载荷,上角标+、-分别表示沿、逆坐标轴方向。以x+方向上的动态载荷为例,向沿X轴坐标方向施加半正弦动态载荷,表达式为:
| $ {Q_Y} = 0,0 < t \leqslant 0.5,$ | (9) |
| $ \left\{ \begin{gathered} {Q_{{X^ + }}} = A\sin (5{\text{π}} t),0 < t \leqslant 0.2,\\ {Q_{{X^ + }}} = 0,0.2 < t \leqslant 0.5。\\ \end{gathered} \right. $ | (10) |
式中:
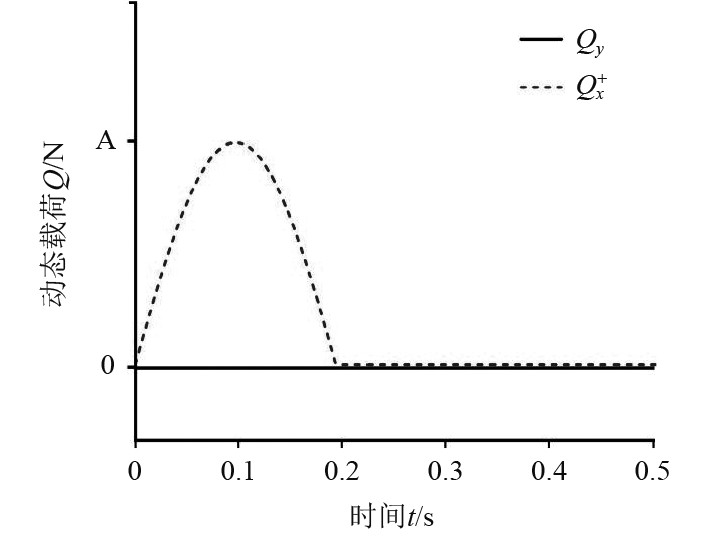
|
图 3 沿X坐标方向动态载荷示意图 Fig. 3 Dynamic load diagram along X coordinate direction |
由于仿真计算软件中对于动态载荷的设置不准确,因此要在UDF中进行动态载荷编写,将编写好的UDF导入Fluent中进行计算,编写的主要内容有控制边界运动(CG-MOTION)、边界属性(PROFILE)、更新数据(EXECUTE-AT-END)。
3 仿真计算结果分析 3.1 动态载荷幅值对轴承的润滑影响基于转子质量为2000 kg的静载荷,转速为99 r/min情况下,设定式(10)中动态载荷幅值A分别为0 N(即无动态载荷,只有静载荷的情况)、20000 N、40000 N、60000 N、80000 N、100000 N,动态载荷施加方向为x+方向。
最大油膜压力随时间的变化曲线,如图4所示。可以看出,在施加了不同幅值的动态载荷后0.5 s内,最大油膜压力的峰值随着动态载荷幅值的增大而增大,波动也更加明显。不同幅值动态载荷的最大油膜压力均在0.1 s后出现瞬时峰值,并且波动呈现出与半正弦动态载荷相似的趋势,但在0.2 s后动态载荷刚结束,最大油膜压力略有短暂的波动。出现这一变化趋势是由于开始动态载荷的作用导致油膜支撑力也随之增大,因此最大油膜压力变化趋势与施加的半正弦动态载荷相似,后由于动态载荷突然消失,油膜支撑力短时大于尾轴的作用力,因此出现短暂波动。
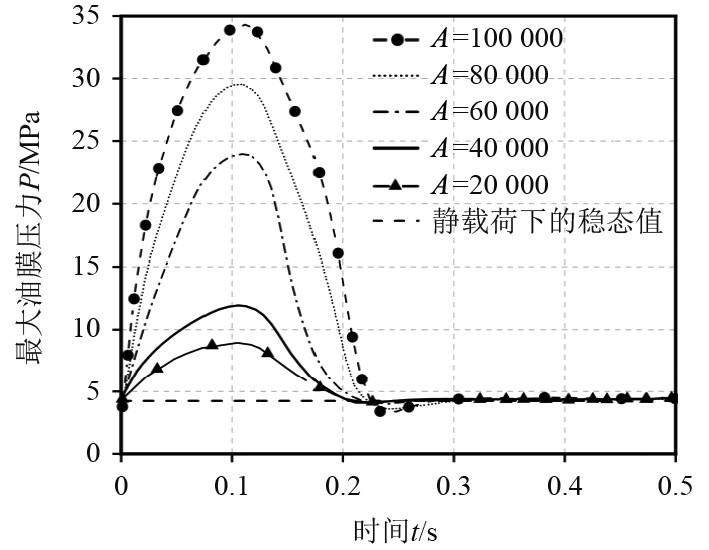
|
图 4 动态载荷幅值对最大油膜压力的影响 Fig. 4 Influence of dynamic load amplitude on maximum oil film pressure |
不同动态载荷幅值的最大油膜压力随时间变化的最大值,如表3所示。
|
|
表 3 不同动态载荷幅值最大油膜压力 Tab.3 Maximum oil film pressure with different amplitudes of dynamic load |
最小油膜厚度随时间的变化曲线,如图5所示。可以看出,在施加了不同幅值的动态载荷后0.5s内,最小油膜厚度在动态载荷施加后持续减小,但最小油膜厚度的最小值滞后动态载荷结束(0.2 s)时刻,并且随之出现短暂的上升。出现这一变化趋势是由于动态载荷作用下,尾轴载荷较大,因此最小油膜厚度先减小。但是由于尾轴的惯性力作用,在动态载荷消失过后最小油膜厚度最小值的出现滞后于动态载荷的结束时间。而由于动态载荷突然消失,而油膜的支撑力大于尾轴的载荷,将轴颈顶起,因此最小油膜厚度会出现短暂的上升。
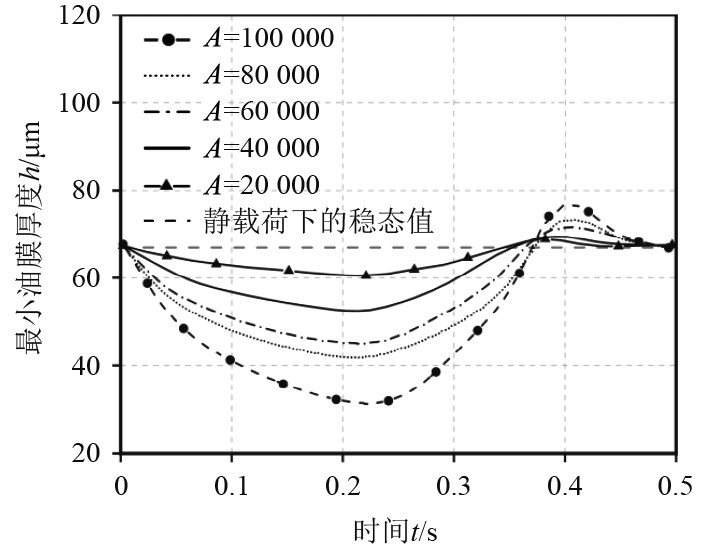
|
图 5 动态载荷幅值对最小油膜厚度的影响 Fig. 5 Influence of dynamic load amplitude on minimum oil film thickness |
不同动态载荷幅值的最小油膜厚度随时间变化的最小值,如表4所示。
|
|
表 4 不同动态载荷幅值最小油膜厚度 Tab.4 Minimum oil film thickness with different dynamic load amplitude |
基于转子质量为2000 kg的静载荷,转速为99 r/min的情况下,设定式(10)中动态载荷幅值A为60000 N,动态载荷施加方向分别为x+、x−方向。
最大油膜压力随时间的变化曲线,如图6所示。可以看出,在施加了不同方向的动态载荷后0.5 s内,不同方向动态载荷的最大油膜压力波动均呈现出与半正弦动态载荷相似的趋势,但是x+方向最大油膜压力的峰值明显高于x−方向。出现这一变化趋势是由于轴承油膜力水平方向的分力与 x+方向的载荷是正协同作用,与x−方向的载荷是负协同作用,使得x+方向最大油膜压力的峰值明显比x−方向要大,波动也更加明显。2个方向的最大油膜压力最大值分别为24.77 MPa、18.64 MPa,并最终都会趋于静载荷条件下的稳态值,即4.30 MPa。
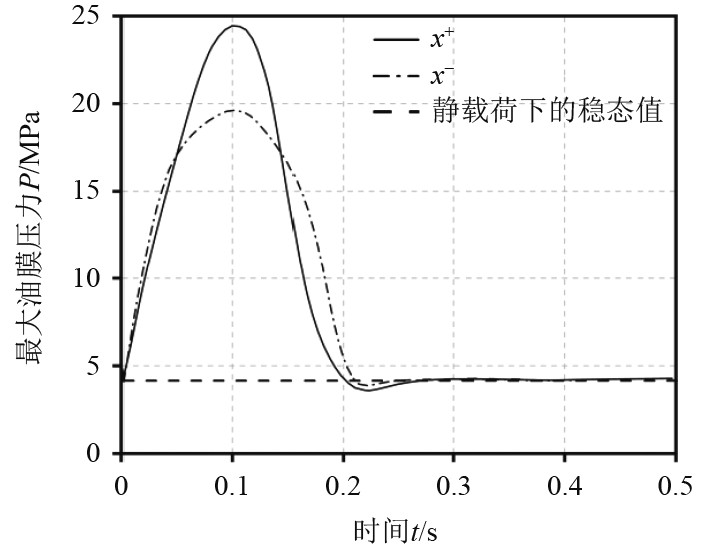
|
图 6 动态载荷方向对最大油膜压力的影响 Fig. 6 Influence of dynamic Load direction on maximum oil film pressure |
最小油膜厚度随时间的变化曲线,如图7所示。可以看出,在施加了不同幅值的动态载荷后0.5 s内,x+方向最小油膜厚度在动态载荷施加后持续减小,但最小油膜厚度的最小值滞后动态载荷结束(0.2 s)时刻,并且随之出现短暂的上升。而x−方向在受到动态载荷后最小油膜厚度则是呈现先上升后下降的趋势,这是由于动态载荷方向与轴颈油膜力水平方向的分力相反,尾轴运转的惯性力分力抵消了一部分动态载荷,导致尾轴实际载荷变小,致使油膜厚度增加的情况,0.2 s后动态载荷突然消失,油膜仅受到分力作用,且分力作用大于油膜支撑力作用,油膜厚度会短暂的下降。2个方向的最小油膜厚度最低峰值分别为47.4 μm、61.7 μm,并最终都会趋于静载荷条件下的稳态值,即67.2 μm。

|
图 7 动态载荷方向对最小油膜厚度的影响 Fig. 7 Influence of dynamic load direction on minimum oil film thickness |
本文以某 39 000DWT散货船系列的推进轴系尾轴承为研究对象,研究船舶航行过程中受到外界动态载荷干扰后,船舶尾轴承的润滑油膜特性变化规律。考虑到动态载荷的不同幅值和方向,分析滑动轴承的最大油膜压力和最小油膜厚度的时态变化,得到以下结论:
1)如载了不同幅值动态载荷后,随着动态载荷的增大,最大油膜压力随着幅值的增大而增大,且变化趋势与半正弦动态载荷趋势相似;最小油膜厚度则随着幅值的增大而减小。
2)加载了不同方向的动态载荷后,由于动态载荷与尾轴惯性力水平方向的分力的协同作用,x+方向的最大油膜压力的峰值明显高于x−方向;x+方向最小油膜厚度呈现先降低后上升的变化趋势,而x−方向呈现先上升后下降的变化趋势。
因此,当船舶航行中受到外界动态载荷干扰时,随着载荷大小和传播方向的变化,尾轴承润滑油膜的油膜压力和最小油膜厚度都在变化,当油膜压力大于油膜能承受的极限压力时,会导致油膜破裂,出现局部润滑不良甚至干摩擦的情况。因此,研究动态载荷对润滑油膜性能的影响规律,显得尤为重要。
| [1] |
黑棣, 郑美茹. 基于温粘效应滑动轴承润滑特性分析[J]. 太原科技大学学报, 2020, 41(2): 135−142.
|
| [2] |
刘洋洋, 金英泽, 王亚兵, 等. 表面粗糙度对低速水润滑滑动轴承混合润滑性能的影响[J]. 西安交通大学学报, 2020, 54(7): 121−128.
|
| [3] |
张磊, 裴世源, 徐华. 摇摆工况下两种舰船转子轴承系统的安全性与稳定性研究[J]. 中国科学: 技术科学, 2018, 48(4): 369−381.
|
| [4] |
HIRANI H, RAOTVVLNATHRE K·Rapid performance evaluation of journal bearings[J]. Tribology International, 1997, 30(11): 825−834.
|
| [5] |
IONESCU M. The analytical calculation of journal bearing parameters by means of the finite bearing theory[J]. Lubrication Science, 2011, 23: 347-353. DOI:10.1002/ls.160 |
| [6] |
SANTOS E N, BLANCO C J C, MACEDO E N, et al. Integral transform solutions for the analysis of hydrodynamic lubrication of journal bearings[J]. Tribology International, 2012, 52: 161-169. DOI:10.1016/j.triboint.2012.03.016 |
| [7] |
张俊红, 李周裕, 何振鹏, 等. 空穴效应对倾斜轴颈轴承润滑性能影响的研究[J]. 中国机械工程, 2013, 24(21): 2913-2920. DOI:10.3969/j.issn.1004-132X.2013.21.015 |
| [8] |
SHAHMOHAMADI H, RAHMANI R, RAHNEJAT H. Big end bearing losses with thermal cavitation fl-ow under cylinder deactivation[J]. Tribology Letter, 2015, 57: 1-17. DOI:10.1007/s11249-014-0447-4 |
| [9] |
苏荭, 王小静, 张直明. 动载工况下滑动轴承油膜边界历史迁移问题[J]. 机械工程学报, 2006, 42(4): 8-12. DOI:10.3321/j.issn:0577-6686.2006.04.002 |
| [10] |
张胜伦, 裴世源, 徐华, 等. 考虑瞬态冲击和弹性变形的滑动轴承特性与动力学响应[J]. 西安交通大学学报, 2018, 52(1): 100–106+114.
|
| [11] |
姚熊亮, 孙士丽, 陈玉. 高频动载轴承内油膜压力特性[J]. 机械工程学报, 2010, 46(17): 93–99.
|
| [12] |
李震, 桂长林, 李志远, 等. 变载荷作用下轴-轴承系统动力学行为研究[J]. 机械设计与研究, 2005, 21(1): 12-16. DOI:10.3969/j.issn.1006-2343.2005.01.003 |
| [13] |
谢奕浓. 海水润滑UHMWPE船舶艉轴承振动与冲击工况下启停过程润滑分析[D]. 青岛: 青岛理工大学, 2019.
|
| [14] |
张一磊, 徐武彬, 李冰, 等. 动压径向滑动轴承油膜力场的模拟与数值计算研究[J]. 机械设计与制造, 2020(1): 44–47+51.
|
| [15] |
张一磊, 徐武彬, 李冰, 等. 椭圆误差对滑动轴承转子系统运行特性的影响[J]. 机械设计与制造, 2020(2): 240–243.
|
| [16] |
黄婧. 大型集装箱船推进轴系在波浪中的动静态特性研究[D]. 武汉: 武汉理工大学, 2017.
|
| [17] |
吕芳蕊. 船用大型重载艉轴承润滑模型及结构优化的研究[D]. 上海: 上海交通大学, 2019.
|
 2023, Vol. 45
2023, Vol. 45
