舱口盖启闭装置是舰船装备的主要组成部分[1-2]。舱口盖用于弹库的水密防护,并为筒(箱)弹提供装甲防护,启闭装置功能则是依据导弹的状态执行舱口盖的开启到位或关闭、锁定等指令动作。此外,在导弹意外点火时,启闭装置需能应急打开舱口盖,为意外点火导弹提供飞离通道。因此,舱口盖启闭装置的运动控制对导弹成功发射和舰船安全性至关重要。
目前,启闭装置的传动模式主要分为液压传动[3]、螺杆传动[4]以及曲柄连杆传动[5-6]。液压传动系统受季节气候及海况影响较大,在极端情况下液压系统存在脉冲冲击、液压泄漏等不利因素,影响舱口盖系统的安全性。螺杆传动装置容易受到腐蚀。相比而言,曲柄连杆结构作为一种常见的机械式传动机构,可以方便实现复杂运动,传递较大的动力,同时便于加工生产成本低,可用于舱口盖的启闭装置中[7-8]。
殷炜棋等[9]采用Simscape对曲柄连杆机构运动轨迹进行了仿真研究,张林仙等[10-12]对内燃机曲柄连杆机构进行了动力学分析。然而,海上作业工况包括了舰艇的摇摆、风的作用等不确定因素的影响,作用于舱口盖的负载转矩随开启角度的变化而变化,导致曲柄连杆启闭机构的变化规律难以描述[13-14]。因此,本文首先对舱口盖在不同工况下的受力进行分析,并将多种工况下的受力进行叠加,通过舱口盖启闭装置的三维实体仿真模型来分析得到该多体系统的极限运动过程,从而获得了开关盖过程中启闭机构各构件的运动参数极限值。利用机构的运动参数极限值可以为舱口盖启闭装置性能优化设计以及机构电机选型提供理论指导[15]。
1 多体系统运动及动力学分析 1.1 运动学分析假设某多体系统由n个构件组成,机械系统的仿真模型将构件与构件采用运动副联接,并采用广义坐标为代数方程,则其运动学约束方程可表示为:
| $ {\varPhi ^K}(q) = {[\varPhi _1^K(q),\varPhi _2^K(q),...,\varPhi _n^K(q)]^T} = 0 $ | (1) |
假设系统中所有运动副的自由度为m, 为使系统具有确定运动,要使系统实际自由度为0,需要为系统施加m-n个驱动约束方程。同时,驱动约束通常认为是系统广义坐标系和时间的函数,表示为:
| $ {\varPhi ^D}(q,t) = {[\varPhi _1^D(q,t),\varPhi _2^D(q,t),...\varPhi _{m - n}^D(q,t)]^{\rm{T}}} = 0。$ | (2) |
由于驱动约束在其集合内部及其与运动学约束合集中是独立和相容的,此时,驱动系统将作确定运动。
由式(1)系统运动学约束和式(2)驱动约束方程组合成系统所受的全部约束,表示为:
| $ \varPhi (q,t) = \left[ {\begin{array}{*{20}{c}} {{\varPhi ^K}(q,t)} \\ {{\varPhi ^D}(q,t)} \end{array}} \right] = 0 。$ | (3) |
式(3)为m个广义坐标的非线性方程组,其构成了系统的位置方程。
对式(3)求导可得速度约束方程为:
| $ \dot \varPhi(q, \dot q, t)=\varPhi_{q}(q, t) \dot q+\varPhi_{t}(q, t)=\varPhi_{q}(q, t) \dot q-v=0 。$ | (4) |
进一步对速度约束方程(4)求导可得加速度方程:
| $\begin{split} \mathop {\mathop {\boldsymbol{\varPhi}} \limits^{ \cdot \cdot } (q,\mathop q\limits^ \cdot ,\mathop q\limits^{ \cdot \cdot } ,t)}=& {{\boldsymbol{\varPhi}} _q}(q,t)\mathop q\limits^{ \cdot \cdot } + {({{\boldsymbol{\varPhi}}_q}(q,t)\mathop q\limits^ \cdot )_q}\mathop q\limits^ \cdot +\\ & 2{{\boldsymbol{\varPhi}} _{qt}}(q,t)\mathop q\limits^ \cdot + {{\boldsymbol{\varPhi}} _{tt}}(q,t) = 0。\end{split}$ | (5) |
式中:
由式(1)~式(5)可知通过求解系统的约束方程,可获得零自由度系统的位置、速度、加速度。
1.2 动力学分析对于刚体系统,假设刚体B用质心笛卡尔坐标和反映刚体方位的欧拉角作为广义坐标可表示为:
| $ q = {\left[ {\begin{array}{*{20}{c}} x&y&z&\psi &\theta &\varphi \end{array}} \right]^{\rm{T}}} 。$ | (6) |
令:
| $ R = {\left[ {\begin{array}{*{20}{c}} x&y&z \end{array}} \right]^{\rm{T}}} ,$ | (7) |
| $ \gamma = {\left[ {\begin{array}{*{20}{c}} \psi &\theta &\varphi \end{array}} \right]^{\rm{T}}}。$ | (8) |
定义一个欧拉坐标系,该坐标系的3个单位矢量分别为3个欧拉转动的轴,该坐标系到刚体B质心坐标的转换矩阵为:
| $ B = \left[ {\begin{array}{*{20}{c}} {\sin \theta \sin \varphi }&0&{\cos \theta } \\ {\sin \theta \sin \varphi }&0&{ - \sin \theta } \\ {\cos \theta }&1&0 \end{array}} \right] 。$ | (9) |
则构件在知心笛卡尔坐标系下的角速度可表达为:
| $ \omega = B\mathop \gamma \limits^ \cdot 。$ | (10) |
系统在质心笛卡尔坐标系下的的动能可表示为:
| $ T = \frac{1}{2}{\dot R^{\rm{T}}}{\boldsymbol{M}}\dot R + \frac{1}{2}{\dot \gamma ^{\rm{T}}}{B^{\rm{T}}}{\boldsymbol{J}}B\dot \gamma 。$ | (11) |
式中:M为构件的质量矩阵;J为构件在质心坐标系下的惯量阵。
考虑约束方程的动力学方程为:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\Bigg(\frac{{\partial T}}{{\partial \mathop {{q_{}}}\limits^ \cdot }}\Bigg) - \frac{{{\partial} T}}{{{\partial} {q_{}}}} = {Q_{}} + \sum\limits_{i = 1}^n {{\lambda _i}} \frac{{{\partial} \varPhi }}{{\partial {q_{}}}} = {Q_{}} + \varPhi _q^{\rm{T}}\lambda 。$ | (12) |
式中:T为系统广义坐标表达的动能;Q为广义坐标下的广义力,最后一项为约束方程的雅可比矩阵与拉格朗日乘子,其表达了广义坐标的约束反力。
进一步引入广义动量:
| $ P = \frac{{\partial T}}{{\partial q }} 。$ | (13) |
因此,质心笛卡尔坐标系下的移动方向和转动方向动量分别表示为:
| $ {P_R} = \left( {\frac{{\partial T}}{{\partial {q_R}}}} \right) = {\boldsymbol{M}}\mathop R\limits^ \cdot,$ | (14) |
| $ {P_\gamma } = \left( {\frac{{\partial T}}{{\partial {q_\gamma }}}} \right) = {B^{\rm{T}}}{\boldsymbol{J}}B\mathop \gamma \limits^ \cdot 。$ | (15) |
设广义力为:
| $ Q = {{\boldsymbol{H}}^{\rm{T}}}F。$ | (16) |
式中,H为外力的坐标转换矩阵。
| $ F = f(q,u,t)。$ | (17) |
因此可建立质心笛卡尔坐标系下的动力学方程-微分-代数方程:
| $ \mathop p\limits^ \bullet - \frac{{\partial {{T}}}}{{\partial q}} + {\boldsymbol{\varPhi}} _q^{\rm{T}}\lambda + {{\boldsymbol{H}}^{\rm{T}}}F = 0。$ | (18) |
可知,当外力已知条件下,联合约束方程和微分-代数方程便可求解多体系统的相关运动参数。
1.3 仿真模型考虑到冲击惯性的影响,启闭装置采用实体建模,模型所用材料均采用低合金高强度结构钢,密度为7870

|
图 1 舱口盖启闭装置二维结构原理图 Fig. 1 Schematic diagram of two dimensional structure of hatch cover hoist |
启闭机构开关盖过程中,受到舰艇的摇摆、风向作用等多种不确定因素的影响。另外,作用于舱口盖的负载转矩随开启角度变化而变化。因此,模型受力分析时兼顾不同的受力工况,同时进行如下简化:
1)假设作用在舱口盖上的过载系数取模型改进舰在6 级海况下的最大摇摆载荷。
2)假设盖体在开关过程中除了开盖结构传递的动力外,其他外力包括舰艇的摇摆载荷、风阻等阻力。此情况下,舱口盖受力最为恶劣,从而可确保盖体解锁启闭机构在6级海况及任何风向时均正常工作。
3)假设舰船航行所产生的风始终平行于舰甲板,相对风速为舰的航速;自然风作为阻力始终垂直作用于舱口盖,风速为6 级海况下的自然风速。
根据上述假设,开盖与关盖过程舱口盖在其局部笛卡尔坐标系下的受力图如图2所示。
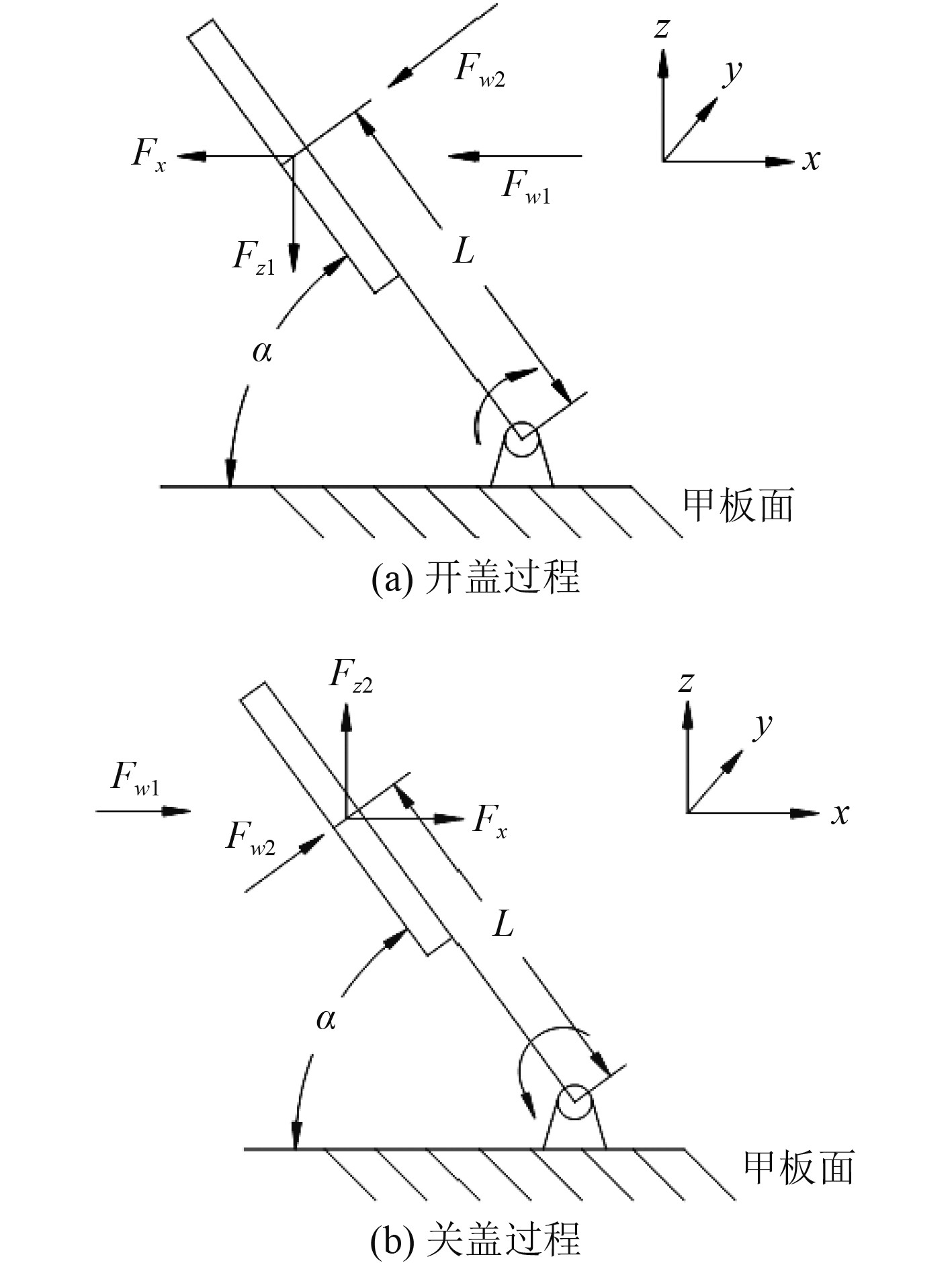
|
图 2 复杂海况下舱口盖受理分析图 Fig. 2 Analysis of hatch cover acceptance under complex sea conditions |
图中,
| $ {F_x} = {n_x}{m_g},$ | (19) |
| $ {F_z} = {n_z}{m_g} ,$ | (20) |
| $ {F_{w1(2)}} = {C_1}{k_n}{C_2}{v_{1(2)}}^2A。$ | (21) |
式中:
将上述各个方向局部坐标系下的力进行向量运算,得到在系统基本坐标系下外力矩阵为:
| $ {H^{\rm{T}}}F = {[\begin{array}{*{20}{c}} {{F_X}}&{{F_Y}}&{{F_Z}} \end{array}]^{\rm{T}}} ,$ | (22) |
式中,FX、FY、FZ 分别为启闭机构在其整体迪卡尔坐标系下X、Y、Z三方向的合力。
在笛卡尔坐标系下,将式(22)代入式(18)即可求得机构中各个部件的相关动力学参数。
1.5 结果及讨论舱口盖开启过程瞬时角度和角速度如图3所示。可以看出,舱口盖开启过程是非匀速进行的,整个过程可分为解锁-开启-锁死3个阶段。舱口盖开启最大角度为97.06°,开盖总时间约为2.4 s。

|
图 3 舱口盖开启角度与角速度-时间曲线 Fig. 3 Opening angle and angular velocity curve of hatch cover at different times |
图4为曲柄-摇杆传动比-时间曲线。可以看出,该连杆机构在解锁和锁死过程的传动比趋于无穷大值,而传动比最小值则存在于开启过程。整个开盖过程中,舱口盖、曲柄及摇杆主要运动参数汇总如表1所示。
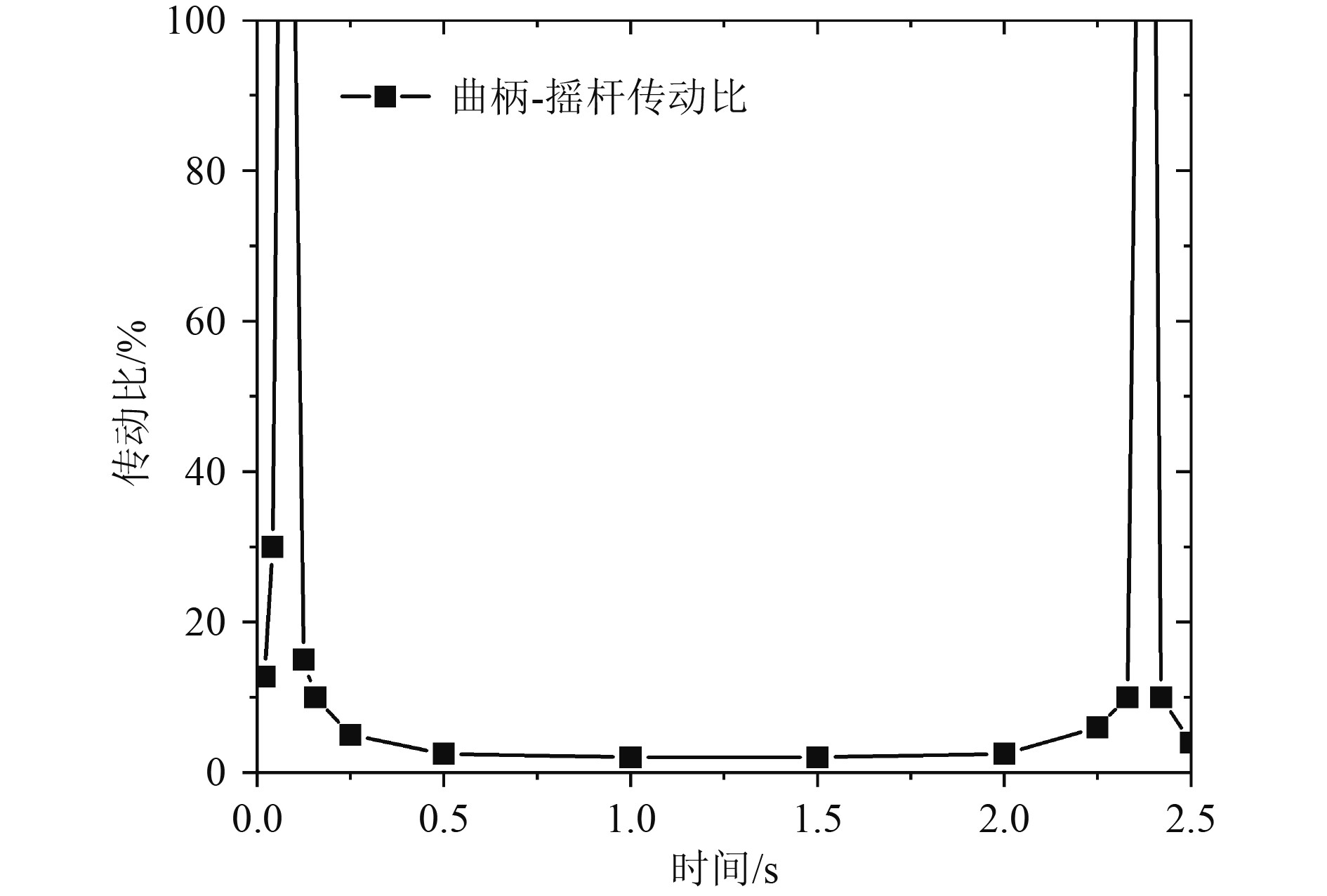
|
图 4 曲柄-摇杆传动比-时间曲线 Fig. 4 Transmission ratio curve of crank rocker at different times |
|
|
表 1 各系数及其数值汇总表 Tab.1 Summary of coefficients and their values |
另外,由于受力差异,开关盖过程中舱口盖负载转矩也存在明显差距。图5表明,开盖过程中相同时刻盖体负载力矩明显高于关盖过程。0.75 s时,开盖过程盖体负载力矩达到最大值1751 N·m,而关盖过程盖体负载力矩则在0.70 s时达到最大值856 N·m。机构中4组铰链归一化后的支反力随时间的变化曲线如图6所示。可以看出,0.25 s时,铰链A、B(C)支反力达到最大值;0.242 s时,铰链D支反力达到最大值。
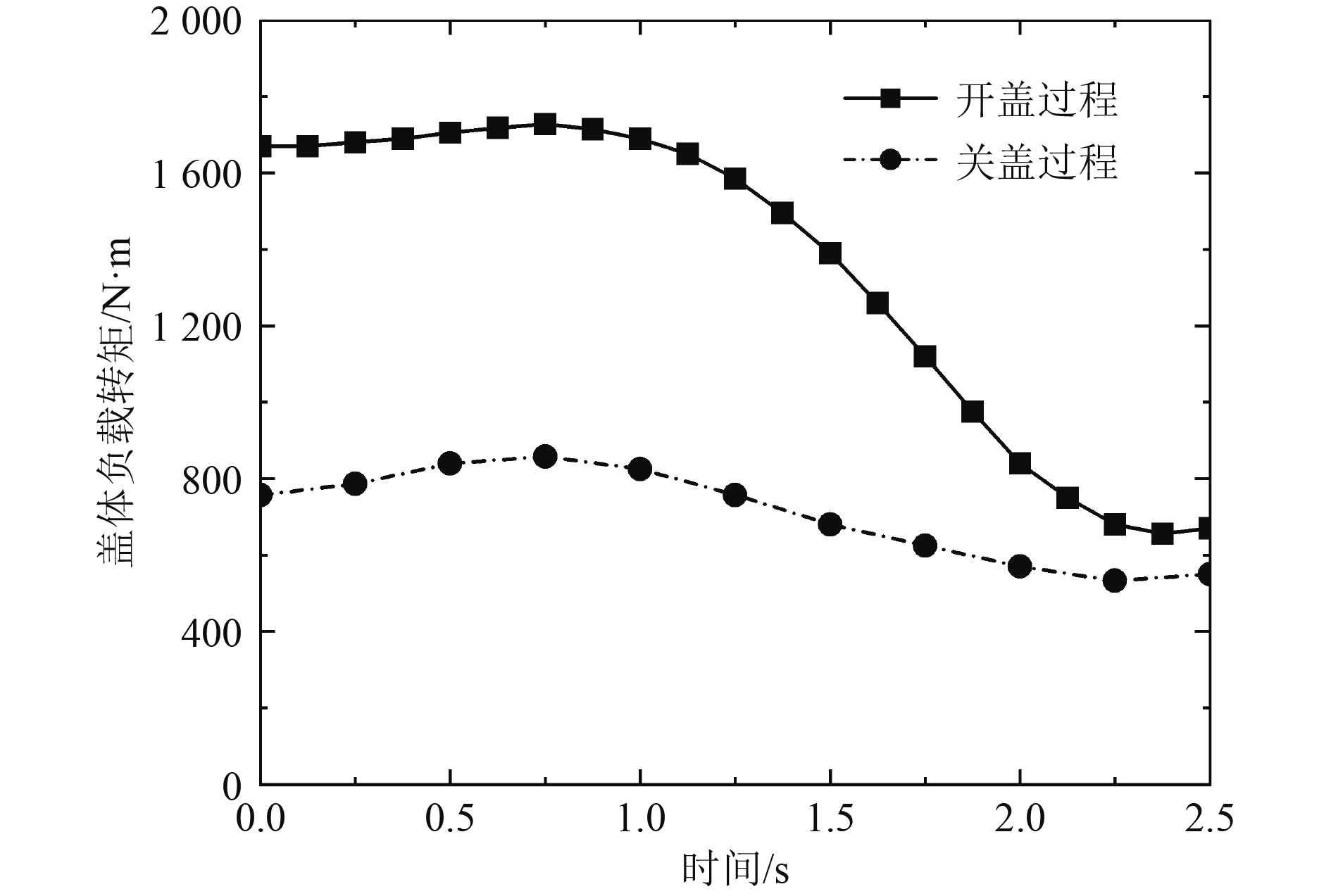
|
图 5 开关盖过程中舱口盖负载转矩-时间变化曲线 Fig. 5 Load torque curve of hatch cover at different times |
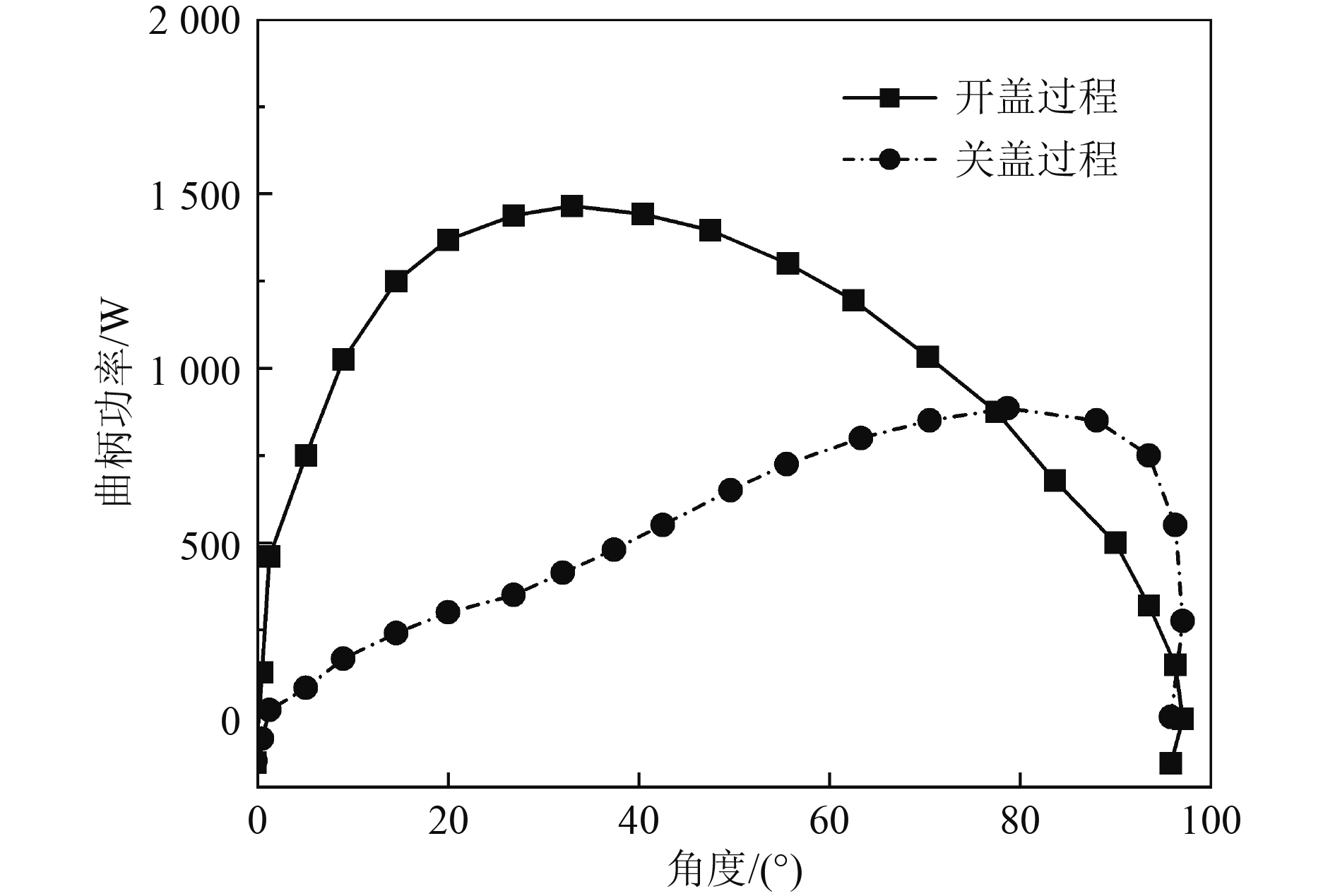
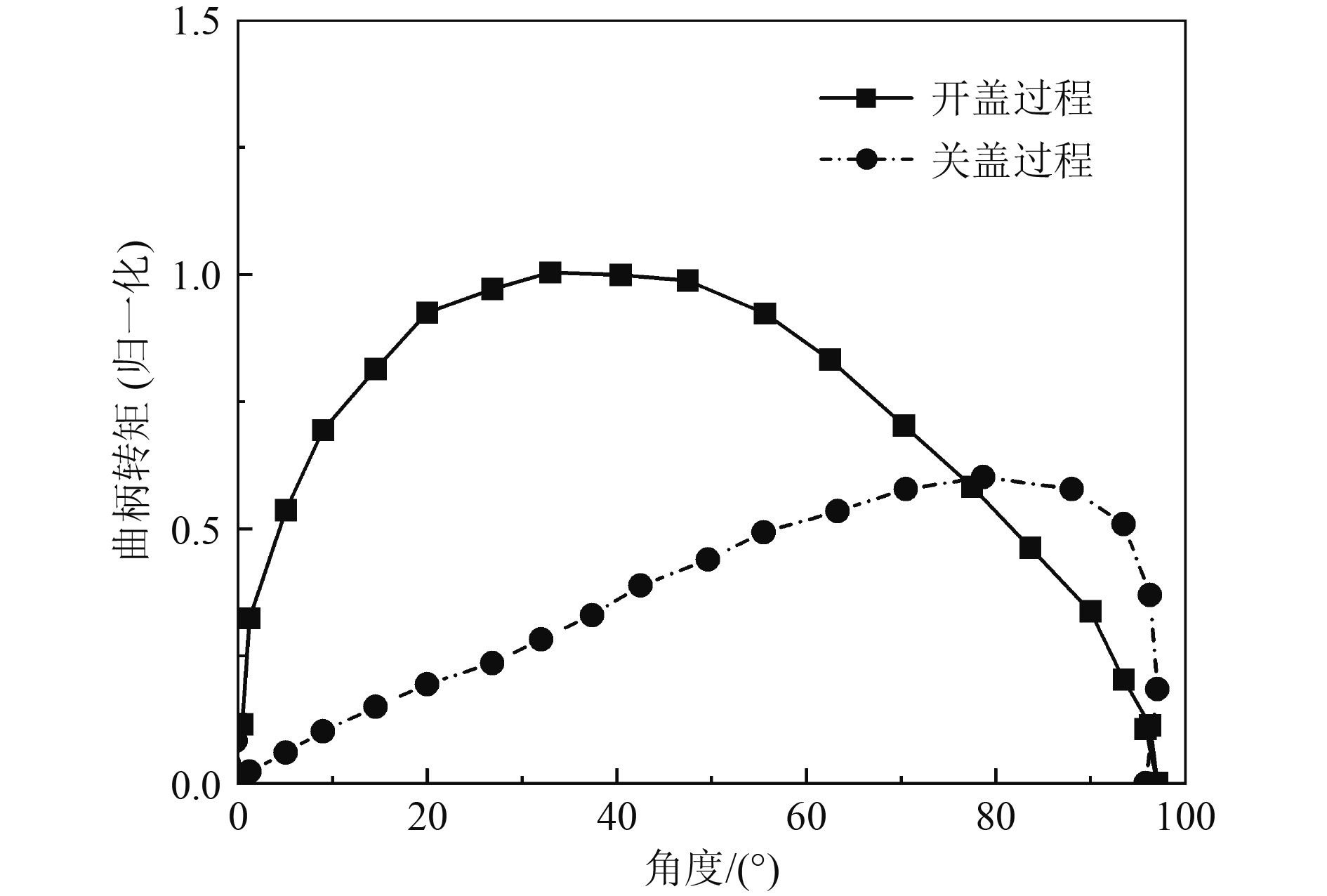
图7和图8分别为舱口盖开盖和关盖过程曲柄转矩(归一化)和曲柄功率-角度变化曲线。可以看出,开盖过程中曲柄转矩与瞬时功率远高于关盖过程;开盖角度为34.74°时,曲柄转矩和瞬时功率达到最大值。关盖角度为71.48°时,曲柄转矩和瞬时功率达到最大值。开关盖过程中,舱口盖功率最大值及其对应时间汇总如表2所示。
|
|
表 2 开关盖过程中曲柄连杆结构相关动力学参数汇总 Tab.2 Dynamic paramaters at the limit position of the hatch cover hoisiting mechanism during the process from opening and closing |

|
图 6 开关盖过程中舱口盖启闭机构中4组铰链支反力(归一化)-时间变化曲线 Fig. 6 Support reaction (normalized) curve of four groups of hinges in hatch cover hoisting mechanism at different times |
|
图 7 开关盖过程曲柄转矩(归一化)随舱口盖角度变化曲线 Fig. 7 Curve of crank torque (normalized) changing with hatch opening angle |
|
图 8 开关盖过程曲柄功率随舱口盖角度变化曲线 Fig. 8 Curve of crank power changing with hatch opening angle |
1)通过多体系统的运动学和动力学理论分析可知,对舱口盖启闭机构在开关过程的受力分析是保证仿真计算结果准确的前提条件。
2)舱口盖启闭装置仿真计算结果表明,舱口盖启闭装置用电机的最大转矩与功率都出现于开盖过程中,其最大功率值可作为电机选型的依据。
3)为确保舱口盖启闭装置可以在极端条件下正常运行,在对舱口盖受力分析时将各种可能存在的载荷取最大值并线性叠加,因此电机最大功率计算结果比实际偏高。
| [1] |
ITO K, KUROIWA T, AKAGI S. Design optimization of hatch cover opening and closing mechanism of ships. Application of minimax non-linear optimization method[J]. Transactions of the Japan Society of Mechanical Engineers, 1985, 51(462): 460-468. DOI:10.1299/kikaic.51.460 |
| [2] |
王忠强, 秦荣俊, 支山亚. 基于质量优化目标的舱口盖结构设计及强度校核[J]. 船舶, 2022, (1): 70–77.
|
| [3] |
曲志云. 922型打捞救生船的船舱口盖启闭装置[J]. 船舶, 1992, (2): 41–42.
|
| [4] |
吴韵侠, 胡修池, 高卫红. 引黄涵闸螺杆式启闭机的维护技术研究与应用[J]. 水利水电技术, 2011, 42(2): 74–75.
|
| [5] |
BATES K T, FALKINGHAM P L. Estimating maximum bite performance in Tyrannosaurus rex using multi-body dynamics [J]. Biology Letters, 2012, 8(4): 660–664.
|
| [6] |
吴楠, 廖日东, 张保成, 等. 柴油机曲柄连杆机构多体动力学仿真分析[J]. 内燃机工程, 2005, 26(5): 69–73.
|
| [7] |
刘永亮, 任克亮, 马旭轮, 等. 平面四杆机构在舰载垂直发射装置舱口盖系统中的应用分析[J]. 装备环境工程, 2019, 16(5): 13–17.
|
| [8] |
SINGH R, CHAUDHARY H, SINGH A K. Defect-free optimal synthesis of crank-rocker linkage using nature-inspired optimization algorithms[J]. Mechanism and Machine Theory, 2017, 116: 105-122. DOI:10.1016/j.mechmachtheory.2017.05.018 |
| [9] |
殷炜棋, 杨鲁义, 朱国仁. 基于Simscape的曲柄连杆机构运动轨迹仿真研究[J]. 工程与试验, 2022, 62(2): 18–21.
|
| [10] |
张林仙, 张生保. 基于多体系统仿真的内燃机曲柄连杆机构动力学分析[J]. 装备制造技术, 2006(4): 14–16.
|
| [11] |
杜爱民, 杜玉彪, 楼狄明, 等. 发动机曲柄连杆机构动力学仿真分析平台研究[J]. 计算机仿真, 2010, 27(11): 278–283.
|
| [12] |
叶奇, 孙鹏文, 张敏. 发动机曲柄连杆机构多体动力学建模的若干问题[J]. 机电工程, 2007, 24(12): 53–55.
|
| [13] |
郭亦平, 杜春旺, 李明, 等. 恶劣海况下船舶航向控制仿真及应用研究[J]. 舰船科学技术, 2008, 30(1): 142-152. GUO Y P, DU C W, LI M, et al. Simulation and research of application of ship yaw control in the bad sea condition[J]. Ship Science and Technology, 2008, 30(1): 142-152. |
| [14] |
LEPIDI M, GATTULLI V. Non-linear interactions in the flexible multi-body dynamics of cable-supported bridge cross-sections [J]. International Journal of Non-Linear Mechanics, 2016(80): 14–28.
|
| [15] |
潘爱华. 起重机起升机构电动机的选用[J]. 起重运输机械, 2006 (7): 31–34.
|
 2023, Vol. 45
2023, Vol. 45
