2. 中国特种飞行器研究所高速水动力航空科技重点实验室 湖北 荆门 448035;
3. 中国特种飞行器研究所水动力研究中心,湖北 荆门 448035
2. China Special Vehicle Research Institute Key Aviation Scientific and Technological Laboratory of High-speed Hydrodynamic, Jingmen 448035, China;
3. China Special Vehicle Research Institute Hydrodynamic Research Center, Jingmen 448035, China
火炮系统作为现代武器装备体系的重要组成部分,在现代战争中的重要性日益凸显。面对国内外日益增长的中小型舰艇火炮加装需求,如何评估火炮加装后对中小型舰艇稳定性能产生的影响成为急需解决的问题。
近年来,为维护海洋主权以及国家海洋经济稳定发展,执法巡逻艇设计技术也得到了快速发展,针对发射炮弹对巡逻艇稳定性研究成为一项重要的研究课题。高速执法艇一般在航行时完成射击,当发射大口径炮弹时,产生的后坐力必然对巡逻艇施加一个横向倾斜力矩,破坏船舶的平衡状态。尤其是在风浪条件复杂的开阔水域,巡逻艇在运动中产生摇荡,多自由度运动耦合进一步增大巡逻艇倾覆的可能性,对人员及船艇的安全性造成巨大威胁。因此,开展炮弹后坐力对高速巡逻艇的稳定性研究,对掌握高速航行状态下巡逻艇射击炮弹的安全口径范围显得尤为重要。
目前,国内外针对高速艇的横稳性主要通过数值模拟和水池试验的方式对其横稳性损失问题进行研究。一般采用固定横倾角模型试验或无航速静稳性试验[1-4],而对于高速艇在有航速的状态下也仅进行了对船体施加固定横倾力矩的横稳性数值模拟[5],鲜有学者开展瞬时外力对高速滑行艇横稳性的影响研究。本文基于模型拖曳与外力瞬时冲击耦合的方法,针对某高速滑行状态的巡逻艇模型进行多种外力作用方式下的横摇运动模拟,得到巡逻艇模型的横摇幅值及横摇衰减特性,分析不同外力形式对巡逻艇运动横稳性影响的规律,得到一种模拟炮弹后坐力对巡逻艇横稳性影响的试验分析方法。
1 试验模型及方案设计外力冲击下的巡逻艇运动横稳性试验依托中国特种飞行器研究高速水动实验室开展。其高速拖曳试验水池及其配套的拖车、造波机等高速水动力试验设备技术指标如下:
1)水池主尺度
池长510 m,池宽6.5 m,池深6.8 m,水深5.0 m。
2)拖车性能
速度范围0.1~25 m/s,车速稳定精度优于0.1%。
3)造波机性能
规则波波长0.5~15 m,波高0.03~0.50 m;各类长峰不规则波。
4)测试手段
试验数据采集和处理分析自动化。
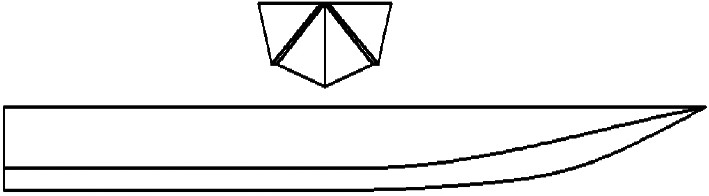
1.1 试验模型选用的高速巡逻艇模型如图1所示。船模总长L为2 840 mm,折角线宽为445 mm,排水量为128 kg,尾部的船底斜升角β为18°。在船体坐标系中,以基线为X轴,向首为正;船宽方向为Y轴,向左舷为正;垂向为Z轴,向上为正。综合各方面因素考虑,船模缩尺比选择为5∶1。
|
图 1 巡逻艇模型 Fig. 1 Planning craft model |
与常规的船模拖曳试验不同,火炮后坐力冲击下的巡逻艇运动横稳性试验除了要模拟模型定速滑行外,还要模拟在运动过程突然受到的瞬时外力冲击,因此需要对火炮后坐力的施加形式进行特殊设计。
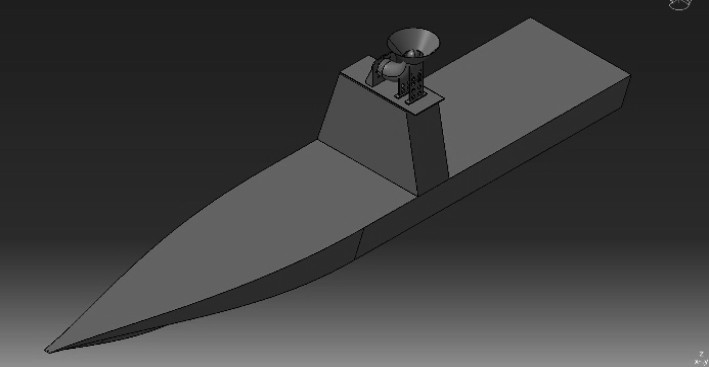
安装于巡逻艇上的武器装备在发射过程中,对艇体存在一个反作用力的作用,即为后坐力。由于火炮发射对艇体产生冲量,而冲量是力的时间累积效应的量度,为矢量,通常用于求解短暂过程(如撞击)物体间的作用力,试验较难模拟。因此,采用动量等效模拟火炮发射时的反作用力。在艇体甲板面上方搭建一个L型滑道,采用1枚球形弹丸以指定的高度自由落体。以某一水平速度敲击艇体,模拟炮弹后坐力产生的瞬时冲量,如图2所示。
|
图 2 敲击试验模型 Fig. 2 Percussive experiment model |
敲击点贴压力应变片以测量敲击力的变化时历曲线,安装在巡逻艇模型中的倾角传感器可对模型横摇角的变化进行实时测量。冲量与动量按下式进行转换:
| $ F \times t = M \times V 。$ |
式中:F为后坐力大小;t为后坐力作用时间;M为弹丸质量;V为水平敲击速度。其中V的大小通过弹丸自由落体的高度来进行控制,在试验开始前对弹丸拟达到的速度进行校核。
1.3 试验工况为研究模型状态、外力状态对巡逻艇模型横稳性的影响规律,开展不同重心位置的静水阻力试验及不同重心高度、不同冲量、不同滑行速度的敲击试验。
表1为同一排水量的模型在前、中、后3种不同重心位置的静水拖曳试验,通过对比试验结果以选择合适的重心位置开展敲击试验。
|
|
表 1 巡逻艇模型静水阻力试验工况表 Tab.1 Hydrostatic resistance conditions of model |
表2为敲击试验的工况表,工况4~工况6用以对比冲量变化对模型横稳性的影响规律,工况4与工况7用以研究模型的重心高度对横稳性的影响,工况6和工况8~工况11用以研究航速对模型运动稳定性的影响规律。
|
|
表 2 敲击试验工况表 Tab.2 Percussive experiment conditions of model |
根据试验工况计划开展模型试验,其中静水阻力试验及敲击试验工况5为带航速的拖曳试验,其余状态均为零速静水横摇试验。
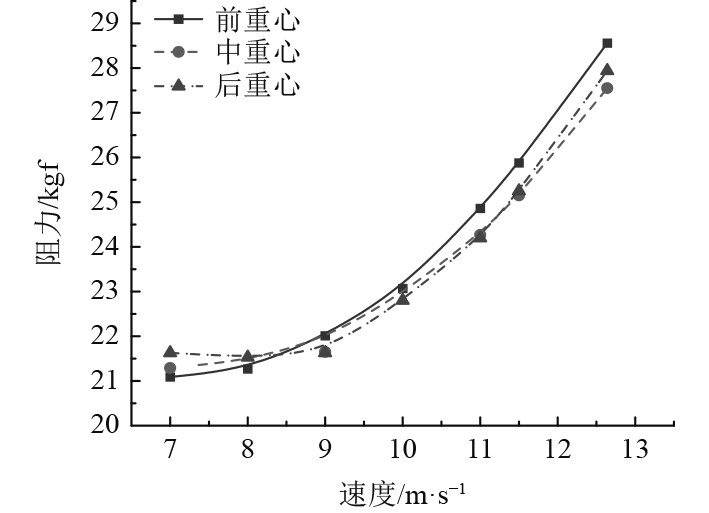
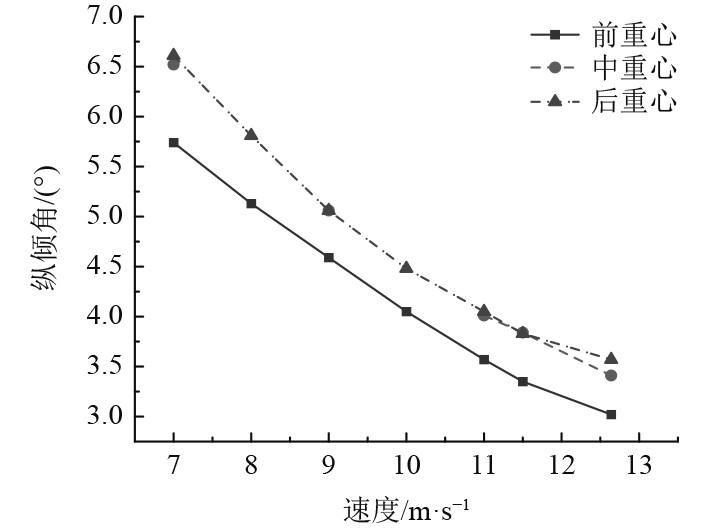
2.1 不同重心位置的阻力性能对比3个不同重心纵向位置的试验工况对比,如图3和图4所示。可以看出,在其他条件均相同时,重心位置在一定范围内越靠近船首,则航行纵倾角越小,导致模型湿表面积越大,滑行效率越低,阻力性能也就越差。
|
图 3 静水阻力试验结果对比 Fig. 3 Comparison of hydrostatic resistance experiment results |
|
图 4 纵倾角对比 Fig. 4 Comparison of trim angle experiment results |
初始后重心与中重心的状态下,阻力与模型纵倾角及阻力相差均较小。考虑到选择最优阻力性能的状态进行水动力试验,后续敲击试验的模型重心位置均选择为中重心。
2.2 不同冲量的敲击试验结果对比在零速状态下开展变冲量的敲击试验,对比不同冲量对巡逻艇模型的横向稳定性影响,结果如表3所示。
|
|
表 3 不同冲量的敲击试验结果 Tab.3 Percussive experiment results of different impulse |
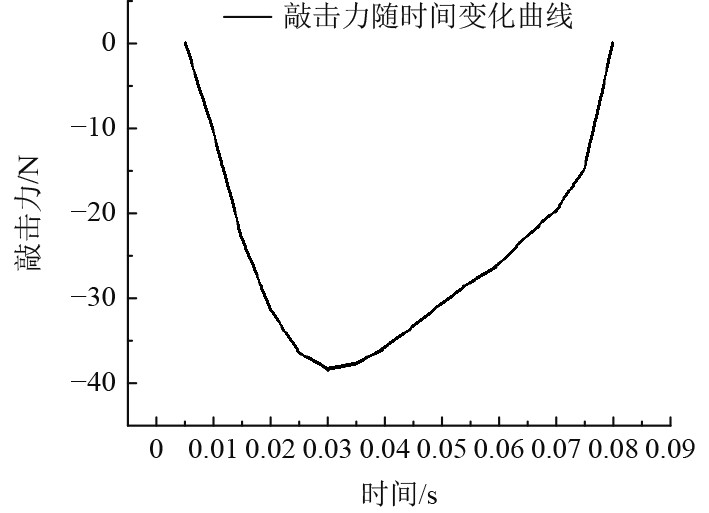
|
图 5 工况4的敲击力时历曲线 Fig. 5 The percussive force time-history curve of GK4 |
从表3的试验结果可以看出,模型横倾角与外力的冲量大小呈正相关变化,但并不是简单的线性关系。从工况2与工况3的结果对比可以看出,当冲量在较小的量级上增加时,横倾角的变化率较大,而当外力带到一定数值时,最大横倾角的增量将会变小,这与船体模型本身的横向恢复力矩增加存在很大关系。
冲量为1.9 N·s的敲击力与横倾角变化曲线如图6所示。可以看出,在零速横摇状态,模型从最大横倾角恢复至平衡位置的过程很缓慢,即横摇衰减系数较小。
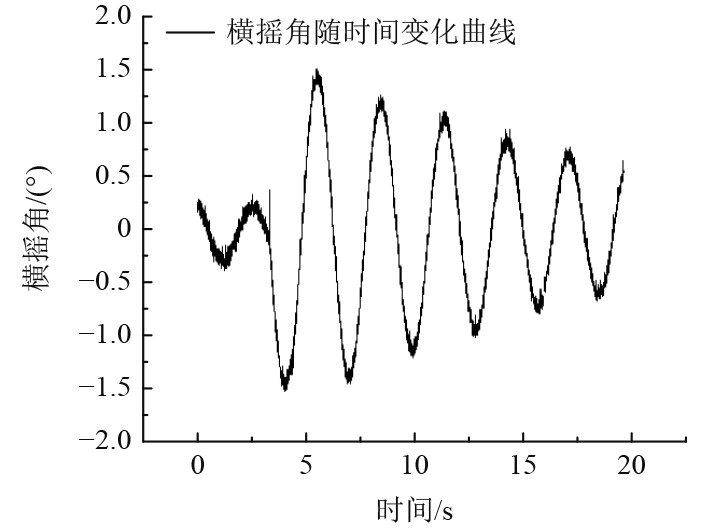
|
图 6 工况4的横倾角变化时历曲线 Fig. 6 The roll angle time-history curve of GK4 |
为研究重心高度对横向稳定性的影响,将模型重心位置进行调整,开展工况4与工况7的对比试验。
图7为工况7的横摇衰减曲线。可以看出,随着重心的升高,模型的最大横倾角增大为1.8°。这表明降低重心高度对模型的横向稳定性具有积极的作用,在巡逻艇火炮系统的安装方面应该注意其安装高度。
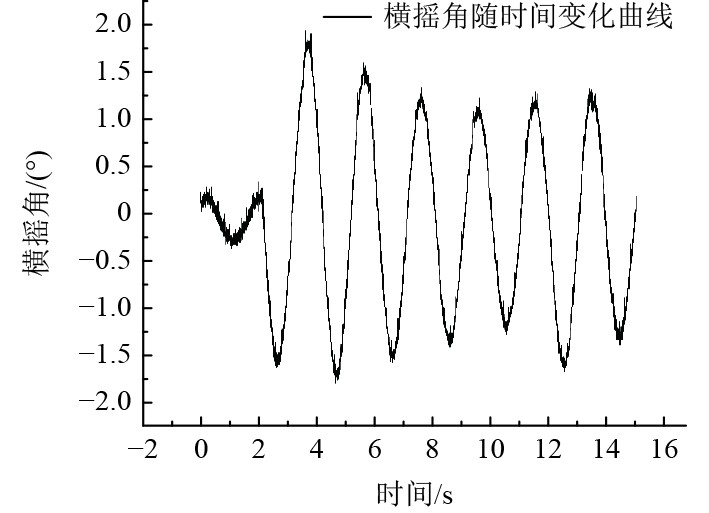
|
图 7 工况7的横倾角变化时历曲线 Fig. 7 The roll angle time-history curve of GK7 |
巡逻艇的火炮系统一般是在巡逻执法过程中使用,艇速较快。因此,开展航速变化对火炮后坐力导致的横向失稳影响规律研究至关重要。
选取中、高速状态进行敲击试验,开展工况8~工况11的试验,通过对比不同速度的最大横倾角,研究航速对横向运动稳定性的影响规律。
图8为不同航速状态下的模型最大横倾角变化曲线。可以看出,尽管受到的外力冲击相同,但航速的不同导致巡逻艇模型的最大横倾角存在一定的差异,尤其是零速状态和带航速状态,最大横倾角存在较大的差异。当航速增大到一定程度时,速度的增加对最大横倾角的影响开始变得较小。这是因为当巡逻艇以一定的航速进行滑行时,艇体两侧会提供较大的水动升力,当受到火炮后坐力冲击时,水动升力能够起到一定的抵消作用。
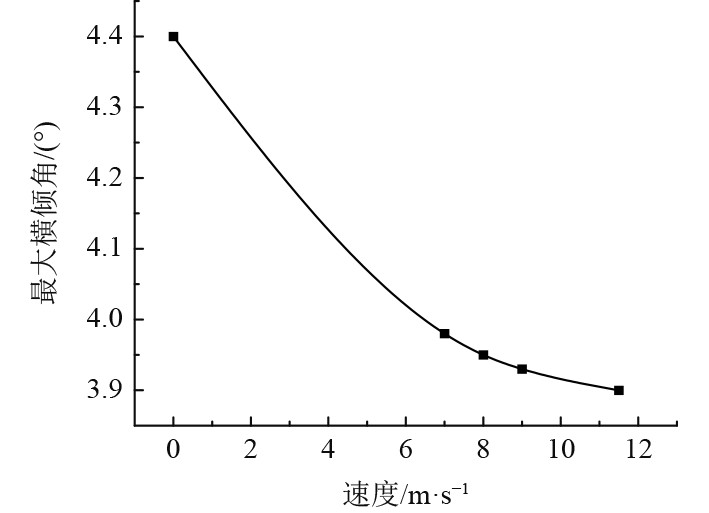
|
图 8 不同航速的最大横倾角变化曲线 Fig. 8 Maximum roll angle at different speed |
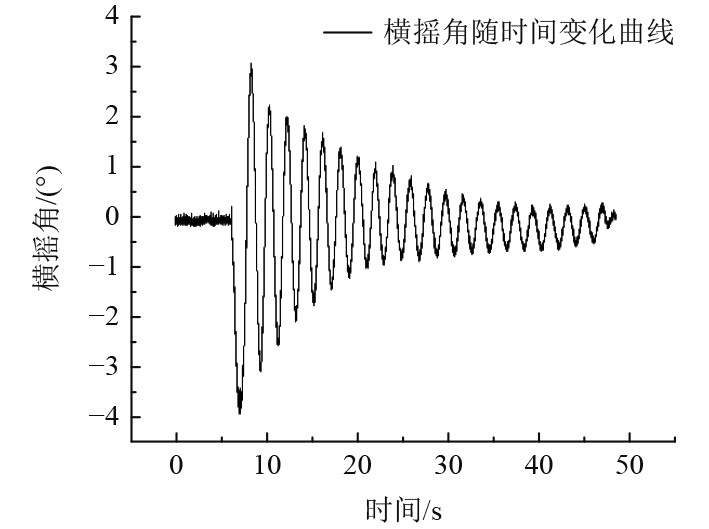
|
图 9 工况11的横倾角变化时历曲线 Fig. 9 The roll angle time-history curve of GK11 |
针对高速执法巡逻艇因火炮射击后坐力而导致的横向失稳问题,本文采用基于模型试验的方法,对高速艇在航行中受外力冲击的运动横稳性进行缩比模型试验,就重心纵向位置、重心高度、冲量及航速大小等4大因素对高速艇航行稳定性的影响规律开展试验研究,得出主要结论如下:
1)在一定范围内,重心位置越靠近船首,模型的航行纵倾角越小,滑行效率越低,阻力性能越差。
2)零速状态下,外力冲量在较小的量级变化时,最大横倾角随冲量的变化率更大。
3)巡逻艇模型的重心高度对其横向稳定性的影响较大,巡逻艇应尽量控制其火炮系统的安装高度。
4)航速对巡逻艇模型的运动横稳性具有明显的影响,艇体模型在带航速状态比零速状态更耐冲击,但随着航速增大,这种影响也会逐渐变小。
| [1] |
IMO. SDC1/INF. 8 Annex 27 draft guidelines of direct stability assessment procedures as a part of the second generation intact stability criteria[S]. London: IMO, 2014.
|
| [2] |
杨春蕾, 朱仁川, 缪国平, 等. 一种基于计算流体力学的三维船舶横摇阻尼预报方法[J]. 上海交通大学学报, 2012(8): 1190-1195. DOI:10.16183/j.cnki.jsjtu.2012.08.004 |
| [3] |
MANCINI S, BEGOVIC E, PIZZIRUSSO D, et al. Roll damping assessment of intact and damaged ship by CFD and EFD methods[C]//Proceedings of Ships and Ocean Vehicles. Glasgow: University of the Strathclyde, 2015: 501–211.
|
| [4] |
GU M, Lu J. Numerical simulation of the ship roll damping [C]//Proceedings of Ships and Ocean Vehicles. Glasgow: University of the Strathclyde, 2015: 341–348.
|
| [5] |
王硕. 滑行艇高速航行稳定性能数值与试验研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
| [6] |
约翰D. 安德森. 吴颂平, 刘赵淼, 译. 计算流体力学基础及其应用[M]. 北京: 机械工业出版社, 2007.
|
| [7] |
王硕, 苏玉民, 庞永杰, 等. 高速滑行艇CFD精度研究[J]. 船舶力学. 2013, 17(10): 1107–1114.
|
 2023, Vol. 45
2023, Vol. 45
