随着海上“丝绸之路”的不断建设,我国进出港船舶数量与日俱增,各个港口引航需求逐步提升。性能优良的引航船是引航交接工作过程中不可或缺的重要交通装备,所以对其船型及阻力性能的研究具有一定的实际意义和应用价值。
通常,高速引航交通船船型大多为V型。对于其折角线长度对性能的影响已经有了一系列探究[1-2],包括与折角线形状相关的船底斜升角大小、船首折角线高度等参数给出了使用范围[3-4],但还不够细致。本文在某V型的基础上,针对折角船型的折角线形状,通过选取较敏感的参数进行更加深入、更加系统的研究,对折角船型的研究做出有益的补充,同时为折角线的设计把控提供一些参考。
1 船型设计 1.1 基本船型概述 1.1.1 基本船型主要参数选取某高速引航V型艇作为基本船型,采用双喷水推进器,设计航速为28 kn。其主要参数如表1所示。
|
|
表 1 某高速引航V型艇主要参数 Tab.1 Main parameters of a high-speed pilot V-boat |
基本船型为单折角线、前倾首与垂直尾型线,其折角线最大宽度为0.9B(距船首垂线40 %L);尾封板处宽度与折角线最大宽度的比值为0.8;折角线与水线交点距首垂线1/3 L,与首柱交点高为1.5 m;中部斜升角为18°,尾部逐渐减小。
1.2 系列船型方案设计V型艇的折角线是一条复杂的三维曲线,它的形状及参数关联着船型几何形状及其性能。本文以阻力性能为考量,在不改变船舶的主要船体参数及排水体积的原则下,通过折角线参数的进一步分析与改变,生成系列船型方案。
1.2.1 折角线参数的选择根据文献[5],确定船首垂线与折角线交点A、设计水线与折角线交点B、折角线最大宽度点C、尾封板与折角线交点D为折角线的控制点。考虑到

|
图 1 折角线参数示意图 Fig. 1 Schematic diagram of the corner line parameters |
通过改变其在X、Y、Z方向上的参数值就可以相对便捷地控制折角线的整体形状。
1.2.2 生成系列船型方案根据文献[6]可知,设计水线与折角线交点距首垂线为(1/3~1/4)L;折角线最宽处横剖面距首垂线(30%~50%)L、最宽值为(0.68~0.97)B;尾封板处折角线宽度为(0.65~0.8)倍的折角线最大宽度。据此,通过各参数选取初始值和终值,同时设置一定步长,再利用排水体积不变的衡准条件,可优选出表2所示的5个系列折角线船型方案。以方案1为例,引航船船型型线如图2所示。
|
|
表 2 系列方案折角线参数 Tab.2 Series scheme folding line parameters |
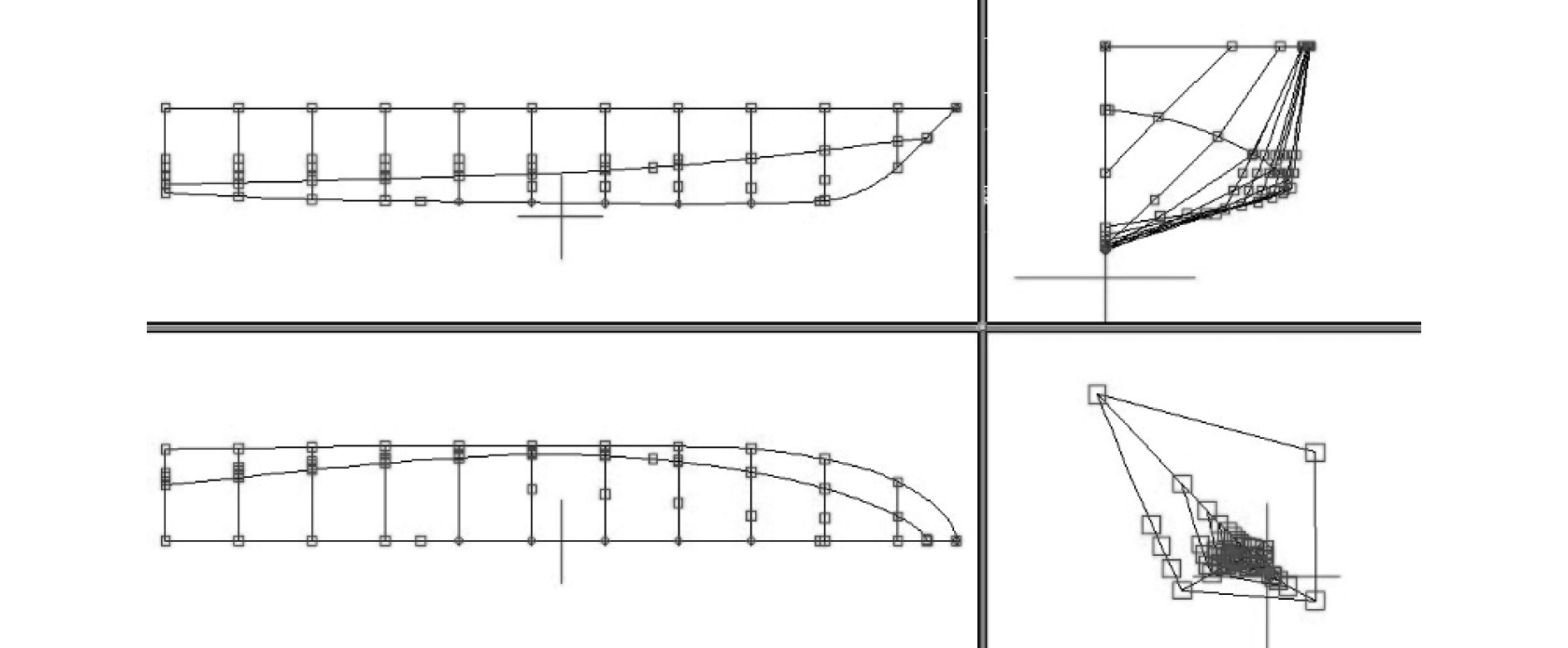
|
图 2 方案1型线示意图 Fig. 2 Scheme 1 type line schematic diagram |
利用文献[6]中的无断级滑行艇阻力的回归公式计算某V型艇1∶10缩放船模在排水体积傅汝德数分别为2和3时的裸船体阻力。艇体计算所需相关形状参数如表3所示。
|
|
表 3 艇体相关形状参数 Tab.3 Hull-related shape parameters |
当
基本船型所有参数均符合回归公式要求,计算4个独立变量如下:
| $\begin{aligned} &{x}_{1}=\frac{{A}_{P}/{\nabla }^{2/3}-6.875}{2.625},{x}_{2}=\frac{100\left(LCG/{L}_{P}\right)-37.15}{7.15},\\&{x}_{3}=\frac{{L}_{P}/{B}_{Pa}-4.54}{2.18},{x}_{4}=\frac{{\beta }_{m}-25.2}{12.2}。\end{aligned} $ |
算得x1 = −0.154 286;x2 = 0.495 1;x3 = −0.341 743;x4 = −0.59。
查文献[5]计算
基本船型船体模型排水量只有28.2 t,小于模型艇的排水量45 t,所以需进行雷诺数修正。首先计算缩尺比与基本船型雷诺数,计算结果如下:
| $ \lambda =\sqrt[3]{\frac{{\mathrm{\Delta }}_{s}}{{\mathrm{\Delta }}_{m}}\cdot \frac{{\rho }_{m}}{{\rho }_{s}}}=0.086 ,$ |
| $ {L}_{Pm}={L}_{P}/\lambda =20.8\;{\rm{m}} ,$ |
| $ {l}_{m}=\frac{l}{{L}_{P}}\cdot {L}_{Pm}=16.225\;{\rm{m}} ,$ |
| $ {l}_{s}=\frac{l}{{L}_{P}}\cdot {L}_{P}=1.3954\;{\rm{m}} ,$ |
| $ {Re}_{m}=\frac{5.885\cdot {Fn}_{\nabla }\cdot {l}_{m}}{1.190\;7\times {10}^{-6}}=1.6\times {10}^{8} ,$ |
| $ {Re}_{s}=\frac{\sqrt{g\cdot {\nabla }^{1/3}}\cdot {Fn}_{\nabla }\cdot {l}_{s}}{1.141\;3\times {10}^{-6}}=0.42\times {10}^{8}。$ |
摩擦阻力系数使用第八届ITTC公式:
| $ {C}_{F}=\frac{0.075}{{\left({\rm{lg}}Re-2\right)}^{2}} 。$ |
计算基本船型的
| $ \frac{R}{\Delta }={\left(\frac{R}{\Delta }\right)}_{45t}+\left({\left({C}_{F}+{C}_{a}\right)}_{s}-{\left({C}_{F}\right)}_{m}\right)\cdot \frac{1}{2}\left(\frac{S}{{\nabla }^{\frac{2}{3}}}\right){Fn}_{\nabla }^{2}=0.138\;7 。$ |
经估算,该船型船模阻力在
在文献[6]中,此方法算例计算结果与船模试验值曲线形态基本吻合,但在中高速段偏高。其中,
当
建立计算域,将1∶10缩放的船体模型导入STAR-CCM+,根据船模主尺度建立试验水池计算域HULL。选取计算域坐标点为角1:[−5L,−2L,−2L];角2:[2L,2L,1L]。计算域设置情况如图3所示。
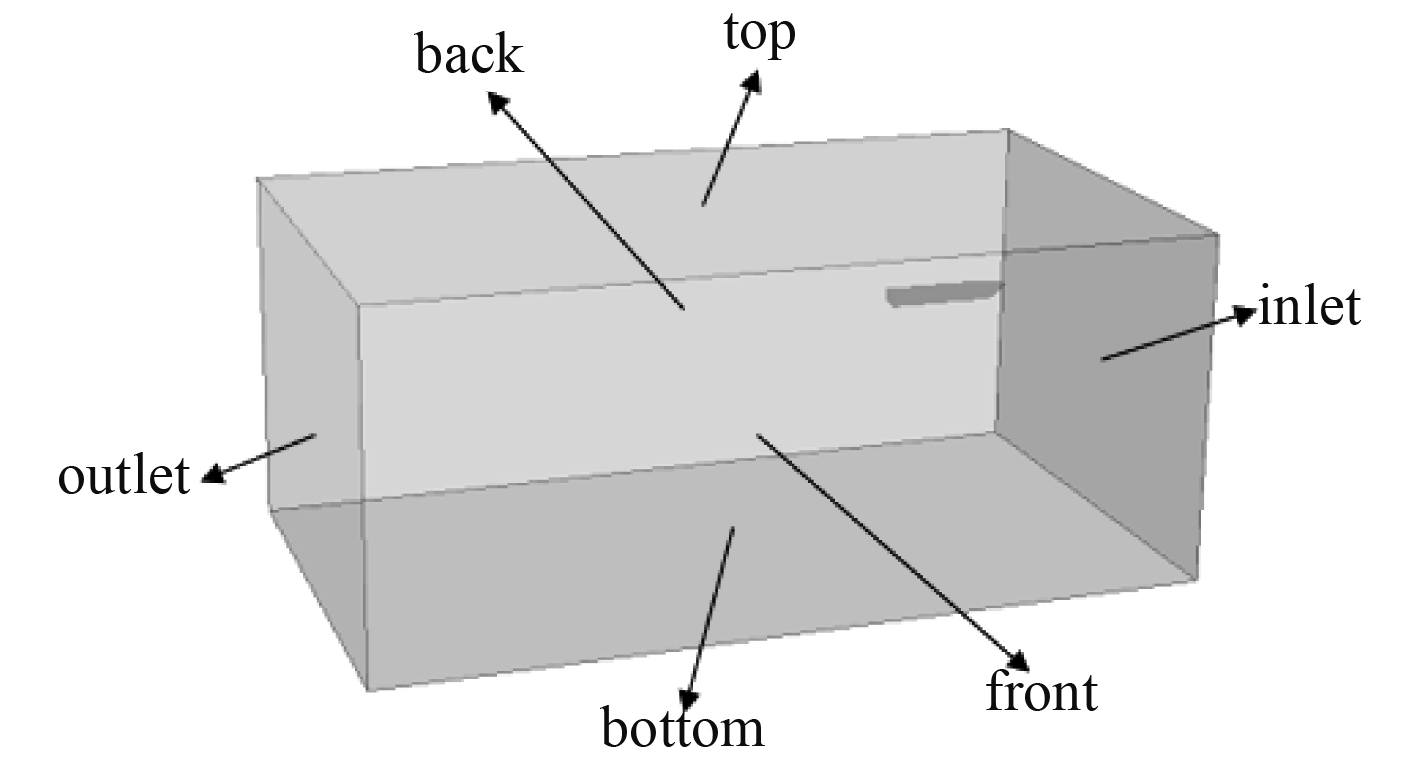
|
图 3 船模计算域 Fig. 3 Ship model computational domain |
运用重叠网格方法,建立刚好能包裹住船体的长方体计算域overset,使其与船体模型进行减运算,作为重叠网格区域,如图4所示。另外将船首、船后流场与自由液面处进行适当加密,如图5所示。
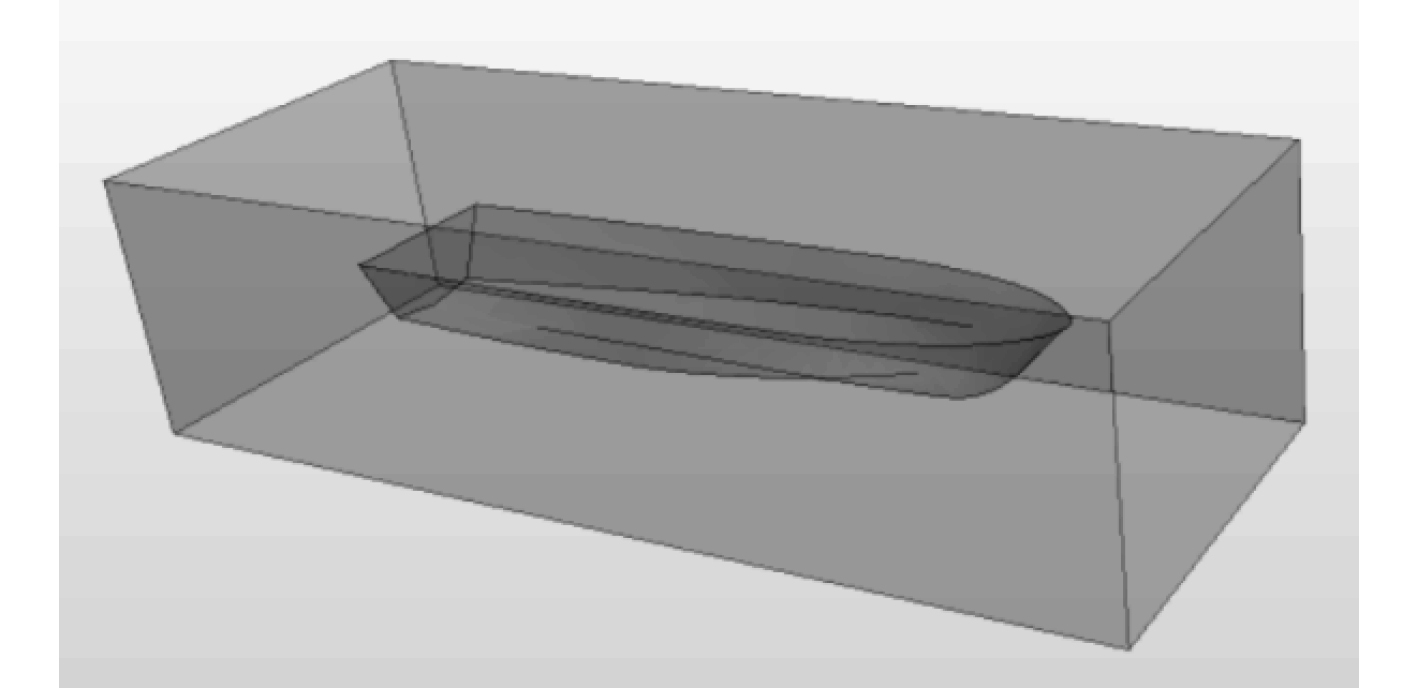
|
图 4 Overset区域 Fig. 4 Overset area |
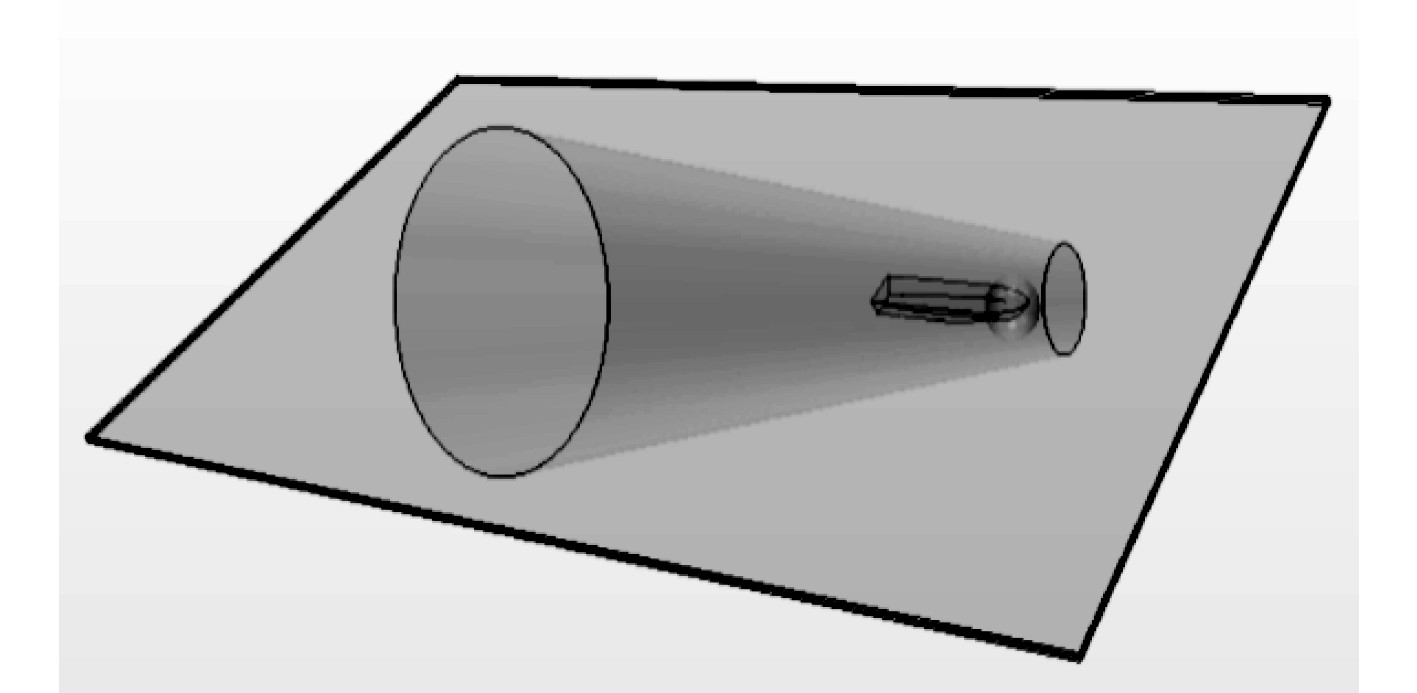
|
图 5 加密区域 Fig. 5 Encrypted area |
分别为HULL与减运算新建自动网格,选取表面重构、自动表面修复、切割体网格单元生成器及棱柱层网格生成器并设置各项参数。网格参数的选取决定了网格的质量,各个参数间有一定的比例关系,需根据效果不断调整,本研究选取网格基础尺寸0.15 m,棱柱层层数为6,计算域HULL的网格需要添加6个面及水线面处的自定义控制,而减运算网格需添加船体表面的加密控制。通过网格的无关性验证,最终确定网格数约为83万。网格划分结果如图6所示。
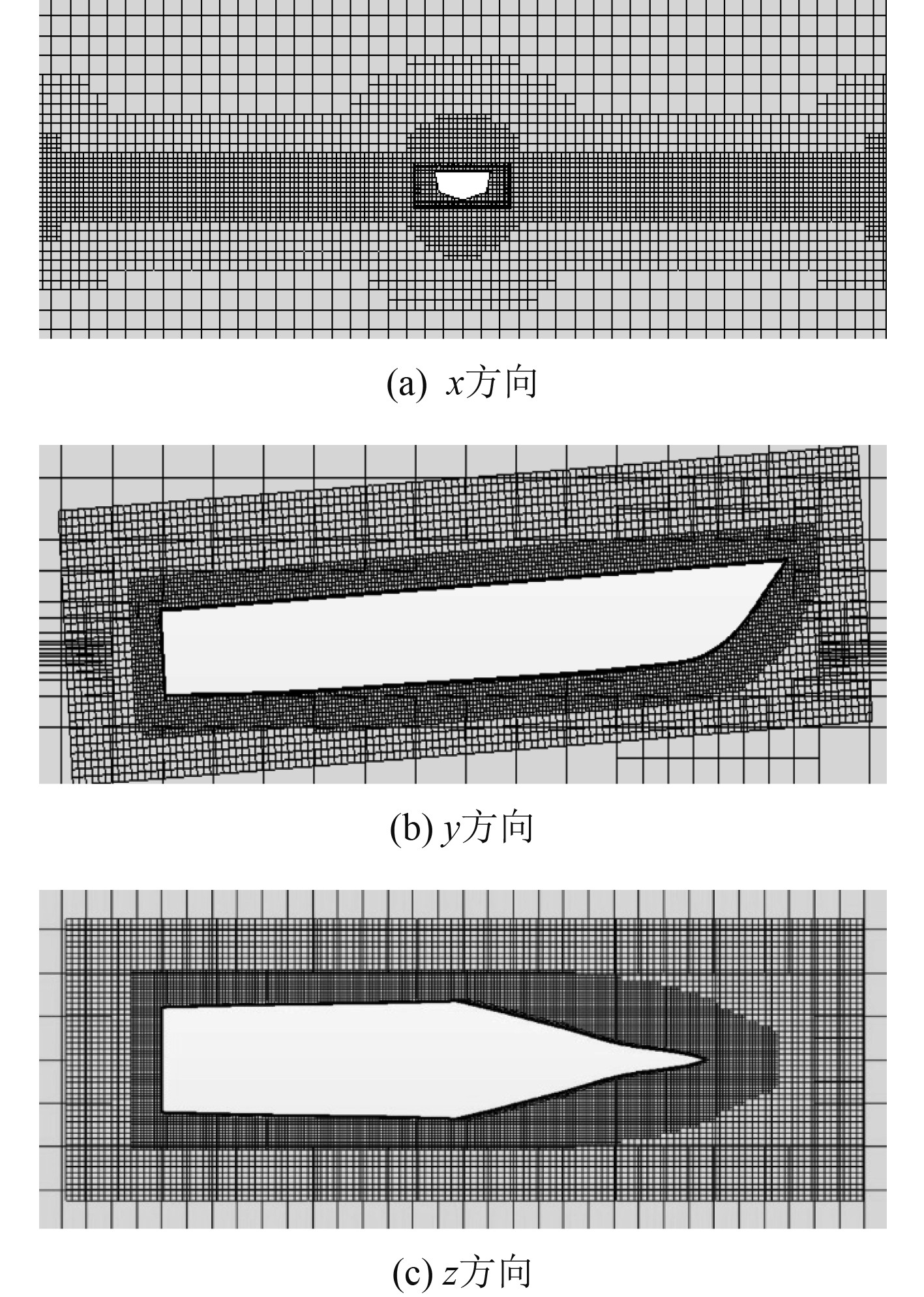
|
图 6 网格划分结果 Fig. 6 Meshing results |
新建物理连续体,选用三维隐式不定常求解器、欧拉多相流模型、SST
设置报告和绘图,建立船行波场景,时间步设置为0.01 s,最大内部迭代为10。
2.4 仿真方法验证在静水、航速21.6 kn(Fr▽=2)的工况下,船模速度为3.513 6 m/s,基本船型阻力仿真计算结果如图7所示。可以看出,船模阻力值逐渐稳定至32.7 N,与理论计算值相差6.7%;当航速为31.8 kn(Fr▽=3)时,船模速度为5.172 8 m/s,仿真方法同上,仿真结果为37.3 N,误差为1.1%。对仿真结果和理论计算结果进行比较,产生的误差在可接受范围内,证明了此数值仿真方法的可靠性。
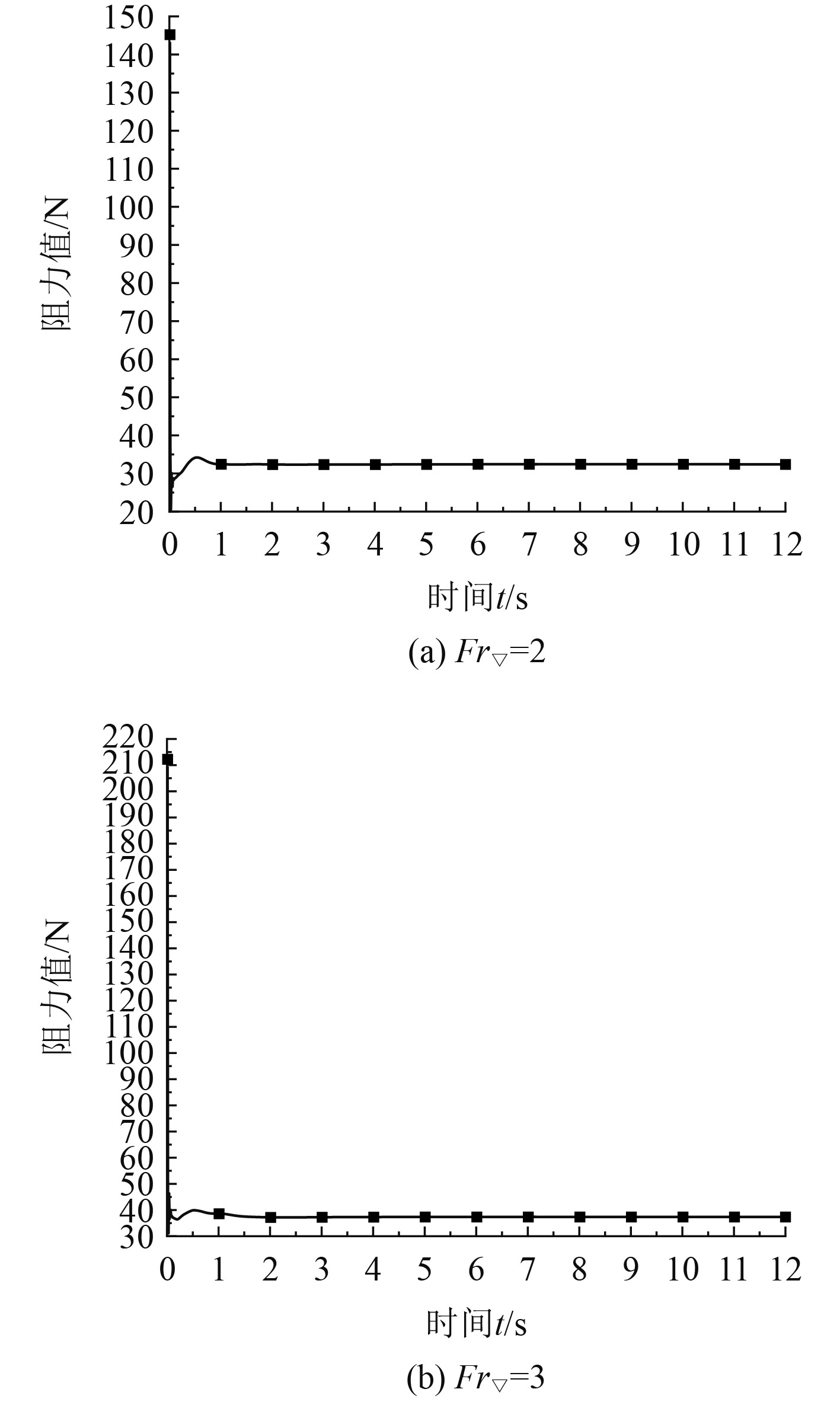
|
图 7 阻力仿真结果 Fig. 7 Resistance simulation results |
运用上述阻力数值仿真方法对基本船型和系列船型的阻力分别在20 kn(Fr▽=1.88)、24 kn(Fr▽=2.26)、28 kn(Fr▽=2.9)、32 kn(Fr▽=3.32)下进行数值仿真计算,阻力仿真结果见表4,阻力变化趋势如图8所示。
|
|
表 4 静水阻力仿真结果 Tab.4 Hydrostatic resistance simulation results |
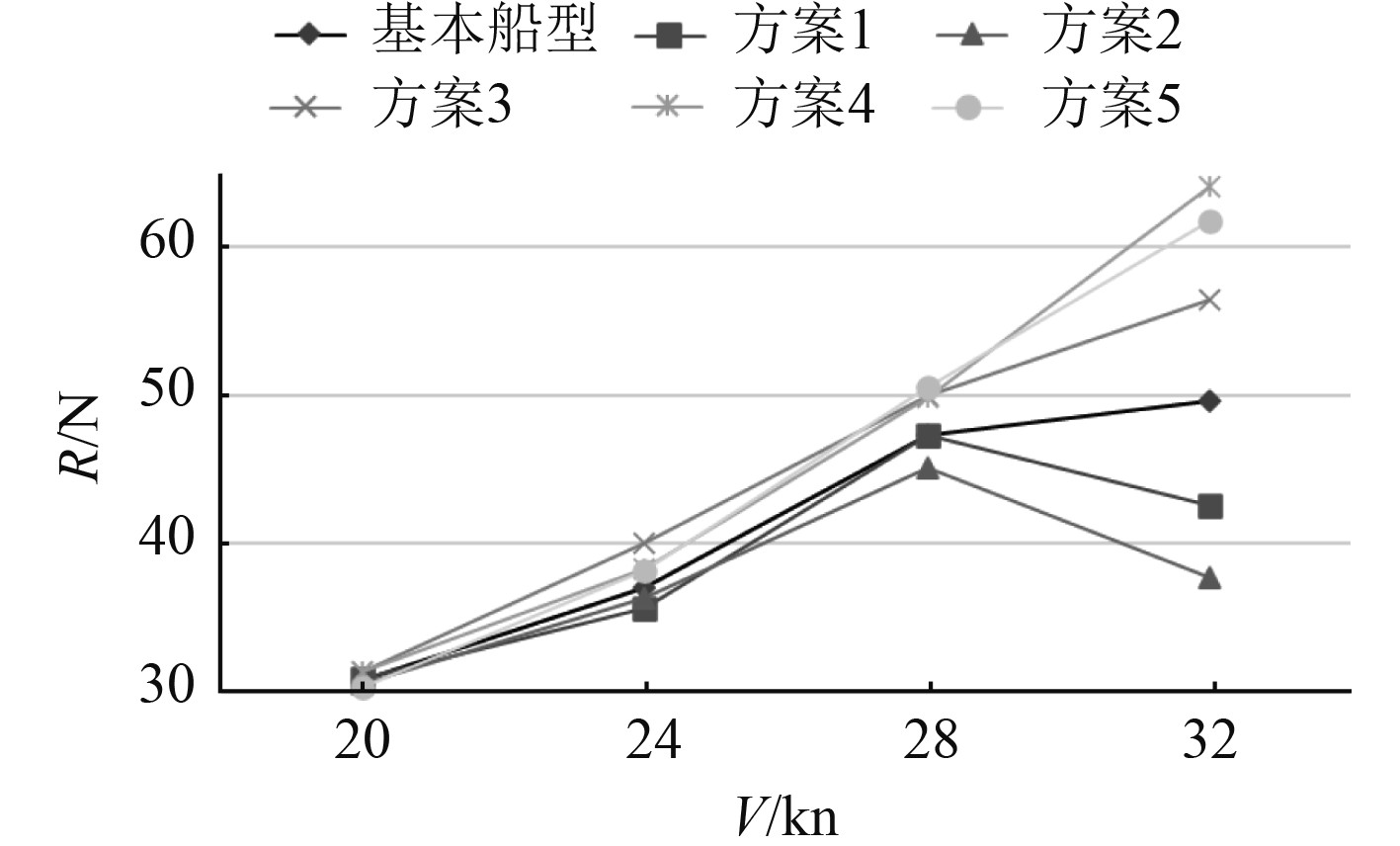
|
图 8 阻力仿真结果对比图 Fig. 8 Comparison of resistance simulation results |
可知,包括基本船型在内的6个船型方案,其静水阻力基本随速度提高而变大,但对于方案1和方案2,航速达到28 kn后,其阻力有减小趋势。
在以上方案中,方案2静水阻力性能最优,在航速32 kn时的阻力值比基本船型同速的阻力值下降20%以上;而方案3阻力性能相对较差,在航速28 kn时的阻力较基本船型增大10%以上。究其原因,可能是折角线最大宽度及其位置距船尾的距离对航行姿态有较大的影响。
4 结 语在某引航高速船V型船的基础上,分析折角线相关参数及变化范围,从而生成了折角线形状不同的系列船型方案,并进行了阻力数值仿真分析与计算。得到以下结论:1)方案2体现了较优越的阻力性能。2)折角线与设计水线交点距船尾的距离XB、折角线最大宽度YC及其位置距船尾的距离XC对其阻力性能有较大影响。考虑到数值仿真方法的局限性,上述结论还有待通过实船试验对其进一步研究。
| [1] |
彭言峰. 排水型圆舭折角高速船阻力数值仿真及其计算方法研究[D]. 镇江: 江苏科技大学, 2015.
|
| [2] |
谢云平, 姚诚钰, 姚伟. 圆舭折角高速船型线参数化设计及其阻力性能分析[J]. 船舶工程, 2012, 34(4): 21-23+40. DOI:10.13788/j.cnki.cbgc.2012.04.013 |
| [3] |
姚朝帮, 董文才, 许勇, 等. 深V型艇系列模型纵向运动试验研究[J]. 哈尔滨工程大学学报, 2010, 31(9): 1138-1143. DOI:10.3969/j.issn.1006-7043.2010.09.002 |
| [4] |
朱云翔. 基于Savitsky法滑行艇航行姿态参数影响研究[J]. 海洋工程, 2021, 39(1): 162-170. DOI:10.16483/j.issn.1005-9865.2021.01.017 |
| [5] |
岳国强, 姚朝帮, 董文才. 深V型滑行艇静水阻力性能影响因素研究[J]. 中国舰船研究, 2009, 4(3): 24-27+37. DOI:10.3969/j.issn.1673-3185.2009.03.005 |
| [6] |
朱珉虎. 《高速艇与游艇设计手册》[J]. 船舶, 2014, 25(1): 38. DOI:10.19423/j.cnki.31-1561/u.2014.01.007 |
 2023, Vol. 45
2023, Vol. 45
