0 引　言

在现代海战中，鱼雷作为传统装备占据着举足轻重的地位^[1]。随着反潜技术的快速发展，一连串高新技术相继被应用于鱼雷上，鱼雷的杀伤力和攻击范围也在不断增强，使得鱼雷防御成为舰艇安全的必要任务^[2-3]。

按驱动方式，鱼雷分为线导、火箭助飞和空投。对于舰艇而言，对来袭鱼雷轨迹的判断是有效规避或实施防御性策略的一个重要依据^[4]。通过研究和仿真来袭鱼雷的轨迹，可有效判断来袭鱼雷的类型，为准确制定对抗鱼雷的方法提供依据。若能在鱼雷报警后尽早判别出其类别，可更早采取措施，进而提高舰艇的生存概率。

从现有研究来看，关于鱼雷制导轨迹判别的文献较少。陈颜辉等^[5]总结了13个指标来识别鱼雷的制导方式，但其中缺乏鱼雷的方位信息。余跃等^[6]分析了鱼雷开始自导前直线航行段的方位变化率，但不同制导方式鱼雷间的方位变化率差异过小，无法满足实际中的识别误差。尹文进等^[7]针对方位条件下的来袭鱼雷弹道预测问题，提出一种通过声呐系统探测的鱼雷方位信息，分为直航鱼雷、尾流自导鱼雷、潜射线导鱼雷进行运动要素合理性判别，反推计算出来袭鱼雷的运动要素，即估计速度、估计和解算运动航向的集合。但此方法含多个区间分析，在剔除不合理的鱼雷运动航线的同时容易将合理值一并漏去。针对以上问题，本文提出一种基于长短期记忆网络的鱼雷轨迹分类方法，实现对来袭鱼雷类型的预测。

1 鱼雷预测模型 1.1 潜射线导鱼雷航向预测模型

线导鱼雷攻击是舰艇对水面目标远距离攻击的主要方式之一^[8]。理论上讲，只要有目标方位信息就可以实施线导鱼雷攻击^[9]。采用线导导引可扩大鱼雷的攻击范围，攻击速度快，因此国内外远航程鱼雷大都采用线导导引^[10-11]。

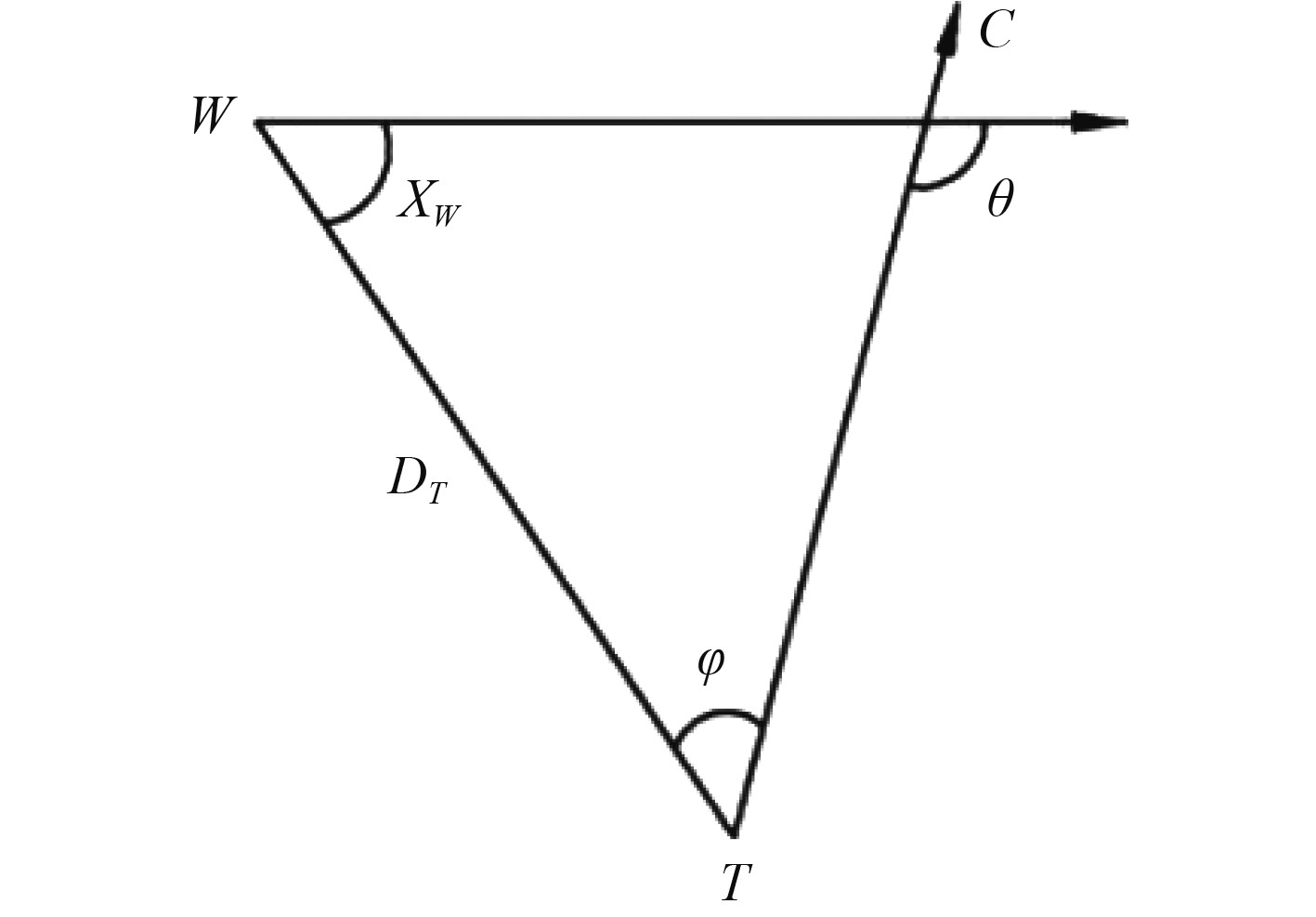
已知目标运动特征，目标舰艇W在等速直航条件下可以根据三角函数求解发射提前角^[12]，如图1中的 $ \Delta CTW $ ，进攻方T根据所求的提前角 $ \varphi$ 发射直航雷，在命中点C处，鱼雷与舰艇交汇。

假设鱼雷来袭报警时刻，舰艇位于W点，速度为V_W且沿WC方向直航。设鱼雷速度V_T，报警舷角X_W，可根据舰艇位置W、鱼雷出射位置T和命中点C，依据三角函数得到下面的关系式^[13-14]：

$ \frac{\sin \varphi}{V_{W}}=\frac{\sin X_{W}}{V_{T}}，$

(1)

整理得到鱼雷出射提前角为：

$ \varphi={\rm{arcsin}}\left(\frac{V_{W} \sin X_{W}}{V_{T}}\right)。$

(2)

式中仅有 $ V_{T} $ 为未知量。如能获取 $ V_{T} $ 的估计值，就能计算出提前角，确定线导鱼雷航向。

1.2 火箭助飞鱼雷航向预测模型

火箭助飞鱼雷由舰艇发射，经火箭空中助飞到预定点入水，然后自动搜索、跟踪和攻击舰艇^[15]。鱼雷射出后先沿直线在空中航行，入水后其上挂载的探测设备在水下搜索并发现目标，测得相关运动要素后，由射击指挥系统自动给鱼雷设定航深、航速、波束宽度等参数，进行自导打击目标任务。

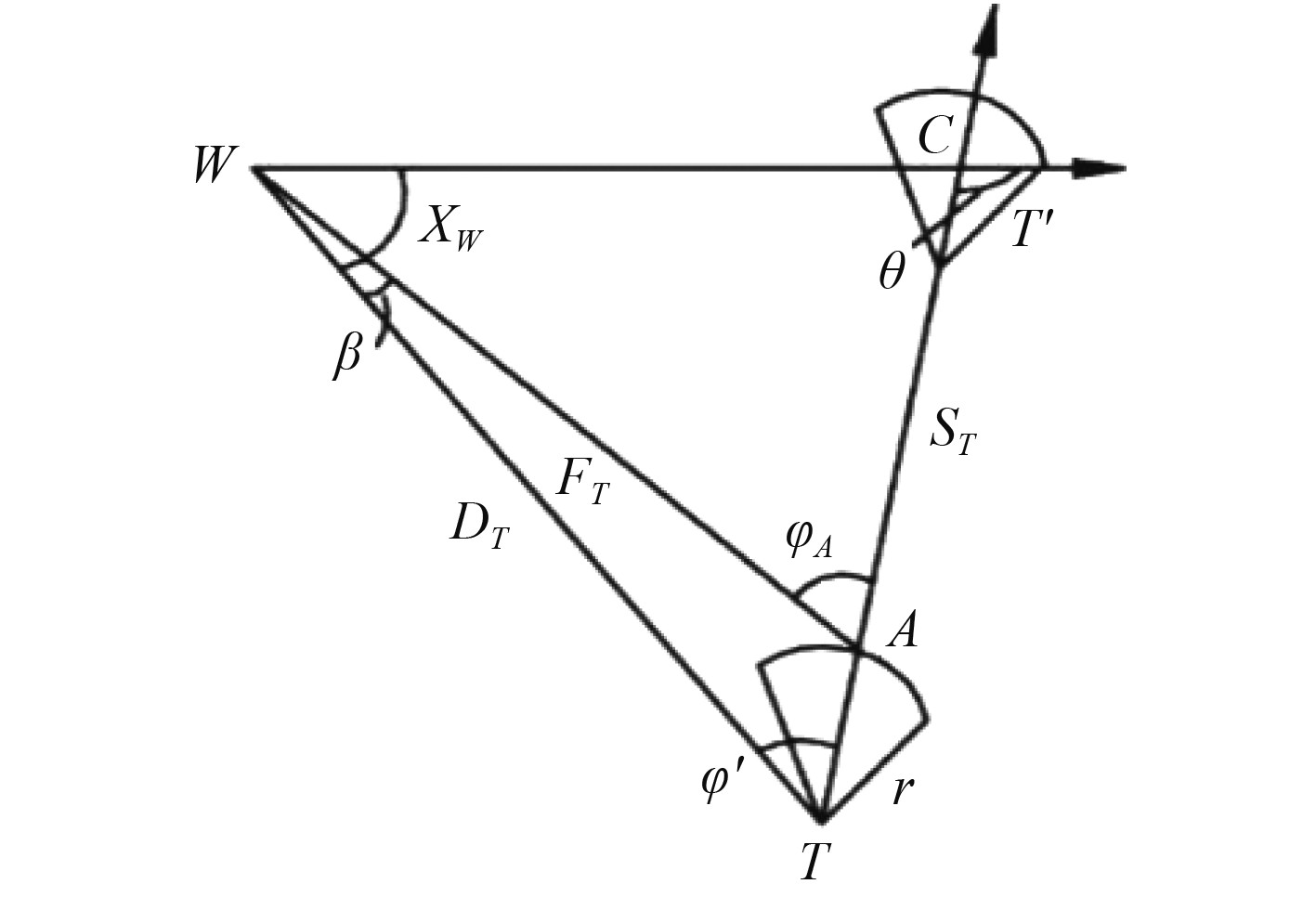
如图2所示，当鱼雷的自导扇面中点A与打击目标构成三角形 $ \Delta CAM$ 时，鱼雷命中率最高^[14]，与其对应的 $ \varphi '$ 称为有利提前角。

由图2中的 $ \Delta CAM$ ，推导出火箭助飞鱼雷搜索段的有利提前角为^[13-14]：

$ \varphi '={\rm{arcsin}}\left(\frac{D_{T} \sin \beta}{r}\right)-\beta。$

(3)

其中：

$ \beta={\rm{arctan}} \left[\frac{\sin X_{W}}{\dfrac{D_{T} V_{T}}{\left(r V_{w}\right)}+\cos X_{W}}\right] 。$

(4)

式 中： $ V_{W} $ ， $X_W $ 为检测值； $ V_{T} $ ， $ D_T $ ，r为估计值。只要确定这5个变量就能得到有利提前角 $ \varphi '$ ，进而预测出攻击轨迹^[16]。

1.3 空投鱼雷航向预测模型

空投鱼雷，又称航空鱼雷，是航空反潜的主要武器^[17]，其最大优势是可以弥补鱼雷本身航程短和航速低的不足。当载机接收到探测平台发送的目标信息时，火控系统将利用此信息计算出合适的鱼雷投放参数。鱼雷经降落伞降入水后，便会跟随目标舰艇的尾流进行制导^[18]。

相比于火箭助飞鱼雷，空投鱼雷在水下的自导原理类似，其方法是在目标的有效尾流中某点建立三角形。有效尾流一般选取在尾流中点附近^[19]。实际海况下，有效尾流的长度存在较大波动，可通过如下公式计算^[20]：

$ L=\left\{\begin{split}&180V_W\text{，}3级海况，\\ &120V_W\text{，}4-5级海况。\end{split} \right. $

(5)

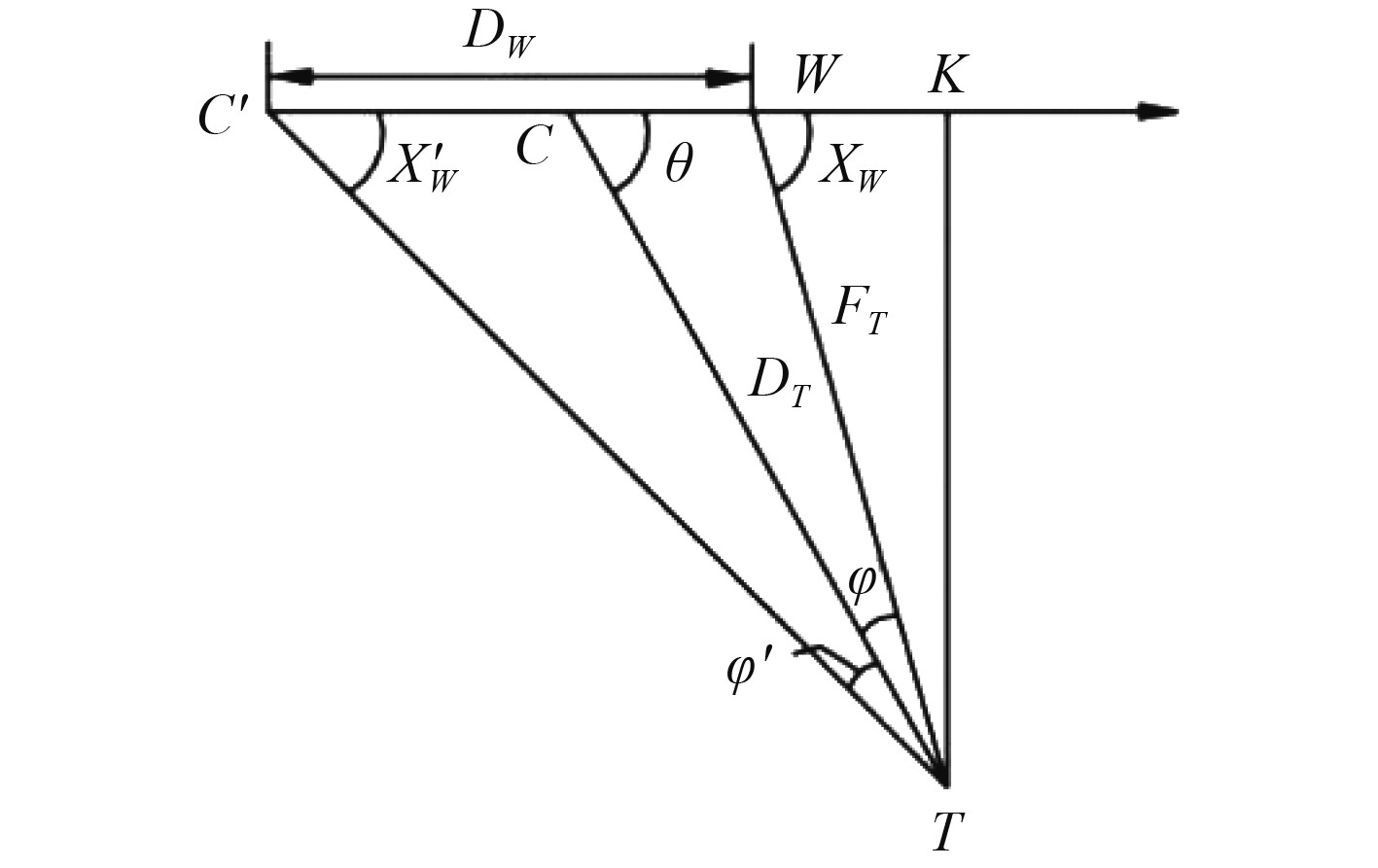
如图3所示，设舰艇以V_W速度沿WC方向航行，航行至W点时报警鱼雷来袭，报警舷角为X_W，鱼雷从T点射出，沿TC。设期望打击位置C'到舰艇尾部的距离为D_W，从T向CW做垂线交于点K，通过 $ \Delta CTK$ 得出：

$ X_{W}'={\rm{arctan}} \left[\frac{D_{T} \sin \left(X_{W}\right)}{D_{W}+D_{T} \cos \left(X_{W}\right)}\right] ，$

(6)

鱼雷射击提前角为：

$ \varphi=X_{W}-X_{W}'-\varphi'，$

(7)

通过 $ \Delta C'TC $ 可得到 $ \varphi'$ 的表达式：

$ \varphi'={\rm{arcsin}}\left\{\frac{V_{W}}{V_{T}} \sin \left[{\rm{arctan}} \left(\frac{D_{T} \sin \left(X_{W}\right)}{D_{W}+D_{T} \cos \left(X_{W}\right)}\right)\right]\right\}。$

(8)

式中： $ V_{W} $ ， $ {X}_{{W}} $ 为检测值； $ {V}_{{T}} $ ， $ {D}_{{T}} $ ，D_W为估计值。只要确定这5个变量就能得到有利提前角 $ \varphi$ ，进而预测出空投鱼雷的攻击轨迹^[16]。

2 仿真方法概述

鱼雷制导仿真可以作为鱼雷类型判断的重要依据。鱼雷的运动轨迹由鱼雷的导引方法和目标运动形式共同决定。经典的鱼雷导引方法包括尾追法、固定提前角法、平行接近法以及可变提前角法等^[21-22]。其中可变提前角导引法受制约的参数较多，对舰载发射设备要求较高，不纳入本文考虑范围，只对前3种方法进行仿真研究。

通过建立各导引方法的模型，对比分析鱼雷运动参数对各方法弹道的影响，研究3种鱼雷经典制导律的导引原理。全弹道指的是鱼雷从发射直到命中目标（或燃料耗尽）的整个运动过程。当鱼雷在水中缺少目标信息的条件下，使用任何导引方法都需满足特定条件，且盲目使用会削弱鱼雷击中目标的概率，故此时不宜直接使用任何导引方法。若已知目标大致方位，鱼雷入水后需通过机动，以产生足够大的目标舷角，扩大鱼雷的搜索范围并增加鱼雷击中目标的能力。

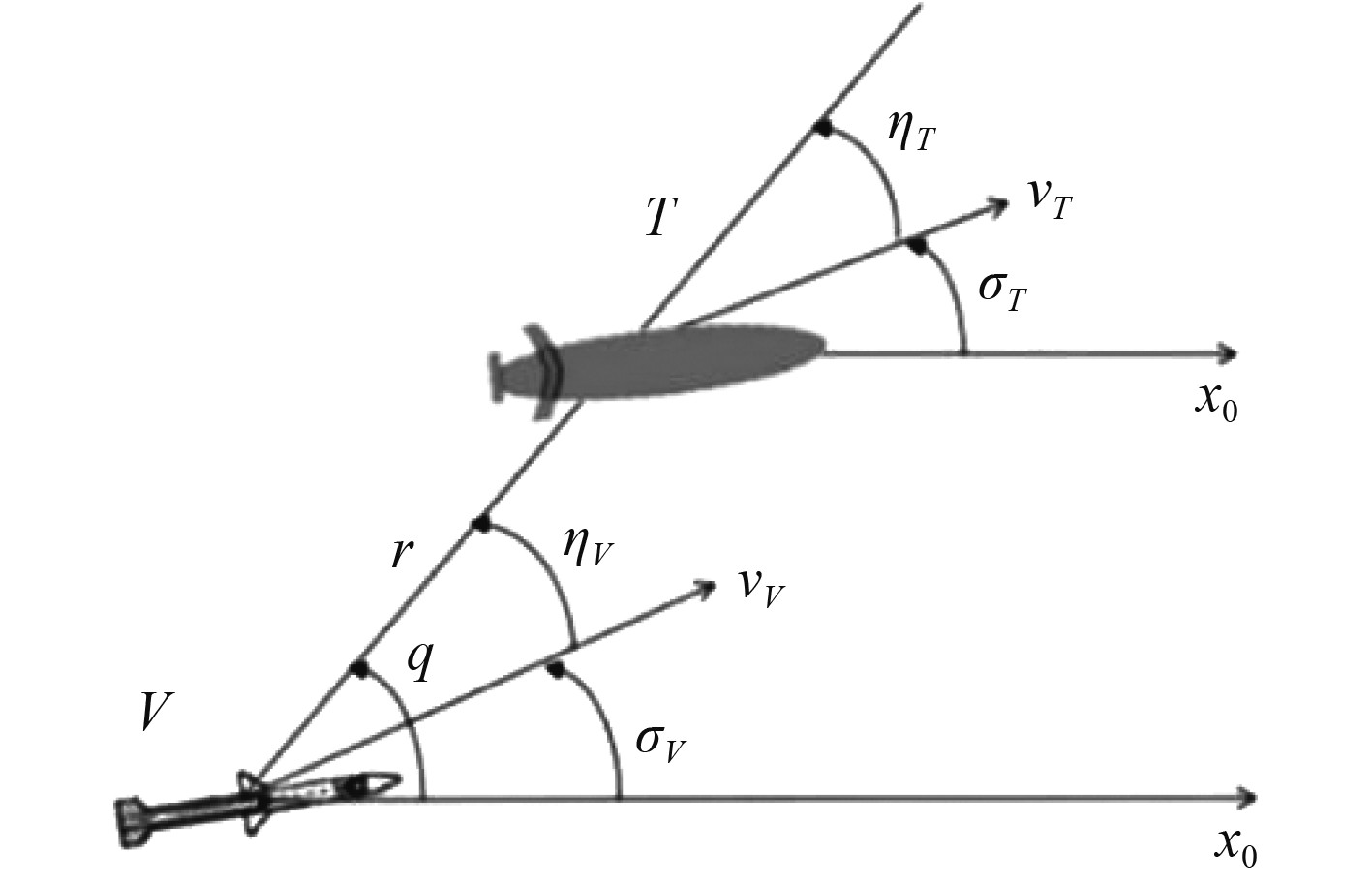
2.1 尾追法

该方法是最早提出的导引方法，指在鱼雷攻击目标的导引过程中，鱼雷的速度矢量始终指向目标。尾追法^[23-24]也被称为直接瞄准导引法，意味着鱼雷的航向角与鱼雷目标视线角的夹角为0。使用这种方导引时，鱼雷的运动方向始终指向目标，并在尾部命中。尾追法的原理模型如图4所示。

鱼雷导引运动时的相对运动方程为：

$ \left\{ \begin{split}& \dfrac{{\rm{d}}r}{{\rm{d}}t}=V_T {\rm{cos}} \eta_T-V_V {\rm{cos}} \eta_v，\\ & \dfrac{{\rm{d}}q}{{\rm{d}}t}=\frac{1}{r}(V_V {\rm{sin}} \eta_V-V_T {\rm{sin}} \eta_T)，\\ &q_v=\sigma_V+\eta_V，\\ &q_t=\sigma_T+\eta_T。\end{split} \right. $

(9)

式中：r为鱼雷与目标位置的相对距离； $ V_{T} $ 为目标的瞄准线；q为目标瞄准线与攻击平面基线的夹角，即目标的方位角； $ \sigma_V$ ， $ \sigma_T$ 分别为鱼雷、目标速度矢量与攻击平面基线之间的夹角，称为鱼雷弹道角和目标航向角； $ \eta_V $ ， $ \eta_T$ 分别为鱼雷、目标速度矢量与目标瞄准线之间的夹角，称为鱼雷速度提前角和目标速度提前角^[23-24]。此处的导引方式为零提前角导引，即鱼雷的提前角为0，通常称该方法为追踪法或尾追法。

代入式（9）可得：

$ \frac{{\rm{d}} r}{{\rm{d}} t}=\frac{V_{T} {\rm{cos}} q_{t}-V_{V}}{-V_{T} {\rm{sin}} q_{t}} 。$

(10)

尾追法的弹道示意图如图5所示。不难发现，鱼雷始终指向目标航行。相比而言，纯追踪法对自导系统的参数要求比较少，仅需得出目标处于鱼雷纵轴4个方向的位置，即可控制鱼雷对准目标。因其实现简单，所以该方法最早被广泛应用于自导鱼雷。

2.2 固定提前角法

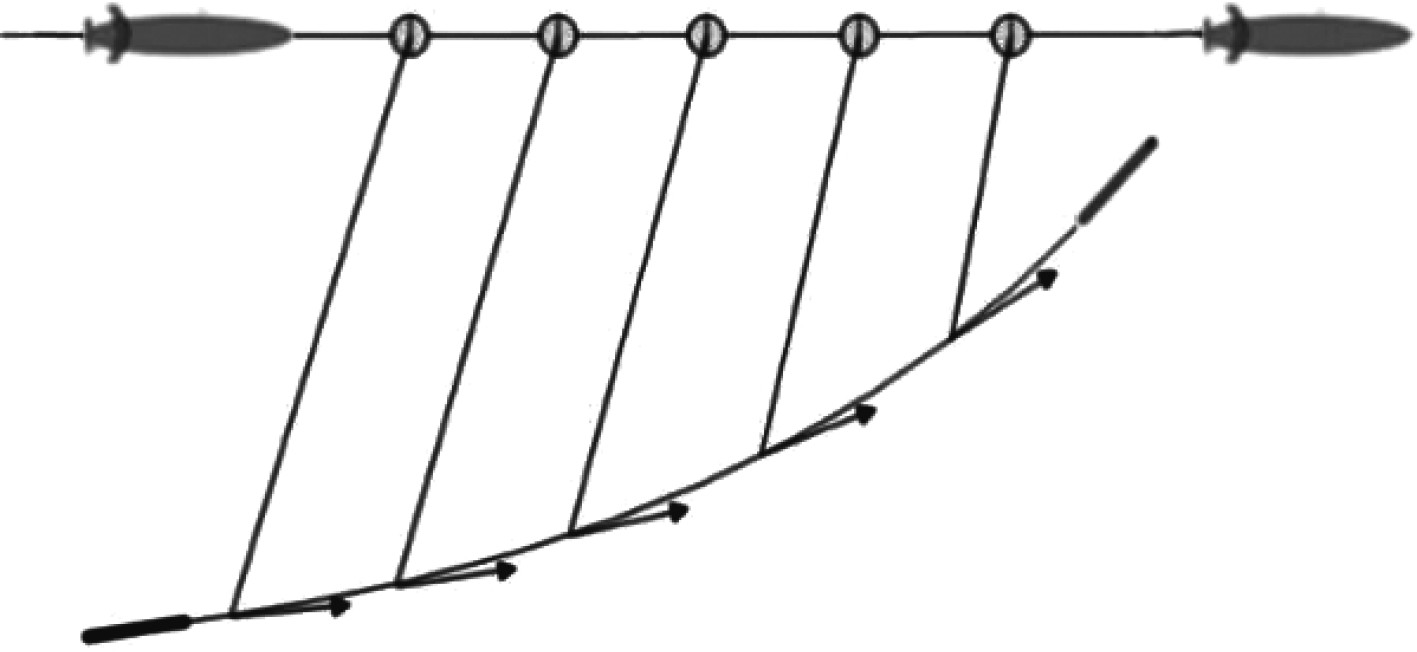
在导引过程时，使鱼雷运动方向与鱼雷目标视线保持一个固定角度的方法称为固定提前角法^[23-24]，如图6所示。

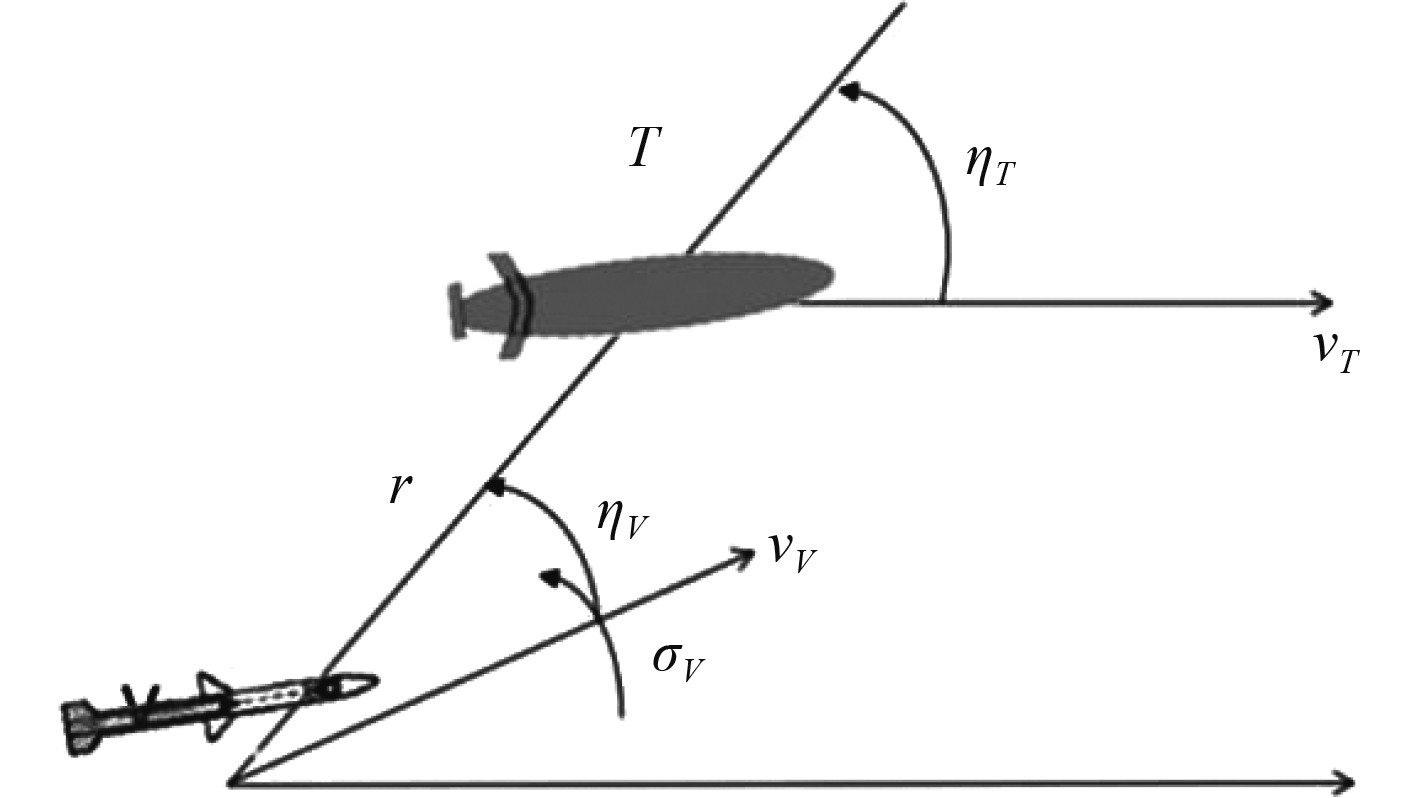
与尾追法相比，固定提前角法的优点是可通过选择合适的提前角使弹道平直，从而降低对鱼雷机动性的要求，同时也改变了尾追法只能命中目标尾部的局限性。固定提前角法的原理如图7所示。

此处，鱼雷的提前角为常数。代入式（9）可得：

$ \left\{\begin{split}&\dot r =V_T {\rm{cos}} \eta_T-V_V {\rm{cos}} \eta_v，\\ & r\dot q=V_V {\rm{sin}} \eta_V-V_T {\rm{sin}} \eta_T。\end{split} \right. $

(11)

2.3 平行接近法

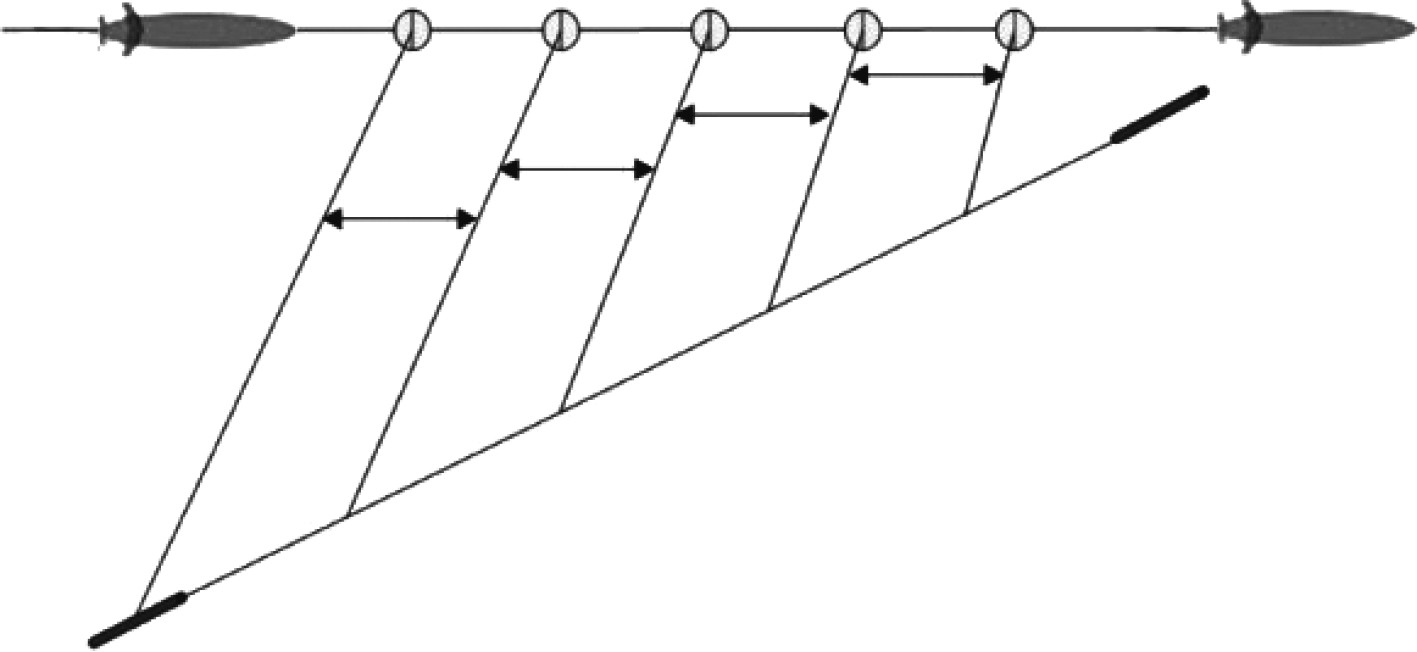
平行接近法^[23-24]是一种导引方法，通过维持鱼雷目标视线与初始鱼雷目标视线平行来进行。它在任何情况下（包括目标速度的大小和方向的变化）使视线保持平行于自身的移动。在平行接近法中，鱼雷中心与目标中心之间的连线始终保持平行运动，如图8所示。

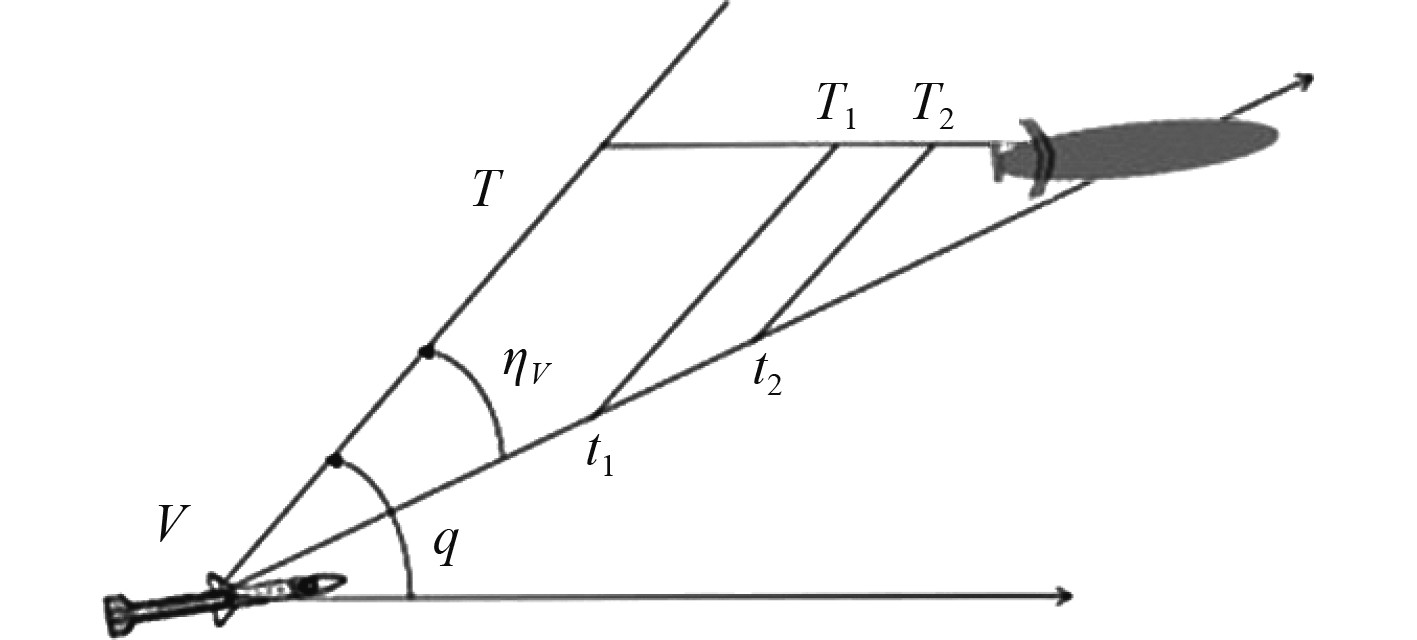
当鱼雷以及目标匀速运动时，则平行接近法的运动轨迹近似为直线^[25]，其原理图如图9所示。

导引过程相对运动方程为：

$ \left\{\begin{split}&\dot r =V_T {\rm{cos}} q_t-V_V {\rm{cos}} \eta_v，\\ &V_T {\rm{sin}} q_t=V_T {\rm{sin}} \eta _t。\end{split} \right. $

(12)

2.4 分析与比较

尾追法的优点在于制导系统简单，弹道简化。然而，其缺点在于不论从哪个方向发射，或是不同平台发射，鱼雷必须要绕到目标后面去命中，导致航程浪费且弹道弯曲程度较大，这样会导致鱼雷弹道完全性降低，法向过载较大。此外，尾追法的追踪速度有严格限制，在实际应用中较少。

固定提前角具有导引时间短的优点，与目标相遇时的舷向不与基线方向重合，从而增大了鱼雷击中目标时的破坏范围；缺点是随着鱼雷与目标的距离缩短，目标方位角的旋转速率增加。所以，当鱼雷离目标较远时，提前角调整应更为谨慎，避免过快的调整可能引起弹道的过度弯曲。

平行接近法优点是鱼雷机动性可小于目标的机动性，弹道曲率较小且速度可不受限制而实现全向攻击命中，过载不会很大；缺点是对制导系统要求很高，制导系统复杂。此外，当目标做圆周运动时，若目标与鱼雷距离较远，影响不大；但当鱼雷接近目标时，目标做圆周运动会导致舷角变化增大，相应法向载荷会增大，容易导致过载。

若目标做圆周运动时，选用固定提前角时，需选取合适的提前角。若提前角过大，可能会从目标运动前方穿过，增加鱼雷的脱靶概率；而过小可能会增加弹道距离，导致追击不到目标。当目标与鱼雷距离较远时，影响不大，但当鱼雷接近目标时会随着目标做圆周运动导致舷角变化过快，也容易导致过载。

若目标做圆周运动，当选用平行接近法时，需不断计算舷角，整个过程相对目标角度变化小。整个运动过程受目标运动较大，总结分析如表1所示。

3 基于LSTM的来袭鱼雷分类模型 3.1 LSTM网络结构介绍

循环神经网络(Recurrent Neural Network，RNN)通常被用来处理时间序列数据，因为该网络可根据先前时刻的输出以及当前时刻的输入，来决定当前时刻的输出，即RNN网络可将时间序列中不同时刻的数据关联起来。但当处理长时间序列数据时，RNN网络只能记忆距离较短的信息，这就会导致梯度消失与梯度爆炸问题。为解决这一问题，Hochreiter和Schmidhuber提出了长短期记忆网络(Long Short-Term Memory，LSTM)^[26]。

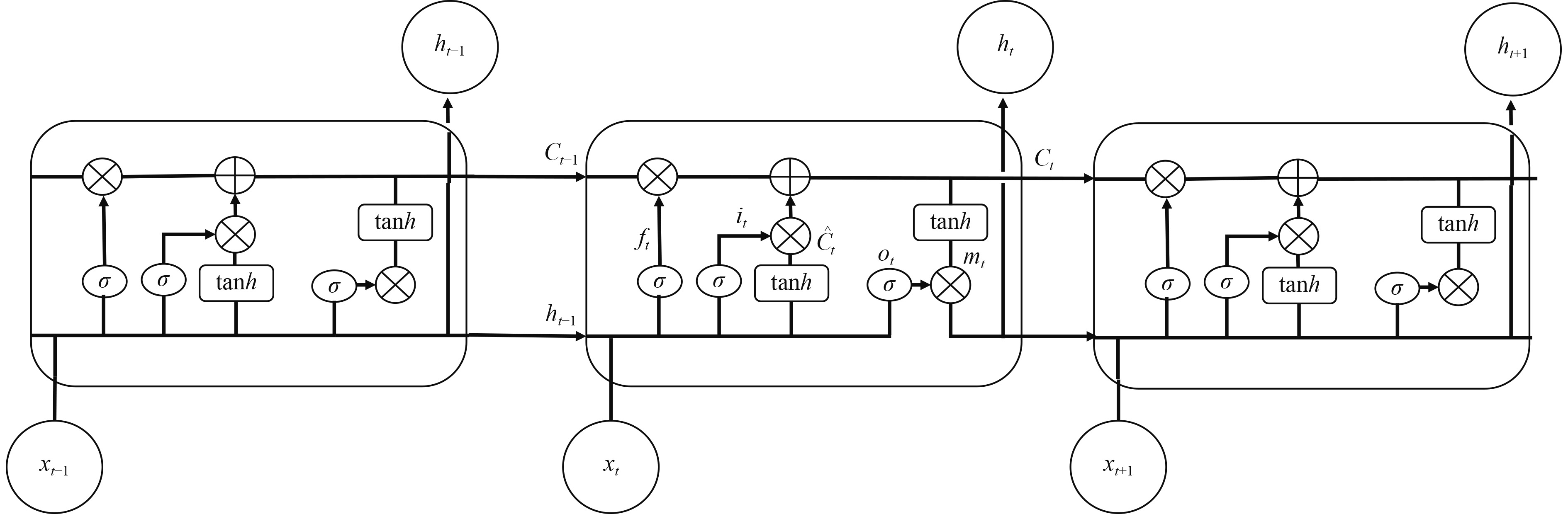
与标准的RNN网络相比，LSTM网络增加了一个记忆长时间信息的记忆单元块和3个门控单元：输入门、遗忘门和输出门，图10为LSTM网络的结构图。

图中x_t代表当前时刻的输入数据；c_t−1为上一时刻的单元状态；h_t−1为上一时刻的输出；c_t为当前记忆单元状态；h_t代表t时刻的输出值。输入门i_t决定了要传送给记忆单元的信息量，计算公式为：

$ i_{t}=\sigma\left(W_{i} \cdot\left[h_{t-1}, x_{t}\right]+b_{i}\right)。$

(13)

式中： $ \sigma$ 为Sigmoid函数，用于将i_t的值限制在0～1之间。当i_t为1时，表示当前时刻的输入全部传递给记忆单元；而i_t为0时，则完全舍弃。其中，W_i为输入门权重矩阵，b_i为输入门的偏置项。

遗忘门f_t可控制记忆单元的记忆和遗忘，决定上一时刻的记忆单元有多少数据将传递到当前时刻。具体而言，遗忘门的计算公式为：

$ f_{t}=\sigma\left({\boldsymbol{W}}_{f}\cdot \left[h_{t-1}, x_{t}\right]+b_{f}\right) 。$

(14)

式中：W_f表示遗忘门的权重矩阵；b_f为遗忘门的偏置项； $ \hat c_t$ 为备选更新当前状态的向量，其计算公式为：

$ \hat {{c}}_t={\rm{tan}}{\rm{h}}({\boldsymbol{W}}_c\cdot [h_{t-1},x_t]+b_c) 。$

(15)

式中：tanh为双曲正切激活函数；W_c，b_c为其权重矩阵和偏置项。当前时刻记忆单元状态c_t由上一时刻记忆单元的状态的和当前时刻的输入共同决定。计算表达式为：

$ c_t=f_t\cdot c_{t-1}+i_t\cdot \hat c_t ，$

(16)

输出门决定将记忆单元中的多少信息传送给当前的输出。计算公式为：

$ o_{t}=\sigma\left(W_{o} \cdot\left[h_{t-1}, x_{t}\right]+b_{o}\right)。$

(17)

式中：W_o，b_o为其权重矩阵和偏置项。

网络最终的输出由输出门和当前时刻记忆单元状态共同决定，当前时刻网络的输出为：

$ h_{t}=o_{t} \cdot {\rm{tan}} h \left(c_{t}\right)。$

(18)

3.2 来袭鱼雷态势判断网络模型的设计

根据以往经验，选用鱼雷的速度、目标速度、与目标距离、鱼雷与目标距离的变化量、鱼雷方位角和鱼雷方位角的变化量等6种特征序列数据作为分类网络的输入特征。模型的输出为已介绍的3种鱼雷类别。

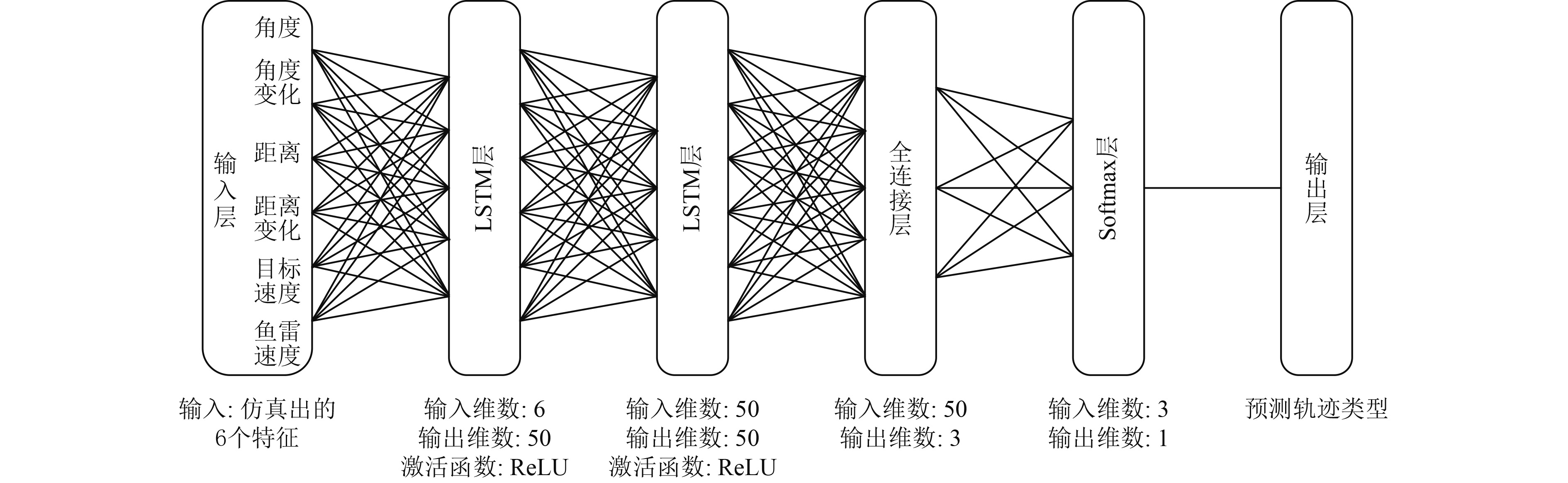
该模型的每个输入样本是一个50×6的矩阵，50代表50个时间步长，每个时间步长的间隔为20 ms，6代表输入的6维特征。将样本输入到LSTM模型中。如图11所示，模型包含1个输入层，2个LSTM层，1个全连接层，1个SoftMax层和1个输出层。第1个LSTM层有50个神经元，输出为50维；第2个LSTM层有50个神经元，输出为50维；全连接层含50个神经元，输出为3维。最后连接1个SoftMax层，输出各种鱼雷类别的概率，选取其中概率最大的类别作为模型的最终输出。

为提高网络对鱼雷分类问题的拟合能力，在每个隐藏层后添加了ReLU激活函数。该激活函数计算简单高效，具有稀疏性，可有效缓解梯度消失、梯度爆炸以及过拟合问题。

3.3 仿真实验验证 3.3.1 数据集建立

使用Matlab建立3种来袭鱼雷攻击舰艇的运动模型，对6种特征进行采样，并通过设置不同的鱼雷参数进行多次仿真实验，得到8万个样本数据。

为确保所有类别在模型训练期间平等参与，随机对数据集进行比例划分。其中60%的数据集用于训练模型；20%的数据集用于模型验证，并进行调参验证；剩下20%的数据作为测试集进行模型的测试。

数据的归一化处理，采用最小-最大值归一化方法，将数值规范到 (0,1) 区间范围内，以消除量纲。综合使用各特征数据进行训练，有助于加快模型收敛速度，提高精度，防止梯度爆炸。

最小-最大值归一化处理的数学描述如下：

$ y=\frac{x-\min (x)}{\max (x)-\min (x)}。$

(19)

式中：x为样本值；min(x) 和max(x) 分别为数据中的最小值和最大值。

3.3.2 模型训练

将进行归一化处理的数据集放入LSTM网络模型中进行训练，并采用Adam优化器加速神经网络的训练。设置训练轮数为200，初始学习率设置为0.001，并根据训练的轮数动态调整学习率，每50轮将其衰减为之前的一半。选用批次大小为256，在GPU上进行训练。在训练过程中，保存了在验证集上测试准确率最高的模型。

在训练过程中，选用交叉熵函数为损失函数。交叉熵函数刻画了2个概率分布之间的距离，在分类问题上表现优秀。该函数的标准形式如下：

$ C=-\frac{1}{n} \sum_{x}[y \ln a+(1-y) \ln (1-a)]。$

(20)

式中：x为样本；y为实际标签；a为预测输出；n为样本总数。

为了防止模型过拟合，在模型的LSTM层中加入Dropout。Dropout可在模型的训练过程中以一定概率丢弃神经元，因此在每次迭代中训练的是不同网络。在训练过程中设置Dropout = 0.5。

为了增强模型的泛化能力，在损失函数中引入L₂正则化项，对大数值的权重向量进行惩罚，防止模型的过拟合。在训练过程中设置正则化系数为 $ 1 \times 10 ^{-4}$ 。其计算公式如下：

$ {L}={L}_{0}+\frac{\lambda}{2 {n}} \sum_{i=1}^{n} \omega_{i}^{2}。$

(21)

其中：L₀为原始损失函数； $ \lambda $ 为正则化系数；n为训练集样本总数； $ \omega$ 为权重。

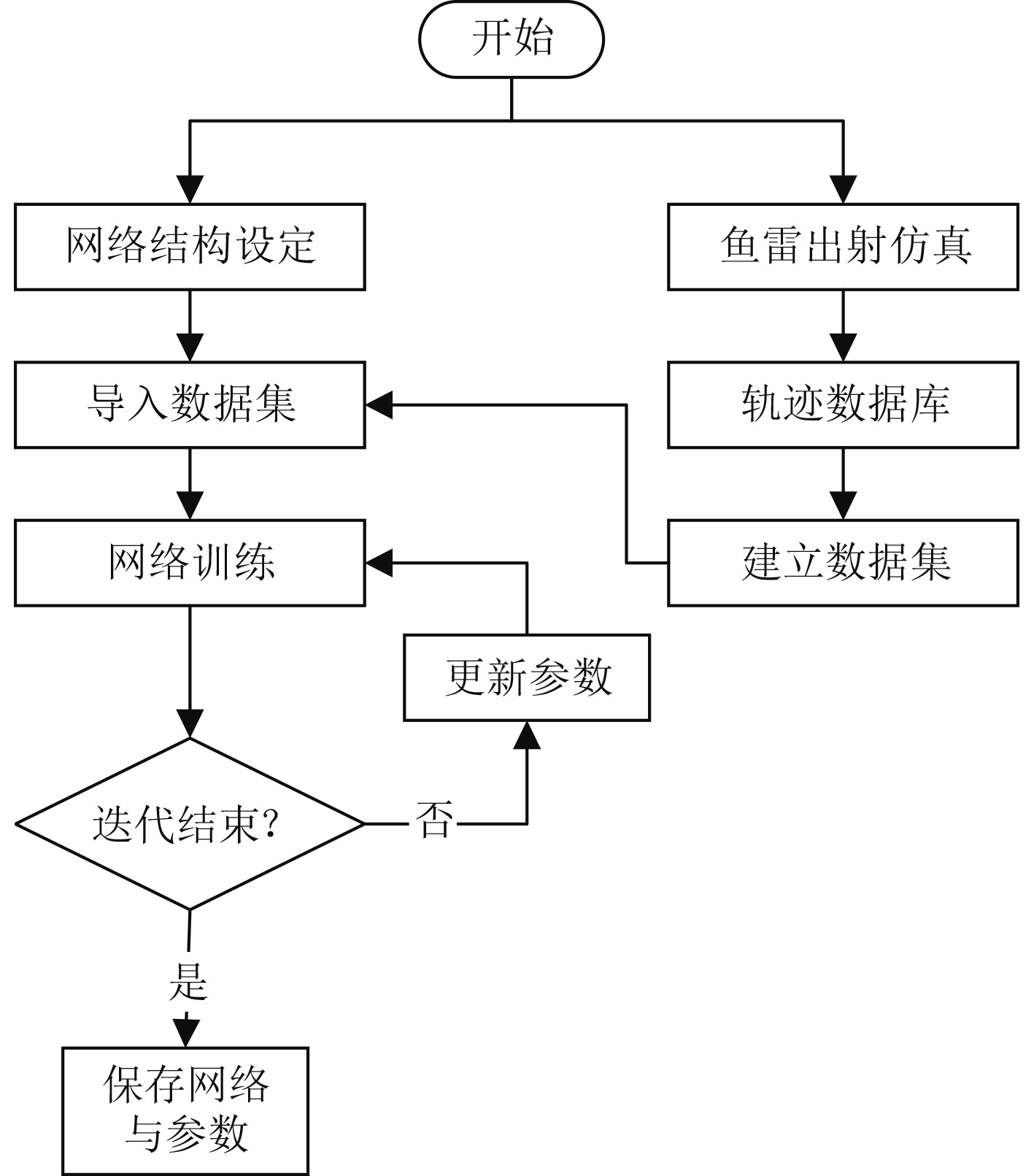
LSTM网络模型训练过程如图12所示。

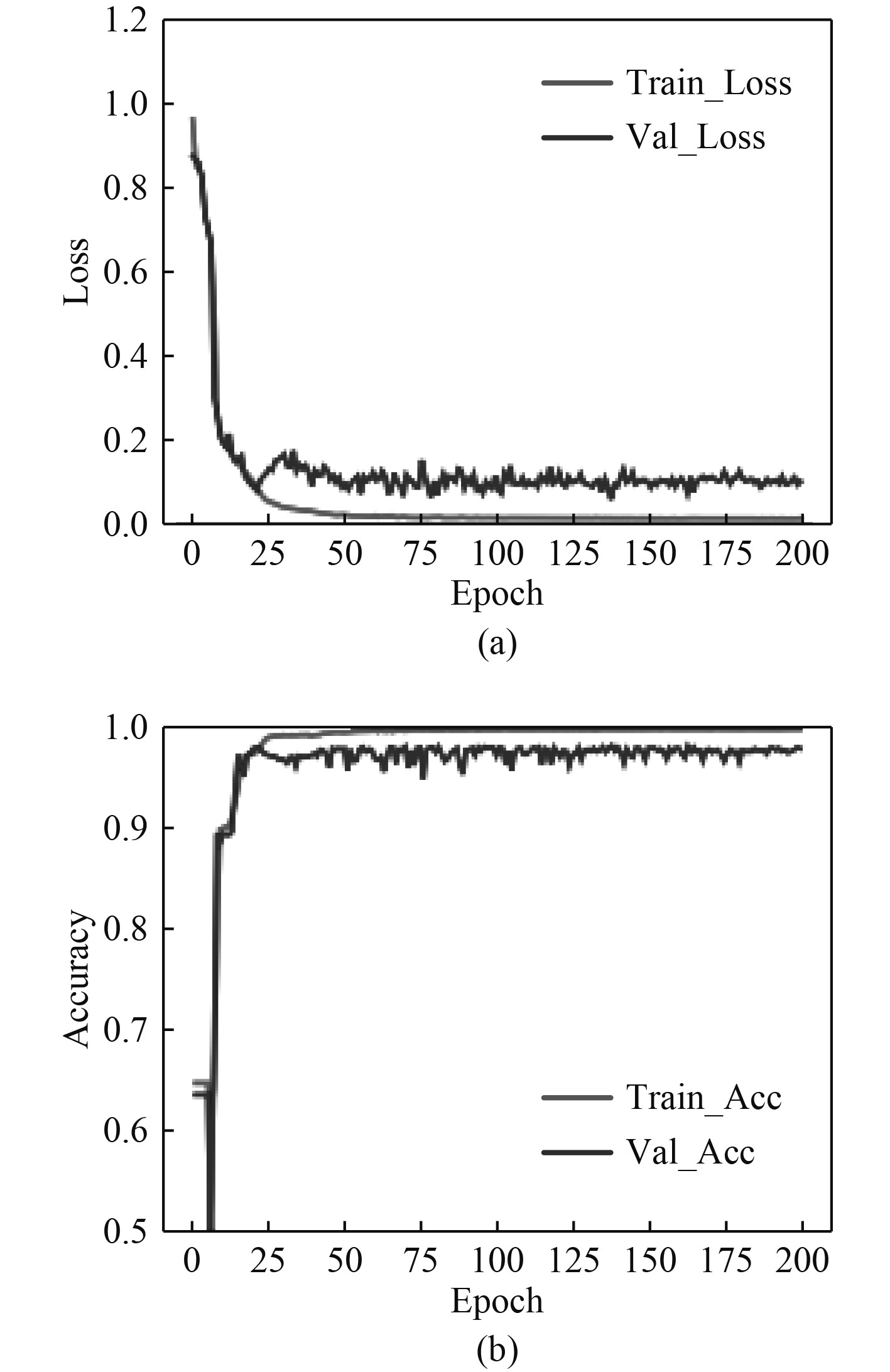
LSTM网络训练过程中训练集与验证集的损失函数值如图13(a)所示；图13(b)为训练集与验证集的正确率曲线图。在175轮后，训练集和验证集的损失函数值趋于稳定。

3.3.3 模型测试

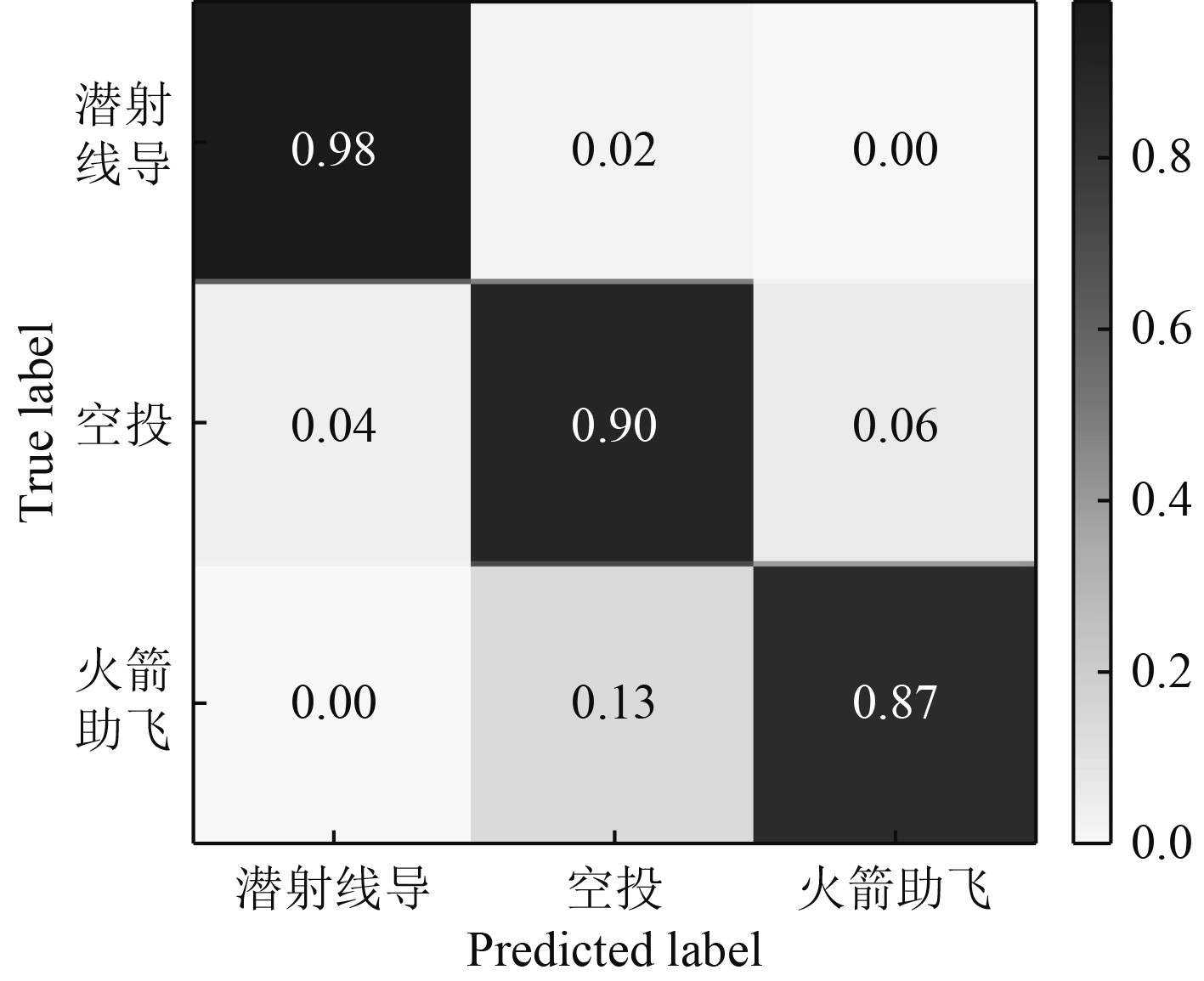
在模型训练完成后，对训练好的模型在测试集上进行测试。图14所示为LSTM模型测试所得的混淆矩阵。图中横坐标表示模型预测的类别，纵坐标表示数据集真实的类别。对角线上的值为得到正确分类的鱼雷类别，而未在对角线上的则表示错误分类的类别。经过测试，该模型最终的准确率达到了91.73%。

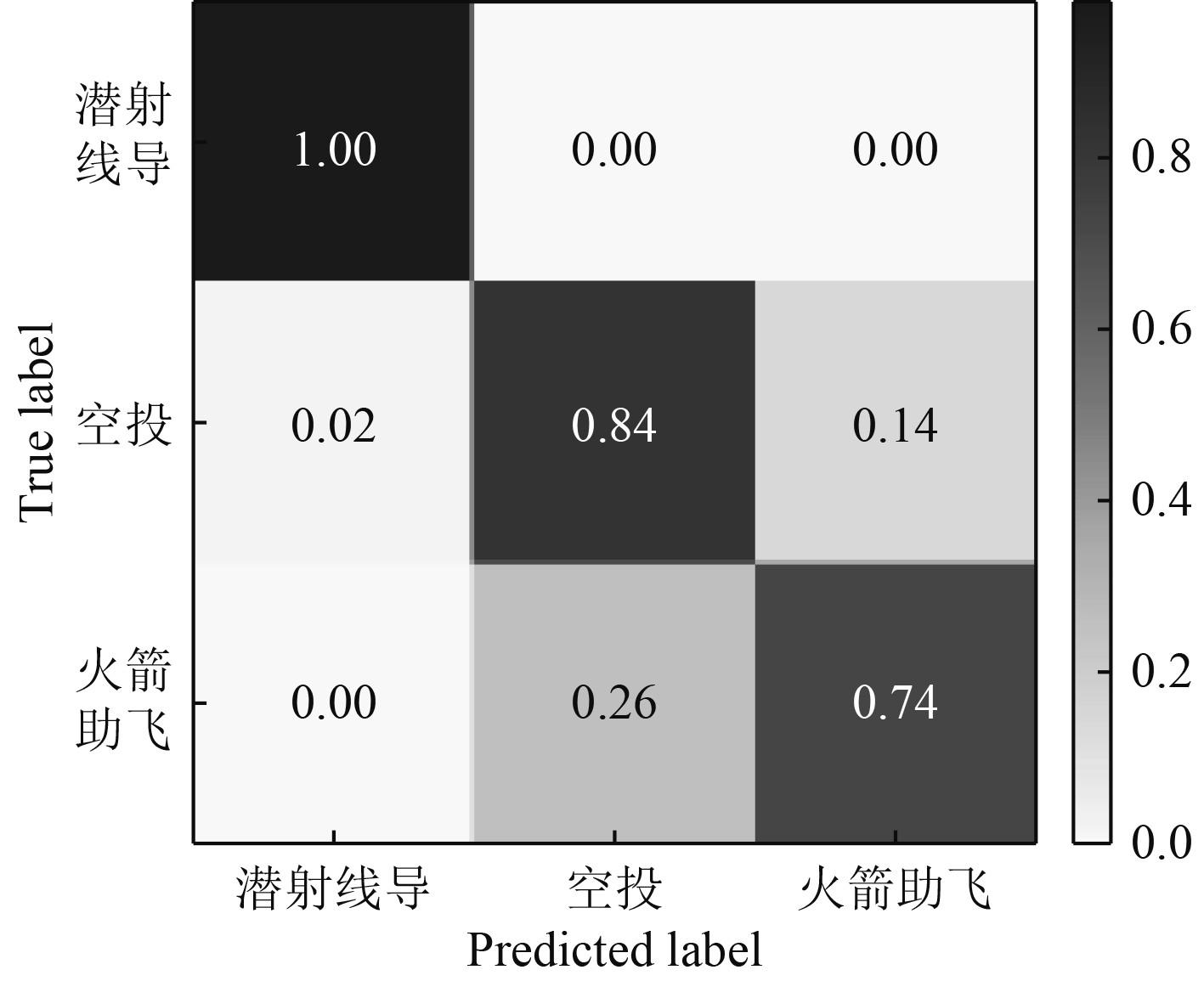
除了LSTM网络模型以外，本文也采用了1D-CNN网络对同一数据集进行学习和训练，其测试结果如图15所示，模型的准确率为86.55%。然而，与LSTM模型相比，该模型在各个类别的识别准确率上表现并不理想，尤其是火箭助飞来袭鱼雷容易与空投来袭鱼雷混淆。因此，LSTM网络的分类模型相较1D-CNN网络模型性能方面更加出色。

为了更全面评估2个网络的性能，引入召回率（Recall）、精确率（Precision）和F1-Score分析这2个模型。其计算过程如下：

$ \left\{\begin{split}&Precision=\frac{TP}{TP+FP}，\\ &Recall= \dfrac{TP}{TP+FN}，\\ &F1-Score= \dfrac{2\times Precision \times Recall}{Precision+Recall}。\end{split} \right. $

(22)

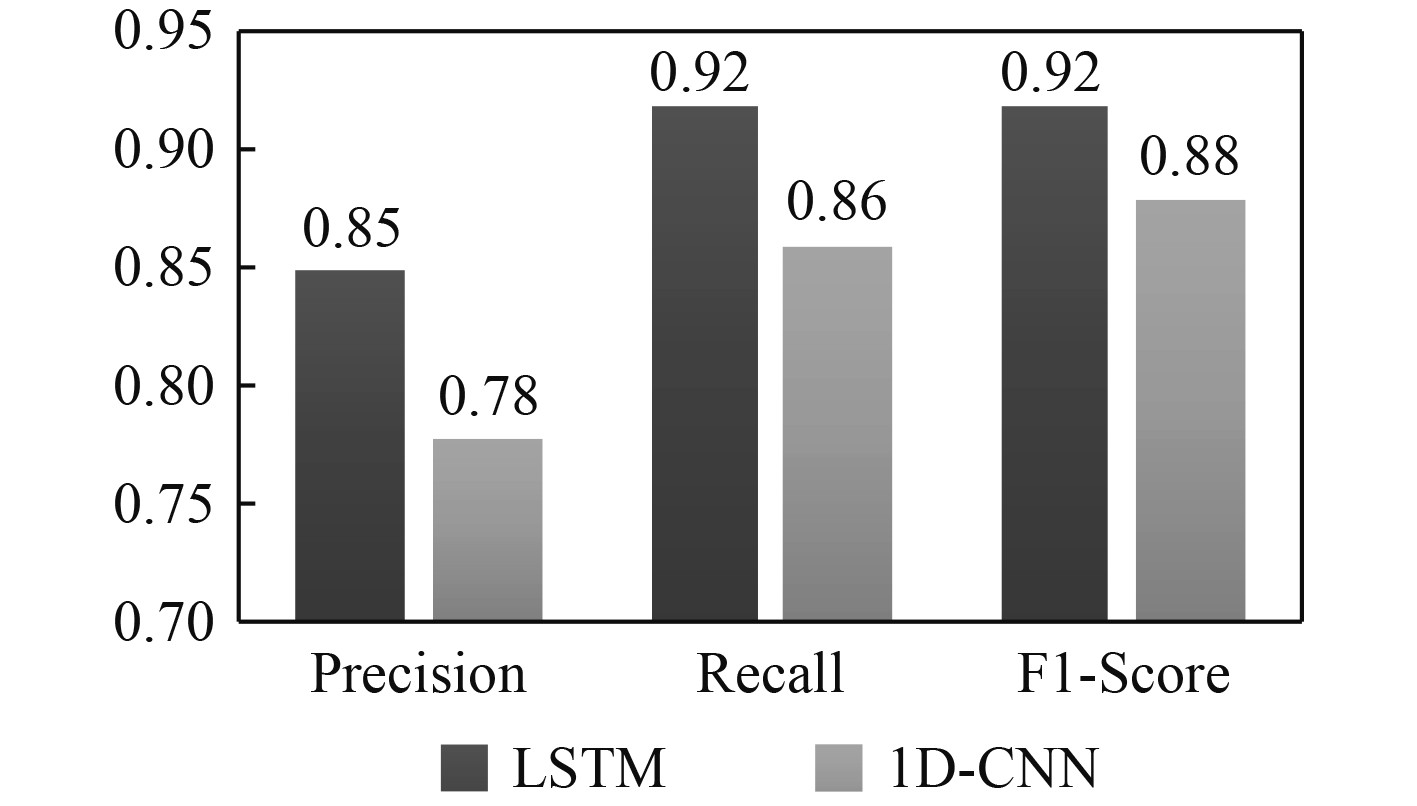
其中：TP为将正类正确判定为正类；FP为将负类错误判定为正类；FN为将正类错误判定为负类；TN为将负类正确判定为负类。图16为2种模型的指标对比。

从结果来看，相较于1D-CNN模型，LSTM模型的漏报现象和误报现象更少，性能更加优越。

4 结　语

针对3种鱼雷的弹道分类问题，本文提出一种基于LSTM网络的分类方法。得益于其强大的非线性拟合能力和对时间序列的记忆功能，该方法可在较少迭代轮数下得到相对较高的判断准确度。

结果表明，本文所提出的来袭鱼雷分类模型，分类准确度和适用性都能够很好地实现对鱼雷类型的识别，为后续舰艇提出反制手段打下技术基础。下一步工作的重点是，在不损失准确度的情况下，减少运动要素的获取，降低对信息的依赖度。