鱼雷是一种涉及机械、电子、力学、动力、控制、水声、爆炸等多学科的高技术水下精确制导武器[1]。由于使用平台多样,在其全寿命周期内要经历运输、装载、贮存、空中飞行、入水、水下航行等多个环节,所经历的振动环境十分复杂,会经受各种随机激励。如发动机振动引起的激励,水下航行时湍流噪声引起的激励,螺旋桨运转产生的随机激励等。这些激励通过雷体传递到自导系统各组件上面,引起组件的振动。这些振动噪声是鱼雷实现目标探测与识别的主要干扰背景,降低振动噪声干扰,可以有效提升鱼雷目标探测距离、识别正确率、精确打击效果等重要作战性能。
基阵支撑结构位于鱼雷自导头段内部,起到连接声学基阵和头段壳体的作用。在鱼雷航行过程中,来自后部动力舱段的振动噪声通过鱼雷壳体及内部组件传递到基阵支撑结构处,进而传递到声学基阵内,因此对基阵支撑结构进行有效的减振设计十分必要。目前在基阵支撑结构设计过程中主要通过吸声、隔振材料等,降低传递过来的振动能量。但是,由于吸声、隔阵材料的性能随频率的降低而变差,对中、高频段噪声较为有效,对低频噪声效果不大,迫切需要应用新的宽带减振技术。
声学黑洞(Acoustic Black Hole,ABH)由于其具有高效、轻质、宽频等特性,受到众多工程技术人员关注。其基本原理是通过结构阻抗变化,使结构中传播的波相速度和群速度相应改变,能量在局部黑洞区域实现聚集。国内外有关ABH的研究主要聚焦在ABH的减振机理及提高声学黑洞效应等方面,如Krylov等[2-4]通过实验方法测试了阻尼材料对非完美声学黑洞效应的补偿效果;Conlon和Cheng等[5-6]探究了自由场中ABH结构波数演变与辐射机制;O’Boy等[7-8]研究了平台长度对声学黑洞效应的影响;Ding和Zheng等[9-10]建立了声学黑洞动力学模型,分析了声学黑洞的能量聚集特性。Tang等[11]提出2种“双叶型”声学黑洞梁结构,通过周期排布3个原胞结构形成梁,通过试验测试了梁的减振带隙,结果表明。这种结构可有效拓宽减振频带,极大提高了减振性能。但这些研究对象均为板、梁等简单结构,缺乏工程应用案例。针对鱼雷基阵支撑结构这种复杂结构的减振设计问题尚无相关研究,本文借鉴“双叶型”声学黑洞梁结构,结合鱼雷自导结构特点及安装方式,提出一种多边形减振环结构,通过试验测试分析了该结构的减振效果,为鱼雷自导基阵支撑结构的减振设计提供参考。
1 声学黑洞基本原理在薄板楔形结构中,如果结构的厚度以幂函数
弯曲波在二维声学黑洞结构中传播的控制方程为[12]:
| $ \begin{split} \frac{{{\partial ^2}}}{{\partial {x^2}}}&\left[ {D(x,y)\left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \mu \frac{{{\partial ^2}w}}{{\partial {y^2}}}} \right)} \right] +\\ &2(1 - \mu )\frac{{{\partial ^2}}}{{\partial x\partial y}}\left[ {D(x,y)\frac{{{\partial ^2}w}}{{\partial x\partial y}}} \right] + \frac{{{\partial ^2}}}{{\partial {y^2}}}\left[ D(x,y)\left( \frac{{{\partial ^2}w}}{{\partial {y^2}}} +\right.\right. \\ & \left.\left.\mu \frac{{{\partial ^2}w}}{{\partial {x^2}}} \right) \right] - {\omega ^2}\rho h(x,y)w = 0 。\\[-15pt] \end{split} $ | (1) |
式中:
| $ w(x,y) = A(x,y){e^{i{k_p}\varphi (x,y)}}。$ | (2) |
式中:
| $k(x,y) = {12^{1/4}}{k_p}^{1/2}{\left[ {h(x,y)} \right]^{ - 1/2}},$ | (3) |
式中,
| $ \varPhi = \int_0^x {k(x){\rm{d}}x}。$ | (4) |
由式(3)和式(4)可看到,当
鱼雷自导基阵支撑结构是鱼雷发动机机械振动传递到换能器接收端的重要途径之一。本文以某型号鱼雷自导结构为基础,利用声学黑洞原理对基阵支撑结构进行减振设计,提出一种多边形环减振结构。结构由10根减振梁首尾相连形成正10边形,如图1所示。多边形的每条边均为相同的减振梁结构,共分为2种结构形式:一种为“双叶型”声学黑洞结构,减振梁I(见图2);另一种在“双叶型”结构中间添加方形块减振梁II(见图3)。多边形减振环采用不锈钢一体加工而成,整个结构外轮廓不超过直径φ377 mm的圆。2种减振梁的尺寸图如图4和图5所示。结构控制参数经过多轮优化,同时考虑到结构5~10 kHz频带减振问题,最终定义声学黑洞幂率曲线参数为

|
图 1 多边形减振环 Fig. 1 Polygon damping ring |

|
图 2 减振梁I Fig. 2 Vibration reduction beam I |

|
图 3 减振梁II Fig. 3 Vibration reduction beam II |

|
图 4 减振梁I尺寸图 Fig. 4 Dimension drawing of vibration reduction beam I |
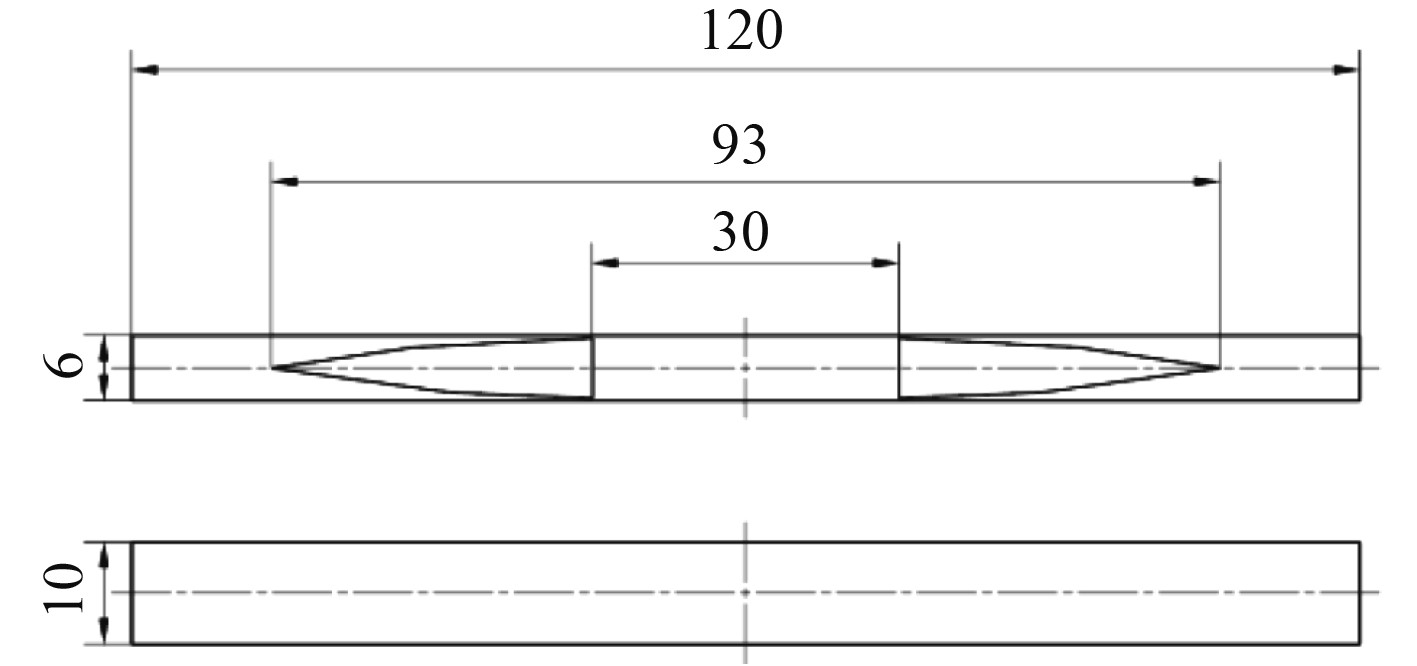
|
图 5 减振梁II尺寸图 Fig. 5 Dimension drawing of vibration reduction beam II |
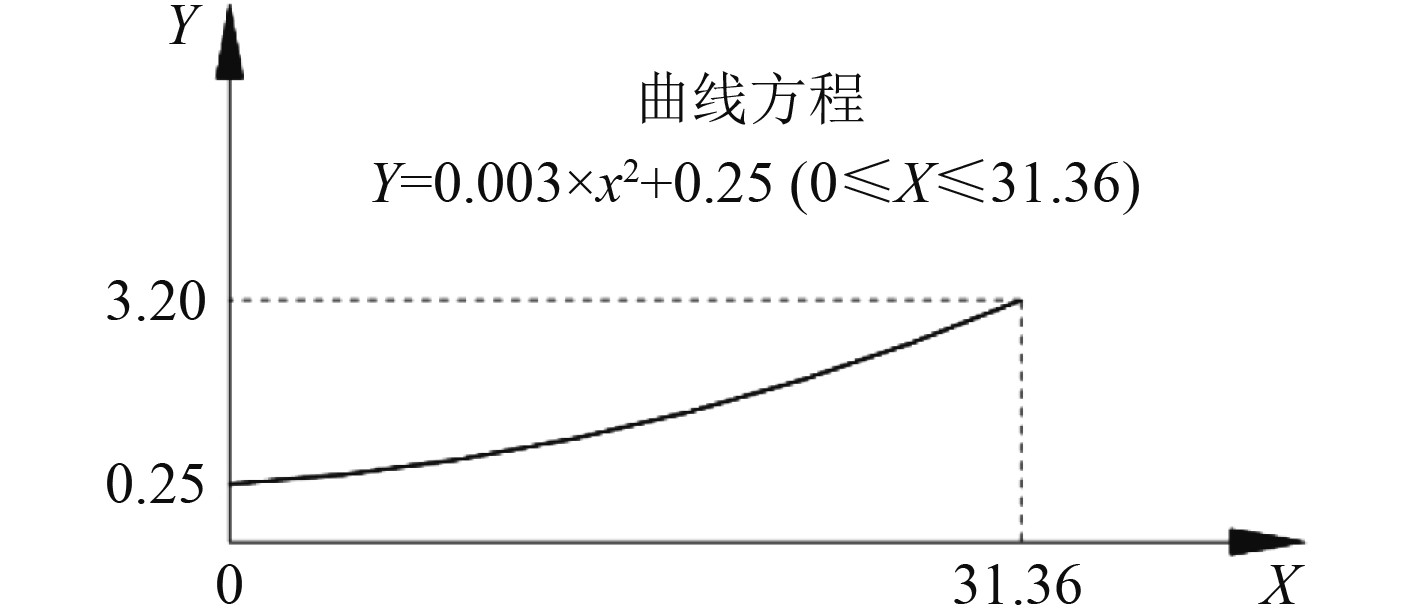
|
图 6 曲线方程 Fig. 6 Curve equation |

|
图 7 减振梁样机 Fig. 7 The prototype of vibration reduction beam |

|
图 8 多边形减振环样机 Fig. 8 The prototype of polygon damping ring |
采用悬吊装置对样机进行固定安装,悬吊装置由固定支架和弹性绳组成,其中固定支架具有足够的刚度,能够确保被测样件的安全;弹性绳具有合理的刚度,满足试验测试的要求,减少对被测样机的影响。试验采用激振器激励,激励方向分为轴向(多边形减振环轴心方向),在激励点附近和远离激励点位置布置加速度传感器用于采集数据。试验原理示意图如图9所示,测点布置如图10所示。

|
图 9 试验原理图 Fig. 9 Schematic diagram of test |
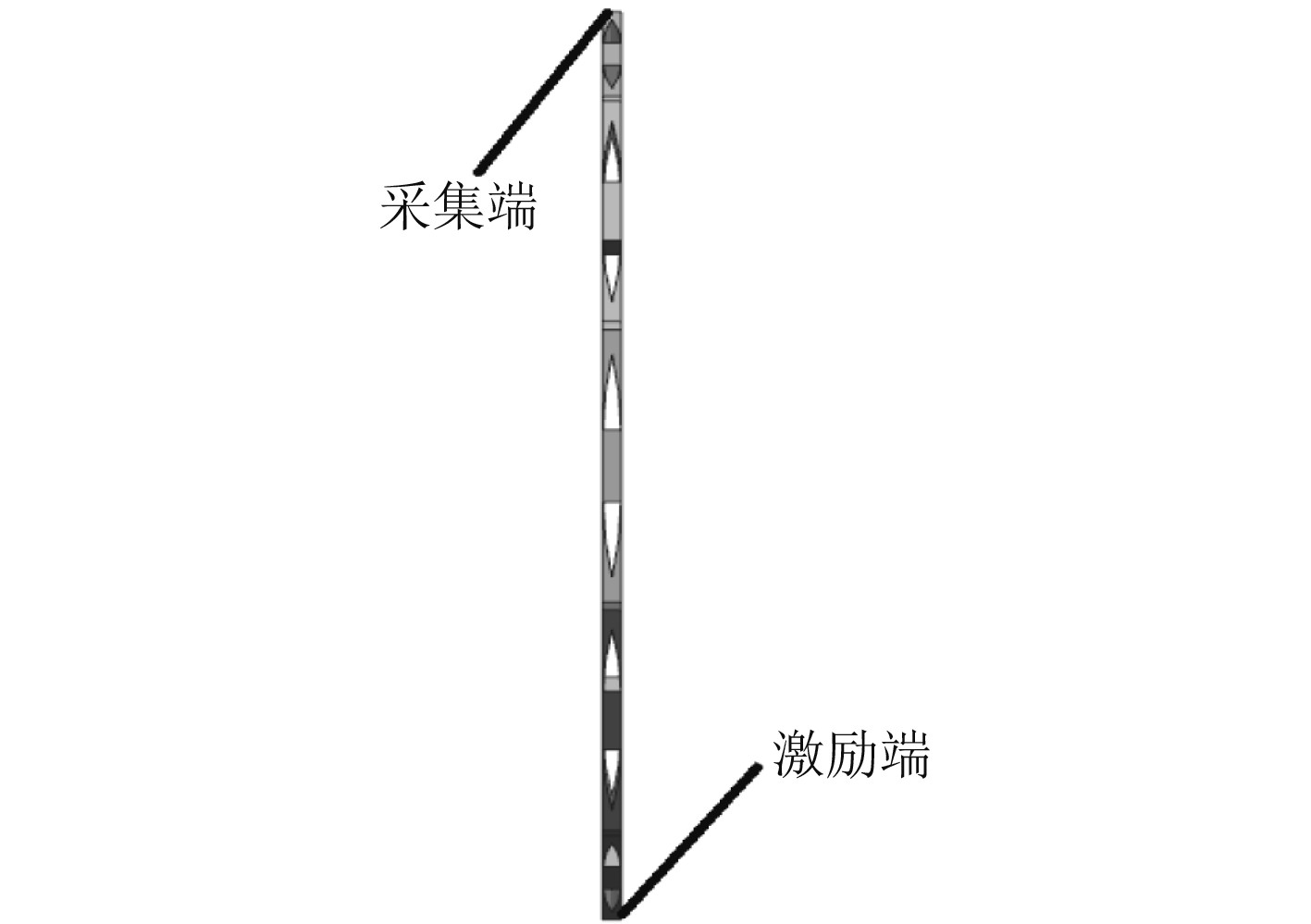
|
图 10 测点布置 Fig. 10 Arrangement of measuring points |
测试时,在测试设备许用量程范围内尽可能拓宽测试频带,同时考虑工程实际,将测试频带分为9个范围。首先划分3个频带最宽的频段,分别为50~1 000 Hz、50~2 000 Hz和50~10 000 Hz,其次针对50~2 000 Hz低频段又细分为50~500 Hz、500~1 000 Hz、1000~1 500 Hz和1500~2 000 Hz 4个频段,最后针对鱼雷发动机工作轴频又划分了100~200 Hz和200~300 Hz 2个频段。频段划分情况如图11及表1所示。
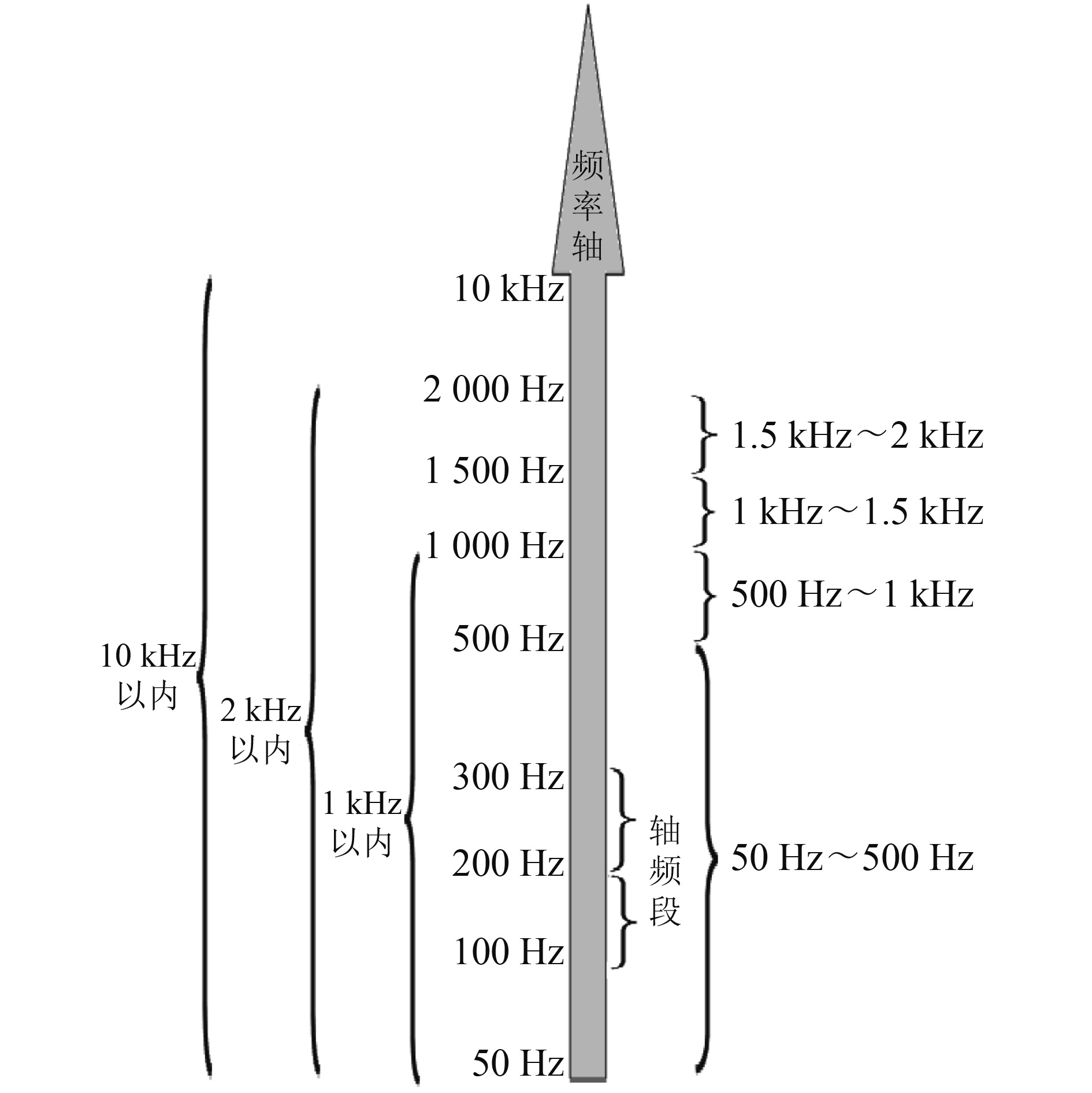
|
图 11 测试频带划分 Fig. 11 Test band division |
|
|
表 1 测试频带划分情况 Tab.1 Test band division |
采集到的测试数据通过加速度振级算法得到激励端和采集端的加速度振级,二者求差得到振级落差数据,试验结果以此来评估减振措施的减振效果,加速度振级计算公式为:
| $ {L_a} = 20\log \Bigg(\frac{{{A_e}}}{{{A_0}}}\Bigg) 。$ | (5) |
其中:
振级落差计算公式为:
| $ TL={L}_{激励端}-{\text{L}}_{采集端}。$ | (6) |
其中:
对样机进行测试时,设置5种状态做对比,分别是1个圆环(减振梁I结构形式),记为状态1;1个圆环(减振梁II结构形式),记为状态2;2个圆环(均为减振梁I结构形式),记为状态3;2个圆环(均为减振梁II结构形式),记为状态4;2个圆环(1个为减振梁I结构形式,另1个为减振梁II结构形式),记为状态5。2个多边形减振环通过螺钉和垫柱连接在一起,如图12所示。

|
图 12 连接方式 Fig. 12 The connection method |
试验测试数据如表2所示,对几种状态中振级落差数值高的一方字体变粗,以便于对比减振效果。
|
|
表 2 振级落差测试结果(dB) Tab.2 Test results |
通过表2中数据可以看出:单层多边形环(中间空心)减振性能总体上优于单层多边形环(中间有块);双层多边形环(中间空心)减振性能总体上优于单层多边形环(中间空心);双层多边形环(中间有块)减振性能总体上优于单层多边形环(中间有块);总体上看,在双层多边形环中,减振性能从弱到强顺序为双层多边形环(中间有块)<双层多边形环(一样一个)<双层多边形环(中间空心)。特别的,双层多边形环(中间空心)结构的减振性能远高于其他结构,减振效果十分明显。
综合来看,所设计的基于声学黑洞原理的多边形减振环不仅在低频段有良好的减振效果,在高频段同样有良好的减振效果。在鱼雷自导基阵支撑结构减振设计时,采用若干个多边形减振环结构串联在一起使用,将会取得优异的减振效果。
4 结 语本文针对鱼雷自导基阵支撑结构设计一种基于声学黑洞原理的多边形减振环,并测试其减振性能,详细说明了测试方法、激励频段设置、数据采集及处理方法,并对试验结果进行了分析。结果表明,所设计的多边形减振圆环在低频段和高频段均具有良好的减振效果。研究成果对鱼雷自导基阵支撑结构减振设计具有一定参考价值。
| [1] |
尹韶平, 刘瑞生. 鱼雷总体技术[M]. 北京: 国防工业出版社, 2011
|
| [2] |
BOWYER E P, KRYLOV V V. Damping of flexural vibrations in turbofan blades using the acoustic black hole effect[J]. Applied Acoustics, 2014, 76: 359-365. DOI:10.1016/j.apacoust.2013.09.009 |
| [3] |
BOWYER E P, O’BOY D J, KRYLOV V V, et al. Ex- perimental investigation of damping flexural vibrations in plates containing tapered indentations of power-law profile[J]. Applied Acoustics, 2013, 74(4): 553-560. DOI:10.1016/j.apacoust.2012.10.004 |
| [4] |
KRYLOV V. Acoustic black holes: recent develop- ments in the theory and applications[J]. IEEE Trans Ul- trason Ferroelectr Freq Control, 2014, 61(8): 1296-1306. DOI:10.1109/TUFFC.2014.3036 |
| [5] |
FEURTADO P A, CONLON, S C. Wavenumber trans- form analysis for acoustic black hole design[J]. The Journal of the Acoustical Society of America, 2016, 140(1): 718-727. DOI:10.1121/1.4959023 |
| [6] |
MA L, CHENG L. Sound radiation and transonic boundaries of a plate with an acoustic black hole[J]. The Journal of the Acoustical Society of America, 2019, 145(1): 164-172. DOI:10.1121/1.5081680 |
| [7] |
O’BOY D J, KRYLOV V V, KRALOVIC V. Damping of flexural vibrations in rectangular plates using the acoustic black hole effect[J]. Journal of Sound and Vi- bration, 2010, 329(2010): 4672-4688. |
| [8] |
BOWYER E P, NASH P, KRYLOV V V. Damping of flexural vibrations in glass fiber composite plates and honeycomb sandwich panels containing indentations of power-law profile[J]. Journal of the Acoustical Society of America, 2013, 132(3): 2041. |
| [9] |
LI X, DING Q. Analysis on vibration energy concentra- tion of the one-dimensional wedge-shaped acoustic black hole structure[J]. Journal of Intelligent Material Systems and Structures, 2018, 29(10): 2137-2148. DOI:10.1177/1045389X18758184 |
| [10] |
曾鹏云, 郑玲, 左益芳, 等. 基于半解析法的一维圆锥形声学黑洞梁能量聚集效应研究[J]. 噪声与振动控制, 2018, 38(S1): 210-214. ZENG P Y, ZHENG L, ZUO Y F, et al. Analysis of theenergy concentration effect of flexural vibrations in ta-pered rods with power-law profile based on semi-analytical method[J]. Noise And Vibration Control, 2018, 38(S1): 210-214. DOI:10.3969/j.issn.1006-1355.2018.Z1.044 |
| [11] |
L. Tang and L. Cheng, Ultrawide band gaps in beams with double-leaf acoustic black hole indentations [J]. The Journal of the Acoustical Society of America, 2017. 142: 2802.
|
| [12] |
季宏丽, 黄薇, 裘进浩, 等. 声学黑洞结构应用中的力学问题. 力学进展, 2017, 47: 201710. JI H L, HUANG W, QIU J H, et al. Mechanics problems in application of acoustic black hole structure. Advances in Mechanics, 2017, 47: 201710. |
 2023, Vol. 45
2023, Vol. 45
