0 引　言

船舶型线优化设计是指通过对船舶的外形和型线进行优化，以提高船舶的性能和效率。船舶型线优化设计的目标是减小船舶的阻力，提高航行速度、节省燃油消耗和减少排放，同时保持船舶的稳定性和安全性。通常船舶阻力主要包括摩擦阻力、波浪阻力和空气阻力等，在船舶型线优化时，可以通过调整船舶的船首形状、船尾形状和船体的横截面形状等来优化船舶的船型，减小波浪阻力和空气阻力。通过调整船舶的长宽比、船舶的吃水深度和船舶的排水量等来优化船舶的船体尺寸，提高航行速度和节省船舶的燃油消耗。

船舶型线优化设计是一个多目标寻优问题，本文以非均匀有理B样条(NURBS样条)为优化的基础，使用计算机辅助软件进行船舶的流体动力学特性分析，对船舶型线优化的阻力特性进行了有限元仿真。

1 NURBS样条曲线的基本研究

NURBS样条是由一系列控制点、权重和节点向量定义的，其中，控制点确定了曲线或曲面的形状，权重用于调整控制点对曲线或曲面的影响程度，节点向量决定了曲线或曲面的参数化方式。与其他样条方法相比，NURBS样条具有以下特点：

1）非均匀性。节点向量可以非均匀地分布，使得曲线或曲面在不同区域具有不同的密度，从而更好地适应复杂形状。

2）有理性。NURBS样条允许控制点具有不同的权重，通过调整权重可以改变曲线或曲面的形状，使得NURBS样条能够表示更广泛的曲线和曲面。

3）局部控制性。修改一个控制点只会影响曲线或曲面的局部区域，不会对整个曲线或曲面产生影响，这使得NURBS样条更易于编辑和调整^[1]。

NURBS样条的定义如下：

定义控制点矢量 $T\left( {{t_0},{t_1},...,{t_n}} \right)$ ，且 ${t_i} < {t_{i + 1}}$ ，则得到第i个p次B样条基函数定义如下：

$\left\{ {\begin{array}{*{20}{l}} {{{{N}}_{i,0}}({{t}}) = \left\{ {\begin{array}{*{20}{l}} 1,& {{{t}}_i} \leqslant {{t}} < {{{t}}_{i + 1}}，\\ 0,& {\rm{else}} ，\end{array}} \right.} \\ {{{{N}}_{i,p}}({{t}}) = \dfrac{{{{t}} - {{{t}}_i}}}{{{{{t}}_{i + p}} - {{{t}}_i}}}{{{N}}_{i,p - 1}}({{t}}) + \dfrac{{{{{t}}_{i + p + 1}}}}{{{{{t}}_{{{i}} + 1}}}}{{{N}}_{i + 1,p - 1}}(t)} ，{{\rm{else}}} 。\end{array}} \right.$

式中： ${{{N}}_{i,p}}({{t}})$ 为区间 $\left[ {{{{t}}_{{i}}},{{{t}}_{{{i}} + {{p}} + 1}}} \right]$ 上的分段函数，节点个数为P个。

NURBS样条的曲线方程可改写为：

$\begin{gathered} p(u) = \sum\limits_{i = 0}^n {{d_i}} {R_{i,p}}(u) \text{，} \\ {R_{i,p}}(u) = \frac{{{\omega _i}{N_{i,p}}(u)}}{{\displaystyle\sum\limits_{j = 0}^n {{\omega _i}} {N_{i,p}}(u)}}\text{。} \\ \end{gathered}$

式中：p为NURBS样条的幂次； ${R_{i,p}}(u)$ 为基函数。

NURBS样条的特性函数表达式如下：

1）递推特性

${{\text{N}}_{i,p}}({\text{t}}) = F\left( {{{\text{N}}_{{\text{i}},p - 1}}({\text{t}})} \right) \text{，}$

2）归一性

$\sum\limits_{i = 0}^n {{N_{i,p}}} (t) = 1 。$

3）局部区间支撑性^[2]

${N_{t,p}}(t)\left\{ {\begin{array}{*{20}{l}} { \geqslant 0}，&{t \in \left[ {{t_i},{t_{i + p + 1}}} \right]}，\\ { = 0}，&{{\text{else}}} 。\end{array}} \right.$

4）非负性

${N_{t,p}}(t) \geqslant 0 。$

基于NURBS样条的曲线构造过程如下：

1）分别构造曲线 ${C_i}\left( {i = 1,2,3,..,n} \right)$ ，统一定义曲线的次数为p，提取控制点、权重和节点向量。

2）估算单条曲线长度占整个曲线的占比，记为 $s{c_i}$ 。

3）将曲线 ${C_0}$ 参数区间设置为 $\left( {0,s{c_0}} \right)$ ， ${C_i}$ 参数区间设置为 $\left( {\displaystyle\sum\limits_{i = 0}^1 {} s{c_i},\displaystyle\sum\limits_{i = 0}^i {} s{c_i}} \right)$ 。

4）连接控制多边形的节点矢量，产生拟合曲线。

图1为基于NURBS样条的曲线拟合实例，节点矢量AB之间的直线与拟合后的曲线最大距离为0.325。

2 基于计算机辅助技术的船舶型线优化设计 2.1 船舶水动力-阻力特性研究

船舶型线的设计优劣直接影响船体在航行过程的阻力，为了准确分析舰船型线与阻力特性的关系，对船舶的水动力-阻力特性进行研究。

首先建立船舶水动力分析的基础理论方程如下：

1）连续性方程

$\frac{{{\rm{d}}{\rho_0}}}{{{\rm{d}}t}}+{\rho_0}\Delta \cdot V = 0 \text{，}$

式中： ${\ \rho _0}$ 为海水密度； $\Delta$ 为拉普拉斯参数。

2）雷诺方程

$\left\{ {\begin{array}{*{20}{l}} {{\rho _0}\dfrac{{{\rm{d}}{V_x}}}{{{\rm{d}}t}} = \dfrac{{\partial \sigma }}{{\partial x}} + {\rho _0}f} ，\\ {\dfrac{{\partial \rho {V_x}}}{{\partial t}} + \dfrac{{{\partial ^2}(P)}}{{\partial x}} = \dfrac{{\delta P}}{{\delta x}} + \dfrac{\partial }{{\partial {V^2}}}\left(\delta \dfrac{{\partial {V_y}}}{{\partial X}}\right) - Q} 。\end{array}} \right.$

式中： $V$ 为海水流动速度； $P$ 为静压力； $Q$ 为雷诺误差系数^[3]。

海水的流场速度势满足：

$\psi \left( {x,y} \right) = - kV + {\varphi _c} \text{，}$

式中， ${\varphi _c}$ 为海水的扰动势能，海水的流场满足下式：

${\varGamma ^2}\psi \left( {x,y} \right) = 0 。$

3）能量方程

${\rho _0}\frac{{{\rm{d}}E}}{{{\rm{d}}t}} = - {\rho _0}\Delta \cdot V + Q - \Delta q \text{。}$

式中： $Q$ 为流体的热能； $E$ 为流体的动能。

4）船舶运动建模

定义船舶运动坐标系的原点为重心位置处，OX轴与运动方向平行；OZ轴垂直于甲板平面，指向上方，OY轴指向船舶的左舷，建立船舶运动方程为：

$\left\{ {\begin{array}{*{20}{c}} {m\left( {u - rv} \right) = {M_x}}\text{，} \\ {m\left( {v - ru} \right) = {M_y}} \text{，}\\ {{J_x}r = {M_x} - {M_y}\cos \alpha } \text{。} \end{array}} \right.$

式中： $u$ ， $v$ 为运动速度； ${M_x}$ ， ${M_y}$ 外加转矩；m为船舶的质量。

船舶表面的流体-固体物面条件可写为：

$\frac{{{\partial }\psi }}{{\partial n}} - Vn = 0 \text{，}$

可得单位流体的垂向速度为：

${v_n} = \frac{{{k_1}{v_x} + {k_2}{v_y}}}{{\sqrt {{H_x}^2 + {H_y}^2} }} 。$

式中： ${v_x}$ ， ${v_y}$ 为单位流体的速度分量^[4]；H_x，H_y为动量分量。

最终得到船舶阻力方程为：

$F(X,Y,t) = A\cos \left( {\frac{{2\text{π} }}{\lambda }\left( {Y\cos \theta + X\sin \theta - {v_n}t} \right)} \right) 。$

式中： $\lambda$ 为波长； $\theta$ 为航向角。

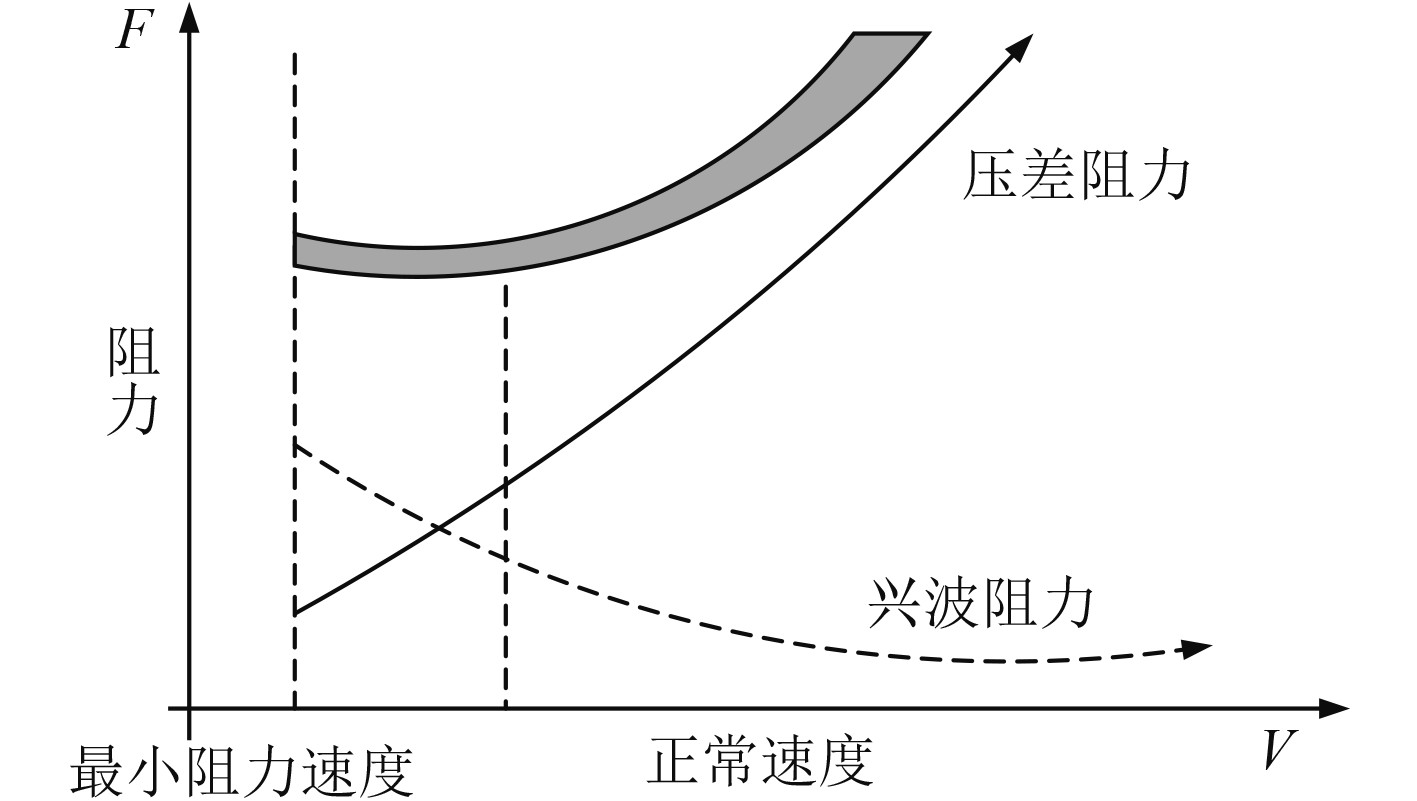
船舶航行速度与阻力之间的关系曲线如图2所示。

可知，随着航行速度的增加，兴波阻力逐渐下降，而压差阻力逐渐增加。

2.2 基于NURBS样条的船舶型线和曲线优化设计

基于NURBS样条进行船舶剖切面型线和船体曲面的优化。

1）船舶尾部剖切面型线

首先建立船舶主体尺寸的变换函数为：

$\begin{array}{*{20}{l}} {{X_t} = \lambda {X_O}} \text{，}\\ {{Y_t} = \beta {Y_O}} \text{，}\\ {{Z_t} = \gamma {Z_O}} \text{。} \end{array}$

式中： $\left( {{X_t},{Y_t},{Z_t}} \right)$ 为优化后尺寸边界的任一点坐标； $\left( {{X_o},{Y_o},{Z_o}} \right)$ 为优化前的尺寸边界的任一点坐标； $\lambda /\beta /\gamma$ 为尺寸变换系数。

在剖切面型线优化过程中^[5]，船舶主体尺寸的变换函数保持不变，建立剖切面的型线公式如下：

${f_P} = \left\{ {\begin{array}{*{20}{l}} {{R_1} = {k_i} \times {B_0}\sin {\alpha _1}} \text{，} \\ {{R_2} = \left( {y_d/2 - {k_t}} \right)\tan {\alpha _2} - {D_0}} 。\end{array}} \right.$

其中： ${k_i}$ 和 ${k_t}$ 分别为剖切线的比例系数； ${B_0}$ 为型宽； ${\alpha _1}$ 为尾部升角； ${\alpha _2}$ 为尾部外扩角； ${D_0}$ 为型深。

船舶尾部剖切面型线的数学模型如图3所示。

图中，R₁为船身中心线水上部分，R₂为壳体型线。

2）船舶曲面构造

船体曲面由无数曲线构成，首先基于NURBS样条建立船体型线的节点为：

${V_{i,j}}\left( {i = 0,1,...,m;j = 0,1,...,n} \right) \text{，}$

得到型线的节点方向矢量为：

$\begin{gathered} F = \{ \underbrace {0,{t_{p + 1}}, \cdots ,{t_n},1}_{p + 1}\}，\\ K = \{ \underbrace {0,{w_{q + 1}}, \cdots ,{w_n},1}_{q + 1}\} 。\\ \end{gathered}$

根据型线和节点矢量建立曲面如下：

$S(F,K) = \sum\limits_{i = 0}^n {\sum\limits_{j = 0}^n {{N_{i,p}}(F)} } {N_{j,p}}(K){V_{i,j}} 。$

式中， ${N_{j,p}}(K)$ 和 ${N_{i,p}}(F)$ 分别为NURBS样条函数。

2.3 基于NURBS样条型线设计的船舶阻力特性仿真分析

针对船舶型线优化前后的阻力特性，本文采用了CFD计算流体力学分析软件Fluent进行仿真，仿真的波浪载荷如下：

$f = {\varphi _0}\cos \left( {kx - {w_0}t} \right) 。$

其中： ${\varphi _0}$ 为波浪振幅； ${w_0}$ 为波浪频率；k为一个周期内的波数^[6]。

CFD仿真采用的边界参数如表1所示。

仿真得到船舶型线优化前A和优化后B的阻力特性如图4所示。

可知，经过船舶型线优化后的船舶仿真中，阻力特性有明显的降低。

3 结　语

船舶型线设计与船舶的流体动力学性能息息相关，本文基于NURBS样条进行船体型线的优化设计，同时结合计算流体力学（CFD）分析、有限元分析等工具，进行了型线优化的仿真分析。基于计算机辅助的船舶型线设计是一种高效、精确和可靠的设计方法，可以更好地设计和优化船舶的外形和型线，以满足船舶的性能和要求。