2. 赣南科技学院,江西 赣州 341000
2. Gannan University of Science and Technology, Ganzhou 341000, China
通信网络作为大规模舰船的数据传输通道,实现舰船与舰船、舰船与舰船管理部门的数据共享。舰船通信设备负责采集舰船通信数据,但因通信网络数据量巨大[1-2],通信协议不同等原因,导致数据传输过程中容易出现通信异常数据,直接影响大规模舰船通信数据传输效率,因此研究大规模舰船通信异常数据检测方法,可在短时间内识别大规模舰船通信异常数据。王晓湘等[3]研究通信异常数据检测方法,但该方法未对原始数据进行去噪处理,导致通信异常数据检测精度低。康颖等[4]提出Deep SVDD的通信异常数据检测方法,但该方法的模型训练过程会出现过于拟合问题,影响大规模舰船通信异常数据检测效果。
并行深度卷积神经网络算法的拟合能力较强[5],并在数据分类领域取得较好的应用效果。为了解决当前大规模舰船通信异常数据检测方法的局限性,设计基于并行深度卷积神经网络算法的大规模舰船通信异常数据检测方法,并通过具实验分析其性能。结果表明,本文方法可以提高大规模舰船通信异常数据检测效率,能够保障大规模舰船通信数据的安全。
1 大规模舰船通信异常数据检测 1.1 大规模舰船通信数据预处理采集大规模舰船通信数据过程中,容易受到噪声信号的干扰,导致数据中存在大量噪声,因此通过小波变换实施降噪处理,为后续大规模舰船通信异常数据检测奠定基础。通过离散化连续小波得出函数f(t),其变化公式如下:
| $ M{T_f}\left( {\alpha ,\beta } \right) = \int_R {f{{\left( t \right)}^{}}} {\varepsilon _{\alpha ,\beta }}\left( t \right){\rm{d}}t 。$ | (1) |
其中:α、β为参变量分别用;MTf(α,β)为小波变换系数;εα,β(t)为基小波。经伸缩和平移得出εα,β(t)表达式如下[5]:
| $ {\varepsilon _{\alpha ,\beta }}\left( t \right) = {2^{ - \frac{\alpha }{2}}}\varepsilon \left( {{2^{ - \alpha }}t - \beta } \right),$ | (2) |
当伸缩和平移得出基小波,此时该基小波符合小波紧框架条件时,离散小波变换逆变换表达如下:
| $ f\left( t \right) = \sum\limits_{\alpha ,\beta } {\left\langle {f,{\varepsilon _{\alpha ,\beta }}} \right\rangle {{\tilde \varepsilon }_{\alpha ,\beta }}\left( t \right)} = \frac{1}{C}\sum\limits_{\alpha ,\beta } {M{T_f}} \left( {\alpha ,\beta } \right){\varepsilon _{\alpha ,\beta }}\left( t \right) 。$ | (3) |
其中,C为常量。
通过阈值电平选取合适阈值,提升小波变换对大规模舰船通信数据降噪的效果。若设置阈值电平用
| $ {\hat \lambda _\alpha } = \left\{ \begin{gathered} 0,\mathop {}\nolimits^{} \left| {{\lambda _\alpha }} \right| < B ,\\ {\lambda _\alpha }{,^{}}^{}\left| {{\lambda _\alpha }} \right| \geqslant B,\\ \end{gathered} \right. $ | (4) |
软阈值可过滤掉对大规模舰船通信数据检测中不重要的系数,软阈值表达式如下:
| $ {\hat \lambda _\alpha } = \left\{ \begin{array}{ll} 0,& \left| {{\lambda _\alpha } < B} \right| ,\\ {{\rm{sgn}}} \left( {{\lambda _\alpha }} \right)\left( {\left| {{\lambda _\alpha }} \right| - B} \right),& \left| {{\lambda _\alpha } \geqslant B} \right| 。\end{array} \right. $ | (5) |
其中,sgn()为符号函数。
一般阈值公式如下:
| $ A = \sqrt {2 \times \lg \left( \kappa \right)\varphi }。$ | (6) |
其中:噪声强度用
利用小波变换对大规模舰船通信数据实施降噪处理的具体步骤如下:
1)分解环节,通过小波对采集的大规模舰船通信数据实施N层小波分解;
2)阈值处理环节,依据分解后每层小波系数选取1个阈值,同时对该系数进行软阈值处理;
3)重构环节,利用小波重构实现对原始大规模舰船通信数据降噪。
1.2 舰船通信异常数据检测并行深度卷积神经网络是以2个深度CNN为基础,包括CNN数据变换流和原Alex-Net数据变换流,将经过小波去噪后的大规模舰船通信数据作为并行深度卷积神经网络的2条变换流输入,通过并行深度卷积神经网络的训练,通过交叉混合,提取舰船通信异常数据特征,实现大规模舰船通信异常数据检测。深度CNN结构如图1所示。

|
图 1 深度CNN结构图 Fig. 1 Deep CNN structure diagram |
由图1可知,深度CNN包括输入层、卷积层、池化层、全连接层等组成[6]。其中,卷积层负责提取特征,第L层卷积运算公式如下:
| $ {E_{i,L}} = {d_{j,L}} + \sum\limits_i {{E_{i,L - 1}}} \times {S_{ij,L - 1}}。$ | (7) |
其中:Sij,L−1为卷积核;Ei,L为第i个神经元输入;dj,L为第j个神经元偏置。
利用激活函数可提高网络收敛速度,一般采用ReLU激活函数,其表达式如下:
| $ f\left( x \right) = {\rm{MAX}}\left( {0,x} \right) ,$ | (8) |
全连接层负责与池化层相连,其公式为:
| $ {K_{j,L}} = {d_{j,L}} + \sum\limits_i {{\omega _{ij,L}}} {x_{i,L - 1}}。$ | (9) |
其中:xi,L−1为第L−1层特征值;ωij,L为神经元权重;Kj,L为第j个神经元输入。
分类层利用Softmax分类函数对输出的预测结果实施分类。Softmax分类函数表达式如下:
| $ \gamma \left( {{K_{j,L}};\vartheta } \right) = {e^{\vartheta _j^\varGamma{x_{i,L}}}}/\sum\limits_{L = 1}^\varpi {{e^{\vartheta _j^\varGamma {x_{i,L}}}}} ,$ | (10) |
其中:
采用并行深度卷积神经网络实现大规模舰船通信异常数据检测,在模型训练过程中,前向传播负责提取大规模舰船通信异常数据特征,反向传播负责修正误差。并行深度卷积神经网络包括5个卷积层、3个池化层、3个全连接层的2个深度CNN。hL为设置变换函数,ωL为权值矩阵,XL为上一层输出值,在前向传播训练过程中,输出函数表达式如下:
| $ q = {h_L}\left( {{X_L};{\omega _L}} \right) ,$ | (11) |
在并行深度卷积神经网络通过log-loss误差函数与Softmax回归函数计算输出结果的误差。在第L层,损失函数公式如下:
| $ \iota \left( {{x_i},{z_i}} \right) = \eta \sum\limits_{k = 1}^L {} \sum\limits_{k = 1}^L {} {\left\| {{\omega _j}} \right\|^2} + \left[ { - \frac{1}{n}\sum\limits_{i = 1}^n {\left( {{z_i} - \left( {{x_i};{\omega _i}} \right)} \right)} } \right] 。$ | (12) |
其中:n为样本总数;
目标函数表达式如下:
| $ R = {\arg _{{\omega _L}}}\min {\raise0.7ex\hbox{$1$} \mathord{\left/ {\vphantom {1 n}}\right.} \lower0.7ex\hbox{$n$}}\sum\limits_{i = 1}^n {\iota \left( {{h_L}\left( {{x_i};{\omega _L}} \right),{z_i}} \right)},$ | (13) |
采用式(14)对权值矩阵实施更新,具体为:
| $ \frac{{\partial \iota }}{{\partial {\omega _L}}} = \eta {\omega _L} + {h'_L}\left( {{X_L};{\omega _L}} \right) \times \left[ {\left( { - {\raise0.7ex\hbox{$1$} \mathord{\left/ {\vphantom {1 n}}\right.} \lower0.7ex\hbox{$n$}}} \right)\left( {{Z_L} - {h_L}\left( {{X_L};{\omega _L}} \right)} \right)} \right]。$ | (14) |
利用式(14)实施迭代得出最优目标函数。通过链式求导法更新2个全连接层的权值,当卷积层下层为降采样层,卷积层误差求解公式如下:
| $ \vartheta _{L - 1}^j = {\rm{upsample}}\left( {\vartheta _L^j} \right) \cdot {h'_L}\left( {x_L^j;{\omega _L}} \right)。$ | (15) |
其中:
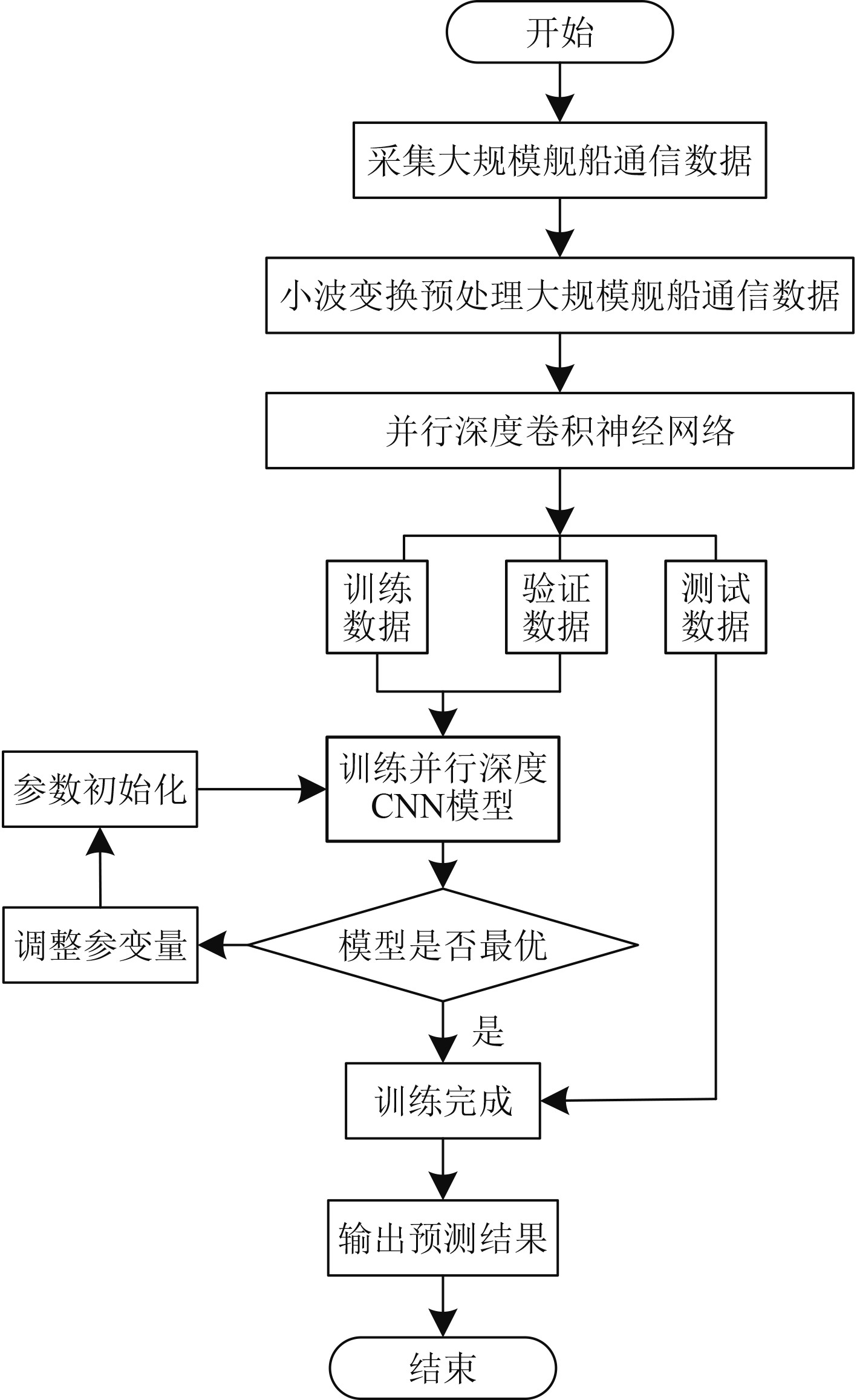
基于并行深度卷积神经网络算法的舰船通信异常数据检测流程如图2所示。
|
图 2 大规模舰船通信异常数据检测流程 Fig. 2 Detection process for abnormal data in large-scale ship communication |
由图2可知,并行深度卷积神经网络算法的大规模舰船通信异常数据检测流程如下:
1)利用舰艇通信设备采集大规模舰船通信数据;
2)采用小波变换对采集大规模舰船通信数据实施降噪处理;
3)将降噪后的大规模舰船通信数据作为并行深度卷积神经网络的输入;
4)将经过预处理的大规模舰船通信数据集划分为测试集、验证集、训练集;
5)模型训练,采用并行的2个深度CNN,分别将卷积变换步长设置为4和6,提取舰船通信数据特征,提升特征提取的鲁棒性,全连接层位于变换流的上面,实施对2条变换流提取CNN特征经过2次交叉处理得出特征向量集,采用Softmax分类函数得出舰船通信异常数据特征;
6)输出训练分类结果,即舰船通信异常数据检测结果。
2 性能分析实验对象为某大规模舰船通信数据集,见表1。将本文方法检测大规模舰船通信异常数据,测试本文方法的应用效果。
|
|
表 1 实验数据集 Tab.1 Experimental Dataset |
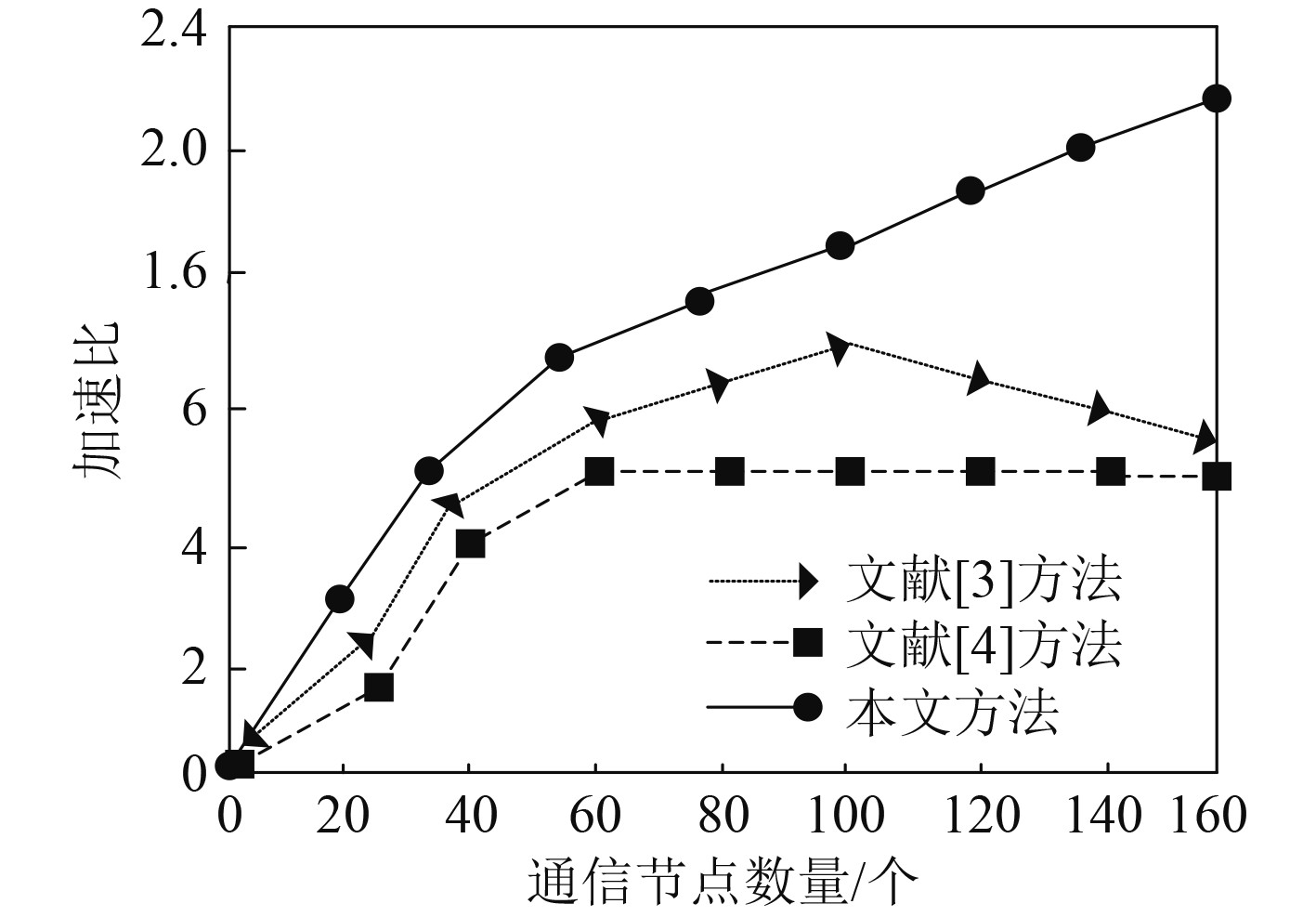
实验对比方法分别为文献[3]LSTM的通信异常数据检测方法、文献[4]Deep SVDD的通信异常数据检测方法,分别采用3种方法对大规模舰船通信异常数据进行检测,得出3种方法的加速比如图3所示。可知,本文方法的加速比明显高于文献[3]方法、文献[4]方法的性能。随着通信节点数量的增加,本文方法的加速比呈上升趋势。而文献[3]方法在通信节点数量为60个以后,加速比呈现稳定趋势,其加速始终为5;文献[4]方法在通信节点数量大于100个时,文献[4]方法的加速比呈下降趋势。经对比分析表明本文方法的并行化效果最佳,检测大规模舰船通信数据集能力最强。
|
图 3 三种方法的加速比 Fig. 3 Acceleration ratios of three methods |
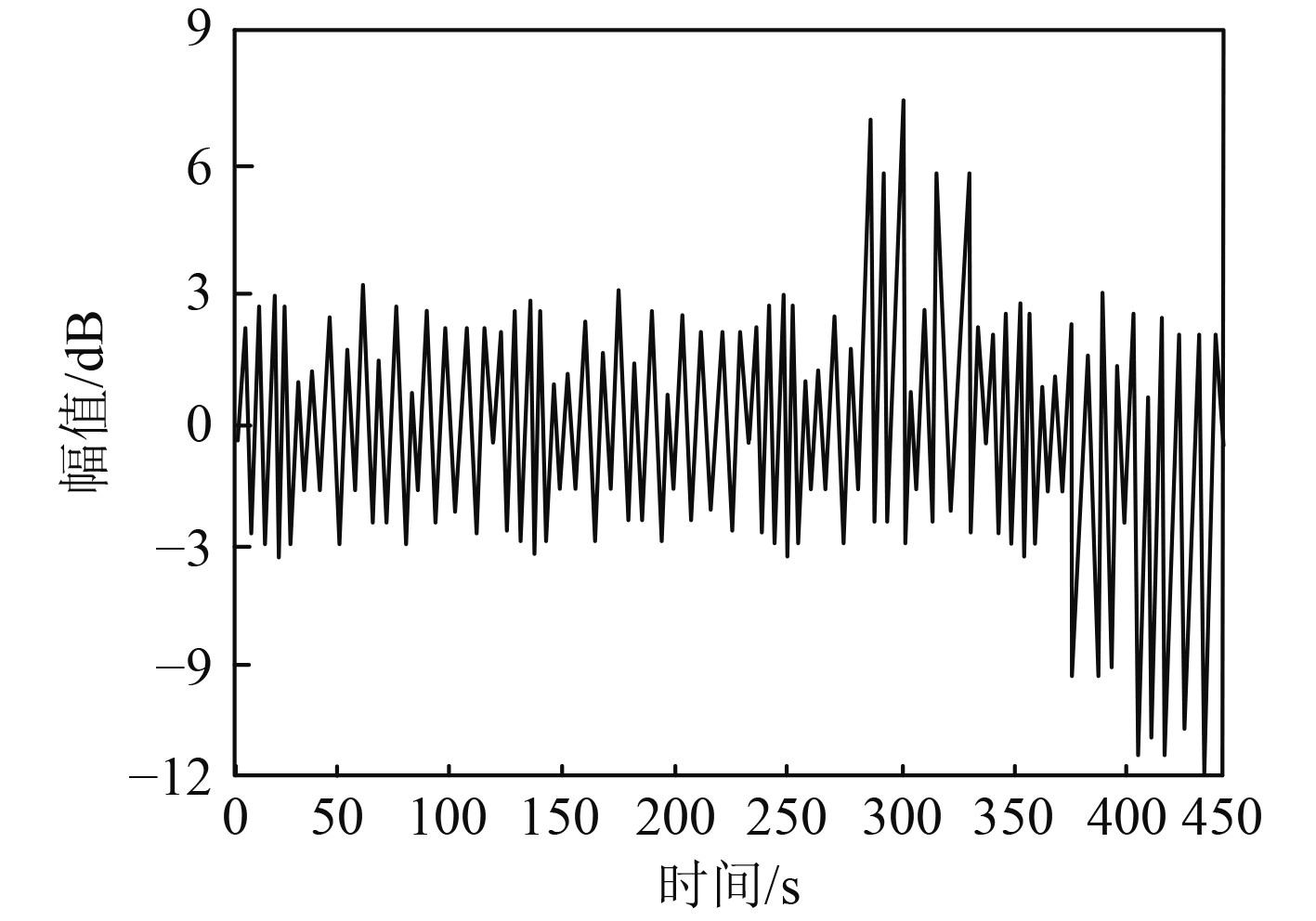
因采集大规模舰船通信数据中存在大量噪声,采用小波变换对舰艇通信设备采集大规模舰船通信数据实施降噪处理,得出降噪后大规模舰船通信数据,结果如图4所示。可知,采用小波变换可有效去除大规模舰船通信数据中噪声,挖掘出噪声覆盖下的真实大规模舰船通信数据,为大规模舰船通信数据检测提供准确的数据来源。
|
图 4 去噪后大规模舰船通信数据 Fig. 4 Large scale ship communication data after denoising |
将降噪后数据输入并行深度卷积神经网络中得出大规模舰船通信异常数据检测结果,选取误报率、准确率作为测试方法的性能指标,测试结果见表2。分析表2可知,采用本文方法对大规模舰船通信异常数据进行检测,综合这些指标结果表明,本文方法可有效实现大规模舰船通信异常数据和正常数据检测,适应性强,且检测精度高。
|
|
表 2 本文方法的大船通信异常数据检测结果 Tab.2 Detection results of abnormal communication data for large ships using the method in this article |
针对大规模舰船通信异常数据检测难度大的问题,提出基于并行深度卷积神经网络算法的大规模舰船通信异常数据检测方法,以提高大规模舰船通信异常数据检测能力。实验结果表明:本文方法采用小波变换可有效去除大规模舰船通信数据中噪声,其应用效果较好;可有效实现大规模舰船通信异常数据和正常数据检测,具有较强的适应性,获得了高精度的大规模舰船通信异常数据检测结果。
| [1] |
张艺严, 马巍, 李彬. 能量受限无人机与移动舰船通信中的轨迹优化[J]. 中国舰船研究, 2022, 17(4): 47-56. DOI:10.19693/j.issn.1673-3185.02764 |
| [2] |
彭旭, 饶元, 乔焰. 基于宽度卷积神经网络的异常农情数据检测方法[J]. 华南农业大学学报, 2022, 43(2): 113-121. DOI:10.7671/j.issn.1001-411X.202103050 |
| [3] |
王晓湘, 刘洞天, 刘南江, 等. 基于LSTM的震后通信数据异常检测分析[J]. 中国地震, 2022, 38(2): 270-279. |
| [4] |
康颖, 赵治华, 吴灏等. 基于Deep SVDD的通信信号异常检测方法[J]. 系统工程与电子技术, 2022, 44(7): 2319-2328. |
| [5] |
唐佩, 李青锋, 朱川曲, 等. 基于小波变换的微震阈值去噪方法[J]. 湖南科技大学学报(自然科学版), 2021, 36(4): 1-7. DOI:10.13582/j.cnki.1672-9102.2021.04.001 |
| [6] |
胡健, 龚克, 毛伊敏, 等. 基于Im2col的并行深度卷积神经网络优化算法[J]. 计算机应用研究, 2022, 39(10): 2950-2956+2961. DOI:10.19734/j.issn.1001-3695.2022.03.0114 |
 2023, Vol. 45
2023, Vol. 45
