舰船通信网络运行时,发射机与接收机同时工作时,容易受到众多因素的干扰[1]。网络信道容易受到发射机和接收机的相对运动、海浪阴影效应以及气象环境等众多因素影响[2],舰船通信网络信号变化呈现明显的动态性。构建舰船通信网络信号动态变化特性的数学模型,利用所构建的数学模型,确定舰船通信网络的信号变化情况,是海上无线通信信道研究的重点[3]。利用舰船通信网络信号动态变化特性数学模型,确定舰船通信网络发送端、接收端的接收功率,以及不同传输距离时信号的关系,是提升舰船通信网络通信质量的重要基础。
目前已有众多学者针对舰船通信网络的通信性能进行研究。刘琪等[4]针对舰船通信网络受方磁场影响的信号重构进行研究,确定了信号换算方法。该方法确定了舰船通信网络频率与能量谱之间的关系,大采样间隔时,通过信号重构提升舰船的通信水平。徐茂等[5]利用卷积神经网络对舰船通信网络信号的时频特征进行调制识别,该方法采集大量的调制信号,对调制信号的时频特征进行傅里叶变换提取信号特征,所提取特征输入卷积神经网络,利用卷积神经网络实现信号的调制识别,通过信号调制识别结果,提升通信网络的通信质量。以上方法虽然针对通信网络的通信性能进行研究,但是并未考虑舰船通信网络受干扰时,信号的动态变化特性,无法全面体现舰船通信网络的通信性能[6]。
针对以上方法在舰船通信网络研究中存在的问题,本文构建舰船通信网络信号动态变化特性数学模型,明确舰船通信网络运行时,其信号存在的动态变化特性,为提升舰船通信网络的通信质量提供可靠依据。
1 网络信号动态变化特性数学模型 1.1 舰船通信网络的信道模型用
| $ R = {\log _2}\left( {1 + \frac{S}{{N + I}}} \right) 。$ | (1) |
式中:
舰船通信网络中,网络噪声一直存在。提升发射机的发射功率,以及降低节点受其他节点干扰的功率,是提升信道容量的重要方式。分析节点受其他节点影响的信道干扰,具有一定必要性。设存在
节点空间
| $ E\left[ {\exp \left( {z\sum } \right)} \right] = \exp \left\{ {\int\limits_R {\left[ {\exp \left( {zf\left( x \right)} \right) - 1} \right]} } \right\} 。$ | (2) |
通过坎贝尔定理,明确舰船通信网络中由于节点形成的干扰。利用泊松点过程,构建舰船通信网络的信道模型,具有较高的可行性。
1.2 舰船通信网络的信道衰落模型舰船通信网络除受到节点干扰外,同时受到环境干扰,网络信道存在大尺度衰落。通过信道衰落模型,体现舰船通信网络的信道衰落变化。造成舰船通信网络信道衰落主要原因为:传输距离形成的路径损耗;障碍物形成的阴影衰落;受海浪、通信发射机与通信接收机运动影响。舰船通信网络信道的小尺度衰落存在明显的随机性。充分考虑造成信道衰落的原因,用
| $ L\left( d \right) = \lg \frac{{2{\text{π}} d\beta }}{c} - {G_t} - {G_r}。$ | (3) |
式中:Gr与Gt分别为接收机与发射机的天线增益,β与
Friis公式构建的是舰船通信网络在理想环境下的信道衰落情况。舰船通信网络实际运行时,存在众多干扰条件,需要进行如下改进:
1)直射路径的信道衰落
舰船通信网络的应用环境中,存在海上的大气传输损耗、考虑大气影响,构建舰船通信网络信道直射路径的信道衰落模型表达式如下:
| $ {L_1}\left( d \right) = k\lg \frac{{2{\text{π}} \beta d}}{c} - {G_t} - {G_r}。$ | (4) |
式中,
2)镜面反射路径的信道衰落
舰船通信网络应用时,需要考虑海洋表面的反射损耗、稀疏信道路径损耗以及浪面反射影响造成的衰落效应。引入漫反射路径、镜面反射路径以及直射路径于信道衰落模型中。舰船通信网络受海洋表面反射路径影响,反射损耗的表达式如下:
| $ \varepsilon = \lg \left( {\frac{{U_H^2 + U_V^2}}{2}} \right)。$ | (5) |
式中:UH与UV分别为水平极化波以及垂直极化波的反射系数,其表达式为:
| $ {U_H} = \frac{{\sin \theta - \sqrt {\eta - {{\cos }^2}\theta } }}{{\sin \theta + \sqrt {\eta - {{\cos }^2}\theta } }},$ | (6) |
| $ {U_V} = \frac{{\eta \sin \theta - \sqrt {\eta - {{\cos }^2}\theta } }}{{\eta \sin \theta + \sqrt {\eta - {{\cos }^2}\theta } }}。$ | (7) |
式中:
入射角
| $ \theta = \frac{{\text{π}} }{2} - \arcsin \frac{{{h_t} + {h_r}}}{{{d_{SR}}}}。$ | (8) |
式中:ht与hr分别为发射机与接收机的天线高度;dSR为镜面反射路径长度。
选取直射路径与反射路径的到达时延
| $ {d_{SR}} = \frac{{2{h_t}{h_r}}}{{c\tau }} + \frac{{c\tau }}{2},$ | (9) |
综合以上过程,构建镜面反射路径的信道衰落表达式如下:
| $ {L_{SR}}\left( d \right) = \frac{{\lg 4{\text{π}} Adk\beta \varepsilon + t}}{{c\omega }}{\sin ^2}\phi - {G_t} - {G_r}。$ | (10) |
式中:
3)漫反射路径信道衰落
漫反射路径与镜面反射路径的功率之比,满足高斯分布。依据高斯分布,构建漫反射路径的信道衰落表达式如下:
| $ {L_{DR}}\left( d \right) = \frac{{\lg 4{\text{π}} Adk\beta \varepsilon + t}}{{c\omega }}{\sin ^2}\left( {\chi \gamma /\sigma } \right) - {G_t} - {G_r} 。$ | (11) |
式中:
通过以上过程,构建舰船通信网络的信道衰落模型,实现舰船通信网络信道衰落估计参数解耦。
1.3 基于马尔科夫链的信号动态变化特性数学模型利用高斯模型描述舰船通信网络的恒参信道。设全部带宽下,功率谱密度为常数。舰船通信网络接收信号包络的概率密度函数表达式如下:
| $ P\left( x \right) = \frac{1}{{\sqrt {2{\text{π}} } \delta }}\exp \left( { - \frac{{{x^2}}}{{2{\delta ^2}}}} \right) ,$ | (12) |
式中,δ2与
舰船通信网络信号传输时,具有动态特性,存在信号缺失情况。舰船通信网络信号动态变化特性利用误码率衡量,对舰船通信网络信号调制后,通信网络信道的误码率表达式如下:
| $ Q = \frac{1}{{\sqrt {2\varPsi } }}\exp {\left( { - \varPsi } \right)^2}。$ | (13) |
式中,
舰船通信网络信号传输时,存在时变特性以及随机特性,利用马尔科夫链体现舰船通信网络的信号动态变化特性。马尔科夫链指信号传输的离散时间随机过程。该过程指满足一定条件时,信号的未来状态,仅与信号当前状态相关,与其他时间的信号无关。马尔科夫链模型中,信号伴随时间的变化,依据概率分布实现状态的动态变化。
P表示舰船通信网络信号动态变化特性的状态转移矩阵,该矩阵与信号的动态变化相关,矩阵内的元素表示信号变化状态的概率。用
结合平顶高斯函数与蒙特卡罗统计方法,构建舰船通信网络的信号传输表达式如下:
| $ f\left( x \right) = \exp \left( { - \frac{{\left( {N + 1} \right){x^2}}}{{{b^2}}}} \right)\sum\limits_{k = 0}^N {\frac{1}{k}} {\left( {\frac{{\left( {N + 1} \right){x^2}}}{{{b^2}}}} \right)^k} 。$ | (14) |
式中:
依据网络信号传输状态,考虑信道衰落情况,构建信号传输距离、接收机的接收功率、信号接收位置的二维传输模型表达式如下:
| $ f\left( {d,x} \right) = {\xi _1}\left( d \right) + {\xi _2}\left( d \right) + L\left( d \right)\exp \left( { - \frac{{3{x^2}}}{{{\xi _3}{{\left( d \right)}^2}}}} \right) 。$ | (15) |
式中:f(d,x)为信号接收功率与初始功率的差值;
为了测试所研究数学模型,选取舰船通信基站作为舰船通信网络的中心,分析舰船通信网络的信号动态变化特性。舰船通信网络的发射机设置于海上智能通信基站内,接收机设置于舰船内。舰船在海面上以12 km/h的速度前进,通信网络采样间隔为10 s。舰船通信网络运行时,发射信号与接收信号结果如图1所示。可知,本文模型可以有效模拟舰船通信网络的信号变化,舰船通信网络伴随环境变化,存在信号衰落等情况。
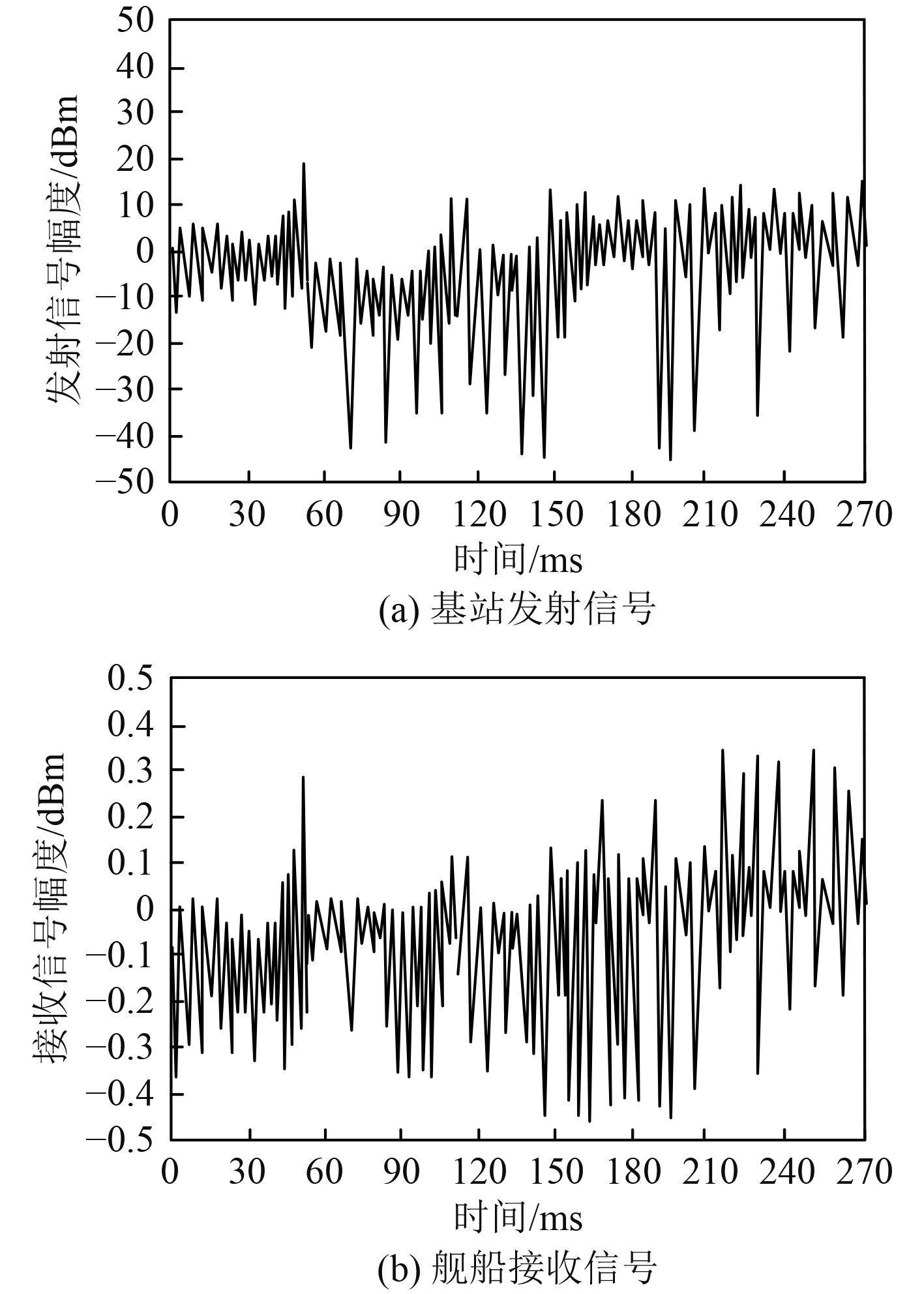
|
图 1 舰船通信网络仿真结果 Fig. 1 Simulation results of ship communication network |
统计采用本文模型模拟舰船通信网络的通信状态,舰船不同运动条件下,舰船通信网络的信道衰落情况,统计结果如图2所示。可以看出,本文针对舰船通信网络构建的数学模型,有效体现舰船通信网络信号的动态变化,直观衡量舰船通信网络的信道衰落情况,展示舰船通信网络在舰船为不同运动状态时的动态变化特性。
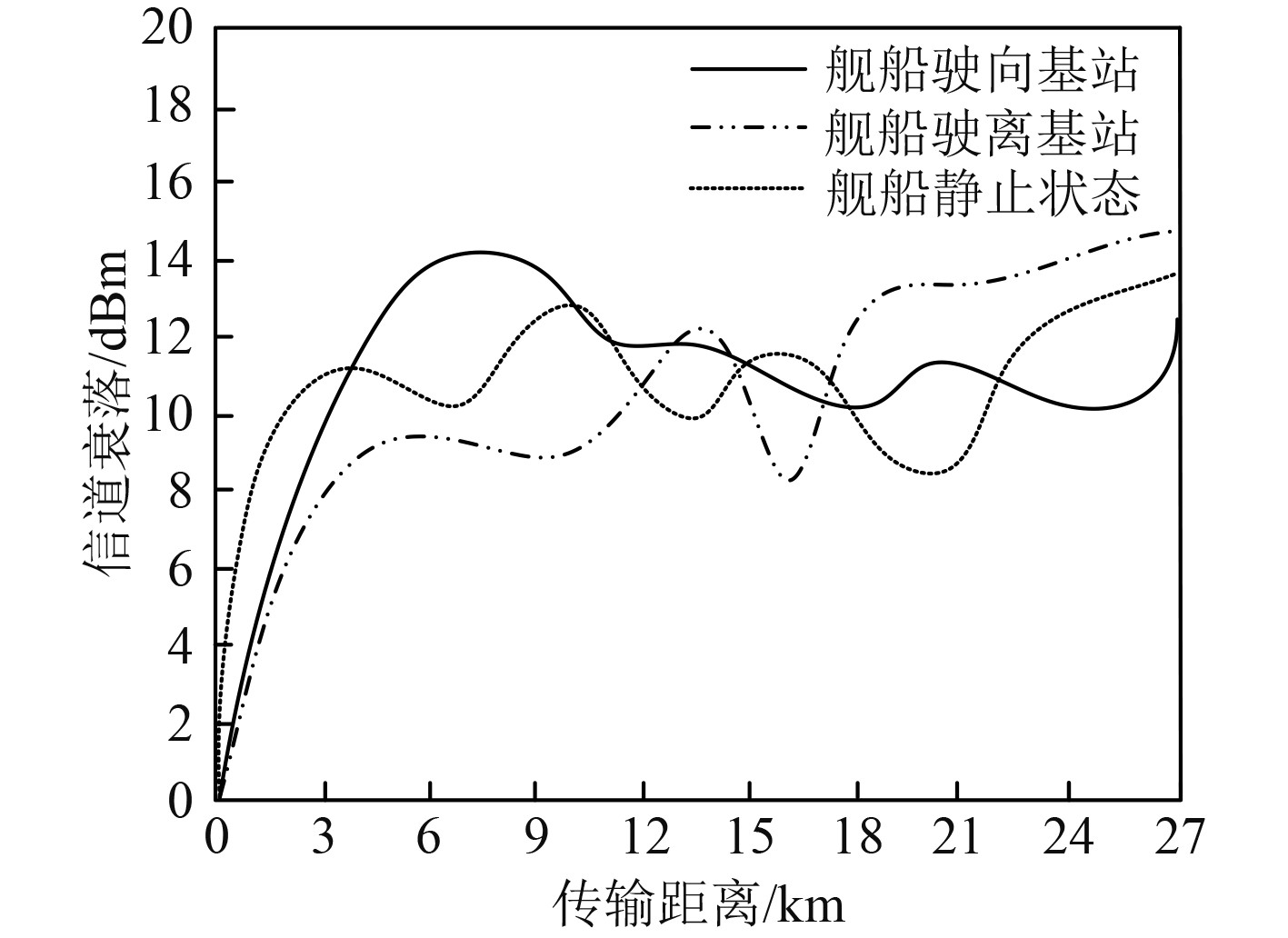
|
图 2 舰船通信网络信道衰落 Fig. 2 Channel fading of ship communication network |
统计海洋风速为5 m/s、10 m/s以及15 m/s时,不同通信距离时的网络误码率变化,统计结果如图3所示。可知,伴随舰船通信网络传输距离的不断增加,舰船通信网络的误码率不断提升。伴随传输距离的不断增加,网络信号存在丢失与衰落等情况,提升了网络信号传输的误码率。通信基站与舰船之间的距离的增加,平均误码率呈现上升趋势。风速增加时,舰船通信网络所处的环境更加复杂,随机性增加,平均误码率提升幅度更加明显。由于风力增大,海浪起伏的幅度更加明显,容易造成舰船倾斜等情况,影响舰船通信网络的通信性能,本文有效构建舰船通信网络信号动态变化特性的数学模型,应用性较强。
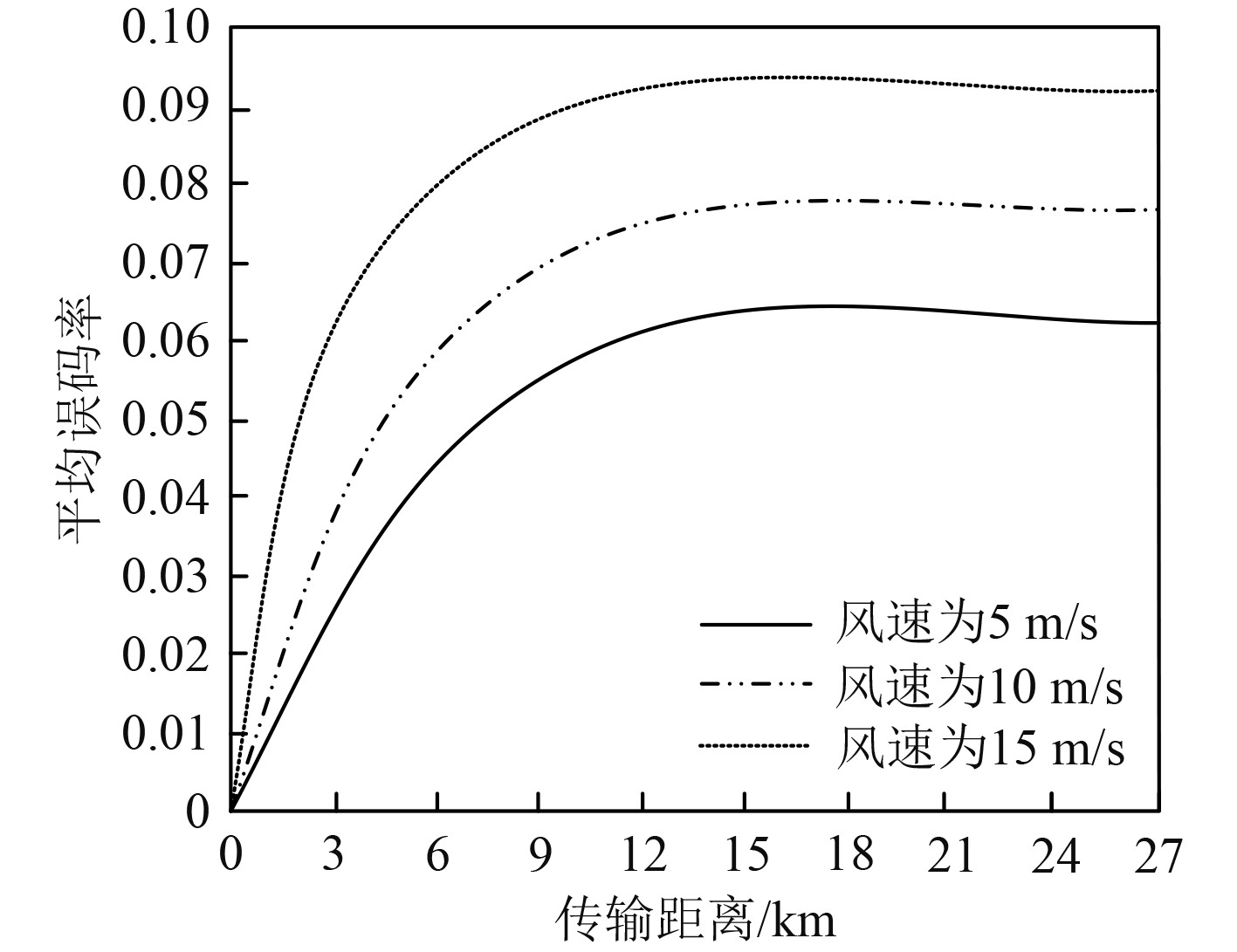
|
图 3 舰船通信网络误码率变化 Fig. 3 Changes in bit error rate of ship communication network |
舰船通信网络的应用环境复杂,构建舰船通信网络信号动态变化特性数学模型,准确地表征舰船通信无线信道变化,明确网络信号变化。所构建的数学模型,可以精确表现信道衰落情况。实验表明,所设计的数学模型可以对海上不同信道环境进行仿真,动态模拟舰船通信状态,具有较好的适应性,为动态环境下,舰船通信网络的通信性能提升提供基础。
| [1] |
秦博伟, 蒋磊, 郑万泽, 等. 基于半监督生成对抗网络的通信信号调制识别算法[J]. 空军工程大学学报(自然科学版), 2021, 22(5): 75-81. QIN Bo-wei, JIANG Lei, ZHENG Wan-ze, et al. A Communication Signal Modulation Recognition Algorithm Based on Semi-Supervised Generative Adversarial Networks[J]. Journal of Air Force Engineering University, 2021, 22(5): 75-81. |
| [2] |
张艺严, 马巍, 李彬. 能量受限无人机与移动舰船通信中的轨迹优化[J]. 中国舰船研究, 2022, 17(4): 47-56. ZHANG Yi-yan, MA Wei, LI Bin. Trajectory optimization for communication between energy-constrained UAV and moving ship[J]. Chinese Journal of Ship Research, 2022, 17(4): 47-56. |
| [3] |
李理, 李向欣, 殷敬伟. 基于生成对抗网络的舰船辐射噪声分类方法研究[J]. 电子与信息学报, 2022, 44(6): 1974-1983. |
| [4] |
刘琪, 孙兆龙, 姜润翔, 等. 一种舰船下方磁场的信号重构及换算方法[J]. 电工技术学报, 2022, 37(15): 3723-3732. |
| [5] |
徐茂, 侯进, 吴佩军, 等. 基于通信信号时频特性的卷积神经网络调制识别[J]. 计算机科学, 2020, 47(2): 175-179. DOI:10.11896/jsjkx.181202361 |
| [6] |
王晓惠, 冯彩英. 基于子波变换的无线通信网络干扰信号检测研究[J]. 激光与红外, 2022, 52(6): 875-880. |
 2023, Vol. 45
2023, Vol. 45
