2. 武汉船舶通信研究所,湖北 武汉 430079
2. The 722 Research Institute of CSSC, Wuhan 430079, China
在海上通信中遇到的一个重要问题就是抗干扰问题。随着通信事业的迅速发展,各类通信网的建立,使得有限的频率资源更加拥挤,相互之间的干扰更为严重,防止和降低这种相互之间的干扰,成为一大难题。跳频通信具有良好的抗干扰性,低截获概率及组网能力,因此跳频技术一出现,便在海上无线通信领域得到了很大的发展[1-2]。
为了对付包括跟踪式干扰在内的多种干扰方式,各国都在力图提高跳频速度。20世纪80年代常规跳频速度一般在200跳/秒左右,目前跳速基本要求在2000跳/秒以上。美国的军事星和舰队通信卫星7号和8号上装有的极高频(EHF)组件,上下行均使用了跳频技术,美军使用的Milsta和AFSATCOM系统也用了跳频技术,其中Milstar22系统跳频速率可以达到10000跳/秒,获得大于40 dB的扩频处理增益。美国研制的短波高速跳频电台CHESS,跳速为5000跳/秒,新一代的美国联合战术信息分系统JTIDS其跳频速率达到38000跳/秒[3]。但是目前国内对于高速跳频的研究仍处于初步阶段。
本文设计一种适用于海上通信的高速跳频通信同步方法,并通过Matlab进行了仿真,证明本方案的可行性与高效性,能够满足宽带高速跳频通信的需求,具备良好的应用价值。
1 概 述海上无线通信技术的发展在建设海洋强国的过程中发挥着至关重要的作用。然而,不同于地面无线通信系统,海上通信节点相对较少且分散,海上节点间通信距离通常较远,空间内分布较稀疏。因此,海上通信系统中抗干扰抗截获显得极为重要。对于我国而言,当前海上通信系统大多依赖国外技术,在无线传输中抗干扰、抗截获掌握的核心技术较少[4]。
海上无线传输中,由于通信距离远、信道衰落、以及各种干扰等因素影响,接收机的接收信号功率不是恒定的,而是有一个较大的变化范围[5]。即使接收机前端设计了自动增益控制模块,但由于其精度有限,在基带信号处理定时同步流程中也无法做到设置固定门限阈值[6]。使用各类恒虚警(Constant False Alarm Rate,CFAR)算法能够根据外界强度变化,自动调整门限,使同步的虚警概率基本保持不变[7]。但是该算法运算量较大,消耗硬件存储容量较多,在高速信号处理中实现难度较大。
本文提出一种海上通信宽带高速跳频同步方法,设计了定时粗同步和定时精同步两级处理。既简化了运算,又能够实现高精度的定时同步,为后续技术应用奠定基础。
2 高速信息粗同步方案在跳频信息传输中,同步主要有定时同步和跳频同步,其中定时同步包括前导信号设计和同步方案的原理,从这两部分介绍同步方案。
2.1 前导信号设计本方案设计中,定时同步包括帧同步和符号同步(码元同步),即从接收信号中确定信号帧的起止时刻和码元的起止时刻,为后续信号处理流程提供时间基准;载波同步是从接收信号中提取和恢复出与频偏载波同频同相的相干载波,以补偿接收信号的多普勒频偏,便于后续解调解码。图1为同步处理流程框图,输入数据是经过A/D中频采样并经过数字下变频和匹配滤波后的数字信号,该信号依次经过帧同步、符号同步和载波同步,送入下一级信号处理。

|
图 1 同步处理框图 Fig. 1 Block diagrams are processed synchronously |
同步算法基于伪随机序列即m序列,放置在帧首部作为信号帧的同步前导。为提高同步抗干扰性能,同步前导
| $ S_{9 p x c}(n)=a(n) e^{j {\text{π}} / 4}, a(n) \in\{-1,+1\} 。$ |
其中,
将同步前导中的每一个符号与其后一个符号做共轭相乘,得到一组新的序列,表达式为:
| $ \begin{aligned} \Delta s_{\text {sync }}(n) =& {{\rm{con}}}j\left[S_{\rm{gnx}}(n)\right] \cdot S_{\rm{gynx}}(n+1) =\\ & a(n) e^{-j {\text{π}} / 4} \cdot a(n+1) e^{j {\text{π}} / 4} = \\ &a(n) \cdot a(n+1)。\end{aligned} $ |
可以看到,新序列的取值变换成简单的+1和-1,取值与调制方式的相位选择无关。将该序列存在本地作为已知序列备用。
在接收端,信号经过无线信道(只考虑多普勒频谱,暂不考虑噪声),表达式为:
| $ r(n)=A a(n) e^{j {\text{π}}/ 4+j \omega n+j \varphi}, a(n) \in\{-1,+1\} 。$ |
其中:A是接收幅度;
| $ \begin{aligned} \Delta r(n) =&\operatorname{con} j[r(n)]-r(n+1) =\\ & A a(n) e^{-(j m / 4+j \omega n+j \varphi)}-A a(n+1) e^{j m / 4+j \omega(n+1)+j \varphi}= \\ & A^{2} a(n)-a(n+1) e^{j \omega}。\end{aligned} $ |
该序列与本地序列
| $\begin{aligned} corr(m) = &\sum\limits_{n = 1}^{N - 1} {\Delta {S_{sync}}(n) \cdot conj\left[ {\Delta r(n)} \right]} =\\ & \sum\limits_{n = 1}^{N - 1} {{A^2}{a^2}(n) \cdot {a^2}(n + 1){e^{ - j\omega }}} 。\end{aligned}$ |
当
| $ {corr}(\max )=A^{2}(N-1)。$ |
此即同步位置。
3 高速跳频同步详细设计 3.1 跳频设计考虑到波形的抗干扰性能与硬件实现能力,高可靠数据信息传输信号采用40000跳/秒的高速跳频方案。
系统跳频同步采用“快发慢收”方案,即发射端同步头采用40000跳/秒的高速跳频,接收端在跳频同步前,采用低速跳频搜索,增加跳频捕获的驻留时间。当接收端成功捕获跳频同步头后,获取准确的定时信息,并跟踪后续跳频图案,完成后续的跳频数据解调。
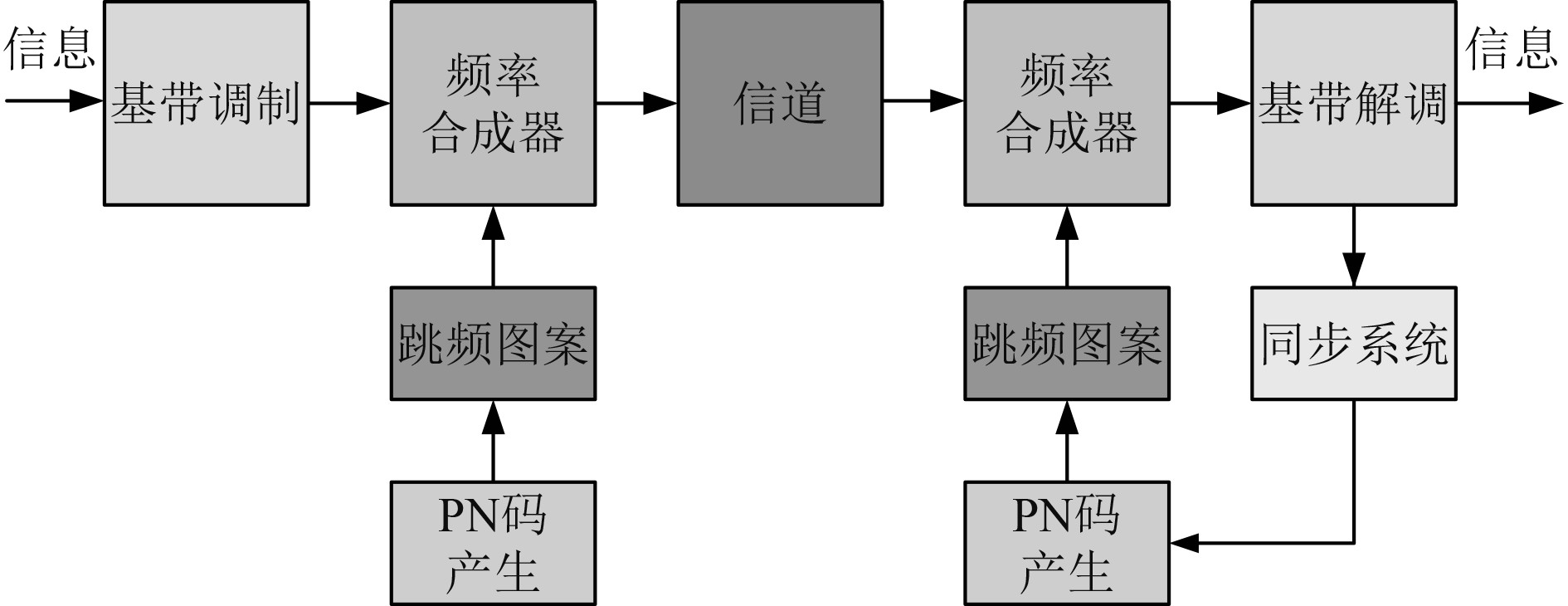
跳频通信系统的工作原理如图2所示。在发端用加密后的伪随机序列进行频移键控调制,使载波频率不停跳变,在收端用相同序列对信号进行恢复。从时域上看,跳频信号是一个多频率的频移键控信号,从频域上看,跳频信号在很宽的频带上以不等间隔随机跳变。
|
图 2 跳频通信系统工作原理图 Fig. 2 Schematic diagram of the operation of the frequency hopping communication system |
数据信息传输波形在使用信号带宽中选出46个跳频点,跳频速率为40000跳/秒,跳频点间隔15 MHz,46个跳频点在使用信号带宽中的相对频率如表1所示。
|
|
表 1 传输波形跳频频率相对位置 Tab.1 Transmit waveform hopping frequency relative position |
高可靠波形采用40000跳/秒的高速跳频技术实现抗干扰要求。其跳频图案由TOD信息,固定密钥和动态密钥3部分共同决定,且相邻跳频符号之间的频率间隔不低于50 MHz。其中,TOD信息由设备外部接入,各端机的固定密钥相同,因此接收端只需知道发射端的动态密钥即可跟踪上发射端的跳频图案。跳频方案如下:
1) 取消原跳频粗同步和报文头信息
设计跳频粗同步是为了降低首次入网时间,可以通过减少跳频同步的频点数来实现。如原方案中,使用信号带宽共有46个频点,新方案跳频频点只选择其中8个,且顺序固定。
2) 增加同步数量且动态密钥随同步一起传输
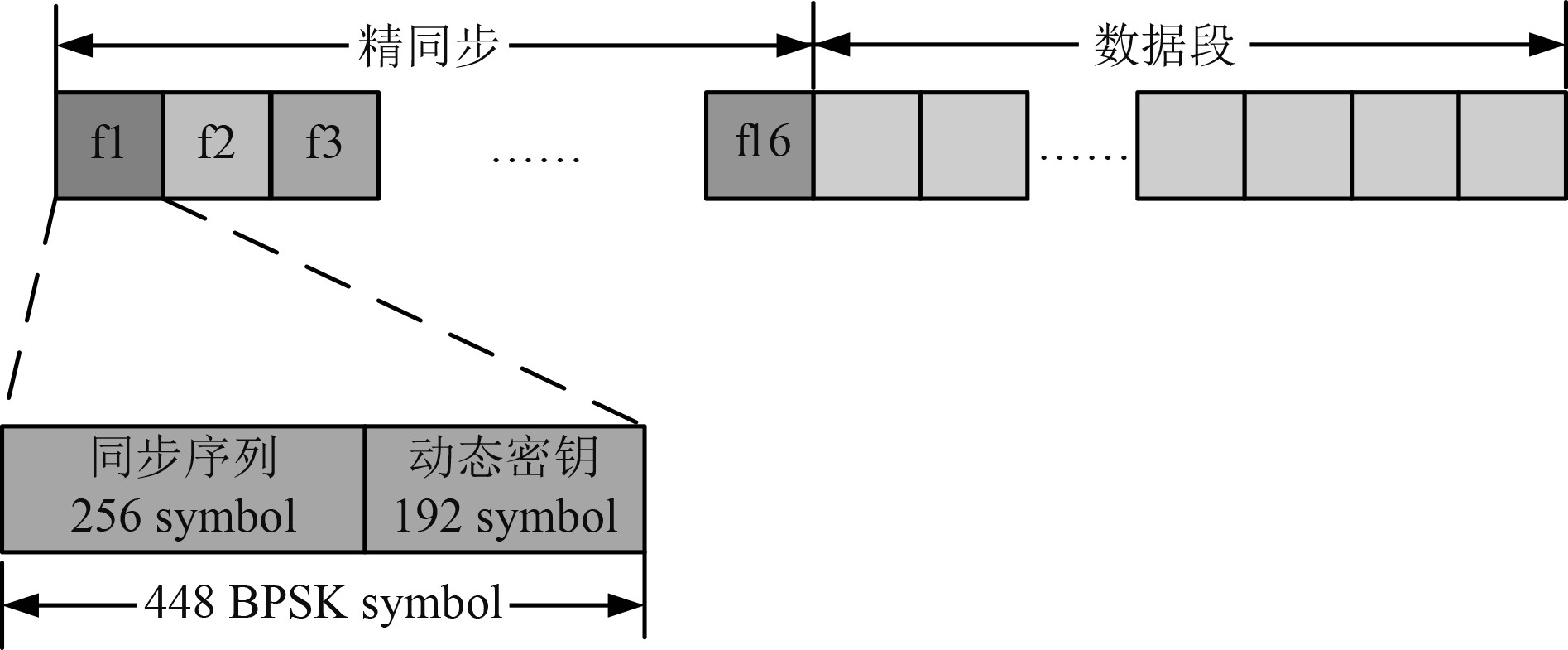
固定选择16个频点作为精同步的跳频频点,且这16个点位置相对固定。同步序列长256 bit,后面携带192 bit动态密钥信息。
|
图 3 帧格式 Fig. 3 Frame format |
3) 同步流程
接收端依旧采用慢跳方式,依次驻留在频点f1,f2,f3……,若同步后即可知道动态密钥。并由动态密钥与本地固定密钥和TOD信息共同生成跳频图案。动态密钥共32bit,添加16 bitCRC校验后组成48 bit,采用8进制RS(24,6)编码后,调制为192个BPSK符号。
高可靠数据波形跳频同步流程如下:
1)入网前慢扫描
在未入网的情况下,接收端依次在某个频率驻留8 ms时间,若同步未成功,则切换频点。考虑总跳频频点数为46个,则接收端一次频率驻留碰到跳频粗同步频率的概率为16/46,考虑75%概率被干扰,则成功碰到的概率为4/46,未碰到的概率为42/46。1 s时间可搜索125次,这125次未搜索到的同步频点概率为(42/46)^125=1.15e−5。
在已入网的情况下,每个同步头被干扰的概率为3/4,则16个同步头频点全部被干扰的概率为 (3/4)^16=1%,即同步成功概率为99%。
2)获取跳频图案后正常工作
若同步成功,则接收端可获取后续跳频图案信息,后续将跟随发射端跳频,完成数据接收工作。
3.3 跳频图案生成方案动态密钥共32 bit,分为2部分:高16位和低16位。均设计为2个16 bit计数器,即1,2,3,4…到2^16,然后重新循环到1。
动态密钥每4 ms更换一次,即由每个动态密钥可算出112个数据段的跳频图案。具体算法如下:
将动态密钥的2部分:高16位和低16位,分别利用m序列和rs序列生成LFSR序列。分别算出112个序列:x_m和x_rs。然后通过处理,得到跳频频点号Freq_num。
4 同步仿真仿真内容为在50%频率干扰下跳频同步的成功率,具体仿真流程如图4所示。

|
图 4 跳频同步仿真流程图 Fig. 4 Frequency hopping synchronous simulation flowchart |
发送端产生同步头序列并将每个同步头序列调制到固定的跳频频点上。接收端首先按顺序在已知的同步头频点上等待,每个频点上等待2帧的时间,在某一频点上同步成功后,根据同步头跳频图案在接下来的每一频点上进行同步运算。
由于同步头的数量共有16个,所以优先选择同步次数最多的点作为定时同步点。当不存在次数最多的同步点时,选择最大峰值对应的同步点作为定时同步点。
仿真结果如下:
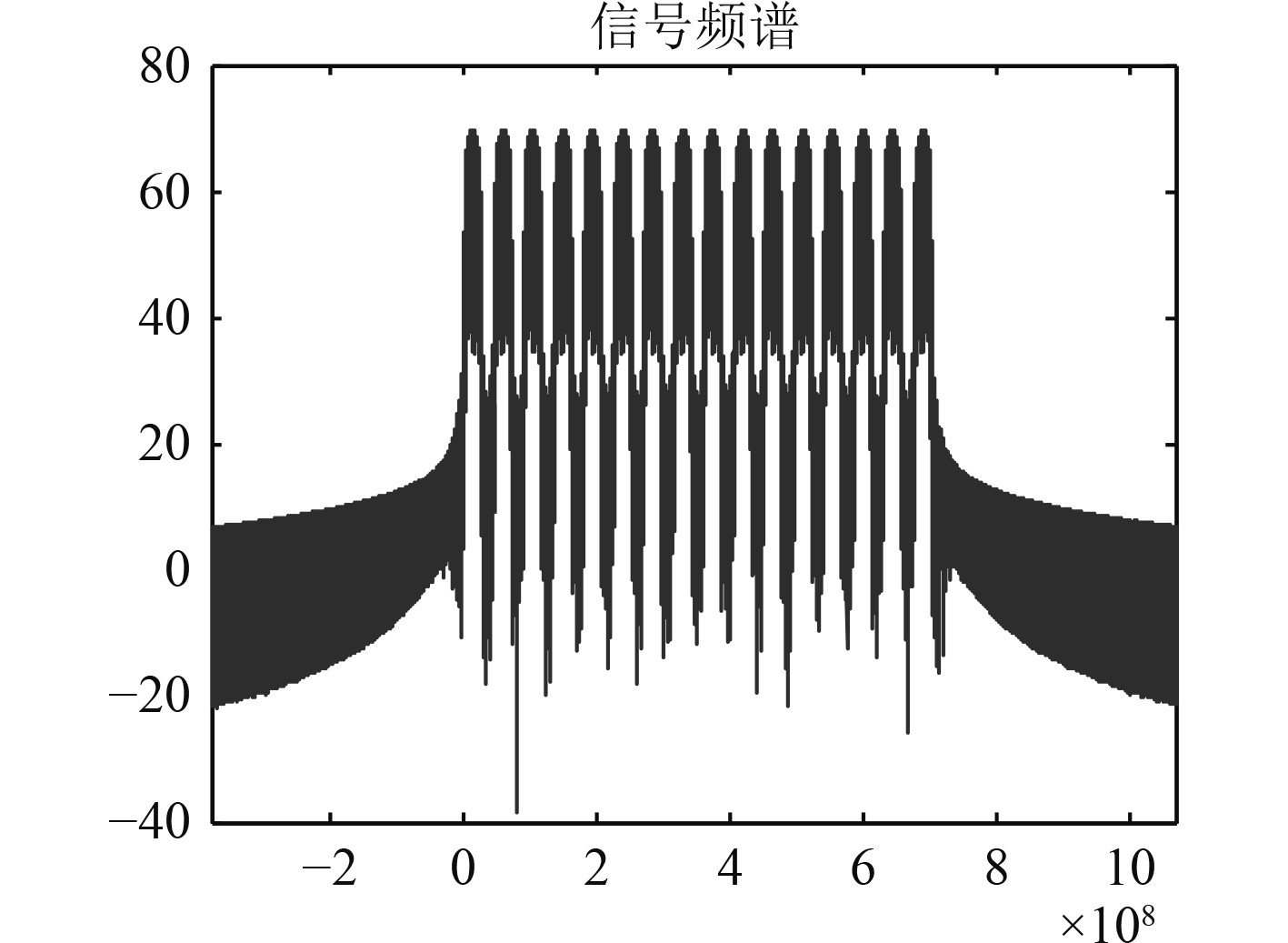
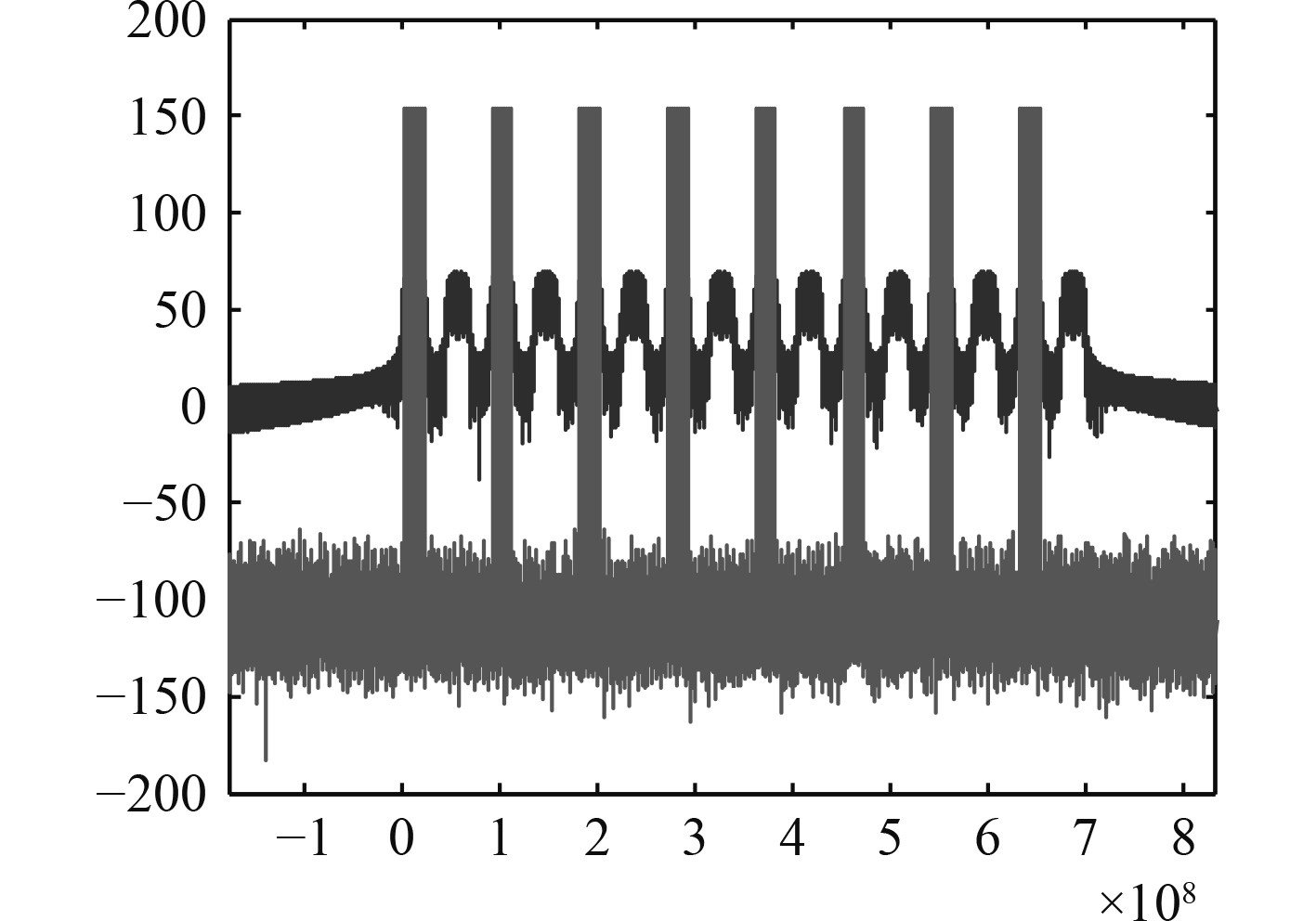
同步头频谱图如图5所示,同步头序列和频率干扰对比如图6所示。
|
图 5 同步头频谱图 Fig. 5 Synchronizing head spectrogram |
|
图 6 同步头序列和频率干扰频谱对比 Fig. 6 Comparison of sync head sequences and frequency interference spectrums |
m序列具有良好的周期相关性,只有当2个相同的m序列完全对齐时,相关值才会出现峰值。其他情况下相关值接近0,同步头序列的相关值如图7所示。

|
图 7 无干扰时的相关值 Fig. 7 Relevant value when there is no interference |
同步成功概率如图8所示。

|
图 8 跳频定时同步正确率曲线 Fig. 8 Frequency hopping timing synchronization accuracy curve |
仿真结果表明,忽略未搜索到同步频点的情况,在50%频率干扰下,当信噪比为−8 dB时,同步成功概率已经达到了0.99999。
5 结 语本文设计一种综合使用了精确时钟法、同步字头法、自同步法的跳频同步方法,克服现有跳频同步方法生成的跳频图案保密性不强问题,免除了对时钟精度和关网时间的限定要求。
高速信息同步包括了定时粗同步和定时精同步2个部分,定时粗同步采用的是计算相关峰的办法,精同步采用同步序列和动态密钥相结合,既简化了运算,又能够实现高精度的定时同步,为后续的技术应用奠定基础。仿真在50%频率干扰下,当信噪比为–8 dB时,同步成功概率已经达到了0.99999,证明了该同步方法能够实现快速可靠同步,满足高速数据传输要求,具备良好的应用价值。
| [1] |
TSU CP, CHANG DC. Modulation classification for mary CPM signals: based on PAM decomposition and phase detection methods[C]//Computer Communications and Networks (ICCCN), 2011 Proceedings of 20th International Conference on IEEE, 2021: 1–5.
|
| [2] |
WANG Y, LIU A, ZHANG Y, et al. Reduced-complexity superbaud timing recovery for PAM-based multi-h CPMreceivers[C]//Wireless Communications and Networking Conference(WCNC), 2013 IEEE, 2019: 3900–3904.
|
| [3] |
赵晋宇. 超短波跳频通信系统关键技术研究与FPGA实现 . 西安: 西安电子科技大学. 2012.
|
| [4] |
张洪铭, 闫实, 唐斌, 等. 海上无线通信技术: 现状与挑战[J]. 无线电通信技术, 2021, 47(4): 392-401. |
| [5] |
樊康敏. CPM收发机的关键技术研究[D]. 杭州: 浙江大学, 2018: 20–32.
|
| [6] |
李多烨. 连续相位信号的调制解调技术研究及其FPGA实现[D]. 成都: 电子科技大学, 2018.
|
| [7] |
潘晓丹. 深空通信中的调制技术分析与研究[D]. 西安: 西安电子科技大学, 2017.
|
| [8] |
刘晓明, 汪梦柔, 吴皓威, 等. SOQPSK信号的定时相位联合估计算法[J]. 江苏大学学报:自然科学版, 2019, 32(4): 443-448. |
| [9] |
乔慧. 连续相位调制信号载波同步研究[D]. 西安: 西安电子科技大学, 2018: 1−20
|
| [10] |
钟声. Multi-h CPM同步及序列检测技术研究[D]. 绵阳: 中国工程物理研究院, 2017: 1−52.
|
| [11] |
STARKIE T J S, SMITH L D. Ultrawideband antenna: US, US7327315[P]. 2018.
|
| [12] |
LALEZARI F. Ultra-broadband antenna system combining an asymmetrical dipole and a biconical dipole to form a monopole: US, US7339542[P]. 2018.
|
 2023, Vol. 45
2023, Vol. 45
