0 引　言

声呐是反馈海洋信息的最主要方式，由于水下环境复杂与声呐成像机制影响，声呐图像所受的噪声干扰远比光学图像更严重^[1]。斑点噪声是乘性噪声，因此导致图像质量严重下降，图像模糊，边缘细节丢失等，对后续的图像分割，图像识别等产生不利影响^[2]。因此研究声呐图像去噪算法具有重要意义。

近几年对于声呐图像去噪处理常使用的算法有：双树复小波变换、contourlet变换等，小波去噪并不能很好的得到边缘及轮廓特征^[3]。当前，光学图像去噪算法多种多样，如偏微分方程降噪^[4]、全变差去噪^[5]等。这些算法对去除高斯噪声效果明显，但对斑点噪声作用不是太理想。Goyal B等^[6]提到开合操作的协同实施已被证明在去除结构噪声方面非常有效。赵思雨等^[7]提到数学形态学比其他空域或频域图像处理方法具有一些明显的优势。数学形态学的去噪能力跟结构元素选择的好坏息息相关，如果选择不适合会导致图像出现模糊现象。Bregman迭代算法在求解某些类型的目标函数时收敛速度快，具能保持λ固定值作为去噪的优点。Liu X等^[8]提到分裂Bregman TV方法在保留边缘细节的同时，能有效重建图像，但在去噪过程中纹理和细节一起被去除。Wang X等^[9]提出的非下采样轮廓波变换(NSCT)不仅保留了轮廓波变换的特点，而且具有平移不变性，在许多图像处理过程中都具有重要意义。

针对以上问题，分裂Bregman TV模型有去噪。保边性，能够解决数学形态去噪导致图像整体模糊的缺点。通过数学形态学去噪，其拥有良好的去噪效果，能够解决分裂Bregman TV模型去噪效果不理想的缺点。受慕彩红^[10]、李智^[11]的启发，本文引入图像熵、梯度和边缘强度对Bregman TV的正则项系数进行改进，新的分裂Bregman全变差与数学形态学在非下采样轮廓变换（NSCT）的帮助下相结合，构建了一种新的图像融合去噪技术。该方法进一步保留了图像的边缘细节特征，改善了图像的均方差、峰值信噪比、信噪比和结构相似度。实验结果表明，该方法相较于使用基于小波变换和全变分的图像去噪^[11] 、传统的分裂Bregman TV、数学形态学，更能有效的去除噪声，PSNR、SNR、SSIM都得到了提高，MSE得到了改善。

1 分裂Bregman迭代去噪 1.1 引入熵、平均梯度、边缘强度

熵是由Clausius首先提出，用来评价能量在空间中的分布均匀程度，熵值越大说明能量分布越均匀^[12]。图像熵能够评价图像的平均信息量，随着噪声变化可以避免对图像梯度值的影响，从而更好地反映图像的变化^[13]。其表达式如下；

$ H=\sum_{i=0}^{R 55} p_{i} l g p_{i} ，$

(1)

式中， $ p_{i} $ 为图像灰度值为 $ i $ 的像素所占比例。通过熵的大小来衡量声呐图像信息量的多少。

Joseph^[14]在各向异性扩散滤波器中引入梯度对原始模型进行改进，得到了很好的效果。黄金等^[15]使用梯度对全变差的扩散系数进行改进，同样取得了良好的效果。图像平均梯度计算表达式如下；

$ G=\dfrac{1}{M \times N} \sum_{i=1}^{M} \sum_{j=1}^{N} \sqrt{\dfrac{\left(\dfrac{\partial f}{\partial x}\right)^{2}+\left(\dfrac{\partial f}{\partial y}\right)^{2}}{2}}。$

(2)

式中： $ M \times N $ 为图像大小； $ \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y} $ 分别为水平梯度和垂直梯度。平均梯度反映图像的清晰度和纹理的变化。

图像中的细节信息通过边缘强度反映，其值越大，图像的纹理越清晰，视觉效果更好^[16]。其定义式如下；

$\begin{aligned}[b] E(x, y)=&|(f(x-1, y-1)+2 f(x-1, y))-\\ & (f(x+1, y-1)+2 f(x+1, y)+f(x+1, y+1))|+ \\ & |(f(x-1, y-1)+2 f(x, y-1)+f(x+1, y-1))-\\ & (f(x-1, y+1)+2 f(x, y+1)+f(x+1, w+1))|。\end{aligned}$

(3)

式中： $ f(x, y) \text { 和 } E(x, y) $ 分别为图像在 $ (x, y) $ 的系数和边缘强度。利用图像熵、平均梯度、边缘强度对各向异性TV的正则项系数进行改进。

1.2 各向异性TV模型

各向异性模型^[17]：

$ \arg \min \left\|\nabla_{x} u\right\|_{1}+\left\|\nabla_{v} u\right\|_{1}+\frac{\mu}{2}\left\|u-u_{\theta}\right\|_{9}^{g} ，$

(4)

设 $ d_{x}、d_{y} $ 代替 $ \nabla_{w} u、\nabla_{y} u $ ，将上式变换为一个限制性问题，即

$ \arg \min \left\|d_{x}\right\|_{1}+\left\|d_{y}\right\|_{1}+\frac{\mu}{2}\left\|u-u_{o}\right\|_{2}^{z} 。$

(5)

为了平衡正则项和保真项之间的权重需要加入拉格朗日乘子，目的是在其去噪过程中有很好的保边能力。当参数 $ \lambda $ 较小时，正则项系数变大，去除图像噪声信息，保留图像边缘特征。引入图像熵、平均梯度、边缘强度对传统正则参数进行改进， $ \lambda $ 为：

$ \lambda=e^{-\left(\frac{H(x, y) \times G(x, y)}{E(x, y)}\right)} 。$

(6)

式中： $ H(x, y) 、G(x, y)、E(x, y) $ 分别为图像熵；平均梯度、边缘强度通过式（1）、式（3）计算可得。在式（5）中加入新的正则参数 $ \lambda $ 可得：

$\begin{aligned}[b] {\rm{arg}}\;{\rm{min}} ||d_x|| _1+&||d_y||_1+\frac{\mu}{ 2}||u-u_0||^2_2+\\ & e^{-\left(\frac{H(x,y)*G(x,y)}{E(x,y)}\right)}||d_x-\nabla_xu-b^k_x||^2_2+\\ & e^{-\left(\frac{H(x,y)*G(x,y)}{E(x,y)}\right)}||d_y-\nabla_yu-b^k_y||^2_2。\end{aligned}$

(7)

式中， $ b^{k}=\left(b_{x}^{k}, b_{y}^{k}\right)^{\rm T} $ 为辅助向量， $ b^{k} $ 的迭代式为^[18]

$ b^{k+1}=b^{k}+\nabla u^{k+1}-d^{k+1}。$

(8)

式中， $ d^{k}=\left(d_{x}^{k}, d_{y}^{k}\right)^{\rm T} $ 。需求出 $u $ ，解决下列子问题^[19]：

$\begin{aligned}[b] & \partial_u\left(\dfrac{\mu}{2}||u-u_0||^2_2+\frac{\lambda}{2}||d^k_x-\nabla_xu-b^k_x||^2_2+\frac{\lambda}{2}||d^k_y-\nabla_yu-b^k_y||^2_2 \right)=\\ & 0 \Leftrightarrow \mu\left(u - u_{i}\right) - \lambda \nabla_{m}^{\rm T}\left(d_{m}^{k} - \nabla_{x} u - b_{x}^{k}\right) - \lambda \nabla_{\mathrm{v}}^{\rm T}\left(d_{\Downarrow}^{k} - \nabla_{\nabla} \mathrm{w} - b_{m}^{k}\right) =\\ &\theta \Leftrightarrow(\mu I-\lambda \triangle) u=\mu u_{\theta}-\lambda d \hat{v}\left(d^{\lambda}-\sigma^{\Delta}\right) ，\\[-14pt] {}\end{aligned} $

(9)

利用广义收缩公式，将 $ d_{x} \text { 和 } d_{y} $ 更新为；

$ d_{x}^{k+1}=\operatorname{shrink}\left(\nabla_{x} u^{k+1}+b_{x}^{k}, \frac{1}{\lambda}\right) ，$

(10)

$ d_{y}^{k+1}=\operatorname{shrink}\left(\nabla_{y} u_{y}^{k+1}+b_{y}^{k}, \frac{1}{\lambda}\right)。$

(11)

该算法流程如下：

步骤1　参数初始化。

$ u^{0}=u_{o}, d_{ \pm}^{0}=d_{w}^{d}=b_{ \pm}^{\theta}=b_{v}^{0}=0 $ ，gamma=0.1，lamda= $e^{-\left(\frac{H(x, y) \times G(x, y)}{B(x, y)}\right)} $ 。 $ {lamda} $ ， $ { gamma } $ 为正则化参数。

步骤2　开始迭代。

利用式（10）和式（11）求出 $d_{x}^{k+1}和 d_{\psi}^{k+1}$ ，利用式（8）求出 $b_{*}^{k+1}和b_{v}^{k+1}$ 。

步骤3　循环停止。

判断 $ \dfrac{\left\|u^{k}-u^{k-1}\right\|_{2}}{\left\|u^{k}\right\|_{2}}< { tol } $ 是否成立， $ { tol } $ 表示停止条件。若成立循环停止，输出结果，若不成立返回步骤2继续执行循环，直到判断成立。

2 数学形态学

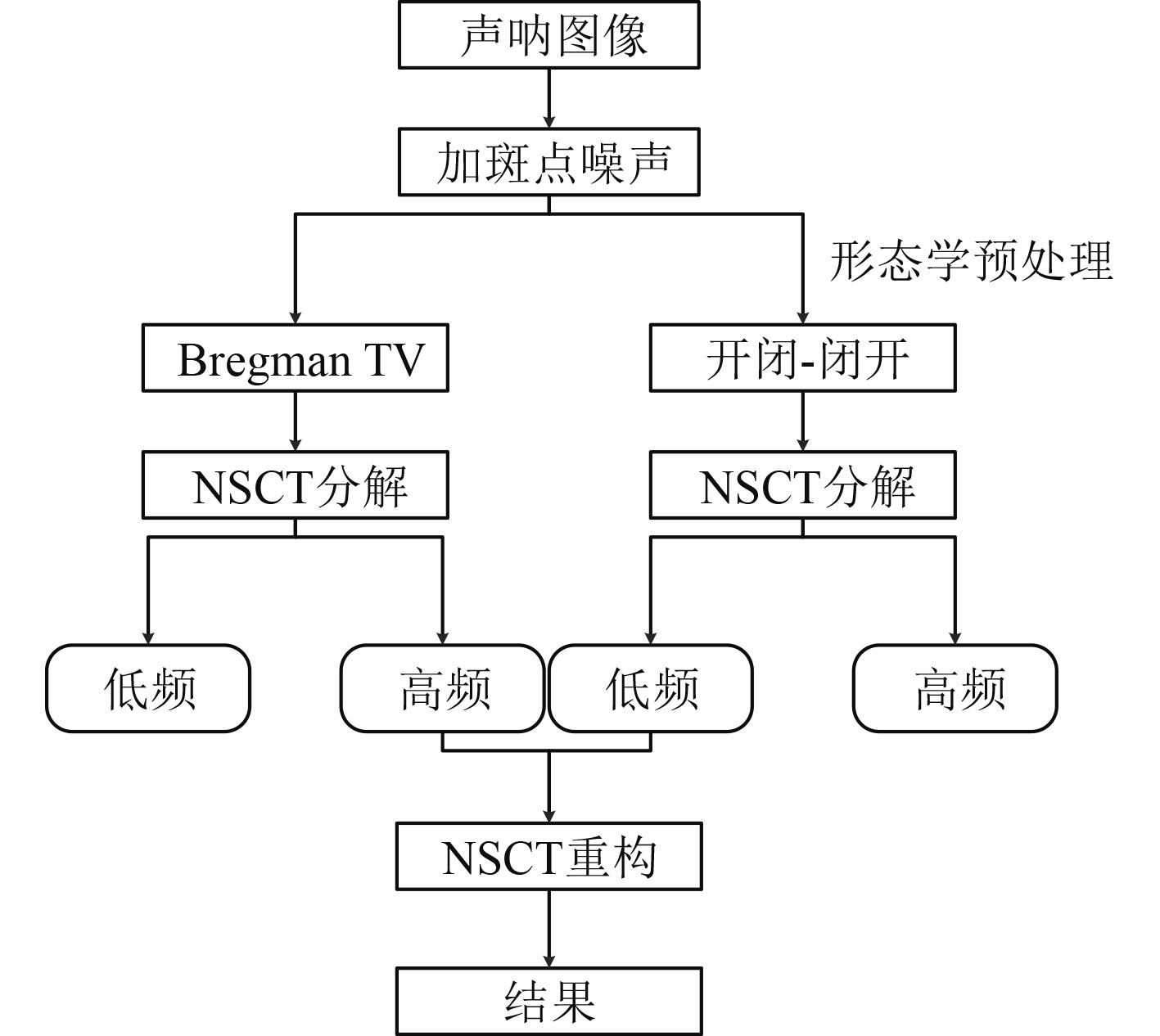
数学形态学由一组形态学的代数运算子组成，其基本运算有4个：膨胀、腐蚀、开启和闭合^[20]。该方法的原理是使用结构元素来收集图像的信息，需要结构元素在图像中不断滑动时，了解图像的结构特征。本文将其应用在声呐灰度图像中，利用多结构元素对图像进行开启-闭合和闭合-开启运算，达到去除噪声点的目的。

设 $ f(x, y) $ 代表图像， $ B(x, y) $ 代表结构元素， $ C(x, y) $ 代表另一种结构元素。开运算是利用结构元素 $ B $ 对灰度图像先进行腐蚀再进行膨胀，即

$ f^{\circ} B=(f \ominus B) \oplus B 。$

(12)

其中： $ f \ominus B $ 为腐蚀运算； $ f \oplus B $ 为膨胀运算。

闭运算是用结构元素 $ C $ 对灰度图像先进行膨胀再进行腐蚀，即

$ f \cdot B=(f \oplus B) \ominus C 。$

(13)

开运算的作用是删除比较细小的物体，除去边缘其他不必要的内容，而闭运算的作用是填充物体内细小的空洞^[21]。

开启-闭合是利用结构元素 $ B $ 对图像进行开运算，然后用结构元素 $ C $ 进行闭运算。闭合-开启利用结构元素 $ B $ 对图像进行闭运算，再用结构元素 $ C $ 进行开运算。

3 NSCT

非下采样轮廓波变换（Non-Subsampled Contourlet Transform，NSCT）能够很好捕捉图像细节，具有Contourlet变换的特点, 同时还拥有平移不变特性^[22]。NSCT分别使用非下采样金字塔和方向滤波器对图像进行多尺度分解和各尺度子带图像进行方向分解，从而获得不同尺度、不同方向的子带图像^[10]。其分解过程如图1所示。

4 本文方法的算法流程

步骤1　输入声呐灰度图像。

步骤2　对其添加斑点噪声。

步骤3　对步骤2进行Bregman TV去噪。

步骤4　对步骤2进行数学形态学去噪。

①选取合适的2个结构元素。

②利用结构元素1对灰度图像开运算，再利用结构元素2进行闭运算。

③利用结构元素1对灰度图像闭运算，再利用结构元素2进行开运算。

④将②③两个步骤生成的图像进行加权融合。

步骤5　对步骤3和步骤4的结果利用NSCT分解。

步骤6　将Bregman TV的高频与数学形态学的低频进行NSCT重构。

步骤7　输出图像。

实验步骤如图2所示。

5 实验结果

为验证本文方法去噪的效果，选择3张 $ 256 \times 256 $ 声呐图像（见图3），对其添加方差为0.3的斑点噪声（见图4），运用本文方法对其进行处理，得到的图像与数学形态去噪、分裂Bregman TV去噪、基于小波变换和全变分的图像去噪^[11]进行视觉效果对比如图5和图7所示。

从图5～图7可知，在斑点噪声为0.3时，数学形态学去噪效果明显，但同时图像部分出现模糊。各向异性TV去噪后，在保留边缘信息方面效果好，有一定的降噪能力，但去噪效果并不是很理想。基于小波变换的TV去噪后，边缘细节丢失，图像整体出现模糊，降噪能力低，在图6（c）尤为明显。而本文方法结合了数学形态学与TV去噪的优点，图像中噪声点明显减少，边缘细节丰富。从视觉效果上看，本文方法比前3种方法去噪效果更好。

为了进一步客观地评估本文方法，添加方差0.2，0.3，0.4，重复进行多次实验，采用峰值信噪比(Peak Signal to Noise Ratio，PSNR)、信噪比（Signal-Noise Ratio，SNR）、结构相似度（Structural Similarity Index Measure，SSIM）和均方误差（Mean Squared Error，MSE）作为质量评价指标，如表1所示。

从表1～表3数据显示，通过本文方法去噪后的PSNR、SNR和SSIM均比各向异性TV去噪、数学形态学去噪、基于小波变换的TV去噪高，MSE均比前3种方法低。随着噪声的增加，在使用图4（a）时，本文方法比前3种方法PSNR均高1 dB左右，SNR均高1dB左右，SSIM均高0.05左右。在使用图4（b）时，本文方法比前3种方法PSNR均高0.7 dB左右，SNR均高0.7 dB左右，SSIM均高0.02左右。在使用图4（c）时，本文方法比前3种方法PSNR均高1 dB左右，SNR均高1 dB左右，SSIM均高0.09左右。综上，数学形态学的各项指标均比传统的各向异性TV和基于小波变换的TV去噪高，说明数学形态学去噪能力优于前2种方法。而本文方法各项指标变换稳定，优于其他3种方法。随着噪声的增加，本文方法去噪效果更好，同时保留了更多的边缘，且图像没有发生模糊现象。

6 结　语

传统去噪方法在去除声呐图像斑点噪声的同时，难以拥有很好的细节信息。提出一种基于改进Bregman TV与数学形态学的NSCT声呐图像融合去噪技术，弥补了使用数学形态学导致模糊图像的缺点和使用分裂Bregman TV去噪后导致图像细节信息丢失的缺点。通过仿真实验表明，本文方法比数学形态学去噪、传统的分裂Bregman TV去噪、基于小波变换和全变分的图像去噪更能够有效的去除斑点噪声，PSNR、SNR、SSIM和MSE都得到了不同程度的改善。本文方法的缺点是需要根据图像的结构特征选取对应的数学形态学所需的结构元素，没有固定的某种结构元素。