为了实现碳达峰、碳中和目标,减小能源消耗和环境污染,大多数沿海国家纷纷把目光投向海洋可再生能源的开发利用。波浪能以分布范围广,能量密度大和清洁污染小等优点,在海洋可再生能源中得到了广泛关注与研究[1]。目前国内外设计研发的波浪能装置种类众多,以英国Pelamis为代表的筏式波浪能转换装置,由于结构简单,生存能力强,转换效率高等特点,在离岸式波浪发电装置中是比较不错的选择,近几年对筏式波浪能转换装置展开的研究逐渐增多。张永良等[2]从理论角度分析了双浮体式波能转换装置的水动力性能,通过分离变量、特征函数展开法逐步确定函数的表达式和势能的待定参数,通过假设装置是理想线性粘性阻尼,从而得出装置运动响应和透射系数、反射系数及转换效率。Arena 等[3]对波浪下起伏运动的二维对称浮体装置展开研究,发现装置理论上的最大能量转换效率仅为 50%,并且能量转换的有效频率范围较窄。Ning等[4]以比较新颖的方式评估由摆式波浪能装置和防波堤组合系统的性能,研究了波浪周期和波高、尺寸和激励电流等各种参数对装置水动力性能的影响,在适当的阻尼条件下,可以观察到系统的转换效率可达约24%,而透射系数保持在50%以下的范围。Zhao等[5]在此基础上进一步研究,结果表明,与单浮体相比,防波堤型波浪能发电装置在不影响海岸保护性能的情况下有效提高了转换效率中在装置的背风侧适当布置固定浮体式结构,可以实现二维对称装置转换效率大于50%。Chen等[6]推导了链接的双浮体耦合运动方程,并在自定义函数里编译实现,对装置进行了数值模拟和物理实验分析,得到了不同浮体参数对装置转换效率的影响。综上所述,目前基于Navier-Stokes方程的重叠网格技术对流体与铰接筏体之间全耦合方面的研究还需进一步深入,本文基于粘性CFD理论,考虑筏体之间的连接及系泊的影响,建立6种不同参数的筏式波浪能装置筏体和系泊耦合模型。通过改变模型的比例与长度结合展开比较分析,选取其中一种发电效率较高的模型,分析波频、波高对装置转换效率和透射系数的影响,并综合考虑装置的对称性、成本以及效率的最优化方案,为在不同海况下的筏式波浪能发电装置设计提供参考。
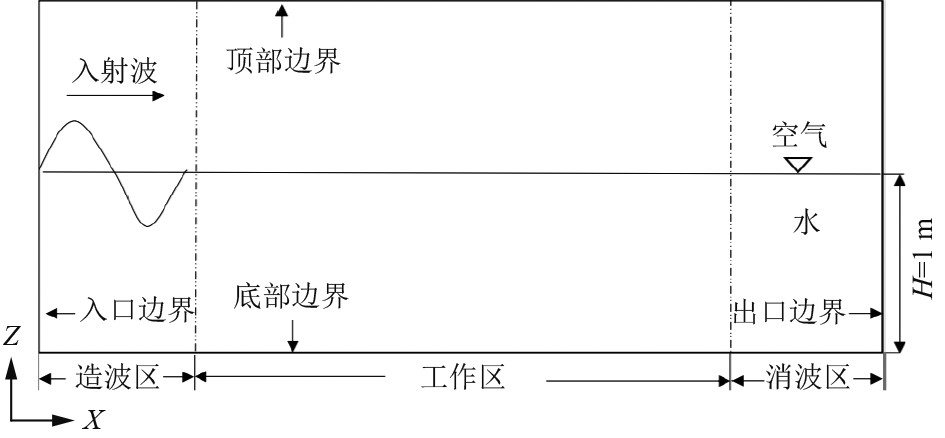
1 数值波浪水槽 1.1 波浪数值水槽模型计算域的大小直接影响着数值模拟计算的结果,因此选取一个合适的计算域十分关键。根据文献设置的计算域[7],如图1所示。水槽沿波浪传播方向为x轴;波高方向为z轴;与水槽垂直的方向为y轴。在x方向的计算域长度选取为6L(L为波长),水深h为1 m,造波采用的是Stokes五阶VOF波模型,其中入射波高H为0.2 m,波周期T为1.37 s,粘性状态模型选用层流模型。所用模型的边界条件设置:入口边界条件和出口边界条件设置为速度入口;顶部边界设置为压力出口;底部边界条件设置为壁面;前后2个沿x轴方向的面设置为对称平面。为了使软件准确模拟二维的模型,在y方向设置一层网格的宽度,水槽前后两端各设置1.5倍波长的力消波,与之前实验中采取的阻尼消波相比,采用力消波的方法能更好消除水槽壁面产生的反射波对入射波浪的影响,为筏式装置提供一个稳定的波浪环境。
|
图 1 数值波浪水槽的示意图 Fig. 1 Schematic diagram of numerical wave tank |
网格和时间步长决定着数值计算的精度,在用CFD软件对模型进行网格划分时,生成网格的方式为自动网格,选用切割体网格单元生成器网格来进行网格划分。由于流体变化复杂,需要较为精细的网格捕捉流场的变化情况,因此本文围绕波浪情况设置了加密区和过渡区,且离自由液面越近,网格越密。为了确定使计算结果收敛的最合理时间步长和网格尺寸,设置了4个模型,其时间步长和网格尺寸如表1所示。
|
|
表 1 模型时间步长与网格尺寸设置 Tab.1 Model time step and mesh size settings |
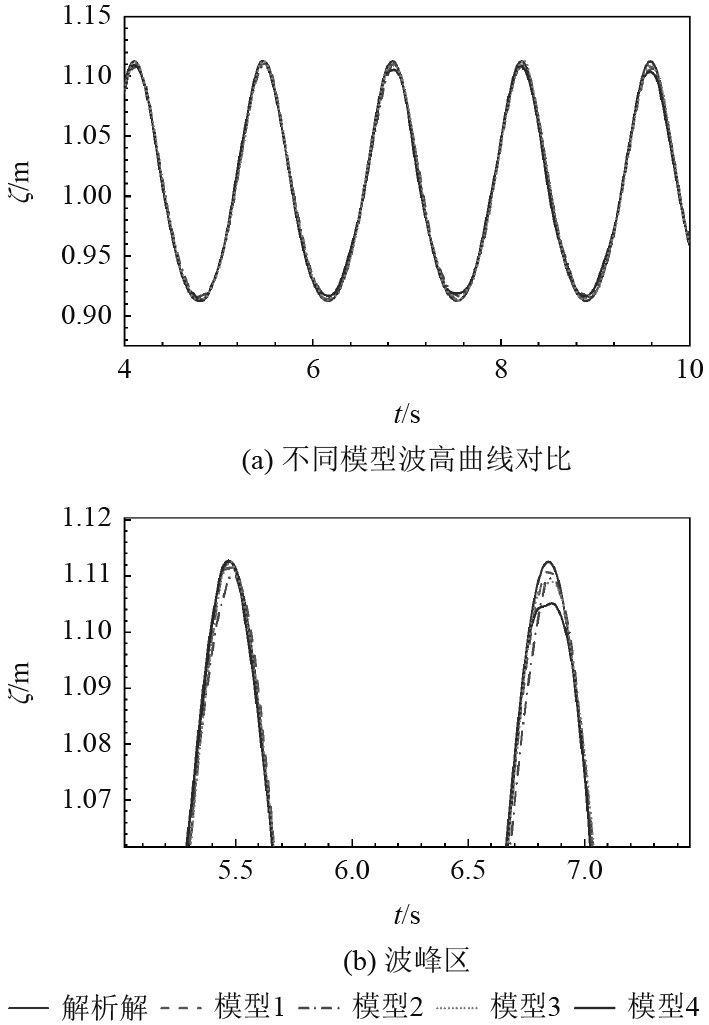
图2为不同模型在4~10 s时间内的波高曲线。通过对比图中数据可得,模型1、模型3、模型4在时间步长相同的情况下,改变液面的网格大小,模型1和模型3的波高与周期方面基本吻合,而网格较稀疏的模型4在波峰区与波谷区存在差别,可以判断模型1和模型3的网格满足收敛性要求。考虑计算精度与计算成本,模型1的网格较模型3的网格更为合适。
|
图 2 网格尺寸和时间步长收敛性分析 Fig. 2 Mesh size and time step convergence analysis |
通过对比模型1和模型2发现,在波高和周期上,不同的时间步长,波浪数值结构非常接近,因此为节约计算成本和时间,选择时间步长为T/1000。
最后综合考虑计算精度与计算成本,选择网格1为最终的计算网格。
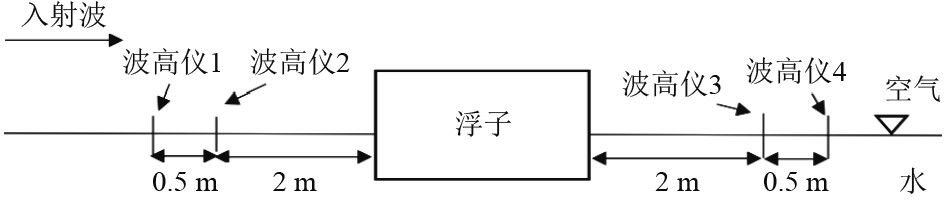
2 波浪与物体相互作用模型验证为了验证在波浪作用下浮子运动的准确性,参考Ning的物理实验模型,在整个CFD方法模拟过程中,静水深度h固定为1 m,吃水d=0.2 m,入射波高H=0.2 m,测试波周期从 1.16~2.42 s,相应的无量纲相对宽度 B/L(宽度 B与波长 L 之比)从 0.28 变化到 0. 12。将波高仪1和波高仪2放置在浮子前用于分离入射波高Hi 和反射波高Hr,造波板与波高仪1间距47.5 m,波高仪1和波高仪2的间距为0.5 m,波高仪2与浮子间距2 m,另外2个波高仪在浮子另一侧对称布置,用于分离透射波高 Ht,如图3所示。
|
图 3 波高仪布置的示意图 Fig. 3 Schematic diagram of wave height meter arrangement |
用两点法[8]分离Hi,Hr和Ht。两点法通常是指,2个相邻的波高仪在入射波行进方向上同步监测波浪,利用Fourier级数分析方法进行分离,可计算出入射波中各种波频间隔成分波的幅值以及透射系数。
基于线性波理论合成波中入射、反射成分波的波浪时间序列为:
| $ \left\{ \begin{gathered} {\eta _i} = {a_i}\cos \left( {kx - \omega t + {\varepsilon _i}} \right) ,\\ {\eta _r} = {a_r}\cos \left( {kx + \omega t + {\varepsilon _r}} \right)。\\ \end{gathered} \right. $ | (1) |
式中:
| $ \left\{ \begin{gathered} {A_1}\cos \omega t + {B_1}\sin \omega t = {\left( {{\eta _i} + {\eta _r}} \right)_{x = {x_1}}} = {\eta _1},\\ {A_2}\cos \omega t + {B_2}\sin \omega t = {\left( {{\eta _i} + {\eta _r}} \right)_{x = {x_2}}} = {\eta _2}。\\ \end{gathered} \right. $ | (2) |
| $ \left\{ \begin{gathered} {A_1} = {a_i}\cos \left( {k{x_1} + {\varepsilon _i}} \right) + {a_r}\cos \left( {k{x_1} + {\varepsilon _r}} \right) ,\\ {B_1} = {a_i}\sin \left( {k{x_1} + {\varepsilon _i}} \right) - {a_r}\sin \left( {k{x_1} + {\varepsilon _r}} \right),\\ {A_2} = {a_i}\cos \left( {k\Delta x + k{x_1} + {\varepsilon _i}} \right) + {a_r}\cos \left( {k\Delta x + k{x_1} + {\varepsilon _r}} \right)。\\ {B_2} = {a_i}\sin \left( {k\Delta x + k{x_1} + {\varepsilon _i}} \right) - {a_r}\sin \left( {k\Delta x + k{x_1} + {\varepsilon _r}} \right) 。\\ \end{gathered} \right. $ | (3) |
| $ \left\{ \begin{gathered} {K_{ave}} = \frac{{{a_r}}}{{{a_i}}},\\ \\ {H_i} = \frac{{{H_s}}}{{\sqrt {1 + {K_{ave}}^2} }},\\ \\ {H_r} = \frac{{{H_s}}}{{\sqrt {1 + {K_{ave}}^2} }}{K_{ave}}。\\ \end{gathered} \right. $ | (4) |
其中:A1,A2,B1,B2为Fourier系数;
|
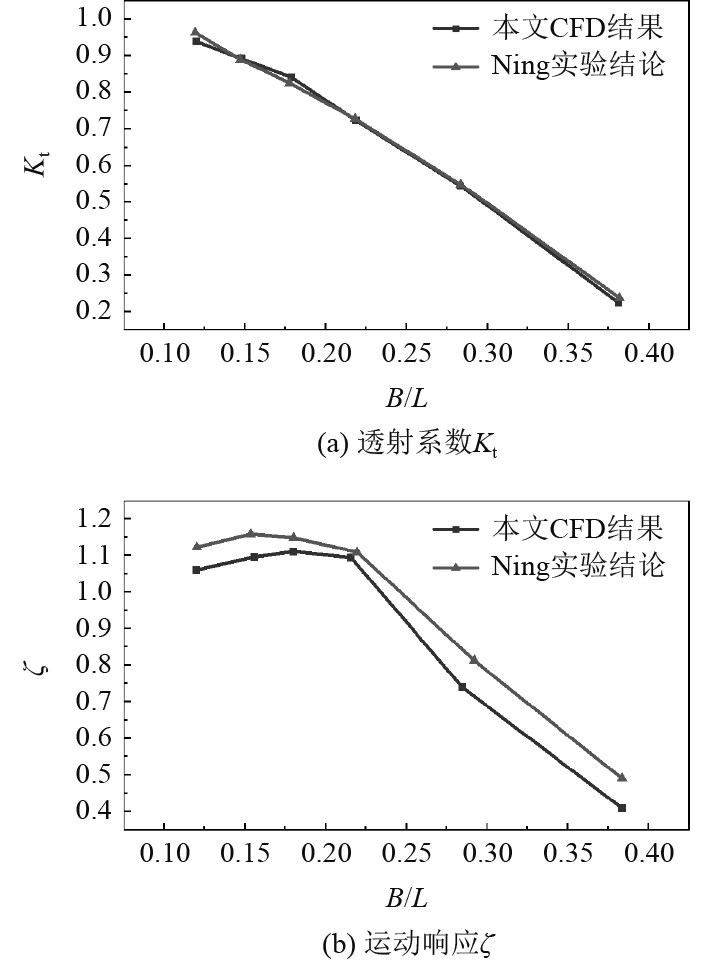
图 4 不同数值模型计算结果与Ning等的实验结果对比图 Fig. 4 Comparison between the calculation results of different numerical models and the experimental results of Ning et al. |
可以看出,随着相对宽度(B/L)增大,运动响应系数上升,在0.15~0.20之间达到最大,然后逐步下降,而透射系数则是一直处于下降趋势,这说明相对宽度对物体在波浪能中的运动状态和捕获能量方面有一定影响。另外,本文所采用的层流模型CFD数值模型求得的透射系数Kt和运动相应ζ与Ning[4]等论文中的实验结果吻合较好,验证了波与物体作用模型的准确性。
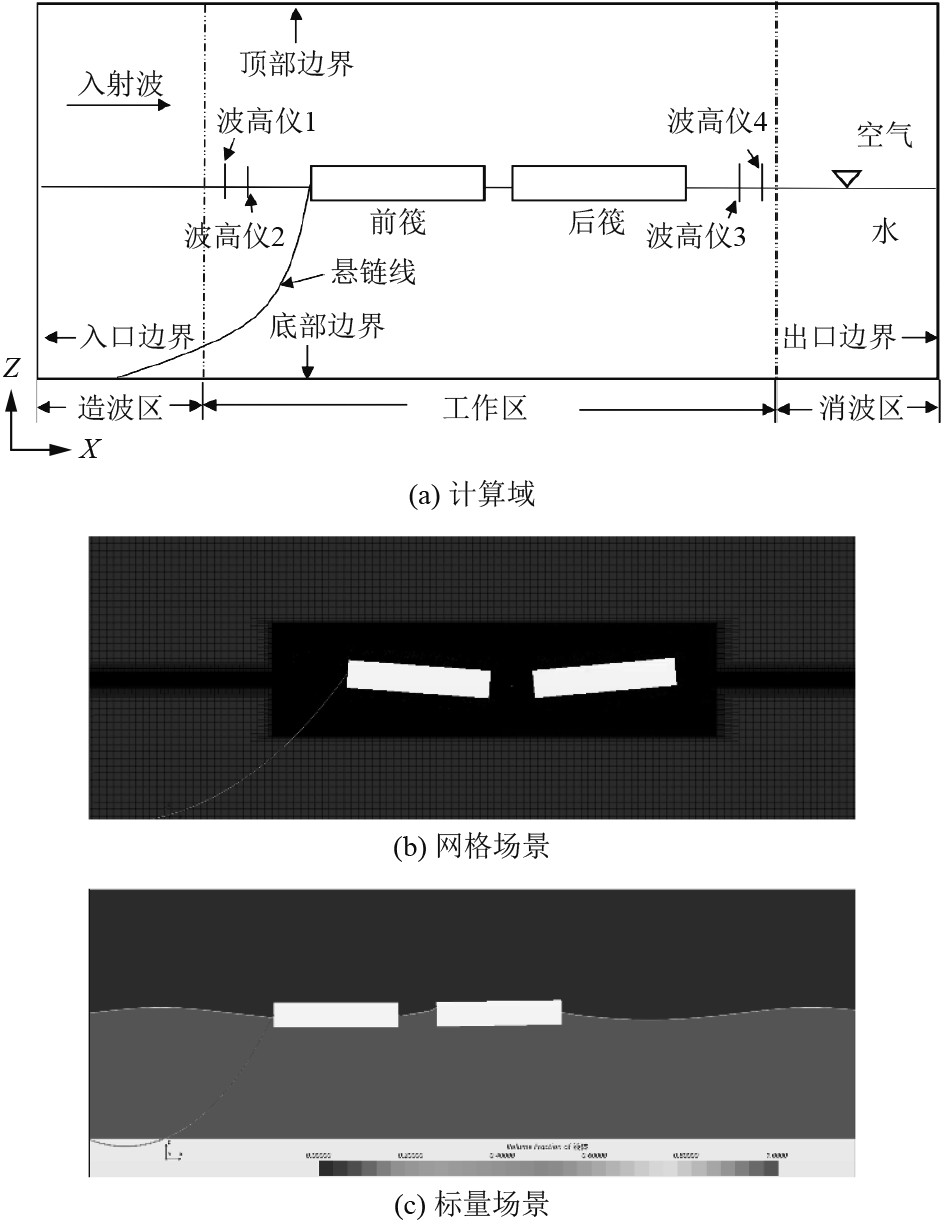
3 数值计算与结果分析 3.1 模型设置在已进行验证过的数值水槽中对两节筏式波浪能发电装置研究,选取6组不同尺寸的筏式装置进行数值模拟,参数设置如表2所示。筏的高度均为0.2 m,浸没深度为高度的一半,入射波高为0.1 m,前筏端部用一根悬链线作为系泊设备,松弛状态下长度为2 m,刚度为10000 N/m。运用CFD软件中的重叠网格和6自由度体运动功能模拟物体运动,在筏式装置的网格设置中将沿x方向的尺寸调成自由液面尺寸的一半,其他方向与自由液面尺寸相同。这主要是为了避免产生窄隙共振现象[9],导致装置中间的波高增加,影响对装置实际转换效率的监测。其中,前筏长度为1 m,后筏长度为1 m的B模型计算域、网格以及标量场景,如图5所示。
|
|
表 2 模型参数 Tab.2 Model parameters |
|
图 5 模型B的数值模拟过程 Fig. 5 Numerical simulation process of model B |
为了反映客观规律,方便对数据结果进行讨论,首先对波频
| $ \overline \omega = \frac{H}{{\sqrt {g{D_r}} }}\omega 。$ | (5) |
式中:
| $ {P_{in}} = \frac{1}{8}\rho {\text{g}}{H^2}B\frac{\omega }{{2k}}\left( {1 + \frac{{2kh}}{{\sin h\left( {2kh} \right)}}} \right) 。$ | (6) |
式中:
| $ {P_{ave}} = \frac{1}{T}\mathop \int \nolimits_{{t_1}}^{{t_1} + T} \frac{1}{2}{b_{pto}}I{v^2}{\text{d}}t 。$ | (7) |
式中:t1时刻物体运动达到稳定的时间。
| $ \eta {\text{ = }}{P_{ave}}/{P_{in}} \times 100\text% 。$ | (8) |
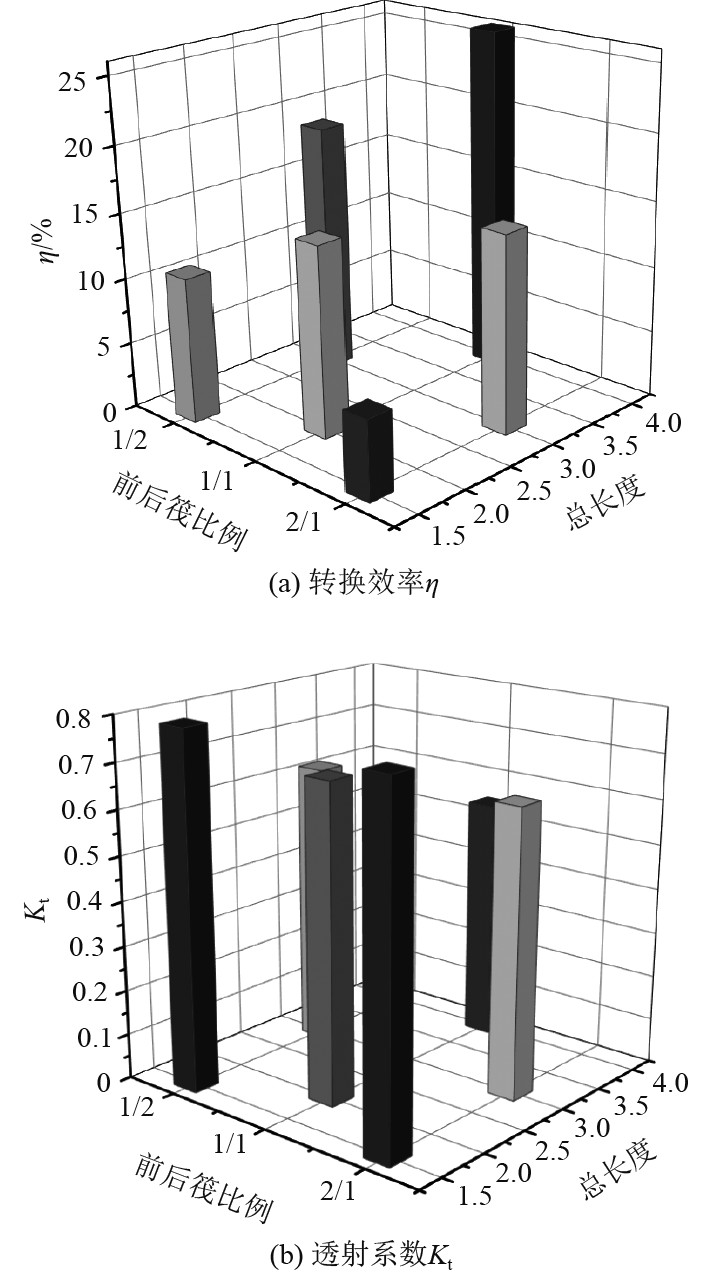
在其他波浪环境参数不变的情况下,通过改变几何尺寸和比例,依次从A到F模型进行数值模拟,对装置的转换效率
|
图 6 几何比例尺寸对装置水动力性能的影响 Fig. 6 Influence of geometric proportions on the hydrodynamic performance of the device |
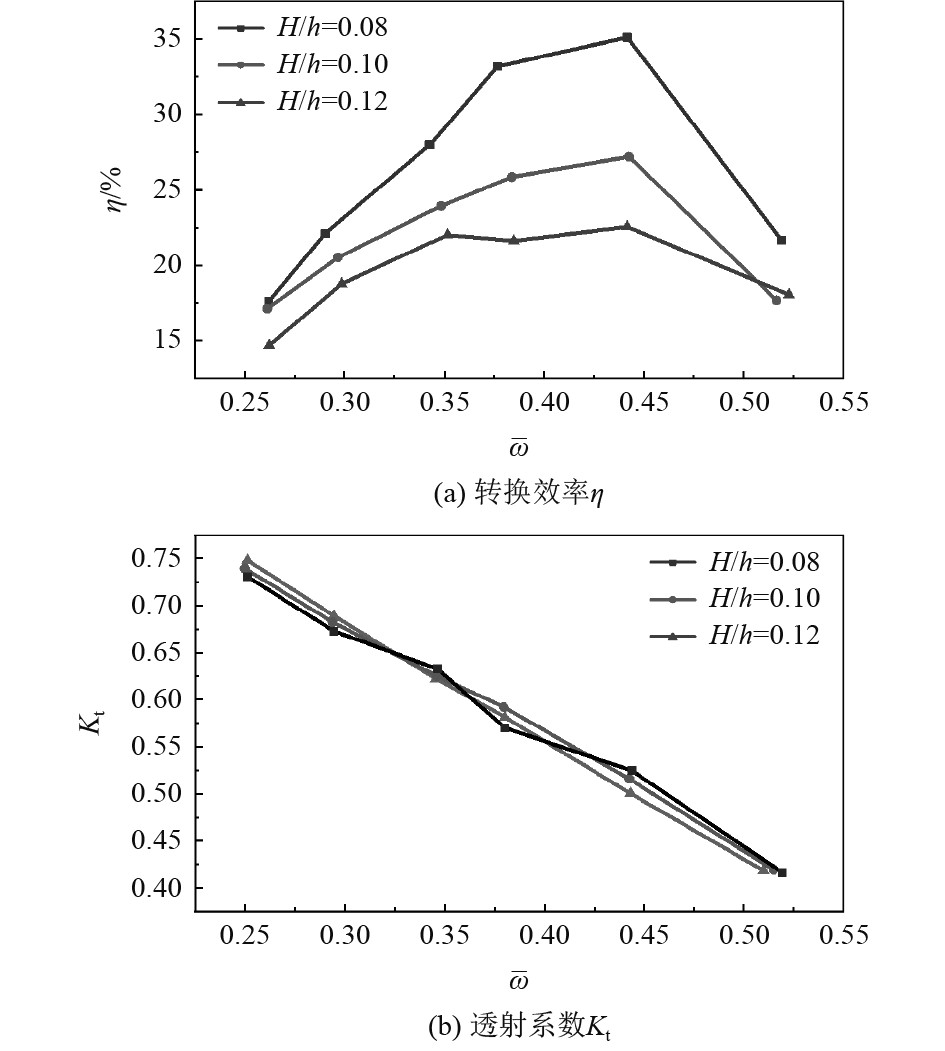
在研究了6种不同几何尺寸对装置转换效率
|
图 7
不同波高下
|
基于CFD方法研究了两节筏式波浪能发电装置的几何尺寸、波频、相对波高H/h、装置转换效率
1)筏式装置总长度相同时,前筏较短,后筏较长的装置具备更好的转换效率,几乎是相反比例装置转换效率的2倍;筏式装置比例相同时,随着总长度的增加,转换效率提高,但装置的制造成本也是必须考虑的问题,所以可尽量将筏式装置设计为对称的形状,在未来生产和投入使用上更具有发展前景。
2)在一定范围内的相对波高H/h与筏式装置的转换效率呈反比例关系,即相对波高越小,转换效率越好;当相对波高不变时,装置转换效率随着波频先增大后减小,装置发生共振时转换效率最大,并且物体的几何尺寸决定着共振频率,一旦波频太大后,转换效率反而减小。
3)装置前后筏比例、相对波高H/h等因素对透射系数Kt影响较小,Kt随着装置总长度与波频的增大而减小。
| [1] |
崔琳, 李蒙, 白旭. 海洋可再生能源技术现状与发展趋势[J]. 船舶工程, 2021, 43(10): 22-33. CUI Lin, LI Meng, BAI Xu. Current situation and development trend of marine renewable energy technology[J]. Ship engineering, 2021, 43(10): 22-33. |
| [2] |
ZHENG, S. M, ZHANG, Y. L. Wave diffraction and radiation by multiple rectangular floaters[J]. Journal of Hydraulic Research, 2016, 54(1): 102-115. DOI:10.1080/00221686.2015.1090492 |
| [3] |
ARENA F, ROMOLO A, MALARA G, ASCANELLI A. On design and building of a U-OWC wave energy converter in the Mediterranean Sea: A case study. [C]// Paper presented at the ASME 2013International Conference on Ocean, Offshore and Arctic Engineering , 2013.
|
| [4] |
NING D Z, ZHAO X L. Hydrodynamic performance of a pile-restrained WEC-type floating breakwater: An experimental study[J]. Renewable Energy, 2016, 95: 531-541. DOI:10.1016/j.renene.2016.04.057 |
| [5] |
ZHAO X L, NING D Z. Experimental investigation of breakwater-type WEC composed of both stationary and floating pontoons[J]. Energy, 2018, 155: 226-233. DOI:10.1016/j.energy.2018.04.189 |
| [6] |
CHEN Wenchuang, ZHANG Yongliang, YANG James, et al. Experiments and CFD modeling of a dual-raft wave energy dissipator[J]. Ocean Engineering, 2021, 237.
|
| [7] |
张恒铭. 波能装置与浮式防波堤集成系统的水动力特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [8] |
GODA Y, SUZUKI T. Estimation of incident and reflected waves in random wave experiments[C]// Proceeding of 15th Coastal Engineering Conference, Hawaii, 1976: 828−845.
|
| [9] |
JIANG S C, BAI W, TANG G Q. Numerical simulation of wave resonance in the narrow gap between two non-identical boxes[J]. Ocean Engineering, 2018, 156: 38-60. DOI:10.1016/j.oceaneng.2018.02.055 |
| [10] |
孙士艳. 非线性规则波中波能转换装置的水动力特征与能量转化效率研究[D]. 哈尔滨: 哈尔滨工程大学, 2016
|
| [11] |
BUDAR K, FALNES J, A resonant point absorber of ocean-wave power[J]. Nature,1975(8): 478−479.
|
 2023, Vol. 45
2023, Vol. 45
