随着信息技术和自动化控制技术的发展,越来越多的无人测量船采用了各种智能化的设备,从而可以大幅度提高测量船的测量准确度,同时也保障了船舶的行驶安全[1-3]。无人测量船是一种新兴的测绘装备,具有测量速度快、机动性强、工作环境好、无需专业设备等优点。因此,无人测量船在测绘领域有着广阔的发展空间。激光雷达系统已经在各种工业领域获得了长足的应用和发展,其测量精度高、速度快、距离远,因此在测量船感知系统中可以获得更加广泛的应用。本文研究无人测量船感知系统中的激光雷达技术的使用效果,建立相关的三维坐标模型,并优化了模型中的有关特征参数,大大提高了无人测量船的测量精度。
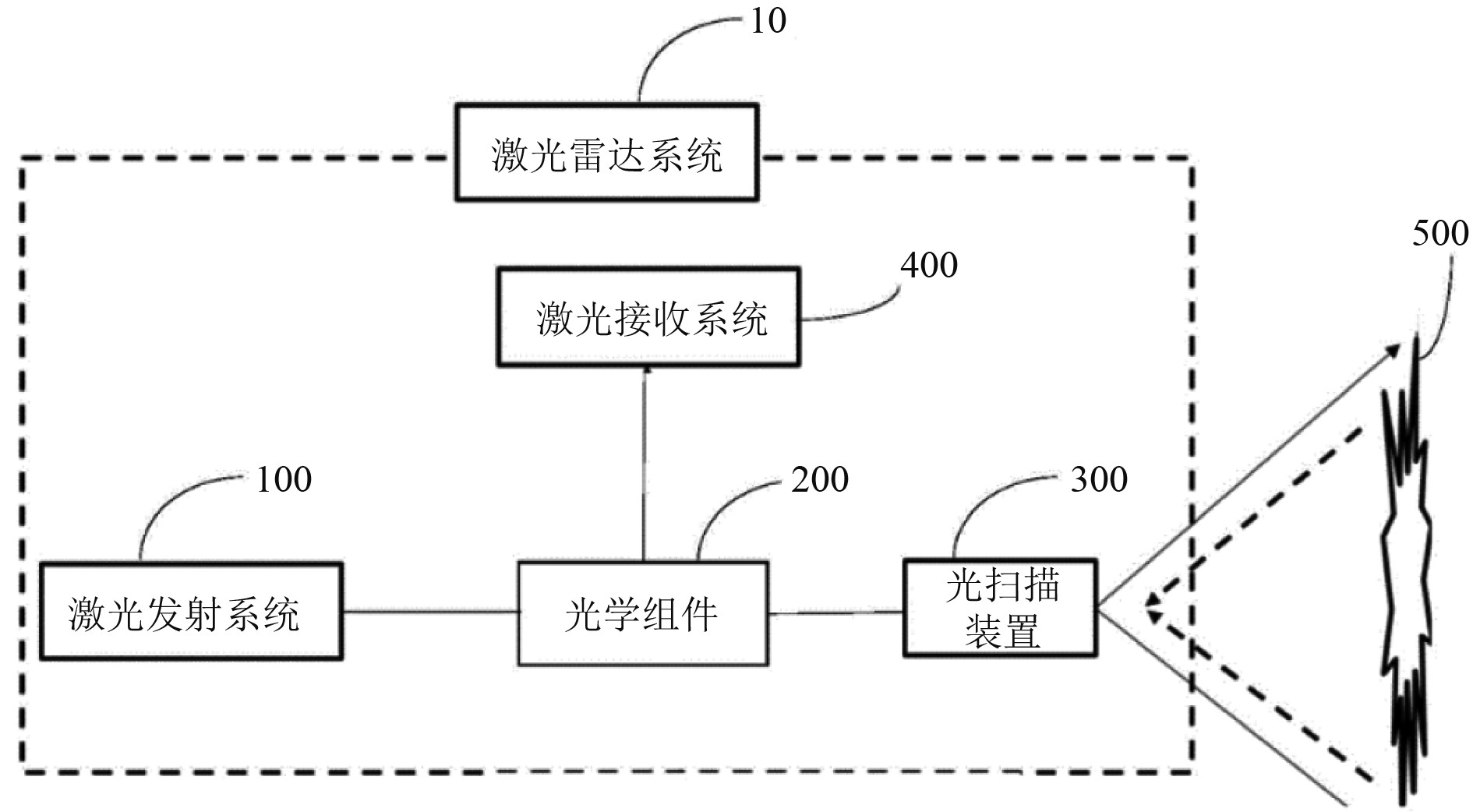
1 激光雷达技术激光雷达是一种用于探测环境或目标的激光测距、测速、航向和姿态测量的光电传感器,通过接收被测目标发射的激光脉冲,并测量其到达被测目标的距离来实现测量。激光雷达系统包括激光发射系统、激光接收系统、光学组件和光扫描装置等部分(图1为激光雷达系统图)。发射系统由激光器、光学系统和电子系统组成[4-6]。
|
图 1 激光雷达系统图 Fig. 1 Lidar system diagram |
激光雷达是一种具有全天候作业能力的测量仪器,其工作原理是基于发射与接收之间的时间延迟,测量所需的距离,通过接收并分析目标反射回来的激光脉冲信号来实现测量,是目前应用最广泛的一种激光测距仪,计算负载转矩的推导流程如下:
| $ {T_i} = \left( {\frac{{F \cdot {p_n}}}{{2\text{π} \eta }} + \frac{{{u_0}{F_A} \cdot {F_B}}}{{2\text{π} }}} \right) \cdot \frac{1}{\text{π} } \text{,} $ |
其中的切削负载转矩为:
| $ {T_{{m_s}}} = {T_c}{D^{\frac{1}{2}}} \leqslant {T_{{m_s}}} \cdot 80\% ,n = \frac{{{v_{\max }}U}}{{{p_n}}} \cdot {10^3} \leqslant {n_{{n_0}m}} ,$ |
由此得出T1与T2:
| $ {T_1} = \frac{{mv_2^2}}{{2 \times {{10}^6}}} ,{T_2} = \frac{{{J_{\omega o}}{\omega ^2}}}{2} \text{。} $ |
而基于动能守恒定律并结合以上相关公式,直线运动物体变换到电机中的负载惯量:
| $ {J_{\omega o}} = \frac{{mv_2^2}}{{{\omega ^2} \times {{10}^6}}} \text{。} $ |
与此同时,激光雷达还能够检测到周围环境中反射回来的光强分布,因此可以使用激光雷达来进行测距或测速。在无人测量船感知系统中使用激光雷达技术具备分辨率高、体积小、质量轻、抗干扰能力及低空探测能力突出的优势。
2 感知系统工作原理无人测量船感知系统通过激光雷达传感器对周围环境进行探测,并将数据传输至工控机。激光雷达传感器通过发射脉冲激光,在接收到回波信号后,对信号进行处理,将回波信号中的目标信息进行提取。在获取到目标信息后,该传感器会将接收到的信号和处理后的信息发送至工控机,而后者则基于接收到的信号进行处理,得到目标物体的位置信息、回波信息和方位信息。
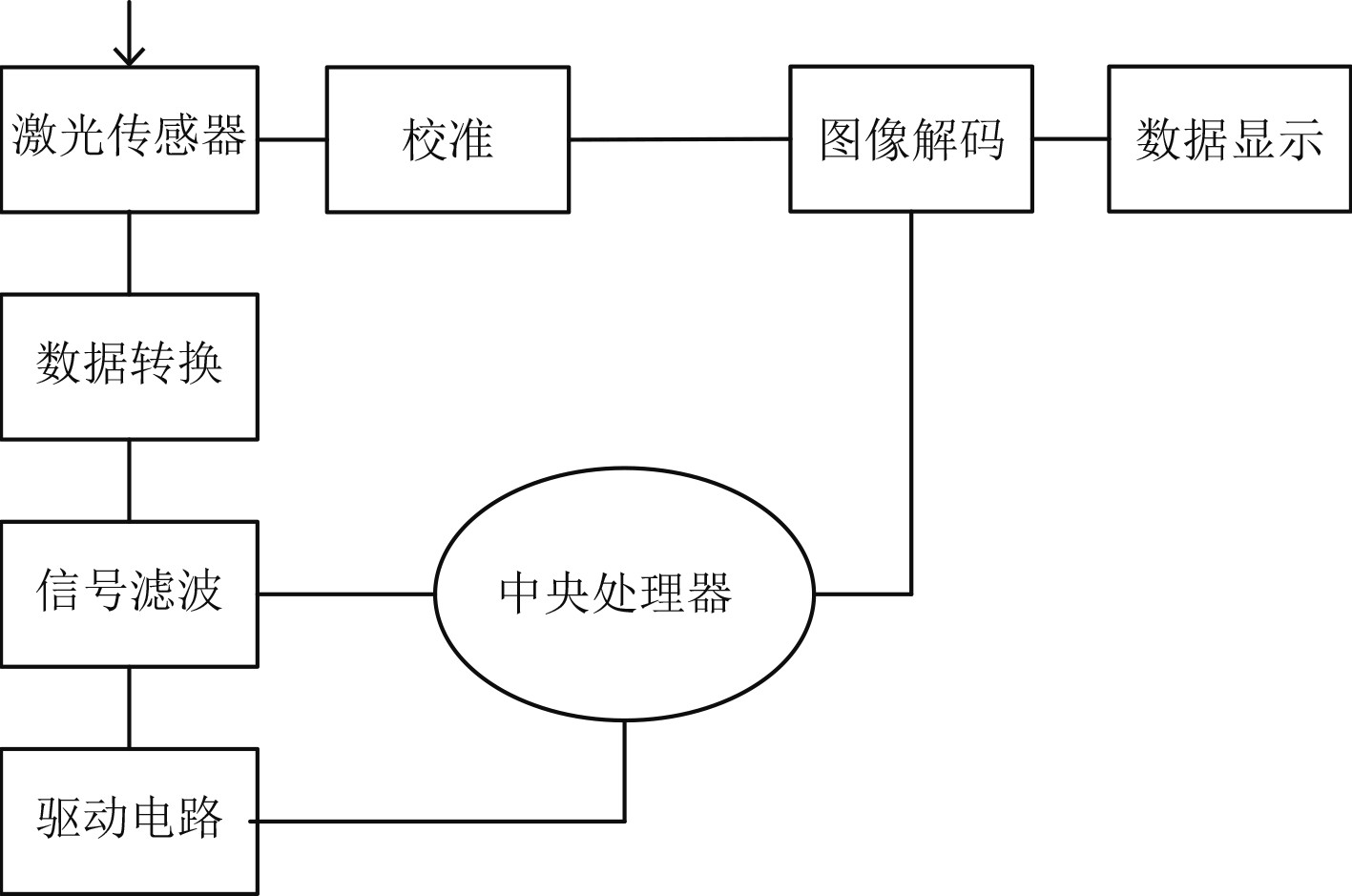
如图2所示,采用RS232和RS485总线对激光雷达传感器和工控机进行数据传输,使其能够有效地实现数据采集和传输,设计一种基于激光雷达传感器、工控机和以太网相结合的感知系统。
|
图 2 感知系统工作原理 Fig. 2 Operating principle of perception system |
传感器获取到的激光回波信号通过RS232总线传送至工控机,工控机将接收到的数据进行处理后,将数据通过以太网传输至传感器。因此,在感知系统中使用激光雷达传感器和工控机,能够有效提高感知系统在测绘作业过程中信息传输的安全性,解决无人测量船在测绘作业过程中信息传输存在安全隐患的问题。
3 激光雷达系统在无人测量船感知系统应用分析 3.1 外参模型以三维激光雷达为例,激光雷达不等同于其他光学相机等设备,需要通过外参标定,但其外部的参数标定也仅是为了获得更加精确的坐标系。
外部参考坐标的校准包括2个步骤:
第1步,仅围绕侧滚角的偏移入手展开分析,据此选择一个实际平面上的平面点,通过拟合法得到与其对应的旋转矩阵Rtemp;
第2步,采取人工设定校准位置,得到包含偏航角的原始数据,然后以此算出真实数据,再将两者进行比较,最后得到三维激光雷达坐标系统中的偏航角度θh°。在校准过程中,将三维雷达的Y轴方向设定为船首方向,并最终得到了旋转矩阵RLidar,如下式:
| $ R_{Lidar} = R_{temp}\left[ {\begin{array}{*{20}{c}} {\cos \left( {{\theta _h}} \right)}&{\sin \left( {{\theta _h}} \right)}&0 \\ { - \sin \left( {{\theta _h}} \right)}&{\cos \left( {{\theta _h}} \right)}&0 \\ 0&0&1 \end{array}} \right] \text{。} $ |
针对海上无人船不能维持其稳定的问题,提出一种基于雷达感知技术的无人船,将其放置在平静的海面上,以确保其稳定,并对其进行外部参数校准。与此同时,考虑到激光雷达的物理特性,对激光雷达进行水平校正。
利用水准仪使其处于水平线上,在不考虑偏航角度的情况下,构建三维直角坐标系统,坐标系为XSYSZS,并对该系统进行验证。
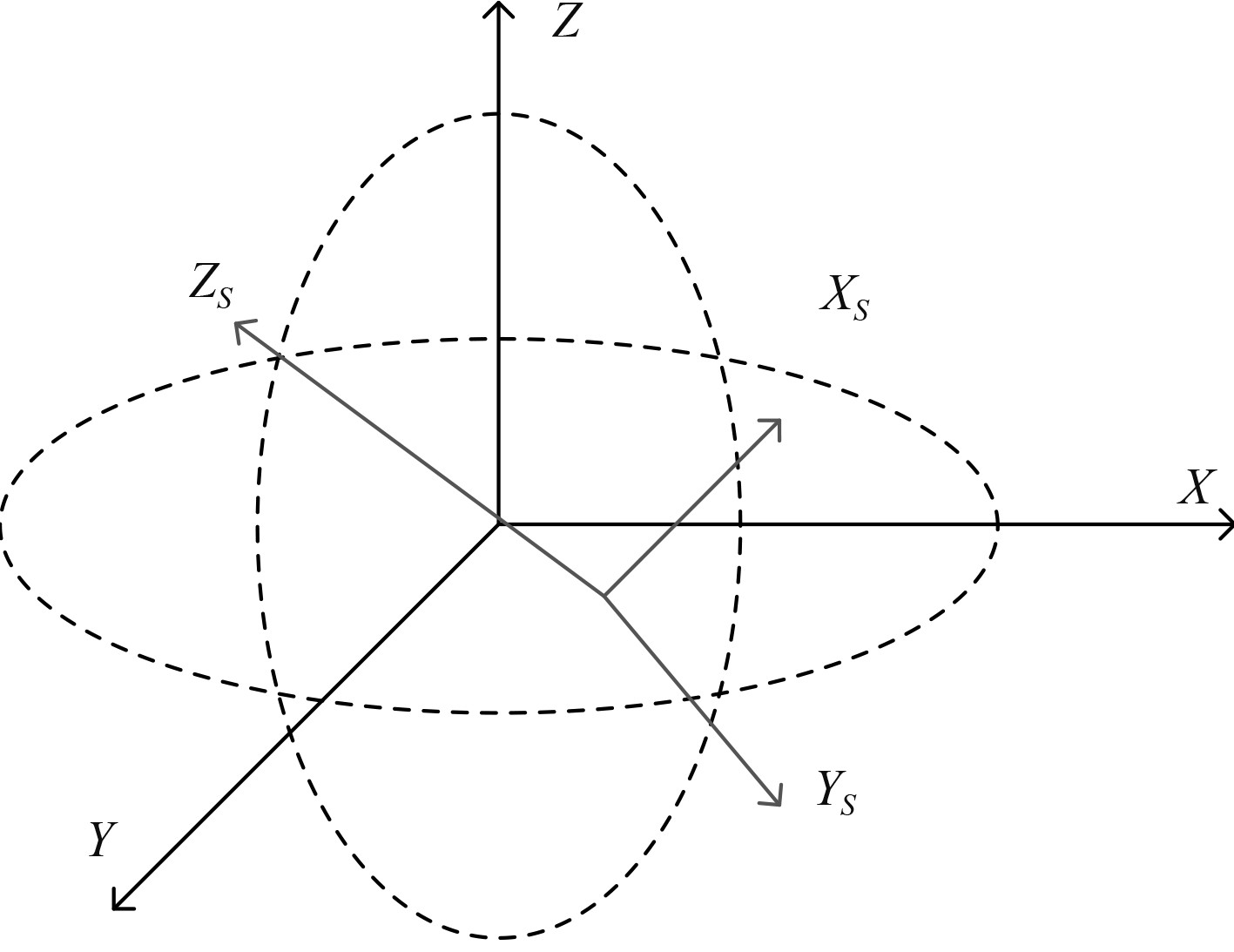
图3为本文研究的欧拉角示意图,通过将测量到的信息与实测数据进行结合,得出欧拉角。
|
图 3 欧拉角示意图 Fig. 3 Schematic diagram of Euler angles |
而平面法向量为n,如下式:
| $ n = \left( { - A, - B,I} \right) \text{,} $ |
变换后得到的坐标角如下式:
| $ \alpha = \frac{{{{\vec X}_s} \cdot \vec N}}{{\left| {{{\vec X}_s}} \right| \cdot \left| {\vec N} \right|}} ,\beta = \frac{{{{\vec Z}_L} \cdot {{\vec Z}_S}}}{{\left| {{{\vec Z}_L}} \right| \cdot \left| {{{\vec Z}_S}} \right|}} ,\gamma = \frac{{{{\vec X}_L} \cdot \vec N}}{{\left| {{{\vec X}_L}} \right| \cdot \left| {\vec N} \right|}}。$ |
其中:α为x轴与交点线N的夹角;β为Z轴与ZL轴的交点;γ为交点线N与XL轴的夹角。
最后由上式结合欧拉变化得出忽略偏航角的旋转矩阵:
| $\begin{aligned} {R_{Lidar}} = &\left[ {\begin{array}{*{20}{c}} {\cos \gamma }&{\sin \gamma }&0 \\ { - \sin \gamma }&{\cos \gamma }&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \beta }&{\sin \beta } \\ 0&{ - \sin \beta }&{\cos \beta } \end{array}} \right]\\ & \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha }&0 \\ { - \sin \alpha }&{\cos \alpha }&0 \\ 0&0&1 \end{array}} \right] 。\end{aligned}$ |
在船体周边5~20 m的区域进行了区间划分,再每间隔5 m画出一条与船体平行或垂直的直线,将其组成8×8的网格进行水平面。
每2条直线相交的地方,确定为辅助标定的标尺,并且以此为依据进行逆向推算,这样无人船水平面移动误差可以显著降低,将其代入到如下误差公式中:
| $ E\left( R \right) = {\left\| {R * {P_{i - {P_i}}}} \right\|^2}。$ |
将航向角误差和水平误差进行一个标定,如下式:
| $ E\left( R \right) = \sum\limits_i {\left( {{R^2}P_i^2 - 2{p_i}R{P_i} + P_i^2} \right)} = \sum\limits_i {\left( {{p_i}R{P_i}} \right)} \text{,} $ |
根据立体几何原理,三维矩阵可以用一定的矢量和矢量转动角度来表达。即由4个变量组成三维转动矩阵。基于此,引进了一个四元q:
| $ q = \left[ {{q_1},{q_2},{q_3},{q_4}} \right] \text{,} $ |
其中q为一个系统坐标结合体,通过对其进行分析,可以得出R和q之间的关系如下:
| $ R = \left[ {\begin{array}{*{20}{c}} {q_0^2 + q_1^2 + q_2^2 + q_3^2} & {2\left( {{q_1}{q_2} - {q_0}{q_3}} \right)} & {2\left( {{q_1}{q_3} + {q_0}{q_2}} \right)} \\ {2\left( {{q_1}{q_2} + {q_0}{q_3}} \right)} & {q_0^2 - q_1^2 + q_2^2 + q_3^2} & {2\left( {{q_2}{q_3} - {q_0}{q_1}} \right)} \\ {2\left( {{q_1}{q_3} - {q_0}{q_2}} \right)} & {2\left( {{q_2}{q_3} + {q_0}{q_1}} \right)} & {q_0^2 - q_1^2 + q_2^2 + q_3^3} \end{array}} \right] \text{,} $ |
| $ {R_{{p_i}}} = q{p_i}q * \text{,} $ |
| $ E'\left( R \right) = \sum\limits_i {{p_i}} R{P_i} = {q^{\rm{T}}}\left( {\sum\limits_i {p_i^{\rm{T}}{P_i}} } \right)q。$ |
对矩阵求解可以得出最小特征值所对应的特征向量q,从而得到无人船的运行特征值为:
| $ {T_b} = \frac{1}{N} \cdot \sum\limits_{i = 1}^N {{P_i}}。$ |
三维激光雷达:
| $ {T_L} = \frac{1}{N} \cdot \sum\limits_{i = 1}^N {{P_i}} \text{,} $ |
以及x-y平面的水平位移矩阵:
| $ {T_{XSYS}} = {T_b} - R * {T_L} 。$ |
最后得到外参校正的平移矩阵C满足下述方程:
| $ A{X_S} + B{Y_S} - Z + C = 0 。$ |
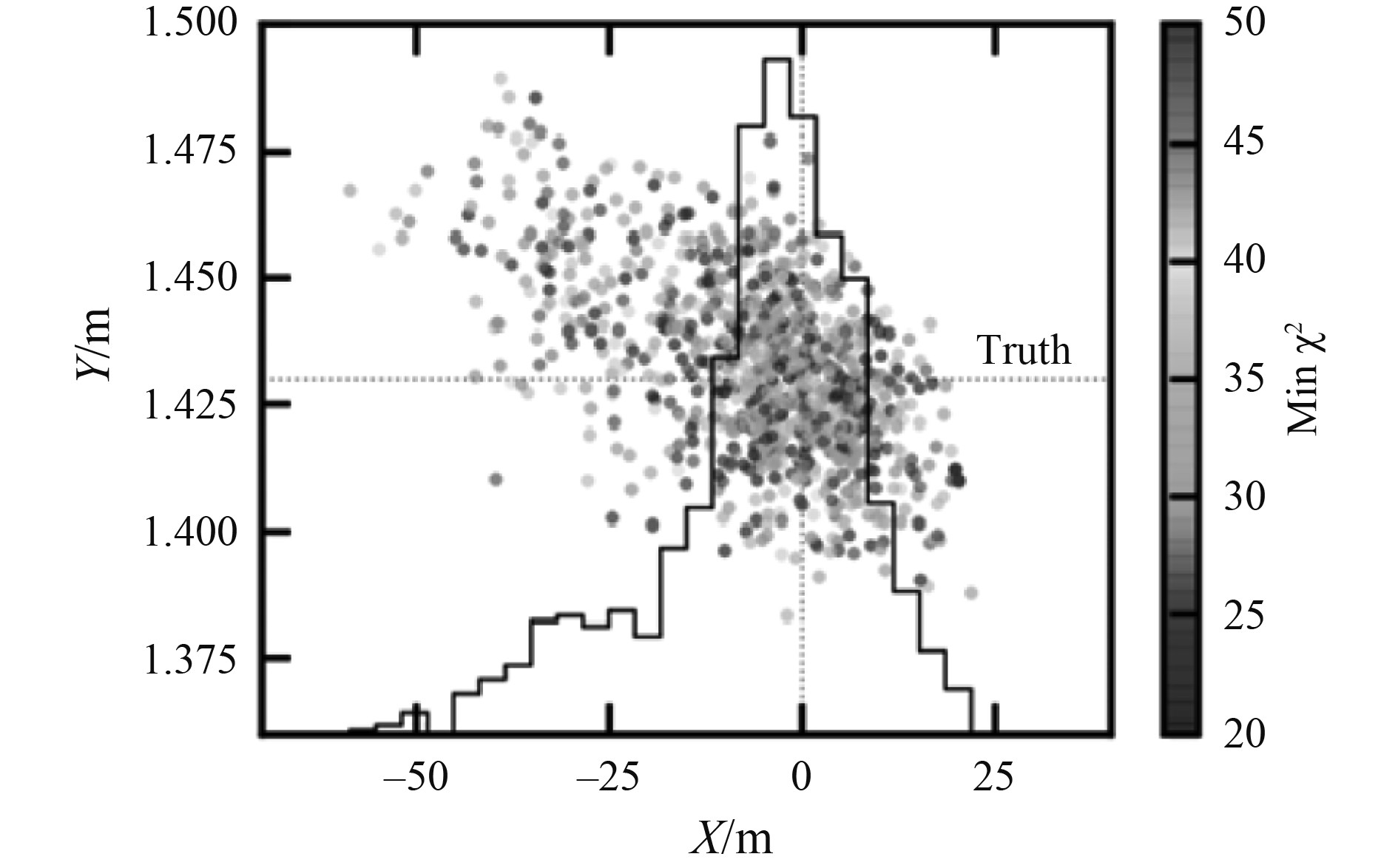
由此可以得出激光雷达坐标系的转换。目标反射物的坐标分布图如图4所示。
|
图 4 目标反射物的坐标分布图 Fig. 4 Coordinate distribution map of target reflector |
在真实的海上行驶中,由于舰船的摇摆是由两个不同的倾斜角度引起的,因此为了增加激光雷达的探测精度,必须对其进行横向和纵向的修正。利用姿态补偿器测得船舶的纵倾及横倾,并以测得的数据为基础对船舶坐标进行校正。
将船舶的横纵角设定为α,将纵向倾角设定为β,从而可以得到测量值(Pxs, Pys, Pzs)与水平坐标系中的(x,y,z)的关系,如下式:
| $\begin{aligned} \left[ {\begin{array}{*{20}{c}} {x'} \\ {y'} \\ {z'} \end{array}} \right] =& Tl\left( a \right)\left[ {\begin{array}{*{20}{c}} {{P_{xs}}} \\ {{P_{ys}}} \\ {{P_{zs}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \alpha }&{\sin \alpha } \\ 0&{ - \sin \alpha }&{\cos \alpha } \end{array}} \right]\times\\ & {\left[ {\begin{array}{*{20}{c}} {{P_{xs}}} \\ {{P_{ys}}} \\ {{P_{zs}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{P_{xs}}} \\ {{P_{ys}}\cos \alpha + {P_{zs}}\sin \alpha } \\ { - {P_{ys}}\sin \alpha + {P_{zs}}\cos \alpha } \end{array}} \right],}\end{aligned} $ |
| $\begin{aligned} \left[ {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right] = &{T_2}\left( \beta \right)\left[ {\begin{array}{*{20}{c}} {x'} \\ {y'} \\ {z'} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \beta }&0&{ - \sin \beta } \\ 0&1&0 \\ {\sin \beta }&0&{\cos \beta } \end{array}} \right]\times \\ & {\left[ {\begin{array}{*{20}{c}} {x'} \\ {y'} \\ {z'} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {x'\cos \beta - z'\sin \beta } \\ y \\ {x'\sin \beta + z'\cos \beta } \end{array}} \right] 。} \end{aligned}$ |
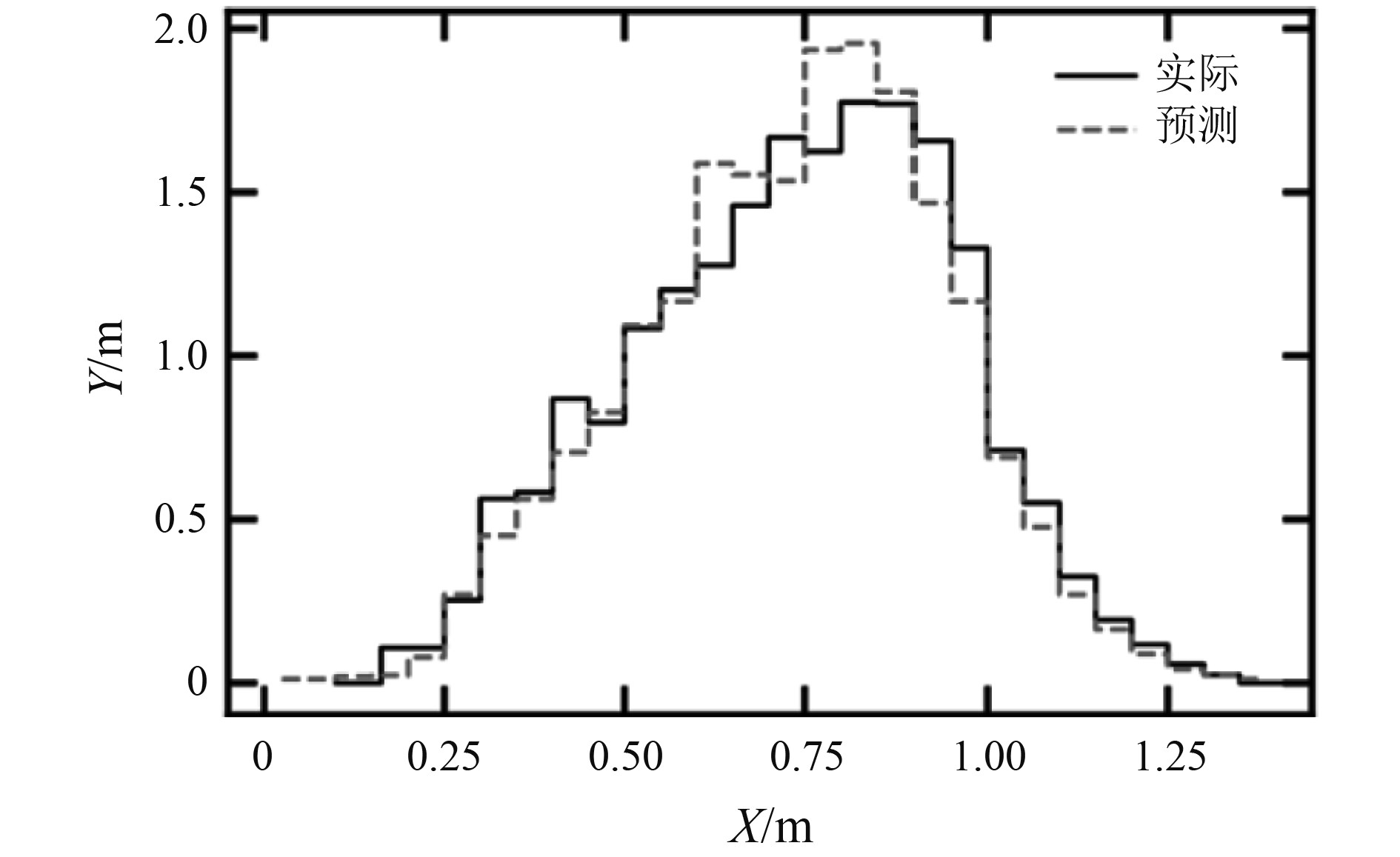
结合以上,最终可以得到激光雷达探测点坐标(x,y,z)。其中,坐标位置的激光雷达探测精度如图5所示。
|
图 5 激光雷达探测精度 Fig. 5 LiDAR Detection Accuracy |
将激光雷达技术应用于无人测量船感知系统中,其具体步骤如下:
1)将激光雷达传感器安装至无人测量船的船体两侧;
2)使用工控机作为控制中心,并将以太网和RS232/RS485标准总线相结合,将所获取到的数据传输至工控机;
3)使用工控机对激光雷达传感器采集到的数据进行处理,包括滤波、计算目标距离信息、计算目标角度信息等;
4)将处理后的数据传输至工控机,并在工控机中显示出目标物体在不同状态下的三维坐标。同时,可以通过控制中心控制激光雷达传感器的运行状态。
5 结 语本文提出一种基于激光雷达技术的无人测量船感知系统,该系统以三维激光雷达技术为例,通过和工控机相结合的方式进行数据采集和处理。通过对激光雷达采集的数据进行分析,可以得出以下结论:
1)基于激光雷达的感知系统,其在对无人测量船进行测量时,可以通过在无人测量船上使用传感器来实时进行信息更新,获取船只周围的地形、地貌信息等,有效地提高无人测量船信息传输的安全性,将航行安全风险问题降至最低;
2)通过对采集到的数据进行误差处理,得到更为精确的三维坐标系,能够得到无人测量船感知系统在作业过程中所需要的各个要素的三维空间位置,并且将数据进行可视化处理。
| [1] |
戴云峰, 丁亚杰, 冯兴明, 等. 基于EPnP算法的激光雷达与可见光相机标定方法[J]. 光电子技术, 2023, 43(2): 166-172. |
| [2] |
梁冲. 基于机载LiDAR与无人船多波束的水陆一体化测量技术研究[J]. 水利技术监督, 2022, 176(6): 70-74. |
| [3] |
王锴磊, 郭力振, 朱浩, 等. 智能导航多线激光雷达校准方法研究[J]. 测试技术学报, 2023(5): 381-385+393. |
| [4] |
毛松, 步志超, 陈玉宝, 等. 大气激光雷达气溶胶光学参数质量可信度评估算法[J]. 气象科技, 2023, 51(3): 309-318. DOI:10.19517/j.1671-6345.20220418 |
| [5] |
刘冰洋. 无人船辅助激光雷达在跨河测量中的应用[J]. 铁道勘察, 2021, 47(3): 43-47. |
| [6] |
尚业华, 王昊, 孟志军, 等. 基于激光雷达的稻麦收获边界检测与自动对齐系统研究[J]. 农业机械学报, 2023, 54(5): 19-28+46. DOI:10.6041/j.issn.1000-1298.2023.05.002 |
 2023, Vol. 45
2023, Vol. 45
