船舶管路是船舶上用来连接各种机械设备的管道,用来传送水、油、气等有关工质,管路振动噪声是船舶主要噪声源。泵是管路系统中重要振源之一,随着浮筏、气囊隔振等技术的应用,沿设备机脚传递到基座的振动得到明显改善,管路和管内介质通道成为振动主要传递途径。设备在复杂管路系统中工作,将在管道内产生压力脉动,当压力脉动变化频率与管道结构固有频率相近时,会引起管道系统共振,导致管道和管道附件松动和损坏,并产生振动和噪声,破坏舰船的隐蔽性和舒适性。
Vetter等[1]早已对压力脉动模型进行深入研究,王秋颖和周红等[2-3]也分别提出压力脉动模型,而基于流固耦合对管道振动的研究也已有丰富成果[4-6],但同时将压力脉动与管道振动二者结合起来的研究较少。熊雄等[7]提出压力脉动计算模型并应用到流固耦合瞬态力学分析,研究了异径管和弯管处压力变化和管道应力变形情况;窦益华[8]基于流固耦合研究了脉动频率对管道振幅的影响。关于压力脉动条件下输液管道振动特性仍有待进一步研究。
本文以某船舶管道系统为研究对象,通过Ansys有限元仿真软件,使用UDF方法将压力脉动加载到管道中进行双向流固耦合分析,研究压力脉动下管道系统振动特性。
1 管道振动的基本理论 1.1 结构动力学模型有限元法分析管系是通过离散化的方法用有限个自由度的离散系统代替无限个自由度的连续系统,管系振动微分方程的矩阵形式由下式表示:
| $ {\boldsymbol{M}}\left( {{x{''}}} \right) + {\boldsymbol{C}}\left( {{x'}} \right) + {\boldsymbol{K}}\left( x \right) = {\boldsymbol{F}}\left( t \right)。$ | (1) |
其中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;(x)为位移矢量;(
管路的模态包括固有频率和振型,一般情况下,在分析管路模态时可忽略阻尼的影响,由式(1)可得到管路系统无阻尼自由振动的方程。
| $ {\boldsymbol{M}}\left( {{x{''}}} \right) + {\boldsymbol{K}}\left( x \right) = 0。$ | (2) |
结构自由振动一般为简谐振动,假设管路的位移具有以下形式:
| $ x = X\sin \left( {\omega t + \varphi } \right) ,$ | (3) |
将式(3)代入式(2)中可得:
| $ \left( {{\boldsymbol{K}} - {\omega ^2}{\boldsymbol{M}}} \right)x = 0。$ | (4) |
式(4)有非0解的充要条件是系数行列式为0,即
| $ \left| {{\boldsymbol{K}} - {\omega ^2}{\boldsymbol{M}}} \right| = 0。$ | (5) |
式(5)为多自由度问题的频率方程,它具有n个根ω21,ω22…ω2n。其中ωi是系统的第i阶固有频率,n为系统自由度。将n个固有频率代入式(4)中,可求得n个特征向量(x)1,(x)2…(x)n,即为系统的振型。
1.2 压力脉动模型管路内压力脉动是极其复杂的现象,随着计算机技术的发展及计算方法的改进,对压力脉动的研究经历了由简单到复杂、由粗糙到精确的过程。从忽略阻尼到计及阻尼,从线性阻尼到更接近实际的非线性阻尼;从不计流速到考虑平均流速;从限于小波动到有限幅波动,以至计及热交换的情况,考虑的因素越多,越接近实际过程,但处理相应的力学模型和数学方程的求解也更复杂。在无阻尼,小波动情况下,压力脉动模型为:
| $ {P_\vartriangle }\left( {x,t} \right) = \left[ {{C_n}\cos {\omega _n}t + {D_n}\sin {\omega _n}t} \right]\sin \left( {\frac{{n\text{π} x}}{l}} \right) 。$ | (6) |
其中:
| $ {C_n} = \frac{{ - 2{\text{p}}}}{{n\text{π} }}\left( {\cos n\text{π} l - 1} \right) ,$ | (7) |
| $ {D_n} = \frac{{ - 2u}}{{{n^2}{\text{π} ^2}cl}}(\cos n\text{π} l - 1)。$ | (8) |
式中:
则管路内压力可表示为静压力分量与脉动压力分量之和:
| $ P = {P_0} + {P_\Delta }\left( {x,t} \right) 。$ | (9) |
流固耦合分析(Fluid-Structure Interaction Analysis)是将流体特性分析和固体结构分析交叉耦合形成的分析方法,主要研究固体结构在流场作用下的各种结构特性及固体变形对流场特性反作用的影响。流固耦合在分析问题时,同时考虑了流体和固体结构特性,其分析结果要比单独的流场分析或固体结构分析更真实可靠。
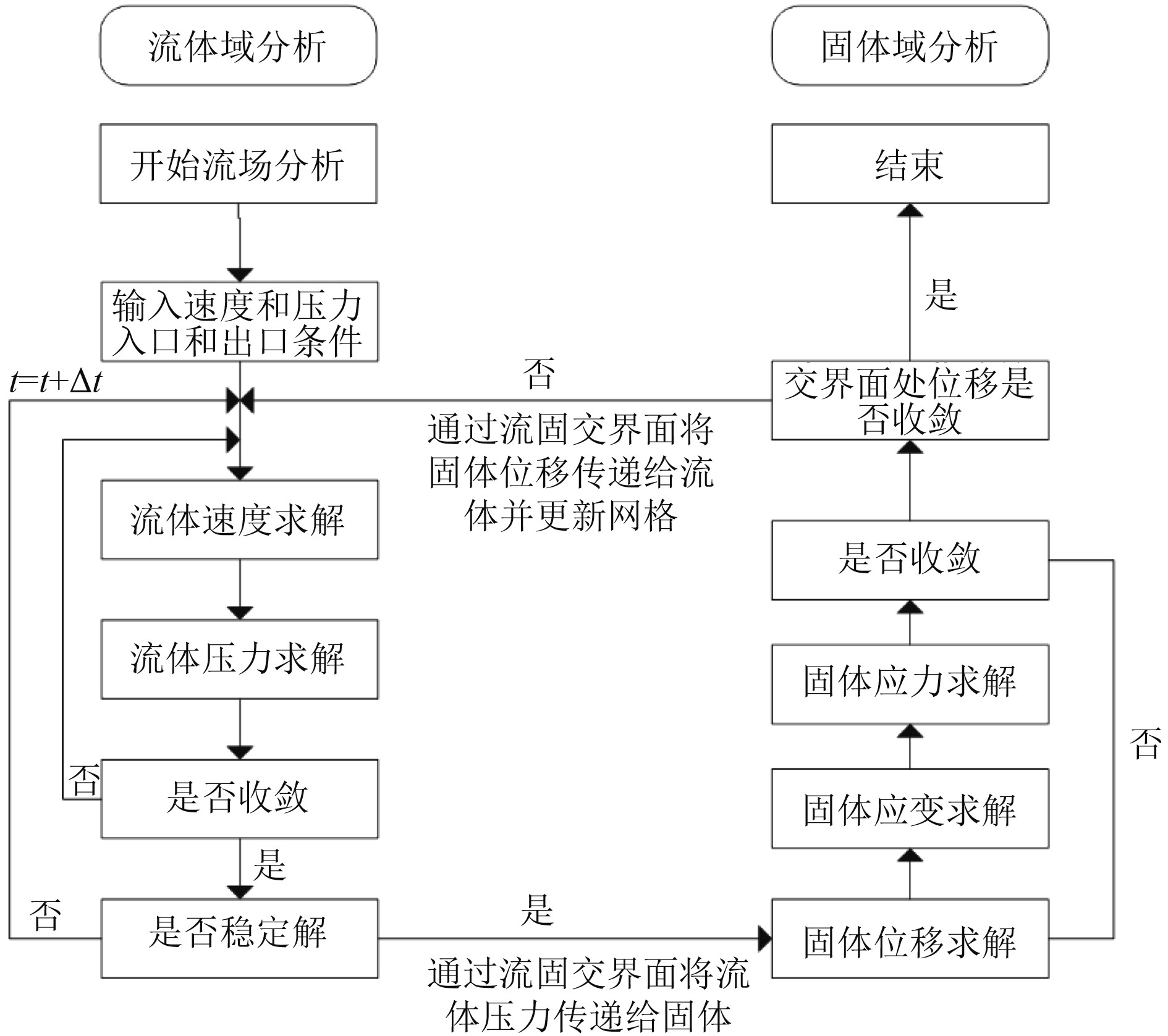
根据耦合的方式可将流固耦合分为顺序耦合和直接耦合2种类型,按照顺序耦合计算时先分别计算不同的物理场,把先得到的结果作为载荷施加到另一个场进行计算,根据数据传递的路径,顺序耦合又可分为单向耦合和双向耦合。单向耦合只将流体分析结果(如压力温度、对流载荷等)传递给固体结构分析,只考虑了流体对结构的作用,忽略了固体结构对流体的影响,适用于只考虑静力学特性的影响,研究管路系统振动等动力学特性时,必须使用双向耦合方式。
|
图 1 双向流固耦合算法流程图 Fig. 1 Flow chart of bidirectional fluid solid coupling |
|
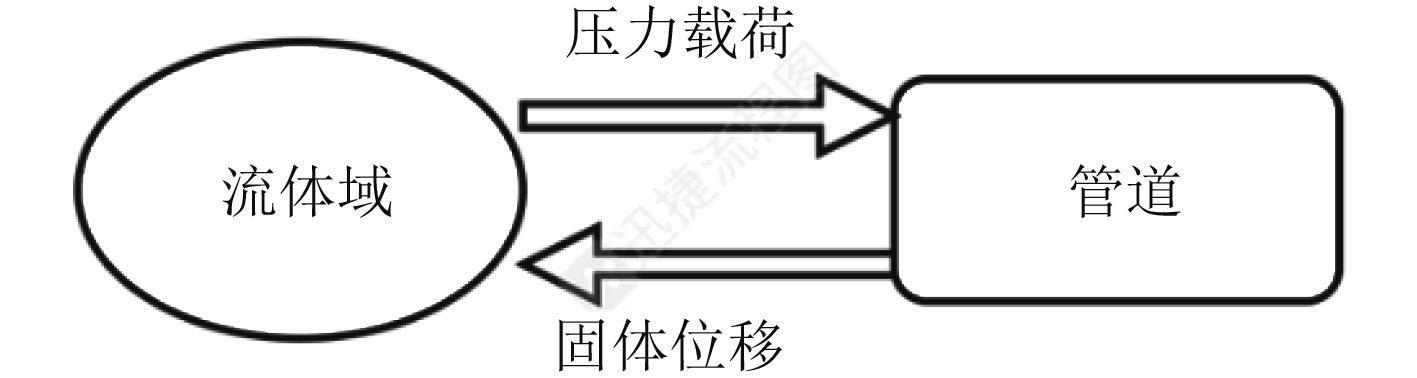
图 2 双向耦合数据传递 Fig. 2 Bidirectional coupling data transfer |
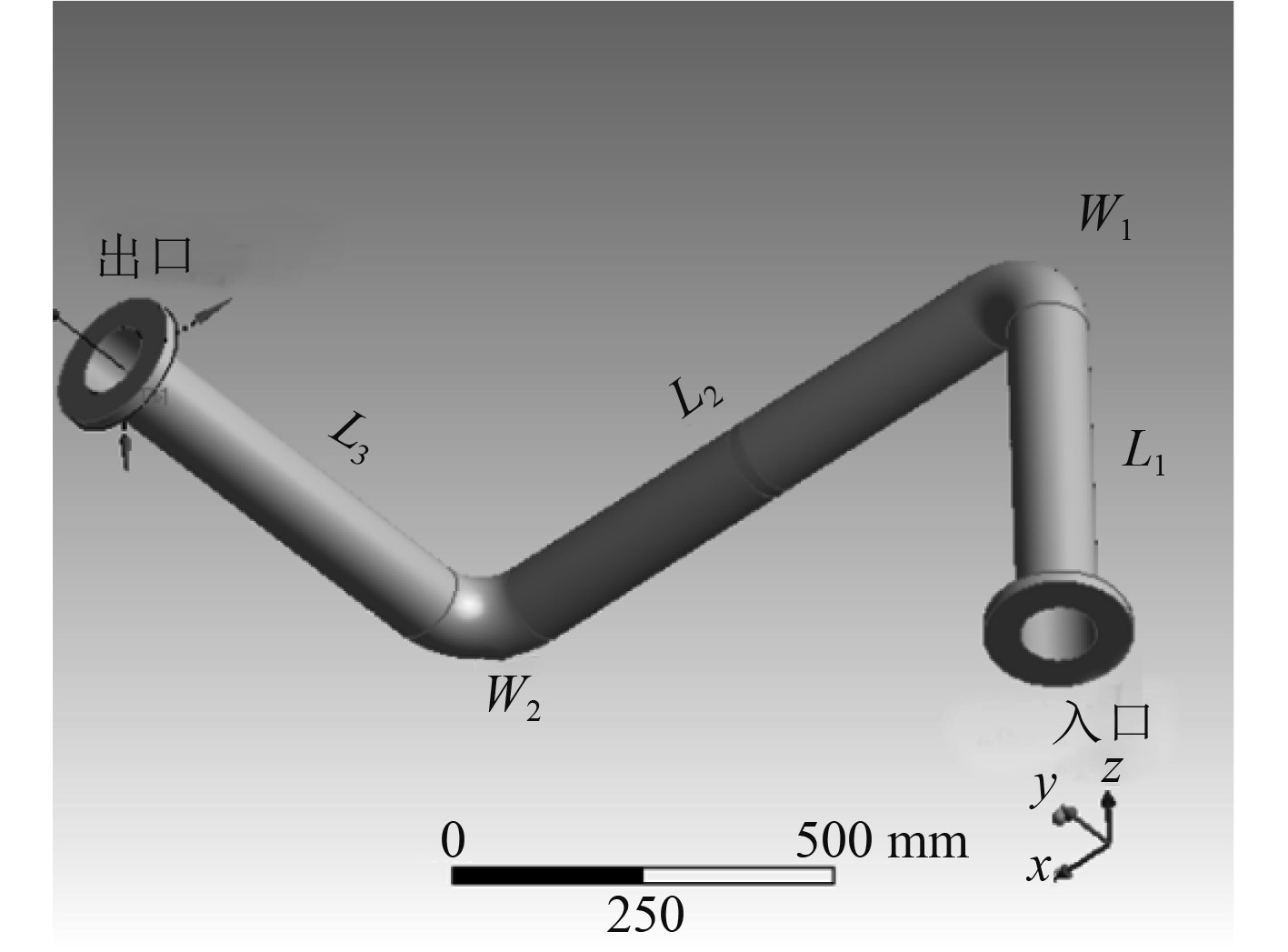
实验台架选取出口段管路3段直管、2段弯管建立三维模型,如图3所示。管路外径D = 108 mm;内径d = 100 mm;壁厚δ=4 mm;直管段L1=535 mm,L2=800 mm,L3=600 mm;弯管段半径均为100 mm。管路材料为20号碳素钢,物理性能参数如表1所示,管内介质为20℃水。
|
图 3 管路系统几何模型 Fig. 3 Geometric model of pipeline system |
|
|
表 1 管路材料属性 Tab.1 Pipe material properties |
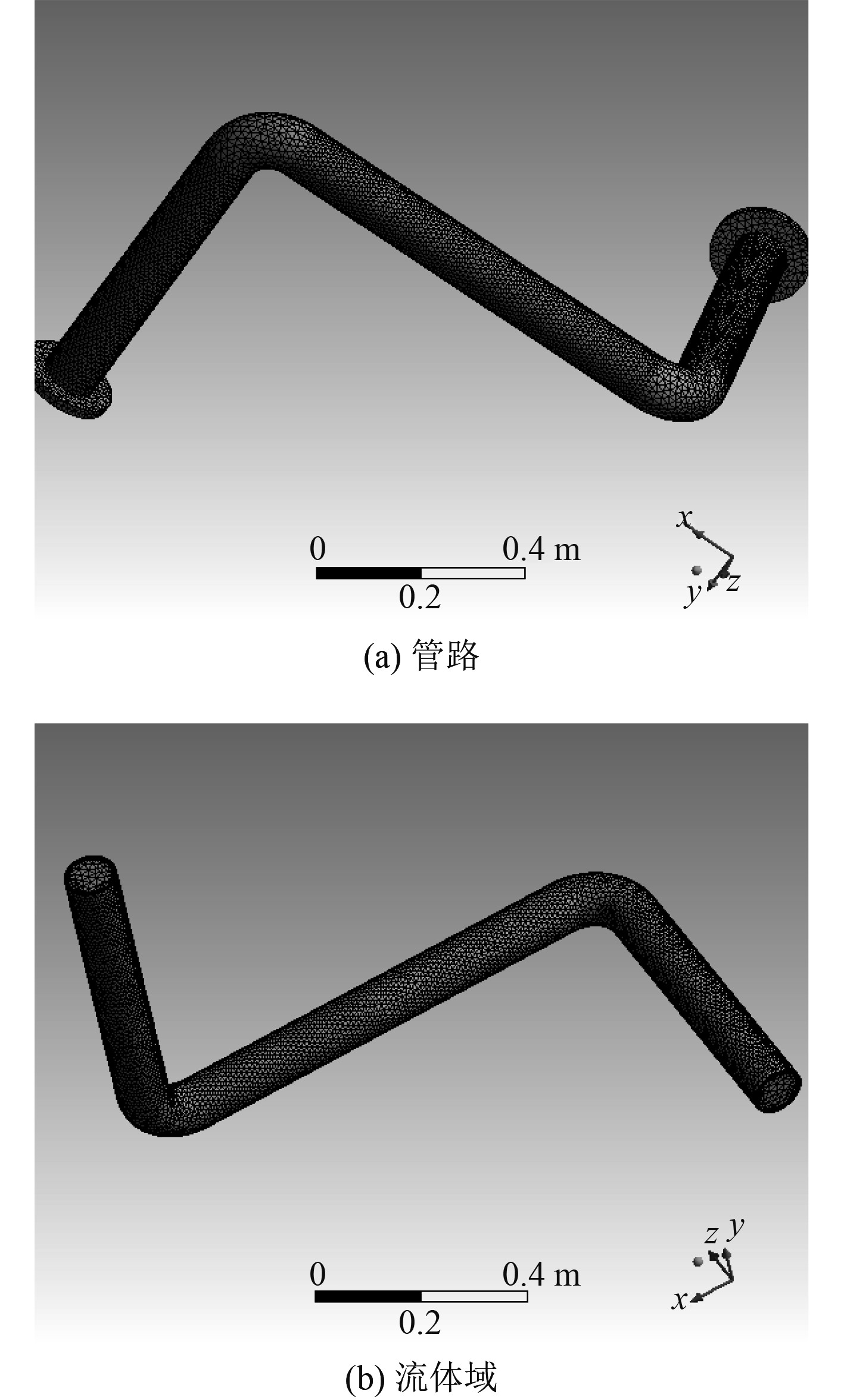
网格划分方案如图4所示,管路模型节点94883个,单元47593个,流体域节点54995个,单元151436个,并将管路内表面和流体域表面设置为流固耦合面。
|
图 4 网格划分方案 Fig. 4 Mesh generation scheme |
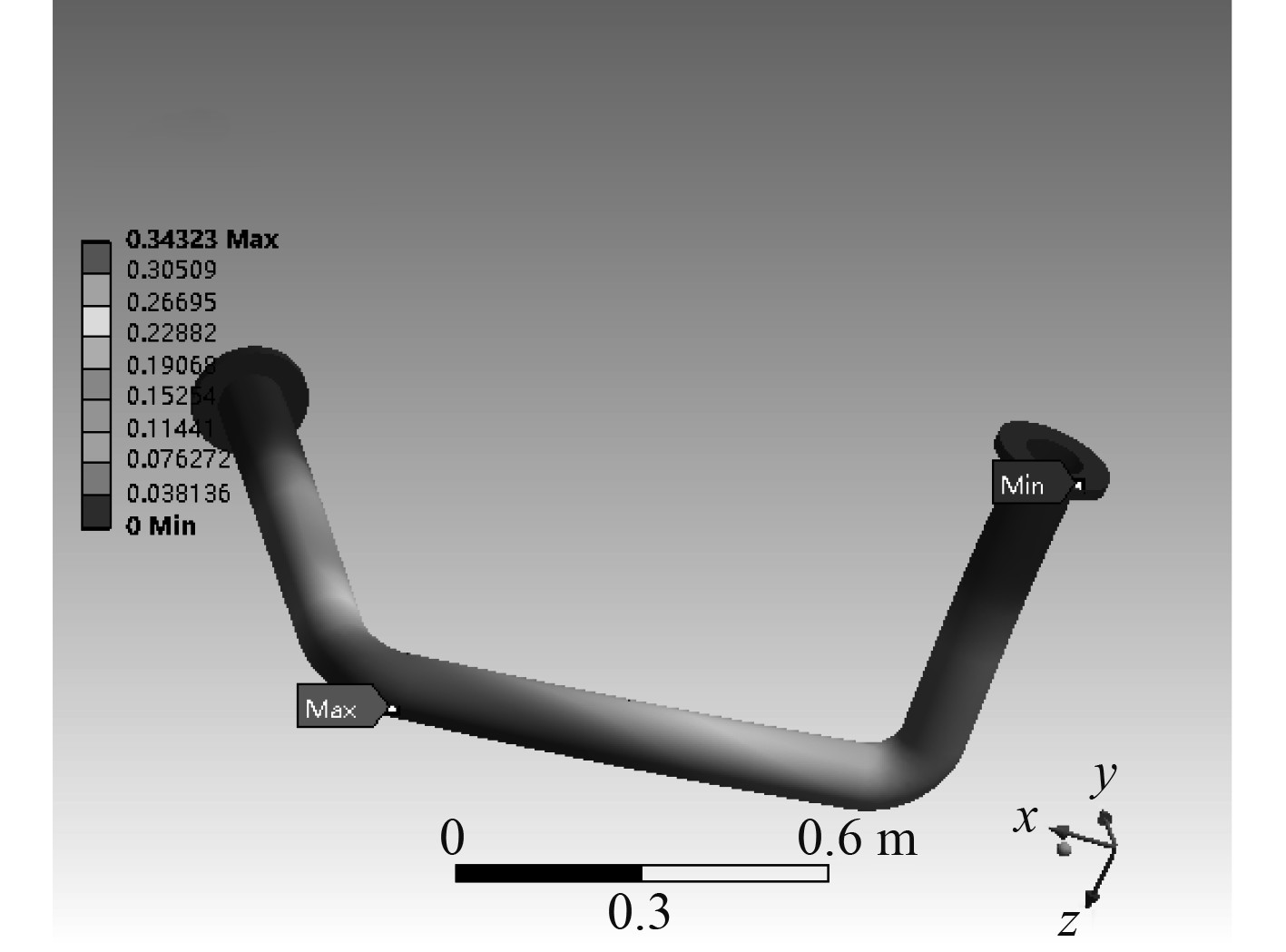
为了避免管路在固有频率和压力脉动频率相近时发生共振,有必要先对管路进行模态分析,模态分析可用来获得管路各阶固有频率,并且通过振型图可以看到管路各部分振动幅度以及各阶振型最大变形发生位置。抑制流体域后将管路模型导入modal模块,在法兰端面添加固定约束,提取前6阶固有频率如表2所示。一阶模态振型如图5所示,可以看出一阶模态振型变形最大部位在第一个弯管后管段附近。
|
|
表 2 管路前6阶模态 Tab.2 First six modes of pipeline |
|
图 5 管路第一阶模态振型 Fig. 5 First order modal mode of vibration |
当管路固有频率与激振力频率相近时,应当调整管路固有频率,避免共振。
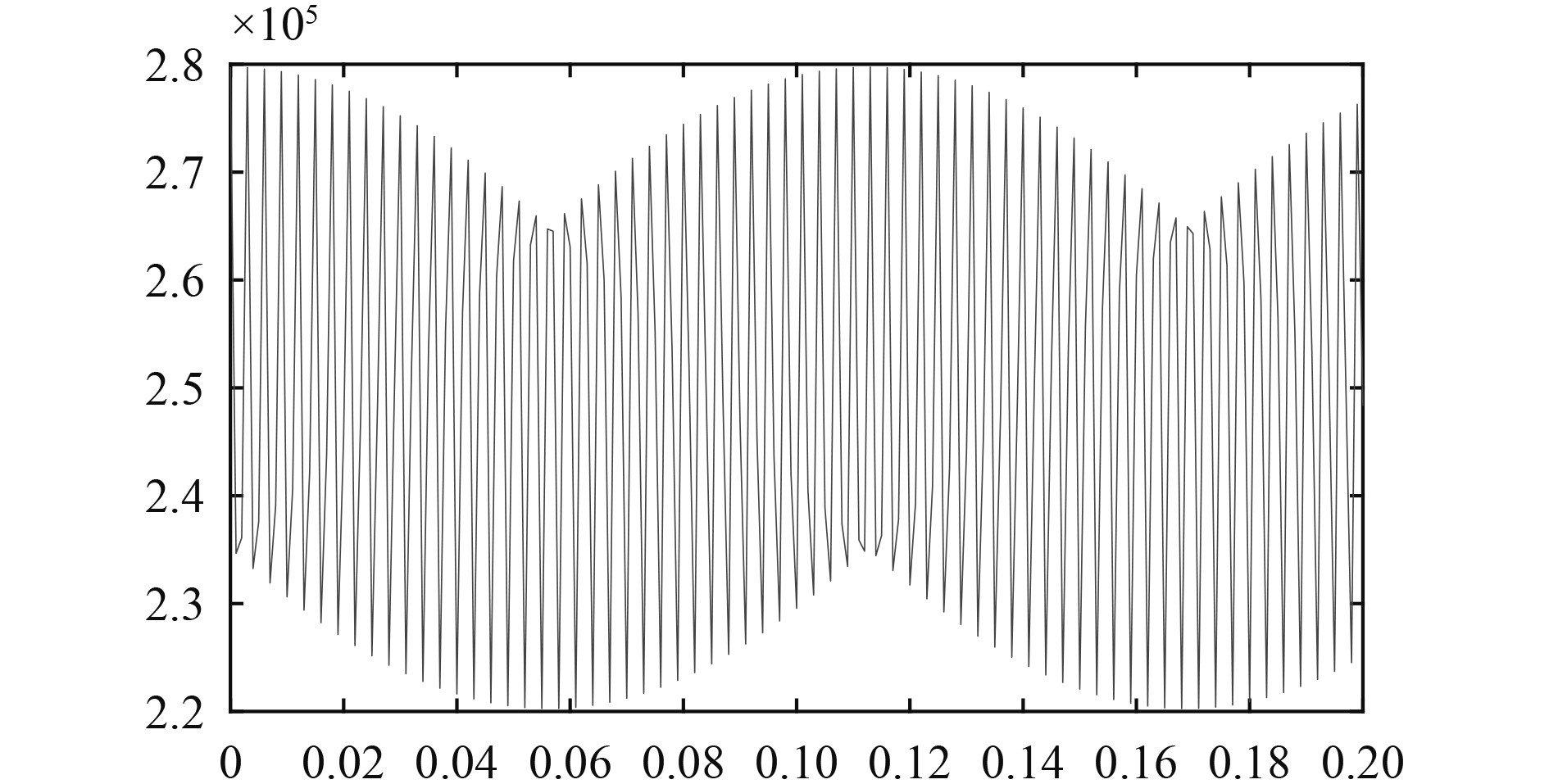
2.3 压力脉动加载根据式(7)和式(8)发现,Dn是个极小值且Dn<<Cn,为简化计算,忽略Dn项。结合台架管路条件,可将如下的压力脉动作为压力入口条件通过UDF的方式加载到入口边界上,波形图如图6所示。
|
图 6 管路内压力脉动波形 Fig. 6 Pressure fluctuation waveform in pipeline |
| $ P\left( t \right) = 250\;000 + 43\;620 * \cos (2\;113*{\text{t}}) * \sin \left( {0.75} \right)。$ | (10) |
其中,Cn=43620(初始压力p=250000 Pa,管路总长l=2249 mm),压力脉动的频率f = 336 Hz,距管路第3阶和第4阶固有频率较远,不会激发管路共振。
2.4 工况及耦合计算设置式(10)中的Cn在实际管路条件的基础上,结合式(6)计算得到,记为CT n,为充分研究压力脉动对管路振动问题的影响,改变CT n的数量级后重复计算,多种计算工况如表3所示。各工况中的Cn与CT n的比值记为k,k可清晰表示各工况脉动压力幅值变化的关系,各工况加载的压力脉动可以统一由下式表示:
|
|
表 3 工况表 Tab.3 Working condition setting |
| $ P\left( t \right) = 250\;000 + \left( {k \times 43\;620} \right) \times \cos (2\;113\times{\text{t}}) \times \sin \left( {0.75} \right)。$ | (11) |
监测进出口、直管处和弯管处的振动加速度,并进行FFT分析后得到各点振动总级,结果如表4所示。对比工况1~工况4可看出,当压力脉动远小于静压力时,工况1~工况4中管路的振动情况基本没有变化,此时压力脉动对管路振动的影响可忽略不计。从工况5~工况10可看出,当压力脉动增加时,管路各位置的振动也更为剧烈,其中L2处的振动最为剧烈。
|
|
表 4 不同位置振动总级La /dB Tab.4 Total vibration level at different positions |
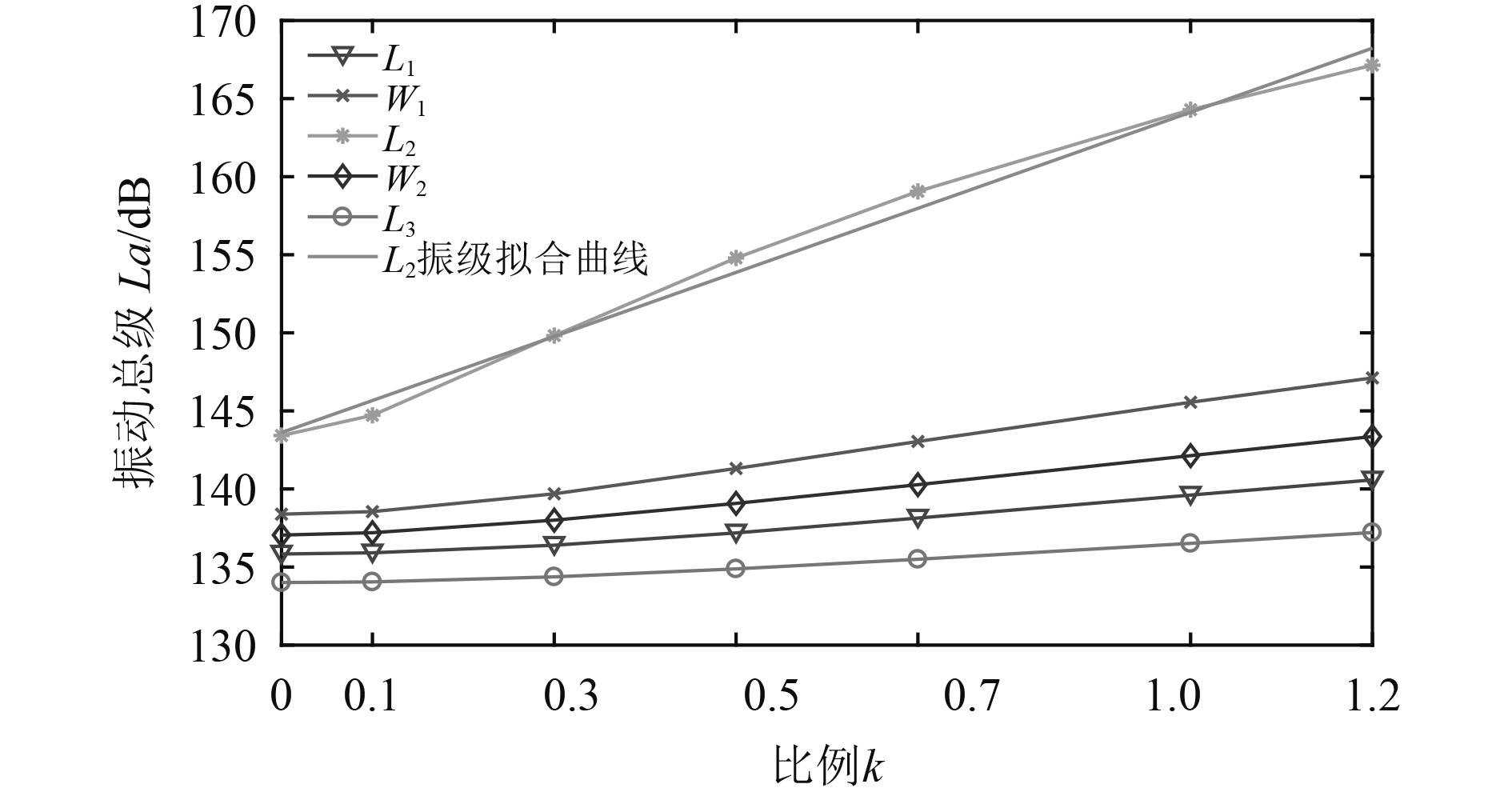
以比例k为x轴,振动总级La为y轴,工况1和工况5~工况10的管路振动情况如图7所示。可以看出,在简单管路条件下,振动加速度级和压力脉动之间存在近于线性的增长关系,其中L2处增长最快,即L2处受压力脉动的影响最大。对L2处振级和比例k作一阶最小二乘拟合,则L2处振动总级和压力脉动的增长关系可由式(12)表示。
|
图 7 不同压力脉动条件下管路振动情况 Fig. 7 Total vibration level of each position under different pressure pulsation conditions |
| $ La=20.5\ast k+143.6=20.5\ast \frac{\Delta p}{46320*\mathrm{sin}(0.75)}+143.6 。$ | (12) |
其中,
以工况1、工况9为例,对不同位置振动加速度级进行FFT处理后得到其在频域的分布情况,如图8所示。可以看出,相对工况1来说,工况9不同位置振动的高频分量增大,静压力对管路振动的影响主要集中在低频段,脉动压力分量主要影响高频段。

|
图 8 工况1、工况9不同位置振动频谱对比 Fig. 8 Comparison of frequency spectrum at different positions of working condition 1 and working condition 9 |
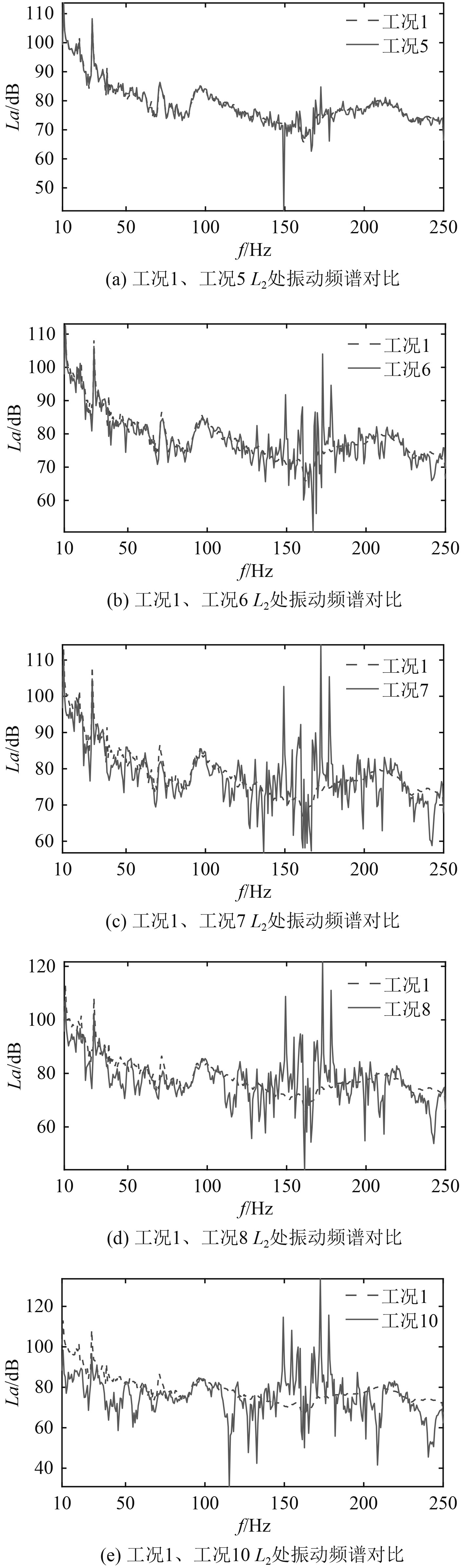
图8(c)中,较之工况1,工况9中L2处振动高频分量增大的同时,低频分量却在降低,分析其他工况L2处振动频率成分与工况1的区别,如图9所示。相对工况1来说,随着脉动压力分量增加的同时,各工况振动高频分量增加,低频段的振动反而有所降低,可进一步确认脉动压力分量主要影响管路高频段振动。
|
图 9 不同工况L2处频谱与工况1对比 Fig. 9 Comparison of L2 position spectrum under different working conditions and working condition 1 |
1) 压力脉动会在弯管处产生交变的激振力,脉动压力分量与静压力分量相比小时,对管路振动的影响甚微。当压力脉动逐渐增大时,弯管成为管路系统的振源,当脉动压力分量的数量级超过1%静压力时,弯管处的振源作用已经比较明显,靠近弯管处的振动比其他位置更为剧烈。
2) 在简单管路系统中,当压力脉动增大时,管路振动加速度级和压力脉动之间存在近于线性的增长关系。脉动压力分量对管路振动的影响主要体现在增加振动的高频分量,对复杂管路系统来说,压力脉动对管路振动的影响还要具体分析。
| [1] |
VETTER, GERHARD, FRIEDRICH S. Pressure pulsations in the piping of reciprocating pumps[J]. Chemical engineering & technology 10, 1987 (1): 262–271.
|
| [2] |
王秋颖. 输液管道压力脉动分析[J]. 装备制造技术, 2007(8): 48-49+53. WANG Q Y. Pressure pulsating analys is of pipeline[J]. Equipment Manufactring Technology, 2007(8): 48-49+53. |
| [3] |
周红, 刘永寿, 岳珠峰. 输流管道压力脉动计算分析[J]. 机械科学与技术, 2011(9): 1435-1438. ZHOU H, LIU Y S, YUE Z F. Calculation analyze of pressure pulsation in fluid flowing pipeline[J]. Mechanical Science and Technology for Aerospace Engineering, 2011(9): 1435-1438. |
| [4] |
LIANG Z, GUO C, WANG C. The Connection between flow pattern evolution and vibration in 90-degree pipeline: Bidirectional fluid‐structure interaction[J]. Energy Science & Engineering, 2022, 10(2): 308-323. |
| [5] |
YUAN W, DENG G, YANG Z. Experimental study and numerical analysis of fluid-structure coupling vibration characteristics for the reciprocating compressor pipeline[C]// IOP Conference Series: Earth and Environmental Science, IOP Publishing, 2020, 558(2): 022007.
|
| [6] |
朱丽, 白雪. 管路结构固液耦合振动有限元仿真分析技术[J]. 中国科技信息, 2017(21): 47-49. ZHOU L, BAI X. Finite element simulation analysis technology of solid-liquid coupling vibration of pipeline structure[J]. China Science and Technology Information, 2017(21): 47-49. |
| [7] |
熊雄, 周知进, 朱目成, 等. 压力脉动作用下管道的流固耦合瞬态分析[J]. 机床与液压, 2019, 47(16): 118-122. XIONG X, ZHOU Z J, ZHU M C, et al. Transient analysis of fluid-structure interaction of pipelines under pressure plusation[J]. Machine Tool & Hydraulics, 2019, 47(16): 118-122. |
| [8] |
窦益华, 于凯强, 杨向同, 等. 输流弯管流固耦合振动有限元分析[J]. 机械设计与制造工程, 2017, 46(2): 18-21. DOU Y H, YU K Q, YANG X T, et al. Finite element analysis of fluid structure coupling vibration of flow conveying bend[J]. Machine Design and Manufacturing Engineering, 2017, 46(2): 18-21. |
 2023, Vol. 45
2023, Vol. 45
