结构与材料的大变形问题模拟与仿真具有实际意义,在许多技术和工程领域具有重要意义。如在造船和海洋工程中,典型的大变形问题包括船体过载和船体与浮冰之间的相互作用[1],以及材料成型和制造工程。
为了解决大变形问题,在过去几十年中提出了各种数值方法。有网格方法例如任意拉格朗日-欧拉理论[2],无网格方法例如颗粒有限元法[3]、物质点法[4]、光滑粒子流体动力学[5]以及近场动力学方法[6]。
近场动力学(Peridynamics,PD)作为经典连续介质力学(Classical Continuum Mechanics,CCM)的重构,引入了独特的非局部框架,与分子动力学类似,考虑了成对粒子之间的非局部相互作用力,并建立了近场动力学的拉格朗日框架。在近场动力学中,任何一对粒子都存在一个力密度函数,并且假设粒子可在一个有限的范围内相互作用,该范围称为近场(horizon)。材料点处的应变能密度由其相邻材料点的变形确定。与CCM不同,PD框架中不需要连续场。因此,PD在处理不连续问题(如裂纹和损伤)方面具有优势[7-17]。
近场动力学根据键力的不同分为键基近场动力学和态基近场动力学,态基近场动力学又可分为常规态基近场动力学和非常规态基近场动力学。键基近场动力学模型普遍存在泊松比的限制,态基近场动力学通过构造非局部变形梯度建立与经典连续介质力学的联系,但变形梯度会存在奇异解。为此,本文从分子动力学角度从发,构造物质点间新型的微势函数,推导全新的本构模型,对研究近场动力学的适用性具有重要意义。
1 微势近场动力学模型为了避免现有键基近场动力学和非常规态基近场动力学存在的问题,并丰富现有常规态基近场动力学键力模型,在Fan等[18]工作基础上,进一步探究微势近场动力学模型(Micro-Potential Based Peridynamics,MPPD)的适用性。
1.1 本构模型推导 1.1.1 微观势能函数对于冰、岩石、陶瓷和混凝土等岩土材料,破坏过程受粘性断裂定律控制。为了模拟粘性变形,采用指数-指数微势函数:
| $ w\left( {{\Delta _{{n}}},{\Delta _{{t}}}} \right) = \phi - \phi \left( {1 + \frac{{{\Delta _{{n}}}}}{{{\delta _{{n}}}}}} \right)\exp \left( { - \frac{{{\Delta _{{n}}}}}{{{\delta _{{n}}}}} - \frac{{\Delta _{{t}}^2}}{{\delta _{{t}}^2}}} \right)。$ | (1) |
式中:
在MPPD模型中引入键长的二阶变形:
| $ \Delta {\text{ = }}{\left| {{{\boldsymbol{Y}}}\left\langle {\xi } \right\rangle } \right|^2} - {\left| {\xi } \right|^2}。$ | (2) |
式中:
| $ {{\boldsymbol{Y}}}\left\langle {\xi } \right\rangle = {{\boldsymbol{F}}\xi } 。$ | (3) |
式中,
用式(3)代替式(2)中的变形状态,得到:
| $ \Delta = 2{\xi ^{\text{T}}}{\boldsymbol{E}}\xi 。$ | (4) |
式中,
在MPPD模型中,提出了一种广义的非局部应变张量
| $ {{\boldsymbol{E}}}(x,t) = \frac{1}{4}\int_\mathcal{H} \omega \langle {\xi }\rangle \left( {\frac{{{{\boldsymbol{Y}}}\langle {\xi }\rangle {{\boldsymbol{Y}}}\langle {\xi }\rangle }}{{{{\xi }^{\text{T}}}{\xi }}} - 1} \right)\left( {5\frac{{{\xi } \otimes {\xi }}}{{{{\xi }^{\text{T}}}{\xi }}} - 1} \right){\rm{d}}{V_{\mathbf{\xi }}}。$ | (5) |
式中,影响函数
结合CCM理论,非局部偏应变可表述为:
| $ {{\boldsymbol{E}}'} = {{\boldsymbol{E}}} - \frac{{{E_{kk}}}}{3}{{\boldsymbol{I}}} 。$ | (6) |
式中,
| $ {E_{kk}} = \frac{1}{2}\int_H \omega \langle {\xi }\rangle \left( {\frac{{{{\boldsymbol{Y}}}\langle {\xi }\rangle {{\boldsymbol{Y}}}\langle {\xi }\rangle }}{{{{\xi }^{\text{T}}}{\xi }}} - 1} \right){\rm{d}}{V_{\mathbf{\xi }}} 。$ | (7) |
把式(6)和式(7)代入式(4)可得:
| $ \Delta = \frac{2}{3}{E_{kk}}{{\xi }^{\text{T}}}{\xi } + 2{{\xi }^{\text{T}}}{{\boldsymbol{E}}'\xi } 。$ | (8) |
式(8)右边第一项可看作由于体应变导致的键的变形,记为键长变化的法向分量:
| $ {\Delta _n} = \frac{2}{3}{E_{kk}}{{\xi }^{\text{T}}}{\xi } 。$ | (9) |
第二项可看作由于偏应变导致的键的变形,记为键长变化的切向分量:
| $ {\Delta _t} = 2{{\xi }^{\text{T}}}{{\boldsymbol{E}}'\xi }。$ | (10) |
键基近场动力学中当键长发生变化时,微势能被储存在键中,从而导致单个粒子的宏观非局部弹性应变能密度(Nonlocal Elastic Strain Energy Density,NESED),定义为:
| $ W = \frac{1}{2}\int_\mathcal{H} w (\eta ,\xi ){\rm{d}}{V_\xi }。$ | (11) |
为了得到MPPD的本构模型,首先取式(11)的变分:
| $ \delta {W^{non}} = \int_\mathcal{H} \delta w{\rm{d}}{V_\xi } = \frac{1}{2}\int_\mathcal{H} {\left( {{F_n}\delta {\Delta _n} + {F_t}\delta {\Delta _t}} \right)} {\rm{d}}{V_\xi } 。$ | (12) |
式中:
将式(9)和式(10)代入式(12),经过计算可得:
| $ \delta {W^{{\text{non}}}} = \frac{1}{2}\int_\mathcal{H} {\left[ {\frac{2}{3}\left( {{F_n} - {F_t}} \right)|\xi {|^2}\delta {E_{kk}} + 2{F_t}{\xi ^{\text{T}}}\delta {{\boldsymbol{E}}}\xi } \right]} {\rm{d}}{V_\xi }。$ | (13) |
可以发现:
| $ {\xi ^{\text{T}}}\delta {{\boldsymbol{E}}}\xi = \frac{1}{2}\delta \Delta = \frac{1}{2}\delta \left( {|{Y}\langle \xi \rangle {|^2} - {\xi ^2}} \right) = {{\boldsymbol{Y}}}\langle \xi \rangle \cdot \delta {{\boldsymbol{Y}}}\langle \xi \rangle。$ | (14) |
其中:
| $ \delta {{\boldsymbol{E}}} = \frac{1}{2}\int_\mathcal{H} \omega \langle {\xi }\rangle \frac{{{{\boldsymbol{Y}}}\langle {\xi }\rangle \delta {{\boldsymbol{Y}}}\langle {\xi }\rangle }}{{{{\xi }^{\text{T}}}{\xi }}}\left( {5\frac{{{\xi } \otimes {\xi }}}{{{{\xi }^{\text{T}}}{\xi }}} - 1} \right){\rm{d}}{V_{\xi }} ,$ | (15) |
| $ \delta {E_{kk}} = \frac{1}{2}\int_H \omega \langle {\xi }\rangle \frac{{{{\boldsymbol{Y}}}\langle {\mathbf{\xi }}\rangle \delta {{\boldsymbol{Y}}}\langle {\xi }\rangle }}{{{{\xi }^{\text{T}}}{\xi }}}{\rm{d}}{V_{\xi }} 。$ | (16) |
把式(15)和式(16)代入式(13),可得:
| $ \begin{split} \delta {W^{{\text{non}}}} =& \frac{1}{3}\int_\mathcal{H} {\left( {{F_n} - {F_t}} \right)} {\xi ^2}{\rm{d}}{V_\xi }\int_\mathcal{H} \omega \langle \beta \rangle \frac{{{{\boldsymbol{Y}}}\langle \beta \rangle \cdot \delta {{\boldsymbol{Y}}}\langle \beta \rangle }}{{{\beta ^{\text{T}}}\beta }}{\rm{d}}{V_\beta }+ \\ & \int_\mathcal{H} {{F_t}} {{\boldsymbol{Y}}}\langle \xi \rangle \cdot \delta {{\boldsymbol{Y}}}\langle \xi \rangle {\rm{d}}{V_\xi }。\\[-10pt] \end{split} $ | (17) |
式中,使用
| $ {A} \cdot {{\boldsymbol{B}}}: = \int_\mathcal{H} {({{\boldsymbol{AB}}})} \langle \xi \rangle {\rm{d}}{V_\xi }。$ | (18) |
通过非局部弹性应变能密度的导数可得到本构关系,第一项进行积分变换
| $ \begin{split} \delta {W^{{\text{non }}}} = & \int_\mathcal{H} {\left[ {\frac{1}{3}\omega \langle \xi \rangle {\xi ^{ - 2}}\int_\mathcal{H} {\left( {{F_n} - {F_t}} \right)} {\beta ^2}d{V_\beta } + {F_t}} \right]}\;\times\\ & {{\boldsymbol{Y}}}\langle \xi \rangle \delta {{\boldsymbol{Y}}}\langle \xi \rangle {\rm{d}}{V_\xi }。\end{split} $ | (19) |
根据式(19),可得本构关系:
| $ {{\boldsymbol{T}}}\langle \xi \rangle = \left[ {\frac{1}{3}\omega (\xi ){\xi ^{ - 2}}\int_\mathcal{H} {\left( {{F_n} - {F_t}} \right)} {\beta ^2}{\rm{d}}{V_\beta } + {F_t}(\xi )} \right]{{\boldsymbol{Y}}}\langle \xi \rangle 。$ | (20) |
式中,力态可分解为
| $ {{\boldsymbol{T}}}\langle \xi \rangle = {{{\boldsymbol{T}}}_1}\langle \xi \rangle + {{{\boldsymbol{T}}}_2}\langle \xi \rangle。$ | (21) |
式中:
幂指数型微势的应用很难得到描述键合力密度的具体表达式。为使问题具体化,在MPPD模型中,通过分析各向同性均匀变形的平面应力场来标定键参数。本构方程
假设材料经历一个各向同性的弹性无穷小变形,这时非局部弹性应变能密度与在经典的连续介质力学框架下各向同性下的线弹性应变能密度相等,可得:
| $ \frac{\phi }{{\delta _n^2}} = \frac{{21}}{{16{\text{π}}{\delta ^7}}}(3\lambda + 2\mu ) = \frac{{63}}{{16{\text{π}} {\delta ^7}}}K 。$ | (22) |
式中,K为体积模量,
同样,假设材料不发生任何体积变化。可得如下关系:
| $ \frac{{\delta _n^2}}{{\delta _t^2}} = \frac{{5(1 - 2\nu )}}{{2(1 + \nu )}} 。$ | (23) |
物体
对于二维问题,断裂穿过单位裂纹面所有键所需的能量如下:
| $ {G_{{\text{II}}0}} = \int_0^\delta {\int_0^t {\int_z^\delta {\int_0^{{{\cos }^{ - 1}}z/\xi } {{w_c}\xi \sin \theta } } } } {\text{d}}\theta {\text{d}}\xi {\text{d}}x{\text{d}}z。$ | (24) |
式中,
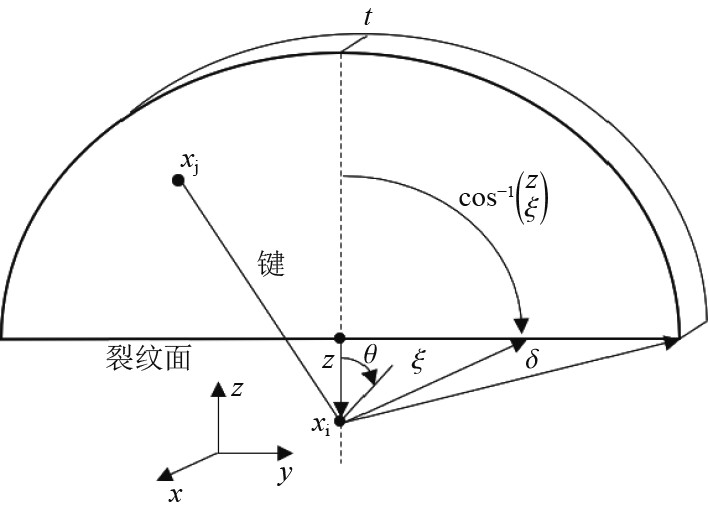
|
图 1 断裂面示意图 Fig. 1 Schematic illustration for fracture surface |
计算式(24),得到能量释放率为:
| $ {G_{{\text{II}}0}} = \frac{{2{\delta ^3}t{w_c}}}{3} 。$ | (25) |
由于能量释放率可通过脆性材料的试验测试获得,求解式(25)得到二维问题中键失效的临界能为:
| $ {w_c} = \frac{{3{G_{{\text{II}}0}}}}{{2{\delta ^3}t}}。$ | (26) |
在当前的断裂准则中,当总微势能
| $ \mu \left(x,{x}^{\prime },t\right)=\left\{\begin{array}{ll}1,& w\left(x,{x}^{\prime },{\text{Y}}_{n}\right) < {w}_{c},\\ 0,\text{}\text{} & \text{ }{\rm{others}}\text{ }。\end{array} \right.$ | (27) |
基于近场动力学公式,Silling等开发了近场动力学计算框架,可用于研究材料和结构的变形和断裂行为,如EMU、peridigm[19-21]。简要介绍近场动力学的数值实现技术。由于近场动力学的运动方程是积分-微分形式,理论求解难度很大。因此,基于空间离散格式的数值技术用于计算积分方程。在现有的近场动力学模型中,多是考虑到无网格方法空间离散的简单性而被采用。在该框架下,首先将连续体离散成一系列具有一定体积形状的物质点,然后对离散的物质点进行空间积分得到其相应的物理量。
2.1 运动方程离散作为无网格方法的优点之一,在预处理阶段,即空间离散时不需要网格化。作为一种非局部理论,其本构模型自然包含了损伤和断裂的描述,从而避开了传统有限元失效分析中的不连续性和网格重构。在计算中,近场动力学运动方程离散为每个物质点的一系列离散运动方程:
| $ {\rho _i}{\ddot u}\left[ {{x_i},{t_n}} \right] = \sum\limits_{j = 1}^N {\left( {{{\boldsymbol{T}}}\left[ {{x_i},{t_n}} \right]\left\langle {{\xi _{ij}}} \right\rangle - {{\boldsymbol{T}}}\left[ {{x_j},{t_n}} \right]\left\langle {{\xi _{ji}}} \right\rangle } \right)} \Delta {V_{{x_j}}} + {{\boldsymbol{b}}}\left[ {{x_i},{t_n}} \right]。$ | (28) |
式中:下标i, j分别为粒子标号;N为物质点近场内粒子总数;
MPPD的非局部体积应变计算:
| $ {{\boldsymbol{E}}}\left[ {{x_i},{t_n}} \right] = \frac{1}{4}\sum\limits_{j = 1}^N \omega \langle {\xi }\rangle \left( {\frac{{{{\boldsymbol{Y}}}\langle {\mathbf{\xi }}\rangle {{\boldsymbol{Y}}}\langle {\xi }\rangle }}{{{{\xi }^{\text{T}}}{\xi }}} - 1} \right)\left( {5\frac{{{\xi } \otimes {\xi }}}{{{{\xi }^{\text{T}}}{\xi }}} - 1} \right)\Delta {V_{{x_j}}}。$ | (29) |
利用速度Verlet算法对粒子的速度和位移进行更新:
| $ \left\{ {\begin{array}{*{20}{l}} {{\dot u}[{x_i},{t_{n + \frac{1}{2}}}] = {u}[{x_i},{t_n}] + {\ddot u}[{x_i},{t_n}] \cdot \dfrac{{\Delta t}}{2}},\\ {{u}[{x_i},{t_{n + 1}}] = {u}[{x_i},{t_n}] + {\dot u}[{x_i},{t_{n + \frac{1}{2}}}] \cdot \Delta t} ,\\ {{\dot u}[{x_i},{t_{n + 1}}] = {\dot u}[{x_i},{t_{n + \frac{1}{2}}}] + {\ddot u}[{x_i},{t_{n + 1}}] \cdot \dfrac{{\Delta t}}{2}} 。\end{array}} \right. $ | (30) |
式中,∆t为计算时间步长。
显式格式求解的一个主要局限性是条件稳定,这意味着最大容许时间增量必须小于波传播到最小单元长度所需的时间,所用时间称为稳定时间增量。根据Von Neumann稳定性分析的经典假设,式(28)中使用的时间增量的稳定性条件如下:
| $ \Delta t < \sqrt {\frac{{2\rho }}{{\sum\limits_{{x_j} \in {{H}}x} {{V_j}} c\left( {{x_j} - {x_i}} \right)}}} 。$ | (31) |
近场动力学在数值实现中将连续体离散为一定数量具有一定体积形状的物质点,这将导致位于近场范围边界处的物质点体积计算不准确。
由近场动力学理论的非局部特性可知,物质点

|
图 2 体积修正 Fig. 2 The volume correction |
为了解决处于近场范围边界处物质点体积计算不准确的问题,一个可行的方法是对处于近场范围边界处的物质点在计算体积时进行特殊处理,即对物质点在计算体积时乘以相应的体积修正系数,称之为体积修正。本文采用的体积修正方案为:
| $ {\alpha }_{{x}_{j}}(\xi )=\left\{\begin{split}&1,\text{if}\; \xi ⩽(\delta -0.5\Delta x),\\& \dfrac{\delta -\xi +0.5\Delta x}{\Delta x},\text{if}\;(\delta -0.5\Delta x) < \xi ⩽\delta ,\\ &0,{\rm{others}}。\end{split}\right. $ | (32) |
考虑体积修正,运动方程(28)写为:
| $ \begin{split} {\rho _i}{\ddot u}\left[ {{x_i},{t_n}} \right] = & \sum\limits_{j = 1}^N {\left( {{{\boldsymbol{T}}}\left[ {{x_i},{t_n}} \right]\left\langle {{\xi _{ij}}} \right\rangle - {{\boldsymbol{T}}}\left[ {{x_j},{t_n}} \right]\left\langle {{\xi _{ji}}} \right\rangle } \right)} ,\\ & ({\alpha _{{x_j}}}\Delta {V_{{x_j}}}) + {{\boldsymbol{b}}}\left[ {{x_i},{t_n}} \right]。\end{split} $ | (33) |
采用具有中心孔的矩形板两端受均布载荷来验证当前近场动力学模型,并与Le等[22]结果对比,如图3所示。矩形板的上下边界采用自由边界,模型的左右两边界分别承受1MPa的均布拉伸载荷作用。模型的尺寸为100 mm×50 mm×10 mm,孔的半径为10 mm。材料属性为:弹性模量为100 GPa,泊松比为0.4,材料密度为2000 kg/m3。

|
图 3 开孔平板受拉伸载荷作用示意图 Fig. 3 The illustration of a plate with a hole subjected to tensile loads |
在计算中模型离散粒子尺寸dx=0.025 cm,近场半径
将提出的模型得到的位移场与现有的常规态基近场动力学模型得到的水平和垂直位移场进行比较,验证当前模型计算的准确性。从图4可看出,本文改进的近场动力学得到的数值结果与常规态基近场动力学模型得到的收敛结果一致。同时也可发现当前模型的收敛速度较Le等[22]常规态基近场动力学模型慢。这是因为当前模型在计算键力时一方面需多次计算粒子近场的积分解;另一方面本文采用较复杂的复合幂型指数函数,这些都增加了计算量。通过比较最终收敛后的结果,可验证本文模型的正确性和准确性。

|
图 4 模拟位移分布对比,左边本文模型结果,右边Le等[22]的结果 Fig. 4 The displacement in horizon,left is current results and right is Le's[22] results |
图5和图6给出了A和B 2个点位移和速度的定量对比结果,其中黑色方块代表本文模型计算数据,黑色三角形代表Le等[22]的计算结果。
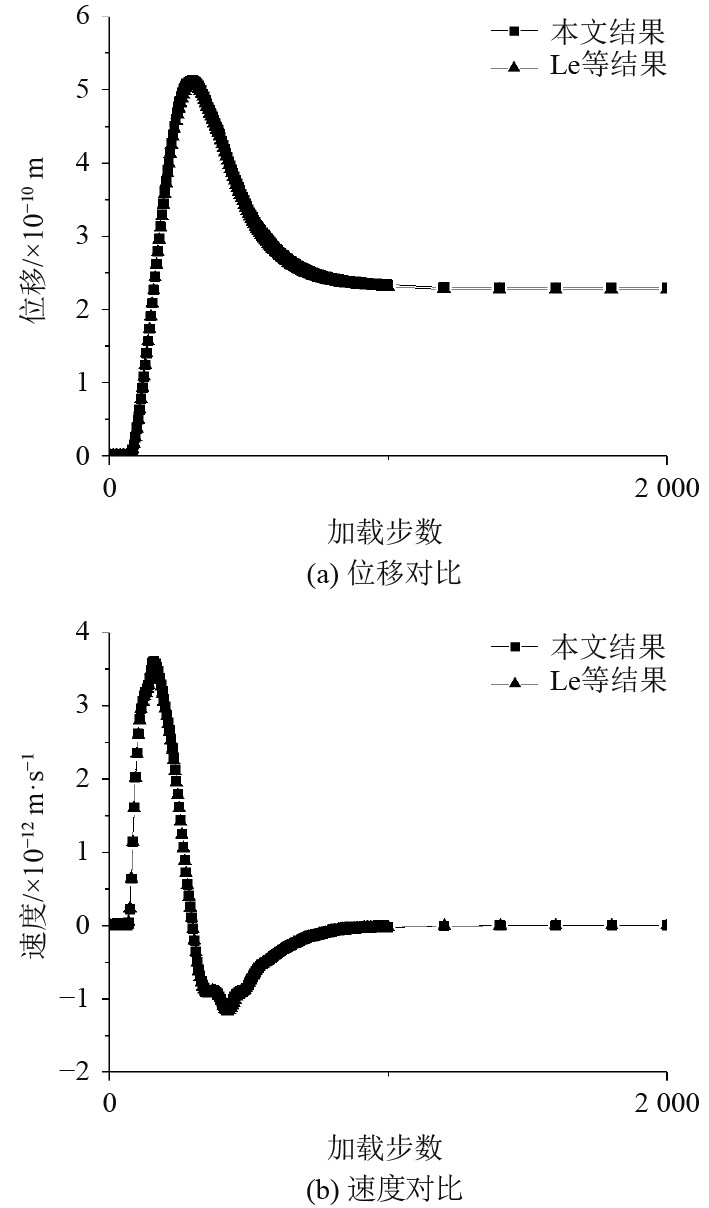
|
图 5 A点位移与速度结果对比 Fig. 5 The displacement and velocity of point A |

|
图 6 B点位移与速度结果对比 Fig. 6 The displacement and velocity of point B |
由图5和图6可以发现,垂直和水平位移在大约1 000次迭代时达到稳态值,表明了本文模型准静态动力学问题的模拟是有效的。
3.2 有限变形算例MPPD模拟的有限变形采用悬臂梁一侧受集中力另一侧固定来研究。悬臂梁的几何尺寸如图7所示。MPPD模型采用自适应动态松弛方法,有效解决准静态问题模拟。选取3个沿悬臂梁上侧面长度方向均匀分布的粒子P1、P2、P3,研究其位移。力学参数为:弹性模量100.0 MPa,泊松比0.3,材料密度7800 kg/m3。长度L=10.0 m,高度H=1.0 m,集中力P=1 MPa。
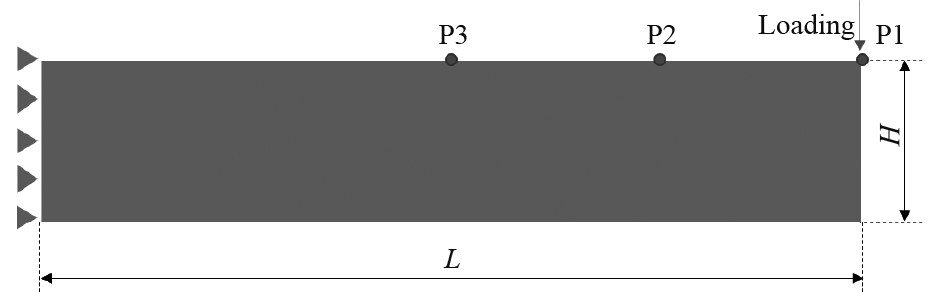
|
图 7 受集中力作用悬臂梁示意图 Fig. 7 Schematic illustration for cantilever under concentrated load |
图8给出了采用当前MPPD模型模拟悬臂梁变形过程的垂直和水平方向云图。由图8可以发现,当前MPPD模型能够比较稳定地模拟有限变形过程。
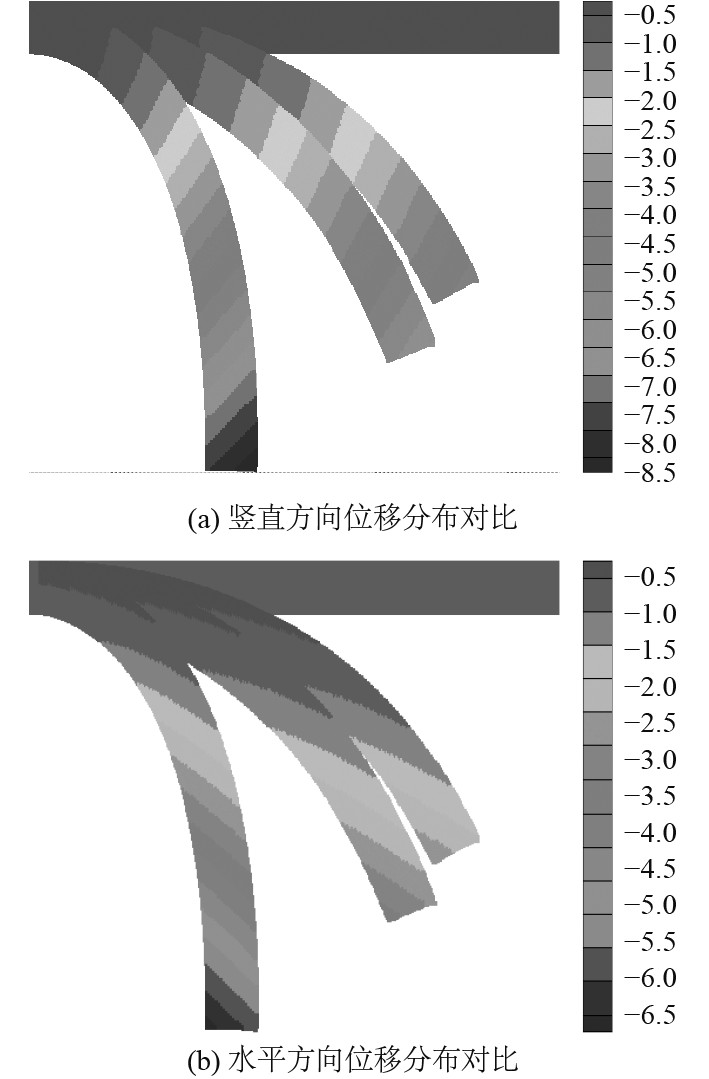
|
图 8 受集中力作用悬臂梁位移云图 Fig. 8 Displacement contour for cantilever under concentrated load |
图9给出了采用MPPD,有限元和Le等模型计算的5个标记点在竖直方向和水平方向的位移对比结果。由图9可以发现,当前MPPD模型在垂直和水平位移均与有限元结果较为吻合,从而说明当前MPPD模型能够有效模拟有限变形问题。
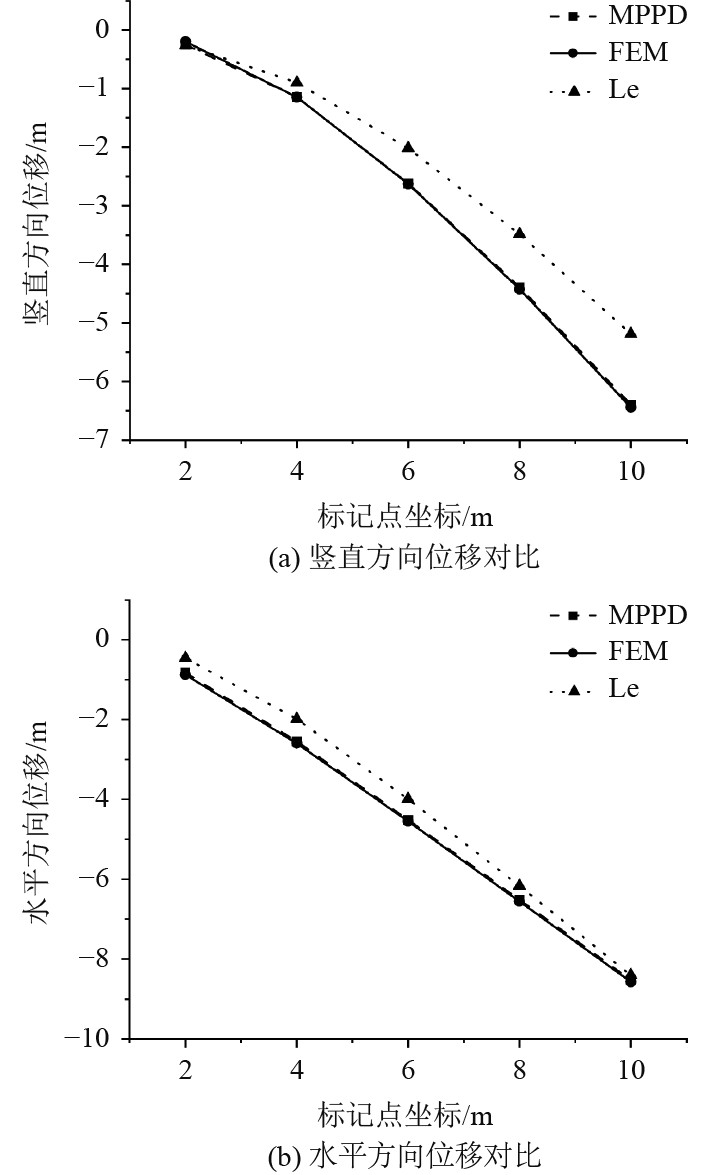
|
图 9 受集中力作用悬臂梁位移对比 Fig. 9 Dsiplacement for cantilever under concentrated load |
本文推导了采用微势能的近场动力学本构模型,标定了平面应力问题的键参数,给出了数值实现的离散格式,并考虑了采用粒子离散时的数值修正因素,最后分析了无限变形和有限变形问题。结论如下:
1)采用二阶变形作为键长变形的度量,结合指数-指数微势函数推导的微势近场动力学模型能够有效模拟材料变形问题。
2)MPPD模型可以同时模拟无限变形和有限变形,与现有常规态基近场动力学模型相比,MPPD模型能够获得较为准确的结果。
| [1] |
王林, 夏峰. 浮冰与极地船舶抗冰结构碰撞研究[J]. 舰船科学技术, 2022(15): 44. WANG Lin, XIA Feng. Research on collision between ice floe and polar ship ice-resistant structure[J]. Ship Science and Technology, 2022(15): 44. |
| [2] |
WANG D, BIENEN B, NAZEM M, et al. Large deformation finite element analyses in geotechnical engineering[J]. Computers & Geotechnics, 2015, 65: 104-114. |
| [3] |
YUAN W, WANG H, ZHANG W, et al. Particle finite element method implementation for large deformation analysis using Abaqus[J]. Acta Geotechnica, 2021(12): 1-14. |
| [4] |
DONG Y. Reseeding of particles in the material point method for soil–structure interactions[J]. Computers and Geotechnics, 2020, 127(1): 103-716. |
| [5] |
PENG C, BAUINGER C, SZEWC K, et al. An improved predictive-corrective incompressible smoothed particle hydrodynamics method for fluid flow modelling[J]. Journal of Hydrodynamics, 2019, 31(S1): 1-15. |
| [6] |
SILLING S. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175-209. DOI:10.1016/S0022-5096(99)00029-0 |
| [7] |
朱其志, 李惟简, 尤涛, 等. 扩展键基近场动力学的几何非线性扩展[J]. 同济大学学报: 自然科学版, 2022, 50(4): 8.
|
| [8] |
张建宇, 韩非, 江柏红, 等 基于显微CT图像的近场动力学建模与复合材料微结构破坏模拟[J]. 固体力学学报, 2022, 43(2): 15.
|
| [9] |
张恒, 张雄, 乔丕忠. 近场动力学在断裂力学领域的研究进展[J]. 力学进展, 2022, 52: 1−22. ZHANG Heng, ZHANG Xiong, QIAO Pizhong. Advances of peridynamics in fracture mechanics[J]. Advances in Mechanics, 2022, 52: 1−22. |
| [10] |
王庆, 李家宝, 鞠磊, 等. 一维无源对流扩散方程的近场动力学计算格式[J]. 哈尔滨工程大学学报, 2022, 43(1): 9-16. WANG Qing, LI Jiabao, JU Lei, et al. Peridynamic calculation scheme of a one-dimensional passive convection-diffusion equation[J]. Journal of Harbin Engineering University, 2022, 43(1): 9-16. DOI:10.11990/jheu.202010006 |
| [11] |
薛彦卓, 刘仁伟, 王庆, 等 近场动力学在冰区船舶与海洋结构物中的应用进展与展望[J]. 中国舰船研究, 2021, 16(5): 16. XUE Yanzhuo, LIU Renwei, WANG Qing, et al. Advances in application of peridynamics for ships and marine structures in ice zones[J]. Chinese Journal of Ship Research, 2021, 16(5): 1–15, 63. |
| [12] |
王超, 曹成杰, 熊伟鹏, 等. 基于近场动力学的破冰阻力预报方法研究[J]. 哈尔滨工程大学学报, 2021, 42(1): 1-7. WANG Chao, CAO Chengjie, XIONG Weipeng, et al. Prediction method of ice-breaking resistance based on peridynamics theory[J]. Journal of Harbin Engineering University, 2021, 42(1): 1-7. |
| [13] |
马鹏飞, 李树忱, 袁超, 等. 基于SED准则的近场动力学及岩石类材料裂纹扩展模拟[J]. 岩土工程学报, 2021, 43(6): 9.
|
| [14] |
周小平, 王允腾, 钱七虎. 爆破荷载作用下岩石破坏特性的"共轭键"基近场动力学数值模拟研究[J]. 中国科学:物理学、力学、天文学, 2020, 50(2): 13. |
| [15] |
杨娜娜, 赵天佑, 陈志鹏, 等. 破片冲击作用下舰船复合材料结构损伤的近场动力学模拟[J]. 爆炸与冲击, 2020, 40(2): 11. YANG Nana, ZHAO Tianyou, CHEN Zhipeng, et al. Peridynamic simulation of damage of ship composite structure underfragments impact[J]. Explosion and Shock Waves, 2020, 40(2): 11. DOI:10.11883/bzycj-2019-0019 |
| [16] |
熊伟鹏, 王超, 傅江妍, 等. 冰球冲击试验的近场动力学方法数值模拟[J]. 振动与冲击, 2020, 39(7): 8. XIONG Weipeng, WANG Chao, FU Jiangyan, et al. Numerical simulation of ice sphere impact test by peridynamics method[J]. Journal of Vibration and Shock, 2020, 39(7): 8. |
| [17] |
黄丹, 章青, 乔丕忠等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4). HUANG Dan, ZHANG Qing, QIAO Pizhong, et al. A review on peridynamics method and its applications[J]. Advances in Mechanics, 2010, 40(4). |
| [18] |
FAN J, LIU R, LI S, et al. A micro-potential based Peridynamic method for deformation and fracturing in solids: A two-dimensional formulation[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 360. DOI:10.1016/j.cma.2019.112751 |
| [19] |
LITTLEWOOD D. Roadmap for peridynamic software implementation[R]. 2015.
|
| [20] |
PARKS M, LEHOUCQ R, PLIMPTON S, et al. Implementing peridynamics within a molecular dynamics code[J]. Computer Physics Comnunications, 2007, 179(11): 777−783.
|
| [21] |
SILLING S, ASKARI E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computes and Structures, 2005, 83(17−18): 1526−1535.
|
| [22] |
LE Q, CHAN W, SCHWARTZ J. A two-dimensional ordinary, state-based peridynamic model for linearly elastic solids[J]. International Journal for Numerical Methods in Engineering, 2014, 98(8): 547−561.
|
 2023, Vol. 45
2023, Vol. 45
