Simplified tension calculation of mooring line for storm mooring systems
0 引 言 防风系泊(水鼓)系统是一种在近岸浅水区域的单点系泊系统,其系泊线结构通常由多段不同的系泊链、缆组成,并配有重砣、浮筒(水鼓)等[1],是组合(多成分)系泊线结构[2]。目前,组合系泊线结构较多采用基于分段外推法等的计算方法[3-4],主要应用于较长的深水系泊系统系泊线[5]和相对松弛的状态[6],同时需要使用数值迭代等计算方法,过程较为繁琐。而防风系泊系统系泊线较短且承载时通常表现为张紧状态,与传统意义上的系泊线结构有所不同。因此在悬链线理论基础上,针对防风系泊系统系泊线的特点,采用“以直代曲”的几何近似条件,对系泊线张力进行简化计算,便于在初步设计阶段能够快速简便地进行应用分析。
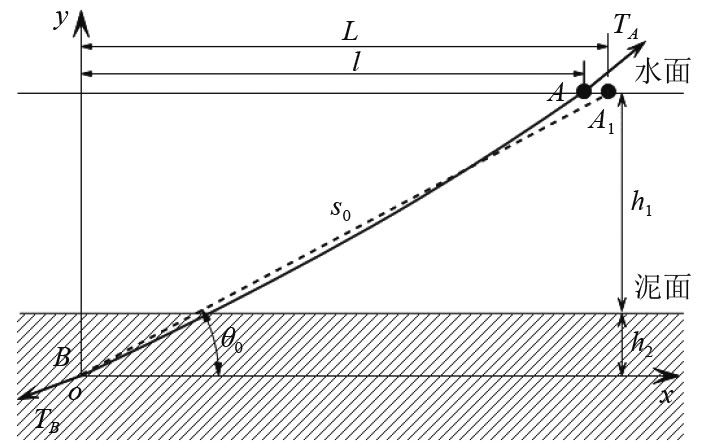
1 简化计算方法 1.1 使用简化计算的条件 以链长为s0(m),水下单位长度重量为w(kN/m)的系泊链的锚点B点为原点,建立如图1所示的坐标系,水深为h1(m),锚点处的埋深为h2(m),B点到水面的距离为z(m),
$z = {h_1} + {h_2}$
。假定系泊链在系泊力
${T_{{H}}}$
(
${\text{kN}}$
)作用下,正好位于自由链的临界状态的A0点,即系泊链底端B点处正好与水平方向一致,此时水平距离为
${l_0}$
。随着系泊力增大,A点继续向右移动,系泊链变为约束链[6]状态。A1点为理论极限状态(直线状态),此时极限水平距离为
$L$
(
${\text{m}}$
),
$L = \sqrt {s_0^2 - {z^2}} $
。根据文献[7-8]中的分析,A点在靠近A1的过程中,系泊力呈现指数型增长的趋势并趋于无穷大。悬链线理论计算公式
${s_0} = \sqrt {2{c_0}z + {z^2}} $
,
$ s = c \cdot \sinh \Bigg(\dfrac{x}{c}\Bigg)$
和
${L^2} + {z^2} = s_0^2$
,其中c为悬链线参数(
${\text{m}}$
),
$c = \dfrac{{{T_{{H}}}}}{w}$
,则A0点处悬链线参数
${c_0}\left( {\text{m}} \right)$
和临界水平距离
${l_0}\left( {\text{m}} \right)$
的关系如下式:
|
$\left\{\begin{aligned} & {{c_0} = \dfrac{{{L^2}}}{{2z}}} ,\\ & {{l_0} = \dfrac{{{L^2}}}{{2z}} \cdot {\text{arcsinh}}\Bigg(\dfrac{{2z{s_0}}}{{{L^2}}}\Bigg)} 。\end{aligned}\right.$
|
(1) |
根据文献[7-8]中广义倾角
$\beta $
满足的条件
$\beta = \dfrac{l}{{2c}} = \dfrac{{l \cdot {T_{{H}}}}}{{2w}}$
和
$ \sinh \left( \beta \right) = \dfrac{L}{{2c}} $
,代入悬链线参数
$c$
,可推导得到A点水平距离与张力满足的关系:
|
$ l = 2c \cdot {\text{arcsinh}}\left( {\dfrac{L}{{2c}}} \right) = \dfrac{{2{T_{{H}}}}}{w} \cdot {\text{arcsinh}}\left( {\dfrac{{wL}}{{2{T_{{H}}}}}} \right)。$
|
(2) |
式(2)表明系泊点A点位置即系泊线的水平位移
$l$
,受到几何条件(
${s_0}$
,
$z$
)、和受力条件(
${T_{{H}}}$
,
$w$
)的影响。令参数
$t = \dfrac{L}{{2c}} = \dfrac{{w \cdot L}}{{2 \cdot {T_{{H}}}}}$
,构造无量纲函数
${L} \left( t \right)$
如式(3),表示水平距离
$l$
接近极限距离
$L$
的程度。
|
$ {L} \left(t\right) = \dfrac{{L - l}}{L} = 1 - \dfrac{{{\text{arcsinh}}\left( t \right)}}{t} 。$
|
(3) |
对于给定链长
${s_0}$
的系泊线,
$L$
为定值,因此随着系泊力
${T_{{H}}}$
增大,悬链线参数
$c$
增大,
$t$
减小,
${L} \left( t \right)$
趋近于0。对于任意的单系泊线状态,满足参数
$t$
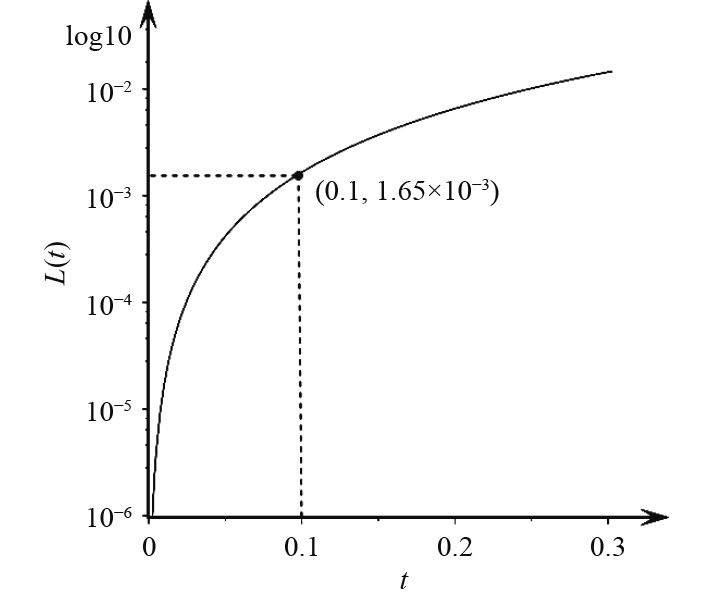
时,均有符合函数图像(见图2)的关系。当t=0.1时,
$L\left( {0.1} \right) \approx 1.65 \times {10^{ - 3}}$
,则有
$L - l < 0.165{\text{% }}L$
。防风系泊系统的系泊线长度通常不超过100 m,因此当
$t < 0.1$
,
$l$
与
$L$
的差值小于2 m,可近似认为系泊点在极限位置,即系泊链状态可近似为极限状态时的直线状态。由
$t$
的定义关系,得到
${T_{{H}}}$
或
$c$
满足式(4)的条件。大型舰船防风系泊时的系泊力一般都大于1000
${\text{kN}}$
[9],常用型号的系泊链在实际工况中较为容易满足。
|
$ {T}_{{H}} > 5wL或c > 5L 。$
|
(4) |
1.2 单系泊线的简化计算 建立坐标系如图3所示。其中曲线AB为系泊线实际状态,虚线A1B为极限状态时直线状态。对单系泊线整体进行受力分析得到:
|
$ \Bigg\{\begin{aligned}&竖直方向分力平衡:{T}_{{VA}}={T}_{{VB}}+{G}_{0},\\ &水平方向分力平衡:{T}_{{HA}}={T}_{{HB}}={T}_{{H}}。\end{aligned} $
|
(5) |
其中,
${G_0}$
(
${\text{kN}}$
)为系泊链的水下重量,
${G_0} = w \cdot {s_0}$
。
${T_{{H}}}$
(
${\rm{kN}} $
)为系泊舰船受到系泊力与系泊链受到水流作用力的合力。由于系泊点
A
与极限位置A1的距离较小,系泊链状态接近于直线状态,因此将曲线AB切向角
${\theta _B}$
近似于直线倾角
${\theta _0}$
,即
$\tan ({\theta _{{B}}}) = \dfrac{{{T_{{{VB}}}}}}{{{T_{{{HB}}}}}} \approx \tan \left( {{\theta _{{0}}}} \right) = \dfrac{z}{L}$
,得到B点的竖直方向分力为:
|
$ {T_{{{VB}}}} = \dfrac{z}{L} \cdot {T_{{H}}},$
|
(6) |
利用力的三角形法则得到B点的张力为:
|
$ {T_{{B}}} = \sqrt {T_{{H}}^2 + T_{{{VB}}}^2} = \dfrac{{{s_0}}}{L} \cdot {T_{{H}}} 7 ,$
|
联立式(5)、式(6)得到A点的竖直方向分力为:
|
$ {T_{{{VA}}}} = \dfrac{z}{L} \cdot {T_{{H}}} + w \cdot {s_0}。$
|
(7) |
根据悬链线理论,系泊线AB上A点处水平分力和竖直分力满足
$ \tan \left( {{\theta _{\text{A}}}} \right) = \dfrac{{{T_{{{VA}}}}}}{{{T_{{H}}}}} $
,得到A点的张力为:TA =
$ \sqrt {T_H^2 + T_{VA}^2} = \sqrt {T_0^2 + {{(\dfrac{z}{L}{T_H} + w \cdot {s_0})}^2}} = {T_0} \cdot \sqrt {{{\left( {\dfrac{s}{L}} \right)}^2} + 2 \cdot \dfrac{z}{L} \cdot \dfrac{{w \cdot {s_0}}}{{{T_H}}} + {{\left( {\dfrac{{w \cdot {s_0}}}{{{T_H}}}} \right)}^2}} 。$
设
$\dfrac{{w \cdot {s_0}}}{{{T_{{H}}}}} = x$
,将
${T_{{A}}}$
在
$x$
处Taylor展开,得到:
$ {T_{{A}}} = \dfrac{{{s_0}}}{L} \cdot {T_{{H}}} + \dfrac{z}{{{s_0}}} \cdot {T_{{H}}} \cdot x + \dfrac{1}{2} \cdot \dfrac{{{L^3}}}{{s_0^3}} \cdot {T_{{H}}} \cdot {x^2} + o\left( {{x^3}} \right) $
,略去2阶以上小量,得到A点张力:
|
$ {T_{{A}}} = \dfrac{{{s_0}}}{L} \cdot {T_{{H}}} + w \cdot z。$
|
(8) |
对于图3中在系泊线上距离B点链长为
$ {s_q} $
(
${s_{{q}}} \in \left[ {0,{s_0}} \right]$
)的任意一点
$ Q $
,结果如表1所示。
表 1(Tab. 1)

表 1 Q点的力和切角
Tab. 1 Force and tangent angle at point Q
| 参数 |
计算公式 |
| 竖向分力TVQ/kN
|
${T_{ {{VQ} } } } = \dfrac{z}{L} \cdot {T_{{H} } } + w \cdot {s_{{q} } }$
|
| 张力TQ/kN
|
${T_{{Q} } } = \dfrac{ { {s_0} } }{L} \cdot {T_{{H} } } + \dfrac{ {z \cdot w \cdot {s_{{q} } } }}{ { {s_0} } }$
|
| 切向角
${\theta _{\text{Q}}}$
/rad
|
${\theta _{{Q} } } = \arctan \left(\dfrac{z}{L} + \dfrac{ { {s_0} } }{c}\right)$
|
|
表 1 Q点的力和切角
Tab.1 Force and tangent angle at point Q
|
单系泊线的简化计算方法是将系泊线从几何上假设为直线进行推导求解力及其切向角,因此切向角
${\theta _{\text{Q}}}$
为张力与水平分力之间的夹角,与几何关系中的直线与水平方向的夹角
${\theta _0}$
不同。由几何关系可知B点处
$ {\theta _{{B}}} < {\theta _0} $
,结合表1中的公式,因此竖向分力和张力的计算值较悬链线理论的计算值偏大,计算偏于安全。由表1可知,系泊链的最大张力
${T_{\max }} = {T_{{A}}}$
,得到锚点B的受力
${T_{{B}}} = {T_{\max }} - w \cdot z$
。由于系泊线无卧底段,令CCS标准[10]中锚点的水平作用力
$P\left( {{\text{kN}}} \right)$
估算公式
$P = {T_{\max }} - w \cdot z - {F_f}$
中的海底摩檫力
${F_f} = 0$
,两者形式上完全一致,但CCS规范中的锚点张力
$P \cdot \sec {\theta _{{B}}} > $
${T_{\max }} - w \cdot z = {T_{{B}}}$
,更加保守。
1.3 组合系泊线的简化计算 如图4所示防风系泊系统系泊线可分为3段,由质量较重的底链
${s_1}$
、质量较轻的上端链
${s_2}$
、系泊缆
${s_3}$
、浮筒1和重块2组成。在悬链线理论的假设条件下,将浮筒和重块的作用力简化为在1点和2点的集中力
${P_1}\left( {{\text{kN}}} \right)$
和
${P_2}\left( {{\text{kN}}} \right)$
,并将舰船上的系泊点A点近似在水面位置。悬链线方法、近似抛物线方法求解张力时通常需要进行数值迭代的方法进行,计算较为复杂。
文献[6]中,认为组合系泊线中的每一段仍可以看作是对应不同参数
$c$
悬链线上的一部分,因此每一段均可以进行独立分析。根据悬链线理论,系泊线上任意一点所受到的水平分力均等于系泊点A处的系泊力
${T_{{H}}}$
,因此对于每一段线均有
${t_i} = \dfrac{{{L_i}}}{{2{c_i}}} = $
$ \dfrac{{{L_i}{w_i}}}{{2{T_H}}}\left( {i = 1,2,3} \right)$
,但由于每段系泊线的状态并未明确(
${L_i}$
无法求解),因此无法对
${t_i}$
进行判断。对各段的
${t_i}$
求和得到
$ \displaystyle\sum\limits_{i = 1}^3 {{t_i} = } \dfrac{1}{{2{T_{{H}}}}}\displaystyle\sum\limits_{i = 1}^3 {{w_i}{L_i}} $
,选择各段中最大单位长度重量为
${w_{\max }}$
,进一步加强判定条件
$\displaystyle\sum\limits_{i = 1}^3 {{t_i}} < \dfrac{{{w_{\max }}}}{{2{T_H}}}\sum\limits_{i = 1}^3 {{L_i}} $
,令
$c' = \dfrac{{{T_H}}}{{{w_{\max }}}} = {c_{\min }}$
即各段系泊线中对应最小的悬链线参数,并利用
$\displaystyle\sum\limits_{i = 1}^3 {{L_i}} < L = \sqrt {{S^2} - {z^2}} \left( {S = \sum\limits_{i = 1}^3 {{S_i}} } \right)$
,得到组合系泊线的
$ t' = \dfrac{L}{{2{c_{\min }}}} = \dfrac{{L \cdot {w_{\max }}}}{{2 \cdot {T_H}}} $
。因此,判断条件仍具有与式(4)相同的形式:
|
$ t' < 0.1或{T}_{H} > 5{w}_{\mathrm{max}}L或{{c}}_{\mathrm{min}} > 5L 。$
|
(9) |
当组合系泊线达到式(10)的条件时,可以假设每段系泊线均近似为直线,将每段2个端点的高度差
${z_i}$
作为未知量,利用节点处的竖向分力平衡关系和几何边界条件列方程组进行求解,而无需采用悬链线法求解含有超越函数的方程组,计算过程更加简便。
组合系泊线的求解步骤如下:
步骤1 计算每段系泊线的
${c_i}$
值并找到
${c_{\min }}$
,通过计算得到组合系泊线的
$L$
,利用式(10)判断是否满足条件。
步骤2 假定每一段系泊线上下两端点.的高度差为
${z_i}$
,因此有几何边界条件
$ \displaystyle\sum\limits_{i = 1}^3 {{z_i}} = z $
。利用
${L_i} = \sqrt {s_i^2 - z_i^2} $
和表1中的公式,转化为含待求解未知数
${z_i}$
的表达式。
步骤3 求解每段系泊线两端点
$ {A_i} $
和
${B_i}$
点的张力
${T_{{{{A}}_{{i}}}}}$
、
${T_{{{{B}}_{{i}}}}}$
和竖向分力
${T_{{{V}}{{{A}}_{{i}}}}}$
、
${T_{{{V}}{{{B}}_{{i}}}}}$
。
步骤4 对第
$i$
节点列竖直方向分力的平衡式
$ {T_{{\text{V}}{{\text{A}}_{\text{i}}}}} + {P_i} = {T_{{\text{V}}{{\text{B}}_{{\text{i + 1}}}}}} $
,
${P_i}$
为节点处的集中力。
步骤5 利用力平衡条件和几何约束条件列方程组并求解:
|
$ \left\{ {\begin{aligned} &{{T_{V{A_1}}} + {P_1} = {T_{V{B_2}}}},\\ & {{T_{V{A_2}}} + {P_2} = {T_{V{B_3}}}},\\ &{{z_1} + {z_2} + {z_3} = z} 。\end{aligned}} \right. $
|
(10) |
步骤6 将方程组的解
${z_i}$
代入表1得到对应的张力、竖向分力和角度。
2 影响因素分析 系泊链极限状态受到几何条件(链长
${s_0}$
,水深
$z$
)和外力条件(水平作用力
${T_H}$
,单位长度重量
$w$
)的共同影响,为进一步简化分析条件,通过量纲分析将几何条件和受力条件转化为悬链线参数和垂跨比的条件,并分析其对误差的影响。
2.1 悬链线参数
$c$
的影响
根据文献[7-8],单系泊线的系泊点A和锚点B处的竖向分力有精确解:
|
$ \left\{ {\begin{aligned} {V_{{A}}} = \dfrac{w}{2} \cdot \Bigg(z \cdot \dfrac{{\sqrt {{L^2} + {{\left( {2c} \right)}^2}} }}{L} + {s_0}\Bigg),\\ {V_{{B}}} = \dfrac{w}{2} \cdot \Bigg(z \cdot \dfrac{{\sqrt {{L^2} + {{\left( {2c} \right)}^2}} }}{L} - {s_0}\Bigg)。\\ \end{aligned}}\right. $
|
(12) |
对式(12)和表1中的力计算公式左右同除因子
${T_{{H}}} = w \cdot c$
,并代入
$t = \dfrac{L}{{2c}}$
,无量纲化后得到表2。因此可以得到无量纲化后竖向分力的误差分别为:
$\dfrac{{{T_{{{VA}}}} - {V_{{A}}}}}{{w \cdot c}} = \dfrac{{{T_{{{VB}}}} - {V_{{B}}}}}{{w \cdot c}} = \dfrac{z}{L} \cdot \left( {1 - \sqrt {{t^2} + 1} } \right) + \dfrac{{{s_0}}}{{2c}}$
。当系泊线几何条件(
${s_0}$
,
$z$
,
$L$
)均不变时,随着
$c$
增大
$t$
减小,简化计算的结果更接近理论值,竖向分力的误差趋近于
$\dfrac{1}{2} \cdot w \cdot {s_0}$
。同理,得到张力的简化计算与悬链线理论值的相对误差为
$\dfrac{{{s_0}}}{L} - \sqrt {{{\left( {\dfrac{{z\sqrt {{t^2} + 1} }}{L} - \dfrac{{{s_0}}}{{2c}}} \right)}^2} + 1} $
,且随
$c$
增大误差趋近于0。
表 2(Tab. 2)

表 2 A点和B点的张力无量纲化的结果
Tab. 2 The result of dimensionless force at point A and B
| 无量纲量 |
计算公式 |
|
${T_{ {{VA} } } }$
的无量纲量
|
$\dfrac{ { {T_{ {{VA} } } } } }{ {w \cdot c} } = \dfrac{z}{L} + \frac{ { {s_0} } }{c}$
|
|
${T_{ {{VB} } } }$
的无量纲量
|
$\dfrac{ { {T_{ {{VB} } } } } }{ {w \cdot c} } = \dfrac{z}{L}$
|
|
${V_{{A} } }$
的无量纲量
|
$\dfrac{ { {V_{{A} } } }}{ {w \cdot c} } = \dfrac{z}{L} \cdot \sqrt { {t^2} + 1} + \dfrac{ { {s_0} } }{ {2c} }$
|
|
${V_{{B} } }$
的无量纲量
|
$\dfrac{ { {V_{{B} } } }}{ {w \cdot c} } = \dfrac{z}{L} \cdot \sqrt { {t^2} + 1} - \frac{ { {s_0} } }{ {2c} }$
|
|
表 2 A点和B点的张力无量纲化的结果
Tab.2 The result of dimensionless force at point A and B
|
在外界几何条件不变的情况下,选用
$w$
更大的系泊线,对应满足假设条件时的系泊力将更大。系泊缆相对系泊链的
$w$
更小,因此在同样大小的系泊力作用下更容易达到近似直线的状态。
2.2 垂跨比
$\dfrac{1}{u}$
的影响
令垂跨比
$\dfrac{1}{u} = \dfrac{z}{L}$
,则有
$\dfrac{z}{L} = \dfrac{1}{u}$
,
$\dfrac{{{s_0}}}{L} = \dfrac{{\sqrt {1 + {u^2}} }}{u}$
和
$k = \dfrac{1}{t} = \dfrac{{2c}}{L}$
,对表1中的力计算公式左右同除因子
$w \cdot L$
,无量纲化后得到表3。
表 3(Tab. 3)

表 3 A点和B点的力无量纲化的结果
Tab. 3 The result of dimensionless force at point A and B
| 无量纲量 |
计算公式 |
|
${T_{{\text{VA}}}}$
的无量纲量
|
$ \dfrac{{{T_{{\text{VA}}}}}}{{w \cdot L}} = \dfrac{1}{u} \cdot \dfrac{k}{2} + \dfrac{{\sqrt {1 + {u^2}} }}{u} $
|
|
${T_{{\text{VB}}}}$
的无量纲量
|
$\dfrac{{{T_{{\text{VB}}}}}}{{w \cdot L}} = \dfrac{1}{u} \cdot \dfrac{k}{2}$
|
|
${T_{\text{A}}}$
的无量纲量
|
$\dfrac{{{T_{\text{A}}}}}{{w \cdot L}} = \dfrac{{\sqrt {1 + {u^2}} }}{u} \cdot \dfrac{k}{2} + \dfrac{1}{u}$
|
|
${T_{\text{B}}}$
的无量纲量
|
$\dfrac{{{T_{\text{B}}}}}{{w \cdot c}} = \dfrac{{\sqrt {1 + {u^2}} }}{u} \cdot \dfrac{k}{2}$
|
|
表 3 A点和B点的力无量纲化的结果
Tab.3 The result of dimensionless force at point A and B
|
根据文献[7-8],非线性超越方程
$\dfrac{1}{k} =t = \dfrac{L}{{2c}} = $
$ \sinh \left( \beta \right)$
反映了系泊链总体的刚性平衡,可视为系泊链两端点边界约束的静力平衡关系,因此
$k$
和
$t$
表现为一种系泊链在不同几何条件(
${s_0}$
,
$z$
)和受力条件(
${T_{{H}}}$
,
$w$
)的状态关系。因此只要系泊线具有相同的
$u$
或
$t$
,则均可以视为同一种状态。
当系泊线满足简化计算条件时,假定
$t$
或
$k$
为一个常数,令无量纲函数
${F} \left( u \right) = \dfrac{{\sqrt {1 + {u^2}} }}{u}$
,
${V} \left( u \right) = \dfrac{1}{u}$
。对垂跨比1~
$\dfrac{1}{5}$
(
$u \in \left[ {1,5} \right]$
)的情况进行计算,结果如图5所示。表明当垂跨比减小时(
$u$
增大时),
${F} \left( u \right)$
趋于1,
${V} \left( u \right)$
趋于0。利用表3的关系,可以得到垂跨比减小时,
${T_{{B}}}$
逐渐减小趋于
${T_{{H}}}$
,
${T_{{{VB}}}}$
趋于0。因此在
$z$
不变情况下,应根据锚体的竖向承载能力选择合适的垂跨比,减小竖向分力作用。
3 案例计算 3.1 单系泊线的计算 某锚地水深条件为30 m,选用长度50 m的R3S级别公称规格为
$d = 100\;{\text{mm}}$
的有档系泊链,单位长度质量为219
$ {{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {\text{m}}}} \right. } {\text{m}}} $
,拉力负荷为6480 kN,水下
$w \approx 1.867\;{{{\text{kN}}} \mathord{\left/ {\vphantom {{{\text{kN}}} {\text{m}}}} \right. } {\text{m}}}$
。分别采用悬链线法(方法1)、近似抛物线法(方法2)和简化计算方法(方法3)。相关计算参数见表4。
表 4(Tab. 4)

表 4 相关计算参数
Tab. 4 Table of calculation parameters
| 工况 |
$c/ {\text{m} }$
|
${T_{{H} } }/ { {\text{kN} } }$
|
$t$
|
| 1 |
500 |
933.50 |
0.040 |
| 2 |
1000 |
1867.00 |
0.020 |
| 3 |
1500 |
2800.50 |
0.013 |
| 4 |
2000 |
3734.00 |
0.010 |
| 5 |
2500 |
4667.50 |
0.008 |
|
表 4 相关计算参数
Tab.4 Table of calculation parameters
|
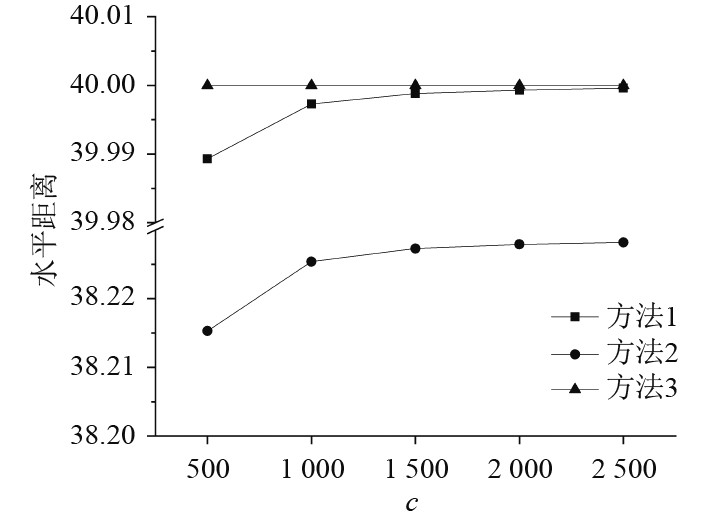
1)水平距离
$l$
的计算结果如图6所示。根据几何近似假设,方法3中A点的水平距离为水平极限距离40 m。随着系泊力作用力增大,方法1和方法2的计算结果逐渐增大,方法3与方法1的相对误差逐渐减小。
2)3种计算方法的点A和点B的张力计算结果如表5和表6所示。方法3得到的
${T_A}$
、
${T_B}$
的计算值均大于方法1理论值,计算值偏于保守。
${T_A}$
平均相对误差为1.02%,
${T_B}$
平均相对误差为1.09%,均小于方法2近似抛物线算法的结果。在拉力负荷范围内,方法3与方法1的相对误差随系泊力增大而减小,与分析结果相一致。
表 5(Tab. 5)

表 5 系泊点A处的张力
Tab. 5 The strain at point A
| 工况 |
c/
$ {\text{m} }$
|
${T_{{H} } }$
/
${ {\text{kN} } }$
|
方法1
${T_{{H} } }/{ {\text{kN} } }$
|
方法2 |
|
方法3 |
|
${T_{{H} } }/{ {\text{kN} } }$
|
相对误差/
%
|
|
${T_{{H} } }/{ {\text{kN} } }$
|
相对误差/
%
|
| 1 |
500 |
933.50 |
1195.94 |
1266.08 |
5.86 |
|
1223.02 |
2.26 |
| 2 |
1000 |
1867.00 |
2362.47 |
2500.26 |
5.83 |
|
2390.01 |
1.17 |
| 3 |
1500 |
2800.50 |
3529.31 |
3734.67 |
5.82 |
|
3557.00 |
0.78 |
| 4 |
2000 |
3734.00 |
4705.74 |
4969.16 |
5.60 |
|
4724.00 |
0.39 |
| 5 |
2500 |
4667.50 |
5863.17 |
6203.69 |
5.81 |
|
5891.00 |
0.47 |
|
表 5 系泊点A处的张力
Tab.5 The strain at point A
|
表 6(Tab. 6)

表 6 系泊点B处的张力
Tab. 6 The strain at point B
| 工况 |
c/
${\text{m} }$
|
${T_{{H} } }$
/
$ { {\text{kN} } } $
|
方法1
${T_{{H} } }/{ {\text{kN} } }$
|
方法2 |
|
方法3 |
|
${T_{{H} } }/{ {\text{kN} } }$
|
相对误差/
%
|
|
${T_{{H} } }/{ {\text{kN} } }$
|
相对误差/
%
|
| 1 |
500 |
933.50 |
1139.92 |
1205.11 |
5.72 |
|
1167.00 |
2.38 |
| 2 |
1000 |
1867.00 |
2306.45 |
2439.17 |
5.75 |
|
2333.99 |
1.19 |
| 3 |
1500 |
2800.50 |
3473.30 |
3673.58 |
5.77 |
|
3500.98 |
0.80 |
| 4 |
2000 |
3734.00 |
4640.21 |
4908.07 |
5.77 |
|
4668.00 |
0.60 |
| 5 |
2500 |
4667.50 |
5807.16 |
6142.60 |
5.78 |
|
5834.99 |
0.48 |
|
表 6 系泊点B处的张力
Tab.6 The strain at point B
|
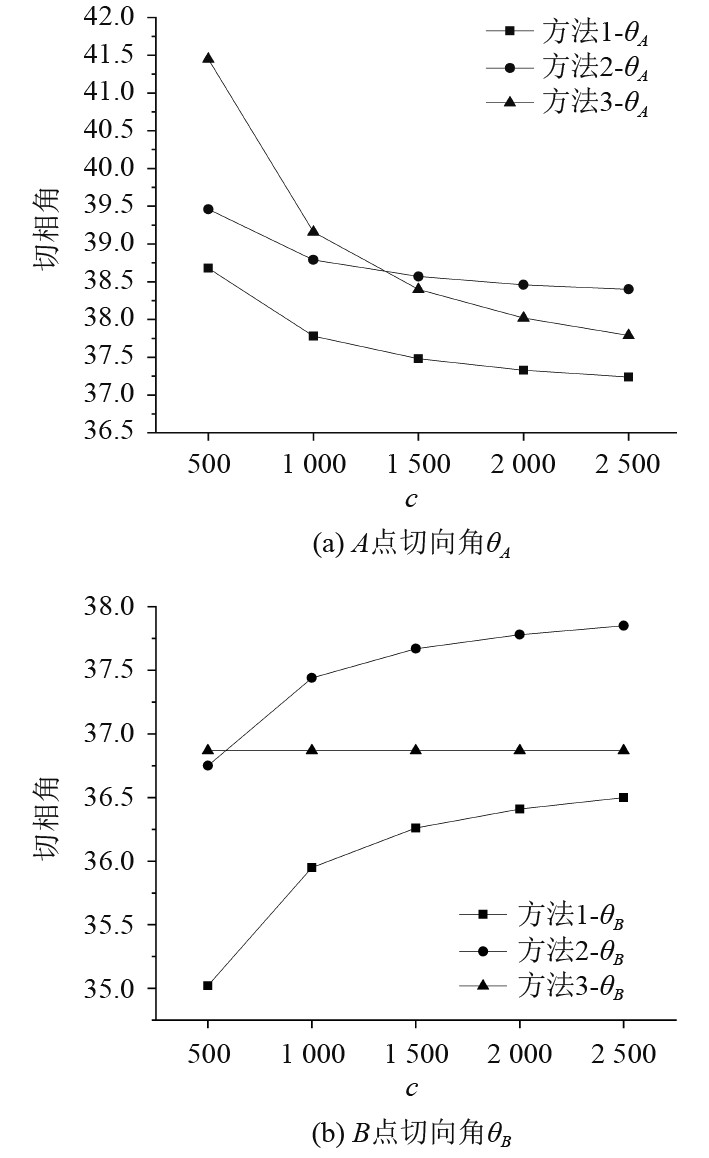
3)切向角计算结果如图7所示。在图7(a)中,随着系泊力增大,3种计算方法的
${\theta _A}$
计算结果逐渐减小,且方法3的计算值逐渐逼近方法1理论值。当
$c > 1\;500$
时,方法3与方法1的相对误差小于方法2的相对误差,表明系泊力越大方法3更加接近理论值。在图7(b)中,由于方法2中对B点切线角
${\theta _{{B}}}$
近似假设为系泊链极限位置的
${\theta _0} \approx 36.87^\circ $
,因此方法3的图像为一条直线。随系泊力增大,方法1和方法2的计算值均呈现逐渐增加的趋势,方法3的计算值逐渐逼近方法1理论值。
3.2 组合系泊线的计算 已知水深条件
${h_1} = 20\;{\rm{m}}$
,锚体埋深
${h_2} = 10\;{\rm{m}}$
。根据国军标[11]要求,确定系泊线相关设计指标如下:系泊链
${S_1}$
段选用R5级别公称直径为100
${\rm{mm}}$
的有档链,拉力负载为9036 kN,链长
${s_1} = 40\;{\text{m}}$
,水下
${w_1} = 1.867\;{{{\text{kN}}} \mathord{\left/ {\vphantom {{{\text{kN}}} {\text{m}}}} \right. } {\text{m}}}$
。
${S_2}$
段选用R5级别公称直径为81 mm的有档链,拉力负载为6179 kN,
${s_2} = 30\;{\rm{m}}$
,水下
${w_2} = 1.225\;{{{\text{kN}}} \mathord{\left/ {\vphantom {{{\text{kN}}} {\text{m}}}} \right. } {\text{m}}}$
。系泊缆选用HMPE材质公称直径为112 mm,破断力为8000 kN,长度
${s_3} = 30\;{\text{m}}$
,
${w_3} \approx 0.08\;{{{\text{kN}}} \mathord{\left/ {\vphantom {{{\text{KN}}} {\text{m}}}} \right. } {\text{m}}}$
。在1节点处为水下重量约
$52.27\;{\text{kN}}$
的重砣,在2节点处为水下重量约
$- 177.63\;{\rm{kN}}$
的GⅠ型浮筒,系泊点A处系泊力
${T_{{H}}} = 2\;500\;{\text{kN}}$
。
分别计算
$t'$
,每段系泊线的上端点位置,系泊点A和锚点B的张力,结果如表7所示。
表 7(Tab. 7)

表 7 相关设计指标
Tab. 7 The strain at point B
| 参数 |
数值 |
参数 |
数值 |
|
$t'$
|
0.037 |
${z_3}/{\rm{m}}$
|
8.57 |
|
${z_1} /{\rm{m}}$
|
11.40 |
${T_A}/{\rm{kN}}$
|
2608.79 |
|
${z_2}/{\rm{m}}$
|
10.03 |
${T_B} /{\rm{kN}}$
|
2608.21 |
|
表 7 相关设计指标
Tab.7 The strain at point B
|
节点1坐标为
$\left( {38.3405,11.4021} \right)$
,节点2坐标为
$\left( {66.6158,21.4271} \right)$
,系泊点A坐标为
$\left( {95.3949,30} \right)$
,近似计算的曲线状态与极限状态的对比如图8所示。表明在满足假设条件的系泊力作用下,防风系泊系统的系泊线构型非常接近于极限直线状态。
在准静态系泊状态下,大型舰船由于鱼尾运动[12],系泊力通常大于1000 kN。尽管在节点增加了集中力,但系泊线状态仍然非常接近直线状态,对于系泊过程中的阵风等突变载荷,系泊链的阻尼作用很小。根据文献[13]中关于系泊系统势能作用对张力影响的分析,可以换用同等破断力等级但弹性更好的系泊缆来增加系统弹性势能储备能力,以增加总势能应对张力在突变载荷作用下的变化,提高阻尼作用,达到削减系泊线张力峰值的目的。
4 结 语 1)采用“以直代曲”的几何近似假设,分析单系泊线在系泊力作用下近似为极限时的直线状态条件,并以此为基础给出单系泊线张力的简化计算方法,避免了求解悬链线理论的超越方程和近似抛物线的非线性方程组。
2)采用分段外推法的思路,将组合系泊线看作由单系泊线结构的组合结构,分析其适用简化计算方法的条件,并给出了求解的步骤。
3)从悬链线参数和垂跨比的角度,分析了受力条件和几何条件对简化计算误差的影响,表明当悬链线参数
$c$
和垂跨比倒数
$u$
增大时,简化计算方法与悬链线理论的张力计算结果的误差减小。
4)通过单系泊线的案例计算,与悬链线法和近似抛物线法进行比较分析,简化计算方法中锚点和系泊点处张力的平均相对误差为1.09%和1.02%,与近似抛物线法相比,与悬链线理论解的相对误差更小。
5)组合系泊线的分析,其计算过程较为简便,能够快速得到设计条件下的张力。




 2023, Vol. 45
2023, Vol. 45
