2. 昆明理工大学 建筑工程学院,云南 昆明 650500
2. Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China
船舶推进系统对船舶朝大型化方向发展起着关键作用。目前常用的船舶推进器主要有:传统的螺旋桨推进器、吊舱式推进器、导管式推进器和泵喷推进器等。每种推进器虽然都有各自的特点,但它们都依靠轴驱动,由于轴的另一侧需延伸至船体或舱体内并与发动机连接,因此,在运行时可能会出现高水平的噪声和振动。为了解决上述传统轴驱动推进系统所带来的问题,近年来提出了一种新型船舶推进系统−轮缘推进器(Rim-driven Thruster,RDT)[1]。该推进器摒弃了轴驱动,取而代之的是用轮缘驱动,即电机系统直接集成到类似导管的外部结构中[2],桨叶直接连接到轮缘上,并在运行时随轮缘一起旋转。因此,轮缘推进器在结构上与导管桨(Ducted Propeller, DP)类似。由于RDT采用轮缘驱动的集成方式,使结构布局更加紧凑,一定程度上降低了噪声振动、节省了舱体空间,也降低了设备安装的难度。此外,RDT的应用范围不仅限于传统船舶,水下机器人(ROV)和自主潜航器(AUV)等特种装置也可以装备高集成的小型RDT,以提高装置的运行性能[3-4]。
现阶段对RDT的研究主要集中在性能优化、流固耦合、振动控制等方面[5]。Sharkh等[6]设计并制造了直径为250mm的RDT,并研究了导管和桨叶截面形状对RDT整体性能的影响。兰加芬等[7]通过单向流固耦合方法对RDT桨叶的强度及变形情况进行了校核。Cai等[8]对RDT的推力及功率进行了分析。宋显成等[9]对RDT的动态启停性能进行了数值模拟研究。然而,相关成果却鲜有涉及RDT流动特点及流动能量损失方面的研究。此外,鉴于RDT在结构上与DP较为相似,现阶段也缺少二者的详细性能对比研究。为此,本文采用计算流体力学方法,并结合熵产理论分析模型对RDT和DP进行数值模拟分析,评估二者的水动力和能量损失分布特点,为RDT和DP的优化设计及能量损失识别分析提供一定的参考依据。
1 数学模型与数值计算方法 1.1 控制方程假设流体不可压缩,控制方程包括连续方程和动量方程。雷诺时均的纳维斯托克斯方程可表示为:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho {{\overline {{{u'}_i}u'} }_j}} \right] + {f_i} 。$ | (2) |
式中:ui为时均速度;p为流体时均压力;ρ为流体密度;μ为流体动力黏度;fi为体积力分量。
1.2 敞水参数敞水性能可定义为无量纲参数:进速系数(J)、推力系数(KT)、扭矩系数(KQ)、效率(η),分别由下式计算得到:
| $ J = \frac{{{V_A}}}{{nD}} ,$ | (3) |
| $ {K_T} = \frac{T}{{\rho {n^2}{D^4}}},$ | (4) |
| $ {K_Q} = \frac{Q}{{\rho {n^2}{D^5}}},$ | (5) |
| $ \eta = \frac{{{K_T}}}{{{K_Q}}} \cdot \frac{J}{{2\text{π} }} 。$ | (6) |
式中:T,Q,ρ,n,D,VA分别表示推力、扭矩、流体密度、转速、桨叶直径、进速。
1.3 熵产理论与计算方法熵产理论是热力学第二定律的一种形式,主要用于描述能量转换过程中的耗散效应,即任何能量转换过程中均存在不可避免的熵增量(损失效应)。船舶推进器在运行时,旋转的桨叶作绕流运动并对水流做功的过程也是一个不可逆过程,因此也必然存在不可逆的能量诱发损失。此外,由于水的比热容很高,在本文RDT与DP的流场计算过程中,认为温度是恒定不变的,不考虑传热过程所引起的熵产。
当忽略传热的影响时,RDT和DP的能量损失主要由流体黏性所引起的耗散和湍流流动所引起的耗散所组成[10-11]。由黏性耗散所引起的熵产率(W·m−3·K−1)为:
| $\begin{aligned}[b] {\dot S_{\bar D}}^{\prime \prime \prime } = &\frac{\mu }{T}\Bigg[ {{\left( {\frac{{\partial \bar u}}{{\partial y}} + \frac{{\partial \bar v}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial \bar u}}{{\partial z}} + \frac{{\partial \bar w}}{{\partial x}}} \right)}^2} + {\Bigg( {\frac{{\partial \bar v}}{{\partial z}} + \frac{{\partial \bar w}}{{\partial y}}} \Bigg)}^2 \Bigg] + \\ &\frac{{2\mu }}{T}\left[ {{{\left( {\frac{{\partial \bar u}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial \bar v}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial \bar w}}{{\partial z}}} \right)}^2}} \right] ,\end{aligned}$ | (7) |
由湍流耗散所引起的熵产率(W·m−3·K−1)为:
| $\begin{aligned}[b] {\dot S_{D'}}^{\prime \prime \prime } = &\frac{\mu }{T}\left[ {{{\left( {\frac{{\partial u'}}{{\partial y}} + \frac{{\partial v'}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial u'}}{{\partial z}} + \frac{{\partial w'}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v'}}{{\partial z}} + \frac{{\partial w'}}{{\partial y}}} \right)}^2}} \right] +\\ & \frac{{2\mu }}{T}\left[ {{{\left( {\frac{{\partial u'}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v'}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial w'}}{{\partial z}}} \right)}^2}} \right]。\end{aligned} $ | (8) |
式中:
然而,对于雷诺时均的纳维斯托克斯方程,脉动速度u′,v′,w′无法直接求解得到。根据Kock等[11]的研究,在SST k-ω湍流模型中,由湍流引起的熵产率可改写为:
| $ {\dot S_{D'}}^{\prime \prime \prime } = \beta \frac{{\rho \omega k}}{T}。$ | (9) |
式中:β=0.09;ω为湍动能耗散率;k为湍流强度。
对上述2种熵产率分别进行体积分,可以得到黏性耗散熵产SDV(W/K)和湍流耗散熵产SDT(W/K):
| $ {S_{DV}} = \int\limits_V {{{\dot S}_{\bar D}}^{\prime \prime \prime }}{\rm{ d}}V,$ | (10) |
| $ {S_{DT}} = \int\limits_V {{{\dot S}_{D'}}^{\prime \prime \prime }} {\rm{d}}V,$ | (11) |
整个流体计算域的总熵产为:
| $ {S_D} = {S_{DV}} + {S_{DT}}。$ | (12) |
以荷兰实验室的Ka4-7010+19A四叶DP为研究原型,具体参数见表1。RDT在DP的基础上稍作调整,在保持桨叶与导管尺寸、形状及相对装配位置不变的前提下,去除桨叶轮毂部分,用轮缘连接桨叶,轮缘宽度比叶尖翼型的轴向跨度略大。二者的三维模型如图1所示。
|
|
表 1 DP参数 Tab.1 The parameters on the DP |

|
图 1 DP与RDT的三维模型 Fig. 1 Three-dimensional model of the DP and RDT |
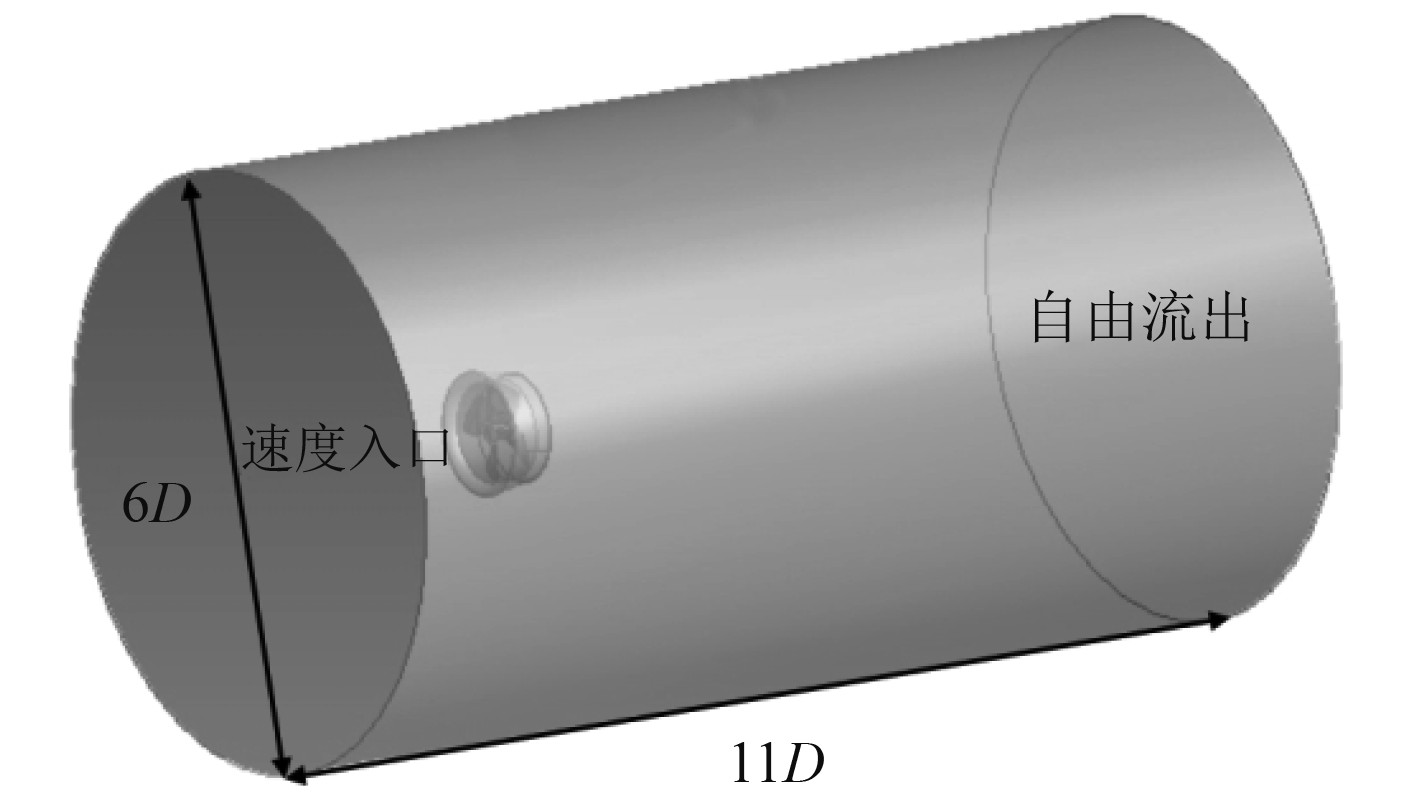
模型计算域如图2所示。速度入口位于推进器中心上游3D的距离,自由流出出口位于推进器中心下游8D的距离,外边界为自由滑移。RDT与DP设置为固壁面无滑移条件。计算区域设置为静止域和旋转域,其中旋转域交界面采用interface设置。采用非结构网格对模型及计算域进行网格划分,对RDT及DP附近网格进行网格加密,并设置边界层网格。此外,对DP在J=0.4条件下进行网格数无关验证,如表2所示,当网格数超过400万后KT和10KQ基本不变,最终采用网格数为600万的设置进行后续计算。
|
图 2 模型计算域 Fig. 2 Model calculation domain |
|
|
表 2 网格数无关验证 Tab.2 Mesh independence assessment results |
根据荷兰实验室[12-13]公开的试验数据,表3给出了DP的敞水性能的计算结果和实验数据的对比。可以看出两者的吻合度较好,验证了本文数值模型及方法的可靠性。
|
|
表 3 DP敞水性能的计算值与实验值对比 Tab.3 Comparison of numerical results and experimental results on the open water performance of the DP |
图3为DP与RDT之间的敞水性能比较。可以看出,DT在所有进速下的推力系数与扭矩系数均高于DP。一方面,在轮缘的作用下,RDT将提供更大的推力,而另一方面,轮缘也额外产生了一定的附加扭矩,导致RDT的扭矩要明显高于DP。最终的效果是RDT在整个进速条件下的效率要低于DP。以本文讨论的设计工况为例,当J=0.4时,DP的KT=0.298,10KQ=0.391,η=0.486;RDT的KT=0.319,10KQ=0.452,η=0.449。即,RDT的KT和10KQ分别比DP高出7.05% 和15.60%,而η比DP低出7.61%。因此,即使采用相同的螺旋桨和导管模型,RDT与DP也存在明显的水动力性能差异。

|
图 3 敞水性能对比 Fig. 3 Open water performance comparison between the DP and the RDT |
桨叶迎流面与背流面之间的压力差是螺旋桨产生推力和扭矩的主要因素。图4为P与RDT在J=0.4下桨叶与导管附近的局部压力分布情况。可以看出,两者的迎流面的低压分布存在明显的区别,而背流面的高压分布较为类似。其中,DP的迎流面低压区沿叶尖至桨毂方向不断扩大,桨毂附近存在一个压力极低的小范围区域。RDT的迎流面低压区分布正好与DP相反,低压区沿轮毂至轮缘方向不断扩大,轮缘附近存在一个压力极低的小范围区域。由于RDT的低压区更多的集中在轮缘附近,从而产生更大的推力和扭矩,这解释了RDT相比DP获得较高的推力系数与扭矩系数的原因。需要指出的是,由于DP存在叶尖间隙,高速旋转的桨叶与导管内壁相互作用导致了间隙区域存在较强的泄流效应,而从图4中也可以清楚地观察到叶尖区域存在明显的压力梯度。另一方面,由于RDT不存在叶尖间隙,因此不存在叶尖泄流。然而,RDT中轮缘和导管的连接处间隙也会出现流动现象,旋转的轮缘与静止的导管连接面之间的间隙流动类似于2个同心圆环之间的相互作用。因此,高速旋转下的轮缘间隙将存在明显的摩擦和湍流流动,导致间隙处的压力很高,并产生了显著的扭矩。图5为DP与RDT在J=0.4下轴向速度分布情况。可以看出,二者的尾流形态呈现均匀的对称分布,导管内侧后缘均出现一定的流动分离现象。此外,由于DP具有桨毂结构,一部分来流被桨毂阻塞而形成一定范围的毂涡低速区。而RDT由于没有桨毂,轴心处的开放缺口允许一部分来流自由通过。因此,RDT的轴心速度明显高于DP。

|
图 4 压力分布 Fig. 4 Pressure distribution |

|
图 5 轴向速度分布 Fig. 5 Axial velocity distribution |
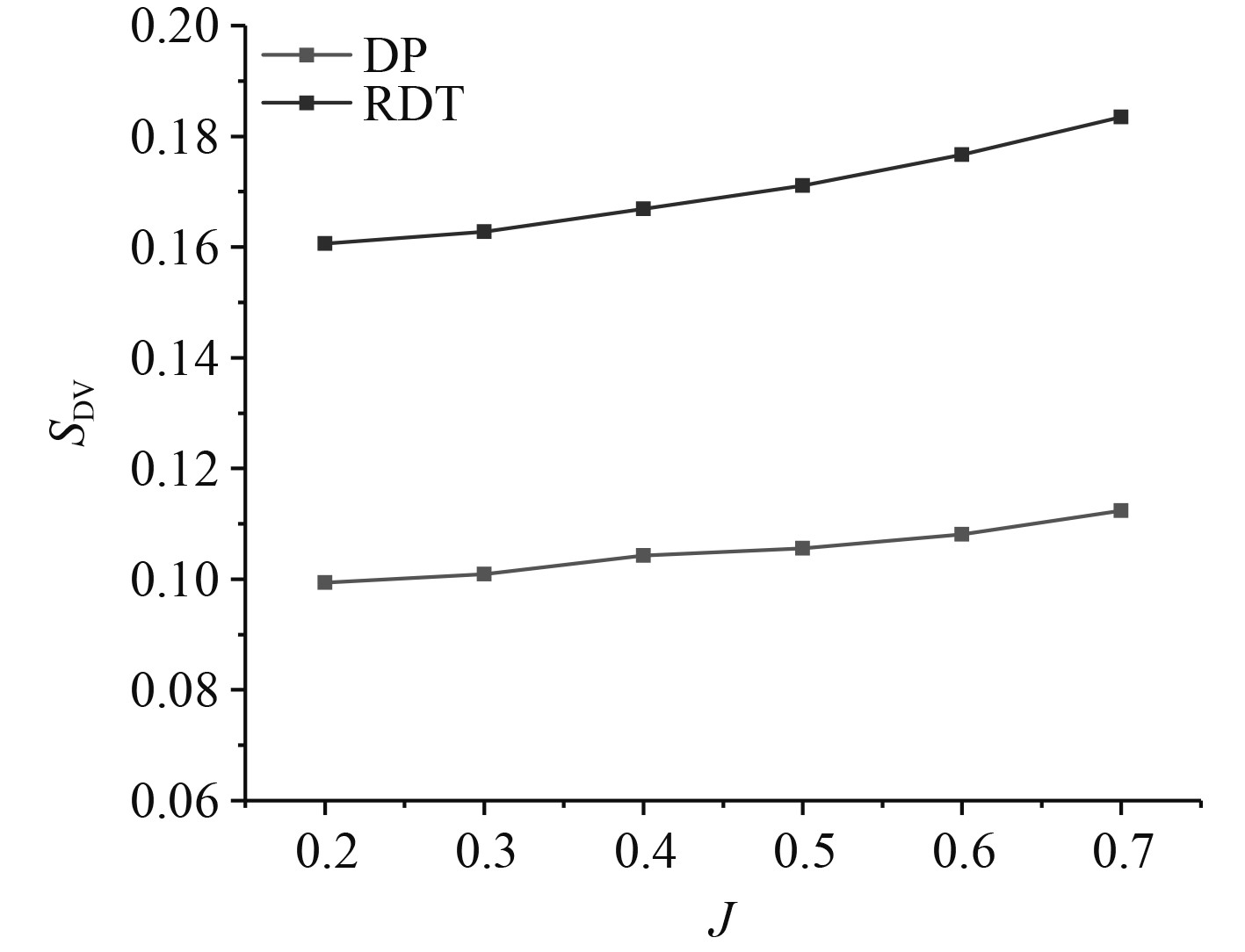
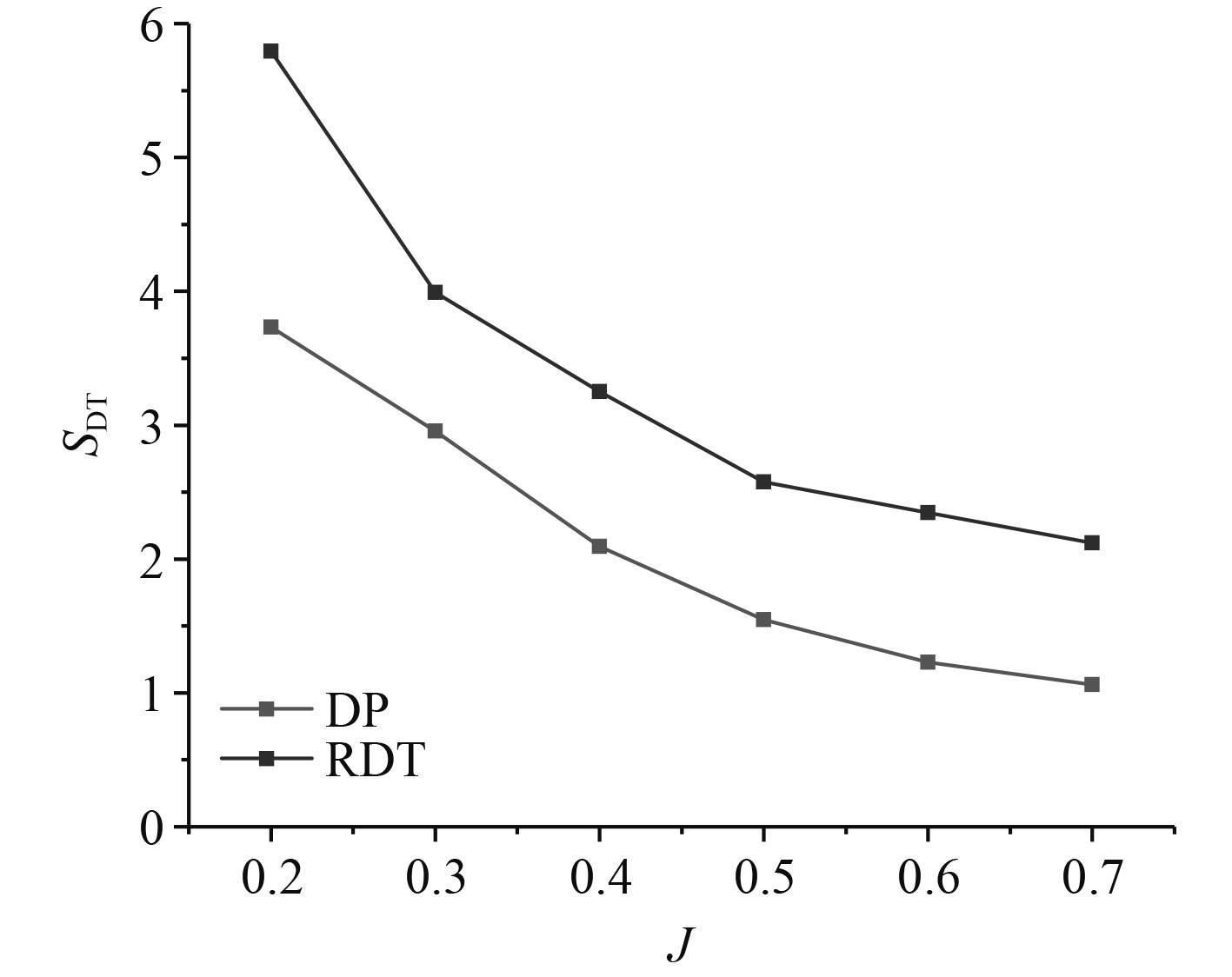
图6和图7分别为DP与RDT之间的黏性耗散熵产及湍流耗散熵产比较。可以看出,二者的SDV均随着进速的增大而增大,而SDT均随着进速的增大而减小。随着进速的增大,桨叶附近的速度梯度的变化明显,流体内摩擦效应增强,导致黏性力增大。因此,SDV随进速的增大而增大,但由于黏性力变化有限,SDV在整个进速范围内变化幅度很小。而由于高速旋转的桨叶在低进速条件下将迫使周边流体进行较强的动量交换运动并出现了大量的湍流流动,从而导致了较大的能量损失[14]。而随着进速的不断增加,该动量交换运动的强度逐渐减弱。因此,SDT随进速的增大而减小,且在整个进速范围内变化幅度很大。此外,二者所对应的SDT均远远高于SDV。在全进速范围内,二者各自的SDV占总熵产的比值均超过95%。因此,湍流耗散是引起不可逆能量损失的主导因素。同时值得注意的是,RDT在全进速范围内的SDV与SDT均高于DP。同样以J=0.4为例,DP的SDV=0.104,SDT= 2.092;RDT的SDV=0.167,SDT= 3.250。即RDT的SDV和SDT分别DP高出60.58%和55.35%。
|
图 6 黏性耗散熵产对比 Fig. 6 Comparison on the viscous dissipation entropy production |
|
图 7 湍流耗散熵产对比 Fig. 7 Comparison on the turbulence dissipation entropy production |
图8为DP与RDT在J=0.4下的流场总熵产率分布情况。可以看出,在桨叶与导管的相互作用下,二者的导管内侧后缘处均出现了一定范围的能量损失,这与图5中该位置出现的流动分离现象所吻合。该损失区域不断向下游延伸,且呈现出先放宽而后收缩的态势。但二者的能量损失分布也存在一定的差异。一方面,由于DP桨毂后端出现了明显的毂涡低速区,该毂涡低速区也导致了较为明显的能量损失,而RDT的轴心后端的能量损失并不明显。因此,RDT的开放缺口对于减少轴心处的能量损失具有明显优势。另一方面,由于RDT中的轮缘间隙存在明显的摩擦和湍流效应,这也导致了该区域附近产生极大的能量损失。因此,虽然RDT能有效减少和抑制轴心处的能量损失,但无法避免由轮缘所引起的能量损失。最终的效果是RDT在整个进速条件下的SDV和SDT均高于DP。此外,可以看出能量损失的产生与流场中的不良流动因素密切相关,如流动分离、流动摩擦、涡流等,而本文所引入的熵产理论分析能够较好地捕获这些损失特征区域,并量化衡量损失的严重程度。

|
图 8 总熵产率分布 Fig. 8 Total entropy production rate distribution |
本文采用计算流体力学方法和熵产理论分析方法对RDT和DP的水动力和能量损失特性进行详细对比研究,得到如下结论:
1)RDT在全进速范围内比DP具有更高的推力与扭矩,但效率却低于DP。二者的SDV均随着进速的增大而增大,而SDT均随着进速的增大而减小。同时,二者各自所对应的SDT均远远高于SDV(占比超过95%)。因此,湍流耗散是引起不可逆能量损失的主导因素。
2)由于DP具有桨毂结构,一部分来流被桨毂阻塞而形成一定范围的毂涡低速区。该毂涡低速区也造成了较为明显的能量损失。而RDT没有桨毂,轴心处的开放缺口允许一部分来流自由通过,其轴心后端的能量损失并不明显。因此,RDT的开放缺口对于减少轴心处的能量损失具有明显优势。然而,RDT能有效减少和抑制轴心处的能量损失,但无法避免由轮缘所引起更为显著的能量损失,最终的效果是RDT在全进速条件下的熵产均高于DP。
3)能量损失的产生与流场中的不良流动因素密切相关,如流动分离、流动摩擦、涡流等,本文所引入的熵产理论分析能够较好地捕获这些损失特征区域,并量化衡量损失的严重程度。此外,通过熵产分析可以深入地了解不同能量损失的诱导机制,可为RDT及DP提供更好的优化设计方法。
| [1] |
TUOHY P M, SMITH A C, HUSBAND M. Induction rim-drive for a marine propulsor[R]. MO251, 2010.
|
| [2] |
谈微中, 严新平, 刘正林, 等. 无轴轮缘推进系统的研究现状与展望[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(3): 601-605. TAN Wei-zhong, YAN Xin-ping, LIU Zheng-lin, et al. Technology development and prospect of shaftless Rim-driven propulsion system[J]. Journal of Wuhan University of Technology (Transportation Science and Engineering), 2015, 39(3): 601-605. |
| [3] |
SHEN Y, HU P, JIN S, et al. Design of novel shaftless pump-jet propulsor for multi-purpose long-range and high-speed autonomous underwater vehicle[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-4. |
| [4] |
SHARKH S M, LAI S H. Slotless PM brushless motor with helical edge-wound laminations[J]. IEEE Transactions on Energy Conversion, 2009, 24(3): 594-598. DOI:10.1109/TEC.2009.2025423 |
| [5] |
YAN X P, LIANG X G, WU O Y, et al. A review of progress and applications of ship shaft-less rim-driven thrusters[J]. Ocean Engineering, 2017, 144: 142-156. DOI:10.1016/j.oceaneng.2017.08.045 |
| [6] |
SHARKH S M, TURNOCK S R, DRAPER G. Performance of a tip-driven electric thruster for unmanned underwater vehicles[C]//The Eleventh International Offshore and Polar Engineering Conference. OnePetro, 2001.
|
| [7] |
兰加芬, 欧阳武, 严新平. 无轴轮缘推进器水动力性能分析及桨叶强度校核[J]. 船舶工程, 2018, 40(10): 52-58. LAN Jia-fen, OUYANG Wu, YAN Xin-ping. Hydrodynamic performance analysis and blade strength verification of shaftless rim-driven thruster[J]. Ship Engineering, 2018, 40(10): 52-58. DOI:10.13788/j.cnki.cbgc.2018.10.052 |
| [8] |
CAI M, YANG C, WU S, et al. Hydrodynamic analysis of a rim-driven thruster based on RANS method[C]//OCEANS 2015-MTS/IEEE Washington. IEEE, 2015: 1-5.
|
| [9] |
宋显成, 左哲清, 赵国平, 等. 船舶无轴轮缘推进动态特性数值研究[J]. 舰船科学技术, 2021, 43(11): 46-52. SONG Xian-cheng, ZUO Zhe-qing, ZHAO Guo-ping, et al. Numerical study on dynamic characteristics of ship shaftless rim-driven propulsion[J]. Ship Science and Technology, 2021, 43(11): 46-52. DOI:10.3404/j.issn.1672-7649.2021.06.009 |
| [10] |
KOCK F, HERWIG H. Entropy production calculation for turbulent shear flows and their implementation in CFD codes[J]. International Journal of Heat and Fluid Flow, 2005, 26(4): 672-680. DOI:10.1016/j.ijheatfluidflow.2005.03.005 |
| [11] |
KOCK F, HERWIG H. Local entropy production in turbulent shear flows: a high-Reynolds number model with wall functions[J]. International Journal of Heat and Mass Transfer, 2004, 47(10): 2205-2215. |
| [12] |
OOSTERVELD M W C. Wake Adapted Ducted Propellers[M]. Bl^Llothclk der Technische Hogeschool Delft. 1970.
|
| [13] |
OOSTERVELD M W C. Ducted Propeller Characteristics[C]// RINA Symposium on Ducted Propellers. 1973.
|
| [14] |
宋科, 杨邦成. 基于熵产理论的导管桨流动损失特性[J]. 中国舰船研究, 2022, 17(2): 91-97. SONG Ke, YANG Bang-cheng. Flow energy loss characteristics of ducted propeller using entropy production theory[J]. Chinese Journal of Ship Research, 2022, 17(2): 91-97. |
 2023, Vol. 45
2023, Vol. 45
