在研究船桨舵相互干扰[1-3],或者对带有推进器的船体[4-5]、潜艇或者其他水下航行器进行操纵性能预报时,一种方法是对研究对象的几何模型进行网格划分以求解真实流场中的操纵运动[6];另一种方法是建立体积力模型,将与螺旋桨的推力和力矩等效的体积力施加给螺旋桨叶片作用区域的网格单元,进而对控制方程进行求解计算[7-10]。在对船舶、潜艇以及其他水下航行器进行操纵性能预报过程中,回转半径、转弯角速度、操纵装置控制下的系统响应情况、研究对象的稳定程度往往是被关注的重点,对真实几何划分网格或者对研究对象施加体积力往往具有近似相同的效果。
研究泵喷推进器的推进能力时将其划分为转子系统、导管系统、定子系统[11-12],其推力系数、转矩系数可以表示为这三者之和。当已知导管几何以及推进器敞水性能参数后,可通过体积力换算求解虚拟盘体相关尺寸,进而将体积力施加到虚拟盘体上以模拟真实的几何所产生的推力和转矩。
由于导管的存在,推进器的推进能力往往得到了较大幅度提升,当推进器处于一定来流速度的流场中时,进入推进器的水流在转子以及导管的相互作用下加速从出口喷出。在导管内部建立虚拟盘体,对其施加体积力源项[10-11],使得等效体积力和真实叶片几何作用下推进器导管内水流的动量变化对应的推力和转矩相同,可以有效减小对推进器真实几何模型推进性能数值模拟时的计算开销,提高船舶、潜艇以及水下航行器有动力推进情况下的数值自航、操纵性预报效率。
1 准稳态假设条件下航行器推进器的耦合流场数值模拟模型对推进器性能进行研究时,首要研究推进器的敞水性能。而航行器在运动过程中,尤其是机动过程中,推进器及航行器之间的相互耦合作用更加明显[13-15],因此对于航行器及推进器的耦合流场数值模拟建立在准稳态假设条件下,研究准稳态条件下推进器包含定子、转子和导管3个部件的力矩系数、推力系数与进速系数之间的关系。
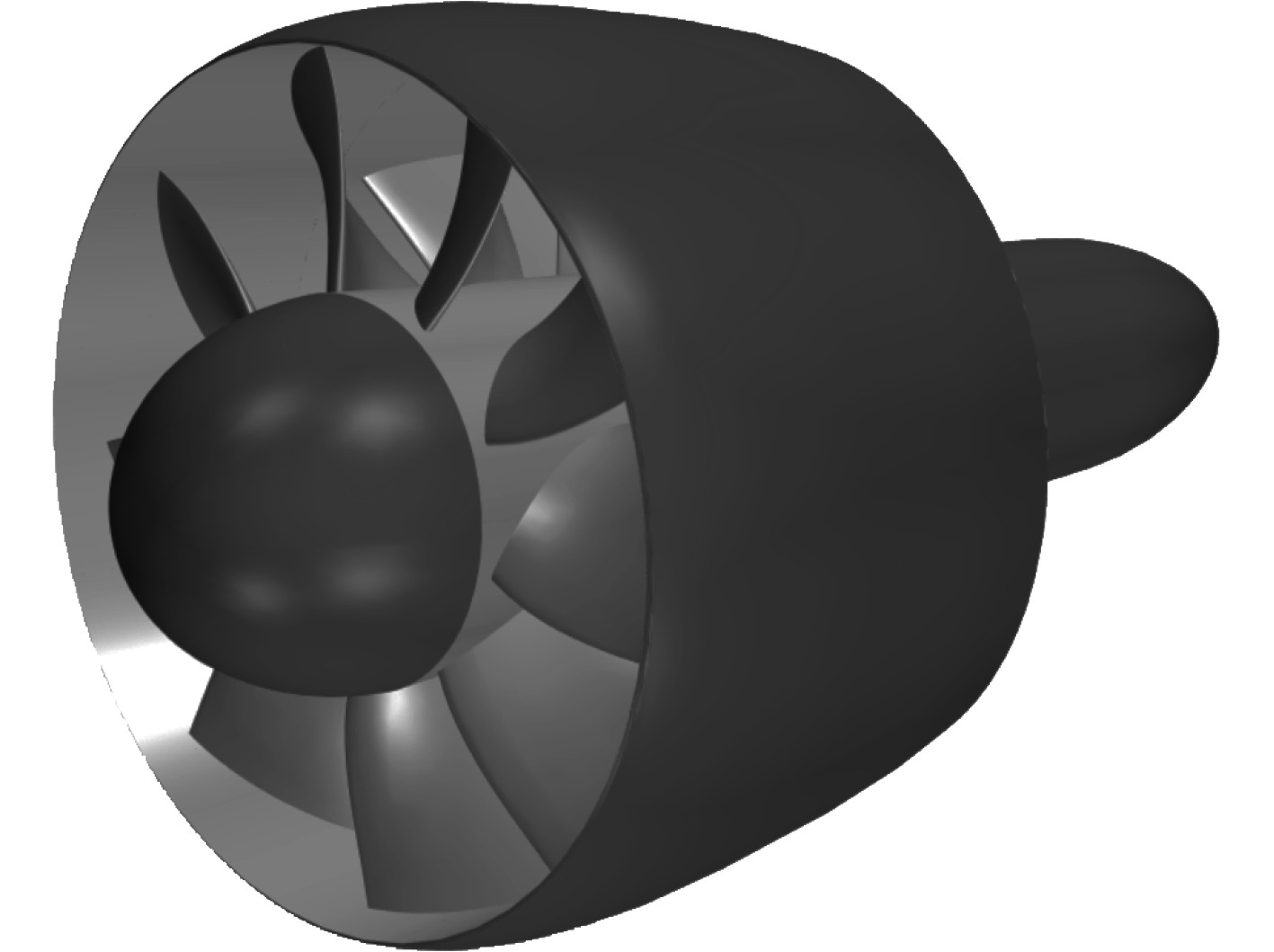
1.1 几何模型本文以某型航行器推进器为研究对象进行数值模拟及验证。为了简化计算模型,将推进器简化为具有头部和尾部导流帽的推进部分,只保留导管、转子和定子,几何模型如图1所示。
|
图 1 推进器几何模型 Fig. 1 Geometrical model of thruster |
1)控制方程
对不可压缩流体数值求解涉及质量守恒、动量守恒、能量守恒的N-S方程,其连续性方程和动量方程如下式:
| $ \begin{split} &\frac{{\partial U}}{{\partial t}} + \frac{{\partial {F_1}(U)}}{{\partial x}} + \frac{{\partial {F_2}(U)}}{{\partial y}} + \frac{{\partial {F_3}(U)}}{{\partial z}} = \\ &\frac{{\partial {G_1}}}{{\partial x}} + \frac{{\partial {G_2}}}{{\partial y}} + \frac{{\partial {G_3}}}{{\partial z}}。\\[-10pt] \end{split} $ | (1) |
式中:
| $\begin{aligned} U = {\left[ {\rho ,\rho u,\rho v,\rho w,E} \right]^{\rm{T}}},\end{aligned} $ |
| $\begin{aligned} p = \rho RT,\end{aligned} $ |
| $\begin{aligned} {F_1}(U) = {\left[ {\rho u,\rho {u^2} + p,\rho uv,\rho uw,u(E + p)} \right]^{\rm{T}}},\end{aligned} $ |
| $\begin{aligned} {F_2}(U) = [ \rho v,\rho uv,\rho {v^2} + p, \rho vw,v(E + p) ]^{\rm{T}},\end{aligned} $ |
| $\begin{aligned} {F_3}(U) = {\left[ {\rho w,\rho wu,\rho wv,\rho {w^2} + p,w(E + p)} \right]^{\rm{T}}},\end{aligned} $ |
| $\begin{aligned} {G_1}(U) = {\left[ {0,{\tau _{11}},{\tau _{12}},{\tau _{13}},k\dfrac{{\partial T}}{{\partial x}} + u{\tau _{11}} + v{\tau _{12}} + w{\tau _{13}}} \right]^{\rm{T}}},\end{aligned} $ |
| $\begin{aligned} {G_2}(U) = {\left[ {0,{\tau _{21}},{\tau _{22}},{\tau _{23}},k\dfrac{{\partial T}}{{\partial y}} + u{\tau _{21}} + v{\tau _{22}} + w{\tau _{23}}} \right]^{\rm{T}}},\end{aligned} $ |
| $\begin{aligned} {G_3}(U) = [ 0, {\tau _{31}},{\tau _{32}},{\tau _{33}}, k \dfrac{{\partial T}}{{\partial z}} + u{\tau _{31}} + v{\tau _{32}} + w{\tau _{33}} ]^{\rm{T}}。\end{aligned} $ |
| $\begin{aligned} {\tau _{ij}} = \left\{ {\begin{array}{*{20}{l}} {\mu \Bigg(\dfrac{{\partial {u_i}}}{{\partial {x_j}}} + \dfrac{{\partial {u_j}}}{{\partial {x_i}}}\Bigg),\begin{array}{*{20}{l}} {}{} \end{array}i \ne j} ,\\ {\mu \Bigg(2\dfrac{{\partial {u_i}}}{{\partial {x_i}}} - \dfrac{2}{3}divV\Bigg),i = j} 。\end{array}} \right.\end{aligned} $ |
其中:
2)流体域网格划分
外流场前部和后部长度分别为5倍和10倍导管入口直径,径向尺寸为10倍导管入口直径,具体流体域尺寸如图2所示。

|
图 2 流体域网格划分 Fig. 2 Grid division of fluid domain |
将流体域划分为转子区域,定子区域和外流场区域,对转子和定子区域以及推进器尾流区域进行加密,为保证交界面网格的正交性,在每个区域的交界面设置1层边界层网格。推进器网格划分结果如图3所示。

|
图 3 推进器真实几何网格划分 Fig. 3 Real geometric mesh generation of thruster |
实质上,泵喷推进是通过导管、定子、转子相互作用增加推进器进流口和出流口的喷速比来产生较高推进性能的,仿真时,可采用施加体积力的虚拟盘代替真实叶片几何模拟推进器的推进性能。
2.1 控制方程体积力流动控制方程包括连续方程和动量方程:
| $ \left\{ \begin{aligned} &\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0,\\& \frac{{\partial {u_i}}}{{\partial t}} + {u_j}\frac{{\partial {u_j}}}{{\partial {x_j}}} = - \frac{{\partial \hat p}}{{\partial {x_i}}} + \frac{1}{{{R_e}}}\frac{{{\partial ^2}{u_i}}}{{\partial {x_j}\partial {x_j}}} - \frac{\partial }{{\partial {x_i}}}\overline {{{u'}_i}{{u'}_j}} + f_i^*。\end{aligned} \right. $ | (2) |
式中:
构建体积力源项时,不考虑叶片真实几何结构,设置体积力轴向均匀分布于圆柱体虚拟盘上,在径向遵循 Goldstein 的最佳分布。因此可以在已知进速系数、推力系数、转矩系数的前提下求解虚拟盘体产生的等效推力和力矩,或者在已知推力和转矩的情况下求解推力系数和转矩系数,因此在构建虚拟盘模型时不需要考虑推进器的叶片真实几何参数,体积力表达形式如下:
| $ {f_{bx}} = {A_x}r*\sqrt {1 - r*} ,$ | (3) |
| $ {f_{b\theta }} = {A_\theta } \cdot \frac{{r*\sqrt {1 - r*} }}{{r*(1 - {{r'}_h}) + {{r'}_h}}}。$ | (4) |
式中:
| $\begin{aligned} & r* = \frac{{r' - {{r'}_h}}}{{1 - r'}} \text{,} \end{aligned} $ |
| $\begin{aligned} {r'_h} = \frac{{{R_H}}}{{{R_P}}} \text{,} \end{aligned} $ |
| $\begin{aligned} r' = \frac{r}{{{R_P}}} \text{,} {A_x} = & \frac{{105}}{8} \cdot \frac{T}{{\text{π} \Delta (3{R_H} + 4{R_P})({R_P} - {R_H})}} \text{,} \end{aligned} $ |
| $\begin{aligned} {A_\theta } = & \frac{{105}}{8} \cdot \frac{Q}{{\text{π} \Delta {R_P}(3{R_H} + 4{R_P})({R_P} - {R_H})}}。\end{aligned} $ |
其中:
对于给定几何的泵喷推进器,当外流场和推进器相关性能参数已知时,可以根据动量定理计算体积力虚拟盘体的尺寸,作用位置以及相关性能参数。当已知真实推进器敞水性能后可以通过等价变化得到虚拟盘体一定进速系数下的推力系数、转矩系数。
虚拟盘流动模型示意图如图4所示。

|
图 4 虚拟盘流动模型示意图 Fig. 4 Schematic diagram of virtual disk flow model |
当已知推进器的转速和进流速度以及盘面直径时,可以得到推进器的进速系数。为保证虚拟盘的外壁面和导管不相交,盘体外径应略小于真实叶片几何。当转速和入流条件相同时,盘体的进速系数、推力系数、转矩系数进行相应换算。
记推进器叶片和盘体直径分别为
假设推进器转子、定子和导管推力分别为
| $ {K_{TRS}} = {T_R} + {T_S},$ | (5) |
推进器总推力系数为:
| $ {K_{TPJP}} = {T_R} + {T_S} + {T_D} ,$ | (6) |
推进器转子的转矩和转矩系数分别为
| $ {T_{PJP}} = {K_{TRS}}\rho {n^2}D_{PJP}^4 ,$ | (7) |
| $ {Q_{PJP}} = {K_{QPJP}}\rho {n^2}D_{PJP}^5,$ | (8) |
| $ J = \frac{V}{{nD}} 。$ | (9) |
当虚拟盘体尺寸和真实叶片几何有所不同时,需对盘体的推进系数、转矩系数以及进速系数进行转换,为保证盘体所产生的推力和转矩与真实推进器转子和定子系统的推力和转矩相同,通过等价变换可以得到当转速相同条件下盘体的水力性能参数和推进器转子、定子系统的关系为:
| $ {J_P} = \frac{V}{{n{D_P}}} ,$ | (10) |
| $ {K_{TP}} = {K_{TRS}} \cdot {\left( {\frac{{{D_{PJP}}}}{{{D_P}}}} \right)^4},$ | (11) |
| $ {K_{QP}} = {K_{QPJP}} \cdot {\left( {\frac{{{D_{PJP}}}}{{{D_P}}}} \right)^5},$ | (12) |
联立式(7)~式(12)可以得到虚拟盘体能够产生的等效推力和转矩:
| $ {T_P} = \frac{{\rho {K_{TP}}V_{PIN}^2D_P^2}}{{J_P^2}},$ | (13) |
| $ {Q_P} = \frac{{\rho {K_{QP}}V_{PIN}^2D_P^3}}{{J_P^2}}。$ | (14) |
式中:
在流体域网格划分基础上,对推进器真实几何推进性能及替代方案推进性能进行仿真分析。对叶片几何,设定推进器进速系数变化范围为0.8~2,间隔为0.2进行模拟,来流速度分别为1.2694 m/s、1.5867 m/s、1.904 m/s、2.2214 m/s、2.5387 m/s、2.856 m/s、3.1734 m/s。
对替代方案,由于虚拟盘体为圆柱体,为保证盘体的网格和导管不重叠,虚拟盘的直径应略小于真实叶片直径,因此在进行仿真时,相同来流条件下虚拟盘的进速系数大于真实叶片的进速系数,当要产生相同推力和力矩时虚拟盘的推力系数和转矩系数需要按照式(10)~式(12)进行等价转换,当真实泵喷推进器进速系数从0.8变化至2时虚拟盘对应的进速系数、推力系数、转矩系数和原推进器的敞水性能参数有所不同,替代方案进速系数分别为0.8635、1.0794、1.2953、1.5111、1.7270、1.9429、2.1588。
3.2 虚拟盘体参数及网格划分设置虚拟盘位于推进器转子叶片区域,结合叶片真实几何数值模拟结果和试验结果,通过等价变换,得到替代方案虚拟盘体厚度0.06 m,外径0.105 m,内径0.055 m,进流面距离虚拟盘前端面0.02 m。选择和真实推进器相同的速度入口作为虚拟盘的进流平面,虚拟盘和导管、轮毂区域网格如图5所示。

|
图 5 虚拟盘体网格划分 Fig. 5 Grid division of virtual disk |
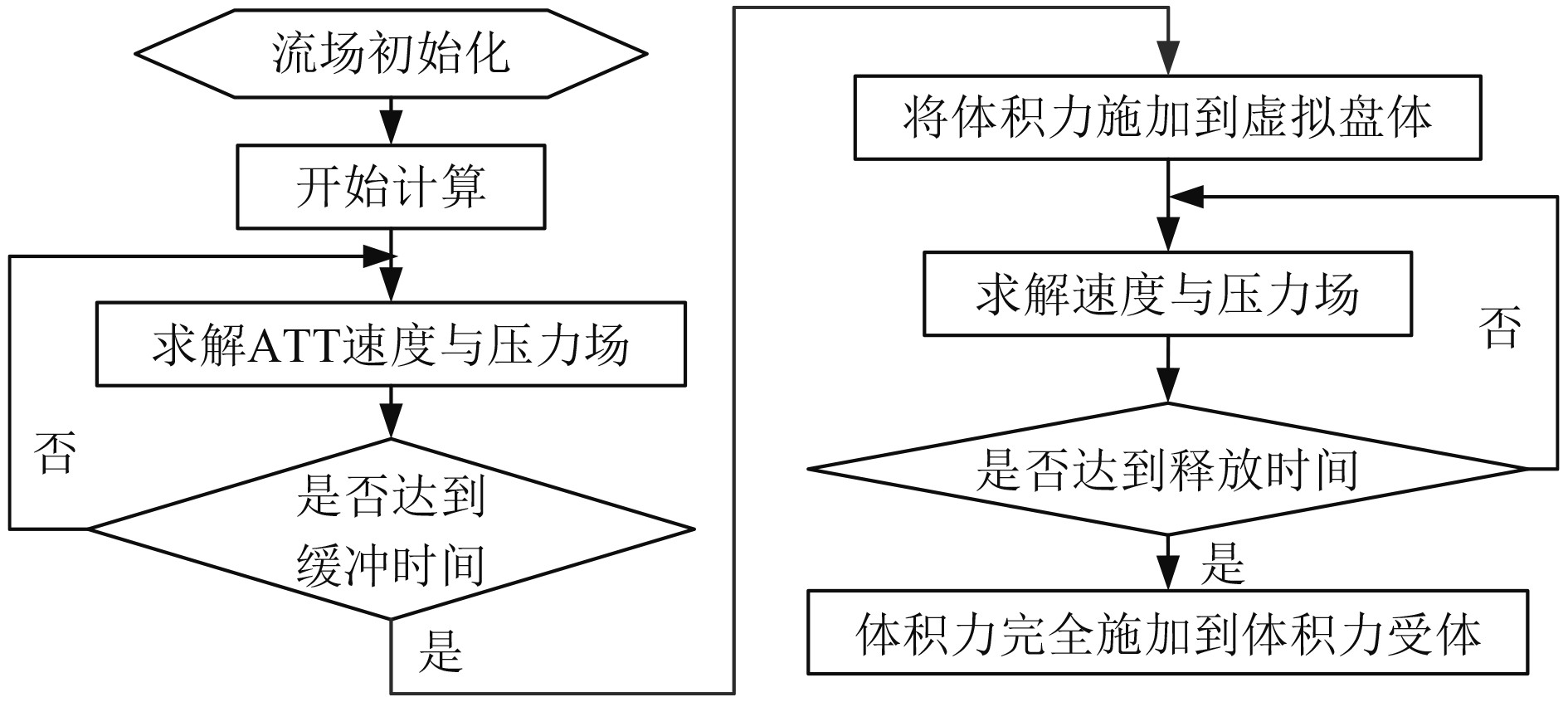
体积力虚拟盘计算流程如图6所示。
|
图 6 虚拟盘求解流程 Fig. 6 Virtual disk solution process |
对推进器缩比模型进行拖曳试验,试验过程中保持推进器的转速相同,监测不同进速系数下推进器的推力系数、扭矩系数并计算推进效率。
真实叶片几何和替代方案仿真时,均采用k-ω法进行求解,虚拟盘体速度入口、压力出口以及壁面采用和真实叶片几何数值模拟时相同的参数,转速恒定为7 r/min。监视推进器总推力时选取部件为转子,定子及导管;监视转矩时部件选择转子。仿真结果和实验结果如表1所示。
|
|
表 1 数值模拟结果和试验结果 Tab.1 Numerical simulation results and test results |
表1的推力系数、转矩系数和推进效率是相对于包括了导管,轮毂、后导流帽、叶片几何(虚拟盘)后的总推力系数、转矩系数、总效率。其中Exp 、VD_CFD、CFD分别表示实验结果、虚拟盘替代叶片仿真结果以及真实叶片几何仿真结果。
推进效率的数值模拟结果和试验结果对比如图7所示。

|
图 7 推进器效率数值模拟结果和试验结果 Fig. 7 Numerical simulation and experimental results of propeller efficiency |
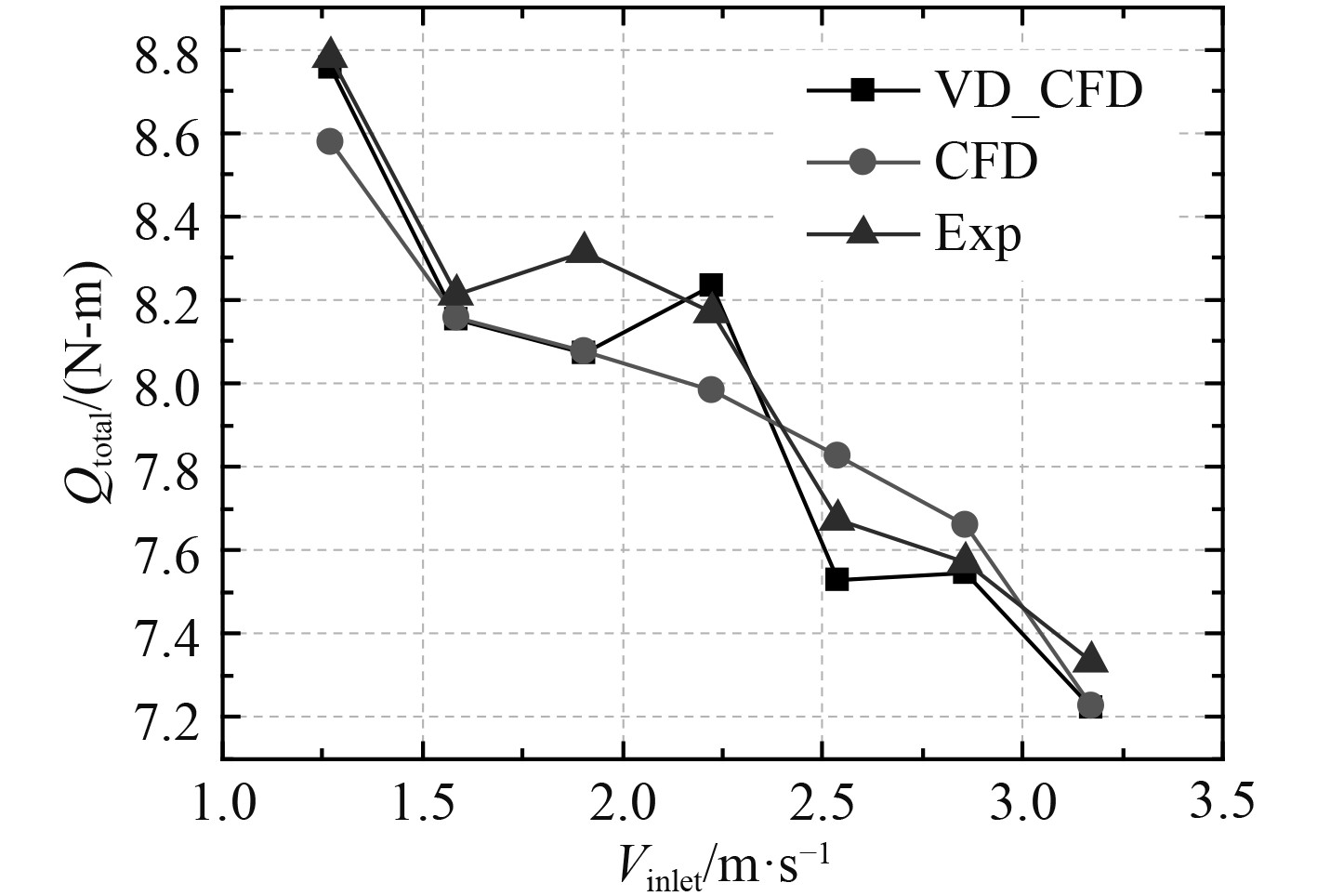
实际推进器导管、转子、定子所受的推力和力矩与替代方案导管、转子、定子受力如图8所示,所受力矩如图9所示。

|
图 8 实际推进器总推力与替代方案对比图 Fig. 8 Comparison between actual total thrust of thrusters and alternative solutions |
|
图 9 实际推进器总转矩与替代方案对比图 Fig. 9 Comparison between actual total torque of thrusters and alternative solutions |
从表1可知,采用数值模拟预报真实推进器几何的推进能力具有较高的精度,当给定虚拟盘体的工作条件以及工作点时,虚拟盘体产生的推力和设推力基本相等,虚拟盘和推进导管以及轮毂相互作用下虚拟盘、导管以及轮毂产生的总推力和转矩和真实叶片几何模拟时产生的推力和转矩基本相等且替代方案的推进效率和真实推进器的效率很接近,相对误差在5%以内。
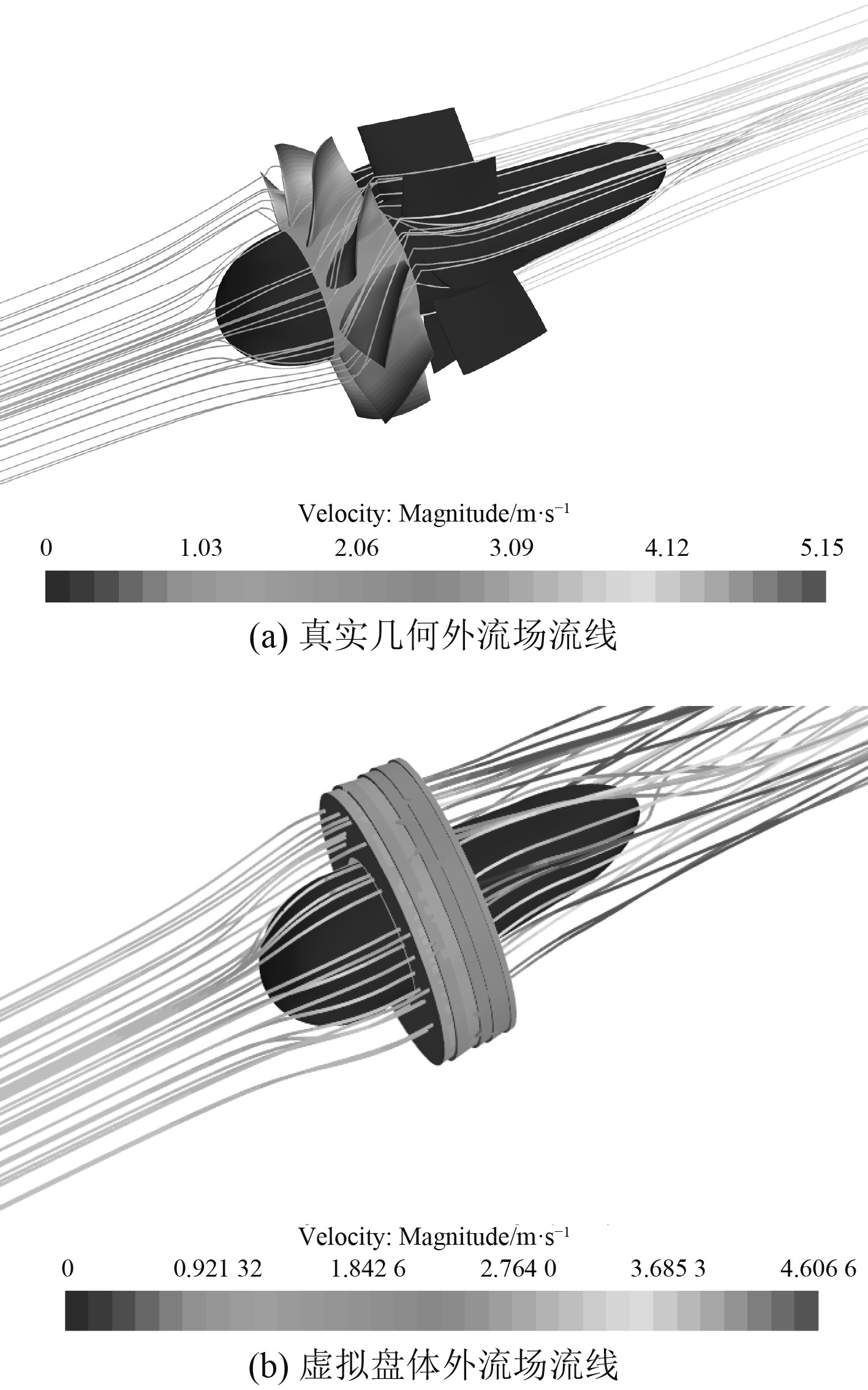
3.4 替代方案的推进器外流场与真实叶片几何流场分析为了分析替代方案的推进器外流场和真实叶片几何的外流场,对速度场和流线进行分析,仿真结果如图10和图11所示,图中速度场和流线为真实叶片几何进速系数为2和替代方案进速系数为2.1588时的求解结果。

|
图 10 叶片几何和虚拟盘体速度场分布图 Fig. 10 Velocity field distribution of blade geometry and virtual disk |
|
图 11 叶片几何和虚拟盘流线图 Fig. 11 Streamline diagram of blade geometry and virtual disk |
从图10可知,采用虚拟盘代替叶片几何时,推进器外流场较为相似,虚拟盘能较好模拟推进器外流场和内流场情况。
从图11可知,虚拟盘体和真实叶片几何模拟过程中,流经推进器的水流具有相似的诱导速度与流线分布,因此使用虚拟盘替代叶片几何时,能够简化舰船、潜艇以及水下航行器操纵性预报的计算开销,在没有完成适配推进器设计情况下快速相关分析。
4 结 语本文通过对某水下航行器泵喷推进器实际几何模型进行推进性能数值模拟,并采用体积力虚拟盘替代叶片真实几何,模拟体积力虚拟盘产生的推力和转矩与推进器工作时叶片几何产生等效推力和转矩时的推进器总体性能,对比分析虚拟盘体、真实叶片几何以及试验3种情况下推进器的总推力系数和转矩系数,结果表明在允许误差范围内,采用虚拟盘体代替叶片几何,能够产生和真实叶片几何近似等效的水力性能。
具体结论如下:
1)数值模拟方式对泵喷推进器推进性能进行模拟求解具有较高的求解精度,推力和转矩的预报误差均在6%以内,能够满足工程模拟的精度;
2)采用体积力虚拟盘体代替叶片几何进行推进器推进能力模拟时,采用等价变换的方式求解体积力虚拟盘的敞水性能参数并作用于虚拟盘体具有较高的预报精度,虚拟盘体所能产生虚拟盘体推力和预期推力基本相同;
3)虚拟盘替代叶片几何模拟泵喷推进器性能时,由于没有定子叶片,导管喷口水流速度相对于叶片几何的速度有所提高,但是虚拟盘推力、导管、轮毂以及后部导流帽产生的沿推进器轴向的力近似相等,总推力误差和转矩误差均能控制在5%以内,因此替代方案用于操纵性预报时具有较强的可行性。
| [1] |
吴浩, 欧勇鹏, 向国. 体积力法在船舶自由直航数值计算中的影响因素研究[J]. 武汉理工大学学报(交通科学与工程版), 2017, 41(2): 273-276. WU H, OU Y P, XIANG Guo. Research on the influencing factors of body force method in numerical simulation of ship self-propulsion[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2017, 41(2): 273-276. |
| [2] |
庄丽帆, 王志东, 凌宏杰, 等. 大型集装箱船船桨舵干扰特性数值模拟与分析[J]. 江苏科技大学学报(自然科学版), 2016, 30(6): 206-212. ZHUANG L F, WANG Z D, LING H J, et al. Numerical simulation and analysis of the interference characteristics between hull and propeller and rudder of an ultra-large container ship[J]. Journal of Jiangsu University of Science and Technology ( Natural Science Edition), 2016, 30(6): 206-212. |
| [3] |
沈海龙, 苏玉民. 基于滑移网格技术的船桨相互干扰研究[J]. 哈尔滨工程大学学报, 2010, 31(1): 1-7. SHEN H L, SU Y M. Use of the sliding mesh technique to analyze interaction between ship hulls and propellers[J]. Journal of Harbin Engineering University, 2010, 31(1): 1-7. DOI:10.3969/j.issn.1006-7043.2010.01.001 |
| [4] |
BEKHIT A S. Numerical simulation of the ship self propulsion prediction using body force method and fully discretized propeller model[C]//IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2018, 400(4): 042004.
|
| [5] |
张建武, 王志鹏, 胡科. 基于数值计算的某油轮快速性虚拟试验研究[J]. 中国造船, 2019, 60(1): 22-29. ZHANG J W, WANG Z P, HU Ke. Research on virtual test of powering performance for a tanker based on numerical calculation[J]. Shipbuilding of China, 2019, 60(1): 22-29. DOI:10.3969/j.issn.1000-4882.2019.01.003 |
| [6] |
王慧婷, 毕毅. 基于体积力法的全附体 KCS型船模 PMM运动数值模拟[J]. 中国舰船研究, 2016, 11(4): 29-37,66. WANG H T, BI Y. Numerical simulation on planar motion mechanism of KCS ship model with a body-force propeller model[J]. Chinese Journal of Ship Research, 2016, 11(4): 29-37,66. |
| [7] |
CAI B, MAO X, XU Q, et al. Simulation of the interaction between ship and ducted propeller with a modified body force method[J]. Ocean Engineering, 2022, 249: 110950. DOI:10.1016/j.oceaneng.2022.110950 |
| [8] |
吴召华, 陈作钢, 代燚. 基于体积力法的船体自航性能数值预报[J]. 上海交通大学学报, 2013, 47(6): 943-949. WU Z H, CHEN Z G, DAI Yi. Mumerical prediction of self-propulsion with a body -force propeller model[J]. Journal of Shanghai Jiao Tong University, 2013, 47(6): 943-949. DOI:10.16183/j.cnki.jsjtu.2013.06.018 |
| [9] |
魏可可, 高霄鹏. 基于体积力模型的潜艇应急上浮运动数值模拟分析[J]. 中国舰船研究, 2021, 16(2): 49–56. WEI K K, GAO X P. Numerical simulation of emergency surfacing motion of submarine based on volumetric force model[ J]. Chinese Journal of Ship Research, 2021, 16(2): 49–56. |
| [10] |
傅慧萍, THAD J M, PABLO M C. 一种基于体积力螺旋桨模型的自航计算方法[J]. 船舶力学, 2015, 19(7): 791-796. FU H P, THAD J M, PABLO M C. Computation on self-propulsion at ship point based on a body-force propeller[J]. Journal of Ship Mechanics, 2015, 19(7): 791-796. DOI:10.3969/j.issn.1007-7294.2015.07.005 |
| [11] |
王明哲, 王建华, 万德成. 用螺旋桨体积力模型数值模拟船舶自航[C]//第十六届全国水动力学学术会议暨第三十二届全国水动力学研讨会论文集(下册), 2021: 776–785. WANG M Z, WANG J H, WAN D C. Numerical solution of self-propulsion test with propeller body-force modle[C]//Proceedings of the 16th National Congress on Hydrodynamics & the 32nd national Conference on Hydrodynamics (Volume II) , 2021: 776–785. |
| [12] |
鹿麟. 泵喷推进器设计与流场特性研究[D]. 西安: 西北工业大学, 2016.
|
| [13] |
WANG C, WENG K Q, GUO C Y. Prediction of hydrodynamic performance of pump propeller considering the effect of tip vortex [J]. Ocean Engineering, 2019: 171, 259–272.
|
| [14] |
操戈, 余嘉威, 冯大奎, 等. 基于体积力方法的船舶波浪回转运动数值仿真[J]. 舰船科学技术, 2022, 44(01): 39-45. CAO G, YU J W, FENG Dakui, et al. Numerical simulation of ship turning in wave based on body-force method[J]. Ship Science and Technology, 2022, 44(01): 39-45. DOI:10.3404/j.issn.1672-7649.2022.01.008 |
| [15] |
何涛, 冯大奎, 张航, 等. 基于改进体积力方法的实尺度船舶回转运动数值仿真[J]. 中国造船, 2020, 61(S2): 52-63. HE T, FENG D K, ZHANG H, et al. Numerical simulation of full-scale ship turning motion[J]. Shipbuilding of China, 2020, 61(S2): 52-63. |
 2023, Vol. 45
2023, Vol. 45
