2. 中南大学 交通运输工程学院 轨道交通安全教育部重点实验室,湖南 长沙 410075
2. Key Laboratory of Traffic Safety on Track, Ministry of Education, School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China
涡激振动是指流体以一定流速流经钝体时产生漩涡而反作用于钝体,使其发生周期性振动的自然现象。涡激振动现象广泛存在于工程实际中,如海洋立管在一定流速的风或海洋中均存在涡激振动现象,设计时考虑不当可能导致结构受到涡激振动力而严重破坏,造成巨大损失。因此,涡激振动是海洋工程等学科关注较高的一个问题。
最简单的涡激振动现象就是单圆柱的涡激振动,国内外学者对此已有大量研究,并获得了较为成熟的成果[1-2]。许多参数都在一定程度上对圆柱涡激振动响应有所影响。m*作为振动圆柱的结构参数,其变化带来的影响较为显著。有许多学者[3-5]将m*ζ作为影响圆柱振动的参数进行研究。Griffin[6]将大量研究结果整合,列出了圆柱振幅和以m*ζ为变量的参数SG的曲线,即Griffin曲线[7]。Griffin曲线被广泛应用于海洋工程中立管涡激振动的预测。Khalak等[8]通过实验探究了m*ζ对圆柱涡激振动的影响,发现在低m*ζ下,圆柱响应模式分为初始分支、上分支和下分支,而在高m*ζ下,仅有初始分支和下分支。谷家扬[9]等采用有限体积法模拟了质量比在2~5之间变化下圆柱涡激振动响应,发现质量比越大,振动锁频区域越小。
当圆柱不再是单个时,剪切层、涡以及结构之间存在非常复杂的相互作用。双圆柱是研究多圆柱的基础模型。Assi等[10]通过实验重点关注了串列圆柱中下游圆柱的振动响应,并观察到了发散的驰振现象。Qin等[11]通过实验研究了2个串列圆柱在L/D = 0.7-5.5范围内的自由振动,并根据驰振产生机理和特征,基于L/D给出了4个不同的振动区域。及春宁等[12]通过数值模拟在Re=100,m*=2的条件下对串列双圆柱的涡激振动及其耦合机制进行了分析,其结果表明,无论上游圆柱固定与否,下游圆柱振幅和受力均大于单圆柱。陈威霖等[13]在Re=100的情况下对小间距比(L*=1.1~1.5)下串列双圆柱涡激振动进行了数值模拟研究,根据结果提出串列双圆柱涡激振动振幅在小间距比下要略小于大间距比,圆柱最大响应随间距的增加而增加。
目前对单圆柱及串列等直径双圆柱在低雷诺数下涡激振动的研究已取得了较多的成果,而不等直径圆柱涡激振动的研究还有待进一步发展。此外,对于参数m*ζ在涡激振动的影响也已有一些研究,但是对m*或ζ单个参数变化对圆柱响应影响的研究还较少,尤其是m*在较大范围内变化时圆柱振幅、受力情况的变化。为此,本文通过数值模拟对目前关注较少的质量比m*和阻尼比ζ单个参数变化对不同工况下圆柱涡激振动及受力的影响进行研究,工况选择单圆柱及不等直径串列双圆柱(上游小圆柱固定,下游圆柱弹性固定),为进一步探究不等直径双圆柱在中高雷诺数下涡激振动特性探究做准备。此外,还将利用计算结果探寻m*和ζ影响涡激振动的联系,验证将组合参数m*ζ作为研究涡激振动的变量的合理性。
1 模拟模型的建立基于拉格朗日-欧拉方法的不可压缩粘性流体,质量守恒方程(连续性方程)和动量守恒方程(N-S方程)表示如下:
| $ \frac{\partial \overrightarrow{\rho }}{\partial t}+\nabla \cdot \left(\overrightarrow{\rho }\overrightarrow{v}\right)=0,$ | (1) |
| $ \frac{\partial \left(\overrightarrow{\rho }\overrightarrow{v}\right)}{\partial t}+\left(\overrightarrow{\rho }\overrightarrow{v}\cdot \nabla \right)\overrightarrow{v}=\overrightarrow{\rho }\overrightarrow{f}-\nabla \overrightarrow{p}-\mu {\nabla }^{2}\overrightarrow{v}。$ | (2) |
式中:
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0 ,$ | (3) |
| $ \left\{ \begin{gathered} \rho \left( {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}}} \right) = - \frac{{\partial p}}{{\partial x}} + \mu \left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}}} \right) ,\\ \rho \left( {\frac{{\partial v}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}}} \right) = - \frac{{\partial p}}{{\partial x}} + \mu \left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}}} \right) 。\\ \end{gathered} \right. $ | (4) |
式中:
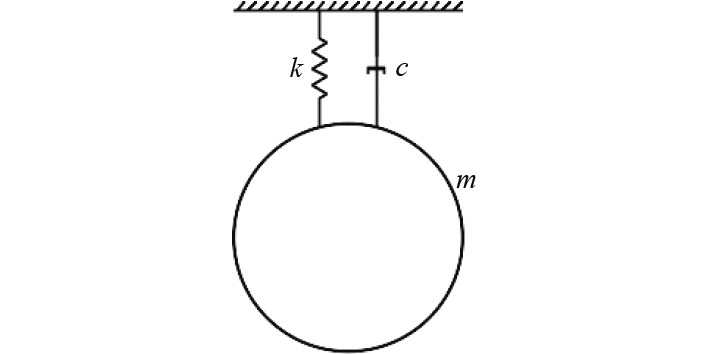
振动圆柱视为刚体,固定方式为单自由度弹性固定,可在横流向进行自由振动。对于在横流向作自由振动的大圆柱,可以看作为质量-弹簧-阻尼系统(见图1),其运动方程如下:
|
图 1 单自由度振动圆柱系统 Fig. 1 Single-degree of vibrating cylinder system |
| $ m\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} + c\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + ky = {F_L} 。$ | (5) |
式中:m*为圆柱振动质量;c为系统阻尼;k为弹簧刚度;y为圆柱横流向的位移;FL为圆柱所受升力。
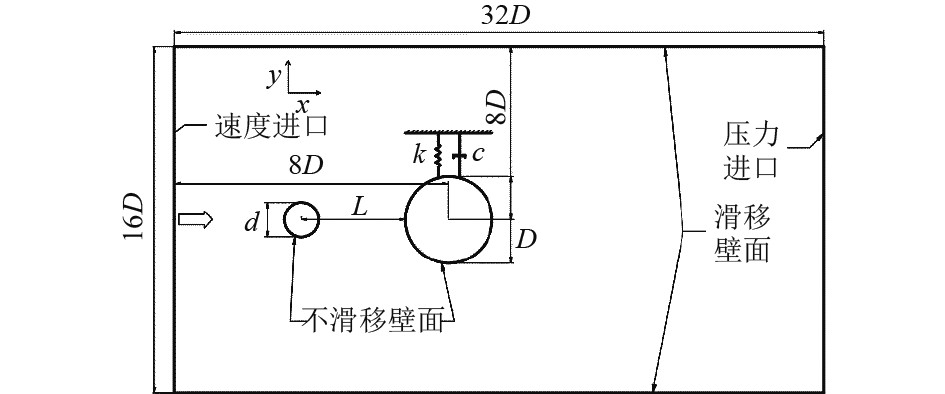
基于流体计算软件STAR-CCM+建立模拟模型,区域尺寸及边界设置如图2所示。固定圆柱直径为d,振动圆柱直径为D,流体区域流向尺寸为32D,横向尺寸为16D,振动圆柱与入口边界距离8D,与上下边界距离为8D。流体域入口边界设置为速度进口,流速v=U∞,出口设置为压力出口,出口压力p0=0 Pa,上下边界为滑移壁面,圆柱面设置为不滑移壁面。
|
图 2 计算区域和边界条件设置 Fig. 2 The setting of computational area and boundary conditions |
对于流体域的控制方程,采用有限体积法离散求解;圆柱的振动位移,采用动态流体相互作用模块(DFBI)进行求解。
圆柱与流体之间的耦合采用STAR-CCM+中重叠网格技术来实现。重叠网格是用来离散相互重叠的2个或多个不同网格的计算域,它在处理涉及多个体或移动体的问题时以及优化研究中具有优势。在重叠网格中,网格单元包括活动、不活动网格单元。在活动网格单元中,将对控制方程进行求解。而不活动网格单元仅会在重叠区域发生移动或者旋转等运动时,才会变为活动状态并进行方程求解[14]。受体网格单元是分离活动和不活动网格的边界,其与重叠网格的边界相连接,其作用为耦合重叠与非重叠区域控制方程的求解。供体网格通过插值方法为受体网格单元提供数据信息。
在本文中,流体域为主要网格,结构域为次要网格,两区域均采用四面体网格(见图3),靠近圆柱的部位网格加密而远离圆柱的部位网格稀疏。主要网格固定在空间中,而次要网格可以静止或移动。主次要网格间的耦合连接需要重叠边界处的受体网格找到提供信息的供体网格单元。选择加权距离插值方法,即插值因子与供体与受体间距离成反比,距离越近的供体网格单元影响越大。

|
图 3 计算区域网格划分 Fig. 3 The mesh of computational area |
为了验证本文数值模拟方法的正确性,分别对固定单圆柱绕流和单圆柱涡激振动进行计算,并与文献结果进行对比。
2.1 固定单圆柱绕流对Re=100的固定单圆柱绕流采用上述数值模拟方法进行仿真,将计算所得阻力系数平均值CD,升力系数均方根值CLrms,斯特劳哈尔数St与已有文献中数值模拟值和实验值进行对比,结果如表1所示。可以看出,本文结果与文献吻合较好。
|
|
表 1 固定单圆柱绕流结果对比 Tab.1 The comparison of flow past a single fixed cylinder |
选取Shiels[20]等的4组数值模拟(见表2)结果对单圆柱涡激振动进行对比,结果如表3所示。由计算结果可知,各组参数均与Shiels等的结果匹配较好。
|
|
表 2 单圆柱涡激振动验证参数设置 Tab.2 The parameter setting of single cylinder vortex-induced vibration |
|
|
表 3 单圆柱涡激振动计算结果对比 Tab.3 The comparison of single cylinder vortex-induced vibration |
由以上固定圆柱绕流和涡激振动的对比结果可知,本文计算方法与模型具有良好的计算精度与可靠性。
3 模拟结果分析与讨论对单自由度圆柱、与固定小圆柱串列的单自由度圆柱涡激振动进行数值模拟,探究质量比m*及阻尼比ζ对不同工况下单自由度圆柱涡激振动以及流体力的影响,并将2组计算结果进行对比,得出两参数对圆柱涡激振动影响的联系。模拟工况设置如表4所示。
|
|
表 4 计算工况 Tab.4 The simulation condition |
模拟基本参数设置:基于振动圆柱直径的雷诺数Re=ρU∞D/μ,其中ρ为流体密度,U∞为自然来流速度,D为振动圆柱的直径,μ为流体动力粘度;约化速度Ur=U∞/fnD,其中
对于圆柱振动响应,采用最大相对振幅A*max描述,其定义为A*max=Ymax /D。式中,Ymax为圆柱最大横向振幅。对于流体力,采用升力系数均方根值CLrms和阻力系数平均值CD来描述。其中,
对4种工况在固定阻尼比ζ=0.1,质量比m*在1~300的范围内改变进行数值模拟。
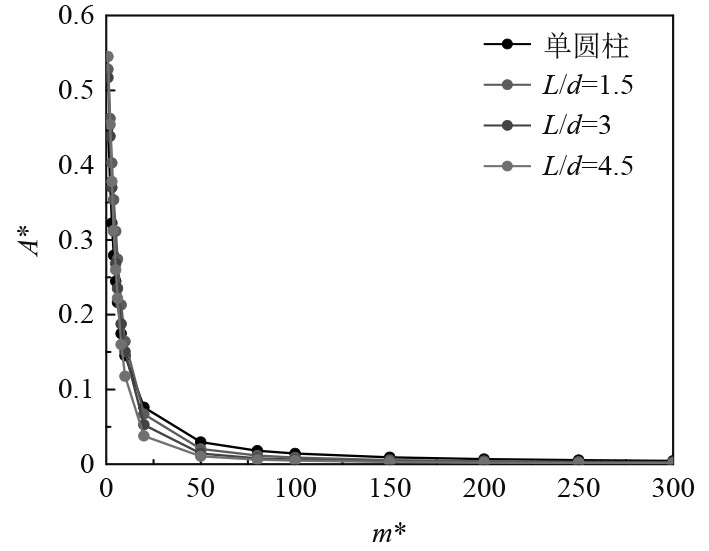
振动圆柱最大相对振幅A*max与质量比m*关系如图4所示。m*<20时,圆柱振幅受质量比变化影响较大,随着质量比的增加,最大振幅迅速下降。在m*≥20时,各工况圆柱最大相对振幅均低于0.1,振动较小,且在m*≥100后振动几乎可以忽略不计。计算中采用的约化速度UR=5在低质量比下(m*<5)处在锁定区域[21]。潘志远等[2, 22-23]认为,质量比m*在O(100)量级上时,锁定频率约等于结构固有频率,而在O(1)量级时,锁定区域宽度显著增加,且m*越小,锁定区域上限频率越高。图4中,圆柱振幅随质量比变化情况从另一个角度反映出锁定区域变小的现象。
|
图 4 各工况圆柱相对振幅随质量比(m*=1~300)变化 Fig. 4 Variations of dimensionless oscillating amplitude with mass ratio (m*=1~300) |
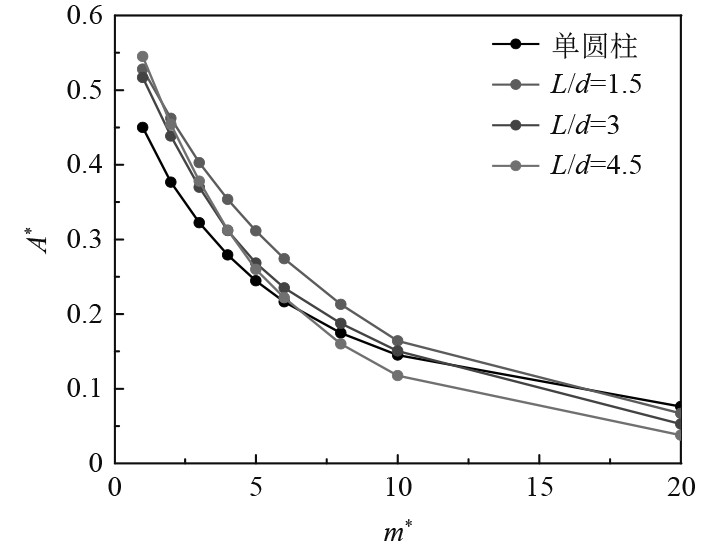
图5为m*=1~20时各工况圆柱振幅变化。在m*=1时,与固定小圆柱串列的圆柱在间距比L/d=4.5的工况下振幅是最大的,而随着质量比的增加,该工况圆柱振幅迅速降低,在m*>6后振幅为4个工况中最小。整体来看,与固定小圆柱串列的圆柱在m*较小时,振动相对单圆柱时有所增强,但是受质量比变化影响较大。分析认为,与固定小圆柱串列的圆柱振动除了受来流作用,还受到固定小圆柱尾涡的影响(在小间距时(L/d<3),小圆柱尾涡未完全产生便附着作用于振动圆柱,使其产生振动;而在大间距时(L/d=4.5),小圆柱尾涡完全产生,与流体共同作用于振动圆柱使其产生振动。但是上游小圆柱产生的尾涡作用相比稳定的来流,受振动圆柱质量比影响较大,这也解释了单圆柱在较高质量比时振幅高于与固定小圆柱串列的现象。
|
图 5 各工况圆柱相对振幅随质量比(m*=1~20)变化 Fig. 5 Variations of dimensionless oscillating amplitude with mass ratio (m*=1~20) |
各工况的部分涡量图(m*=1,5,10,20,50,100,200,300)如图6~图9所示。在低质量比时,串列工况下尾涡迅速变为两列平行涡脱落,单圆柱则在脱落多个周期后才逐渐形成两列平行涡。随着质量比的增加,形成平行涡模式的时间越来越长,当质量比增加至50时,各工况尾涡几乎不再形成两列涡,而是以单列涡形式进行脱落。

|
图 6 单圆柱涡量图(m*=1,5,10,20,50,100,200,300) Fig. 6 The vorticity contours of Single cylinder(m*=1,5,10,20,50,100,200,300) |

|
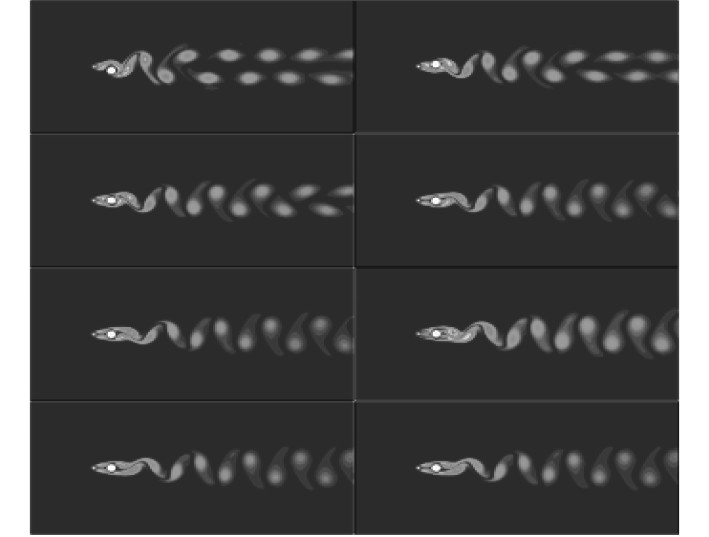
图 7 L/d=3涡量图(m*=1,5,10,20,50,100,200,300) Fig. 7 The vorticity contours of tandem cylinders with L/d=1.5(m*=1,5,10,20,50,100,200,300) |
|
图 8 L/d=4.5涡量图(m*=1,5,10,20,50,100,200,300) Fig. 8 The vorticity contours of tandem cylinders with L/d=3(m*=1,5,10,20,50,100,200,300) |

|
图 9 L/d=4.5涡量图(m*=1,5,10,20,50,100,200,300) Fig. 9 The vorticity contours of tandem cylinders with L/d=4.5(m*=1,5,10,20,50,100,200,300) |
振动圆柱所受升力系数和阻力系数与质量比m*关系如图10和图11所示。各工况下圆柱所受升力在低质量比(m*<8)时随质量比增加而迅速增加,随后逐渐下降,在m*>6后受力趋于稳定,基本不再随质量比变化而变化。在升力上升区间,串列工况下圆柱受力随间距的增加而减少,但均大于单圆柱情况。L/d=4.5时升力拐点位于m*=6处,相比另2种串列工况m*=8的拐点较为提前。在稳定区间,单圆柱所受升力远大于串列工况下各圆柱。升力与横向振动直接相关,因此其变化机理也与振动类似,在低质量比时,串列工况下,振动圆柱受小圆柱尾涡作用,使其受力高于单圆柱。随着质量比的升高,尾涡作用相比稳定来流受质量比变化影响更大,因此单圆柱受力随质量比的增加而逐渐大于串列工况各圆柱。

|
图 10 各工况圆柱升力系数均方根随阻尼比(m*=1~20)变化 Fig. 10 Variations of RMS value of lift coefficient with mass ratio (m*=1~300) |

|
图 11 各工况圆柱阻力系数平均值随阻尼比(m*=1~20)变化 Fig. 11 Variations of average drag coefficient with mass ratio (m*=1~300) |
各工况圆柱所受阻力在m*<20时呈下降趋势,在m*>20后趋于平稳。单圆柱所受阻力在高质量比时远大于串列工况,而在较低质量比情况下受力相差较小。串列工况中,各圆柱受阻力随间距的增大而减小。由于上游固定小圆柱的阻流作用,串列工况下的阻力相比单圆柱更低。
3.2 变阻尼比下圆柱涡激振动对工况1和工况2在固定质量比m*=1,阻尼比ζ在0~1范围内改变的圆柱涡激振动及受力情况进行数值模拟。
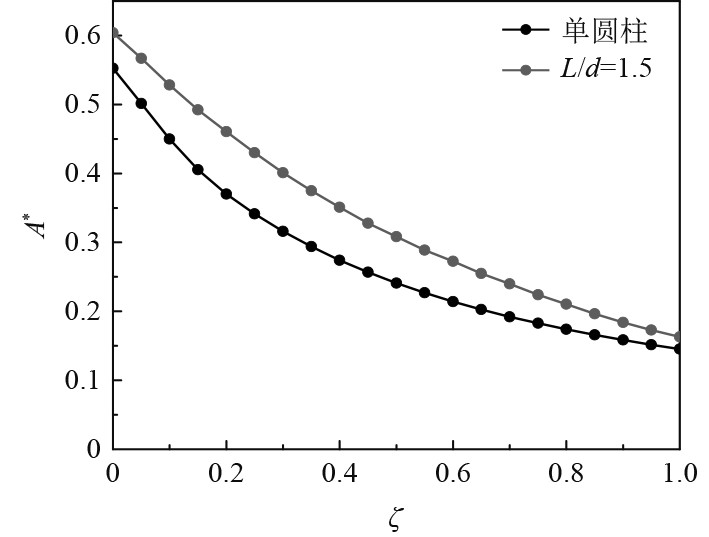
振动圆柱的振幅随阻尼比变化的曲线如图12所示。在ζ=0~1内,圆柱振幅随阻尼比的增大而减小,串列工况下圆柱振幅高于单圆柱。在ζ=0.2~0.4时串列工况圆柱振幅与单圆柱相比差距较大,而在ζ接近1时,两者振幅趋近于相等。各工况部分涡量图如图13和图14所示(ζ=0,0.2,0.4,0.6,0.8,1.0)。与质量比影响下类似,ζ较小,振幅较大时,圆柱尾涡脱落快速形成两列平行涡,而随着ζ增加,尾涡形成平行涡的速度变慢,以单列涡形式进行脱落。
|
图 12 各工况圆柱相对振幅随阻尼比(ζ=0~1)变化 Fig. 12 Variations of dimensionless oscillating amplitude with damping ratio (ζ=0~1) |

|
图 13 单圆柱涡量图(ζ=0,0.2,0.4,0.6,0.8,1) Fig. 13 The vorticity contours of single cylinder (ζ=0,0.2,0.4,0.6,0.8,1) |

|
图 14 L/d=1.5涡量图(ζ=0,0.2,0.4,0.6,0.8,1) Fig. 14 The vorticity contours of tandem cylinders with L/d=1.5(ζ=0,0.2,0.4,0.6,0.8,1) |
圆柱所受升力系数和阻力系数随阻尼比变化的曲线如图15和图16所示。随着阻尼比的增加,圆柱所受升力逐渐增大。串列工况下圆柱所受升力整体高于单圆柱,在ζ=0.2后串列圆柱所受升力增量大于单圆柱,在ζ=0.8之后两者升力又趋于相等。阻力则随阻尼比的增加而减小,单圆柱所受阻力较串列工况下略大,且减小相对平缓。

|
图 15 各工况圆柱升力系数均方根随质量比(ζ=0~1)变化 Fig. 15 Variations of RMS value of lift coefficient with damping ratio (ζ=0~1) |

|
图 16 各工况圆柱阻力系数平均值随阻尼比(ζ=0~1)变化 Fig. 16 Variations of average drag coefficient with mass ratio (ζ=0~1) |
现有部分文献将参数m*ζ作为整体来探究其对圆柱涡激振动的影响,本文利用工况1和工况2的模拟结果验证其合理性。
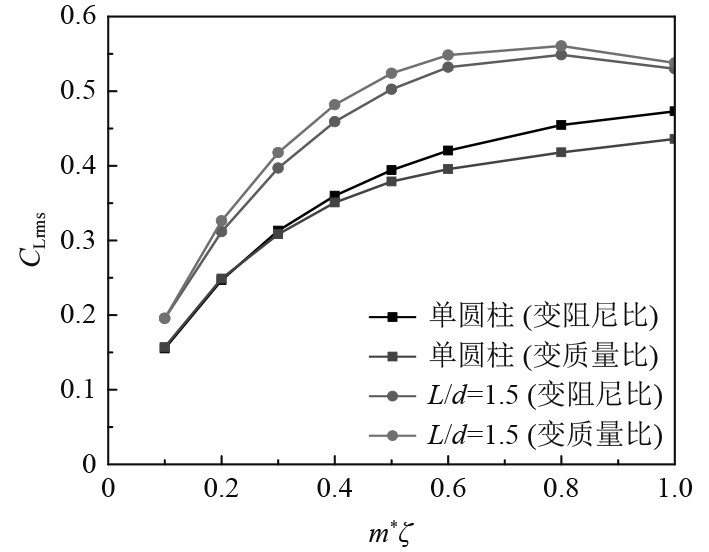
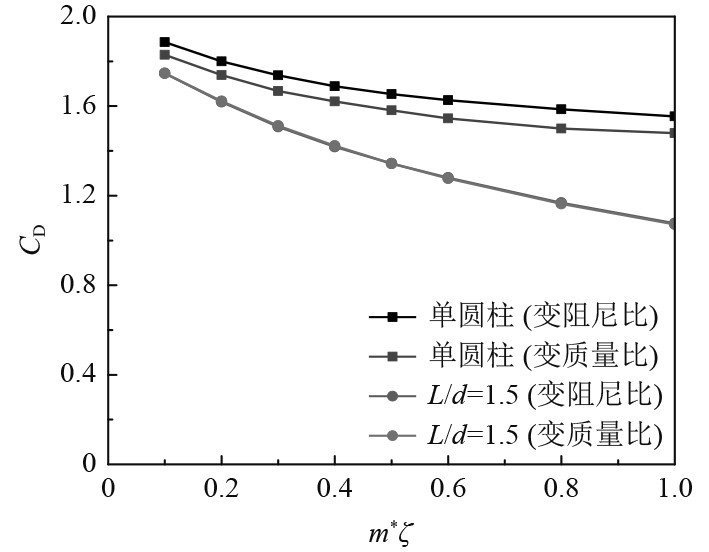
如图17~图19所示,2种工况在m*ζ相等而分别改变质量比和阻尼比时,圆柱最大振幅几乎完全相等。升力系数和阻力系数整体吻合度均较高,但是单圆柱的升力系数在m*ζ>0.4时变阻尼比和变质量比情况下升力曲线呈分离趋势,最大差值不足0.05;阻力系数则在整个区间上均有一定的差异,但差值也不足0.1。串列工况下振幅和阻力系数几乎完全吻合,而升力系数最大差值也不足0.05。其中单圆柱振幅随m*ζ变化曲线与Griffin曲线[7]吻合较好。因此,在对低雷诺数圆柱涡激振动响应的分析或实验中,以m*ζ作为组合参数来控制是合理的。

|
图 17 各工况圆柱相对振幅随质量-阻尼比(m*ζ=0.1~1)变化 Fig. 17 Variations of dimensionless oscillating amplitude with mass-damping ratio (m*ζ=0.1~1) |
|
图 18 各工况圆柱升力系数均方根随质量-阻尼比(m*ζ=0.1~1)变化 Fig. 18 Variations of RMS value of lift coefficient with mass-damping ratio (m*ζ=0.1~1) |
|
图 19 各工况圆柱阻力系数平均值随质量-阻尼比(m*ζ=0.1~1)变化 Fig. 19 Variations of average drag coefficient with mass-damping ratio (m*ζ=0.1~1) |
对Re=150的单自由度单圆柱及与固定小圆柱串列的圆柱涡激振动进行数值模拟,探究质量比m*(1~300)与阻尼比ξ(0~1)对圆柱振幅及受力的影响,得出如下结论:
1)保持ξ不变,当m*<20时,圆柱横向振幅和阻力随m*的增加而降低,升力则随之增大;当m*>20时,各参数逐渐趋于稳定,几乎不再随m*变化而变化,且圆柱相对振幅低于0.1,可以认为,随着质量比的增加,流固耦合作用变弱。相比与固定小圆柱串列的圆柱,单圆柱所受阻力较大,而振幅和升力在低质量比时较小,高质量比时较大。这是因为串列工况下,顺流方向上游圆柱对下游振动圆柱有了一定的阻流作用。在横流向,串列工况下振动圆柱受到上游固定小圆柱尾流的影响,在低质量比时比单圆柱有更高的振幅和升力。随着质量比的提高,尾流作用受影响相比稳定来流更大,单圆柱振幅和升力逐渐高于串列工况。
2)保持m*不变,圆柱横向振幅和阻力随ξ的增加而减小,其中与固定小圆柱串列的圆柱减小速率较快;升力随ξ的增加而增大。
3)各工况尾涡在低质量比或低阻尼比脱落时很快形成两列平行涡,随着质量比和阻尼比的提高,尾涡形成两列涡的速度减缓,当两参数提高到一定值时,尾涡不再形成两列涡,而是保持单列进行脱落。与固定小圆柱串列的圆柱相比单圆柱更容易形成两列涡。
4)在低雷诺数、m*ζ=0.1~1情况下,保持m*ζ值不变,m*和ξ不同时,圆柱横向振幅相同,受力大小也近似相等。相较现有文献仅给出圆柱振幅与m*ζ关系,本文补充了升力系数与阻力系数随m*ζ变化的情况,对低雷诺数下以m*ζ值为控制变量来进行实验研究提供更可靠的参考。
以上结论仅由低雷诺数层流的数值模拟中得到,而在中高雷诺数下是否有同样结论还有待进一步验证。
| [1] |
WILLIAMSON C H K. Vortex-induced vibration[J]. Annual Review of Fluid Mechanics, 2004, 36(1): 42. |
| [2] |
及春宁, 等. 圆柱涡激振动研究进展与展望[J]. 海洋技术学报, 2015, 34(1): 13. |
| [3] |
SCRUTON C. On the wind-excited oscillation of stacks, towers and masts [J]. Procconfon Wind Effects on Buildings & Structures, 1965.
|
| [4] |
SKOP R A, GRIFFIN O M. An heuristic model for determining flow-induced vibration of offshore structure [J]. Offshore Technology Conference, 1973
|
| [5] |
VICKERY B J, WATKINS R D. Flow-induced vibrations of cylindrical structures [M]. Richard Silvester, Hydraulics and Fluid Mechanics. Pergamon, 1964: 213–41.
|
| [6] |
GRIFFIN O M, SKOP R A, RAMBERG S E. The resonant vortex-excited vibrations of structures and cable systems [J]. Offshore Technology Conference 1975.
|
| [7] |
GRIFFIN O M. Vortex-excited cross-flow vibrations of a single cylindrical tube [J]. Journal of Pressure Vessel Technology, 1980, 102(2): 158–66.
|
| [8] |
KHALAK A, WILLIAMSON C. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping[J]. Journal of Fluids & Structures, 1999, 13(7-8): 813-51. |
| [9] |
谷家扬, 等. 质量比对圆柱涡激特性的影响研究 [J]. 振动与冲击, 2016, 35(4): 134–40.
|
| [10] |
RS G, ASSI, et al. Experimental investigation of flow-induced vibration interference between two circular cylinders [J]. Journal of Fluids and Structures, 2006.
|
| [11] |
QIN B, ALAM M M, ZHOU Y. Free vibrations of two tandem elastically mounted cylinders in crossflow[J]. Journal of Fluid Mechanics, 2019, 861: 349-81. DOI:10.1017/jfm.2018.913 |
| [12] |
及春宁, 等. 串列双圆柱流致振动的数值模拟及其耦合机制[J]. 力学学报, 2014, 46(6): 862-70. DOI:10.6052/0459-1879-14-118 |
| [13] |
陈威霖, 等. 小间距比下串列双圆柱涡激振动数值模拟研究: 振动响应和流体力[J]. 振动与冲击, 2018, 37(23): 9. |
| [14] |
白旭, 陈云. 串列不等直径双圆柱海流能发电振子涡激振动数值模拟[J]. 可再生能源, 2020, 38(12): 7. DOI:10.3969/j.issn.1671-5292.2020.12.021 |
| [15] |
PARK J, KWON K, CHOI H. Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160[J]. Ksme International Journal, 1998, 12(6): 1200-5. DOI:10.1007/BF02942594 |
| [16] |
陈威霖, 及春宁. 单圆柱涡激振动中的振幅不连续和相位切换现象研究[J]. 水动力学研究与进展:A辑, 2016(4): 8. |
| [17] |
STLBERG E, et al. High order accurate solution of flow past a circular cylinder[J]. Journal of Scientific Computing, 2006, 27(1): 431-41. |
| [18] |
WILLIAMSON C H K. Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers [J]. Journal of Fluid Mechanics, 1989, 206(1): 579–627.
|
| [19] |
TRITTON D J. , Experiments on the flow past a circular cylinder at low reynolds numbers[J]. Journal of Fluid Mechanics, 1959, 6(4): 547-67. DOI:10.1017/S0022112059000829 |
| [20] |
SHIELS D. , et al. Flow-induced vibration of a circular cylinder at limiting structural parameters [J]. Journal of Fluids & Structures, 2001.
|
| [21] |
韦昱呈, 鲁丽. 低雷诺数下圆柱顺流向和横流向涡激振动响应分析[J]. 四川轻化工大学学报:自然科学版, 2021, 34(5): 8. |
| [22] |
潘志远. 海洋立管涡激振动机理与预报方法研究 [D]. 上海: 上海交通大学, 2006.
|
| [23] |
潘志远, 等. 低质量-阻尼因子圆柱体的涡激振动预报模型[J]. 船舶力学, 2005, 9(5): 10. |
 2023, Vol. 45
2023, Vol. 45
