2. 武汉理工大学 航运学院,湖北 武汉 430063
2. School of Navigation, Wuhan University of Technology, Wuhan 430063, China
船舶运动模型是对船舶运动的动态系统特性的高度概括和理论抽象,反映了船舶在实际运动过程中的物理本质和变量的数量变化[1]。船舶运动模型是分析船舶操纵性、设计船舶操纵控制器、研发船舶操纵模拟器的关键[2]。王雪刚等[3-4]基于黑箱形式的船舶运动模型实现船舶操纵运动的预报;孙健等[5]使用船舶运动模型分析海浪中高速舰船的操纵性能。同时,随着船舶运动模型应用程度的逐渐加深,对其质量的要求也越来越高。
参数是船舶运动模型必不可少的组成部分,影响船舶运动模型的质量。实际中,船舶运动模型中大量的参数都是由船舶测量数据经过经验公式计算或者辨识得出的。基于试验数据的系统辨识是获取船舶运动模型参数的重要途径。杨诚[6]基于船舶运动仿真试验,提出一种基于自适应粒子群算法的船舶运动模型参数辨识优化方法;曹包华[7]基于自适应方法和遗忘因子最小二乘法对船舶模运动模型进行参数辨识,进而提出一种新型的船舶航向控制算法;毕革新[8]提出一种改进的Elman递归神经网络算法,对于船舶操纵运动的动态时变系统具有良好的辨识性能;李光磊等[9]结合最小二乘算法和间接模型参考自适应法,提出一种可有效应用于船舶操纵运动非线性系统的混合辨识算法。可见,参数辨识方法、辨识过程的操作性、辨识结果的精确度等,决定着船舶运动模型的质量[10]。合理有效的辨识方法及其工程应用性,对于船舶运动模型参数辨识具有重要意义。
为有效、准确估计实船操纵运动模型参数,本文基于系统辨识原理,提出一种采用递推最小二乘算法进行差分方程型船舶运动模型参数辨识的方法。基于试验操纵数据,将其应用于实船舵角-航向差分方程模型的参数辨识,以验证方法的有效性和参数辨识的准确性。
1 船舶及操纵试验 1.1 船舶及试验简介试验船舶选择“鄂石3199”油化品船。船总长90 m,最大宽度16.2 m,总吨2776 t,船舶主要参数如表1所示。试验地点选择为湖北省武汉市阳逻水道。该水道位于长江流域,上起王家屋,下至周阳港,全长约18 km,岸线平顺,地质结构稳定,不淤不滞,水深常年保持在7 m以上,试验当日阳逻水道流速1.0 m/s。
|
|
表 1 船舶主要参数 Tab.1 Main particulars of the concerned ship |
本文坐标系和参数的设置同文献[11-12],用以描述船舶运动。船舶运动系统输出是指各种状态变量的输出,如在固定坐标系
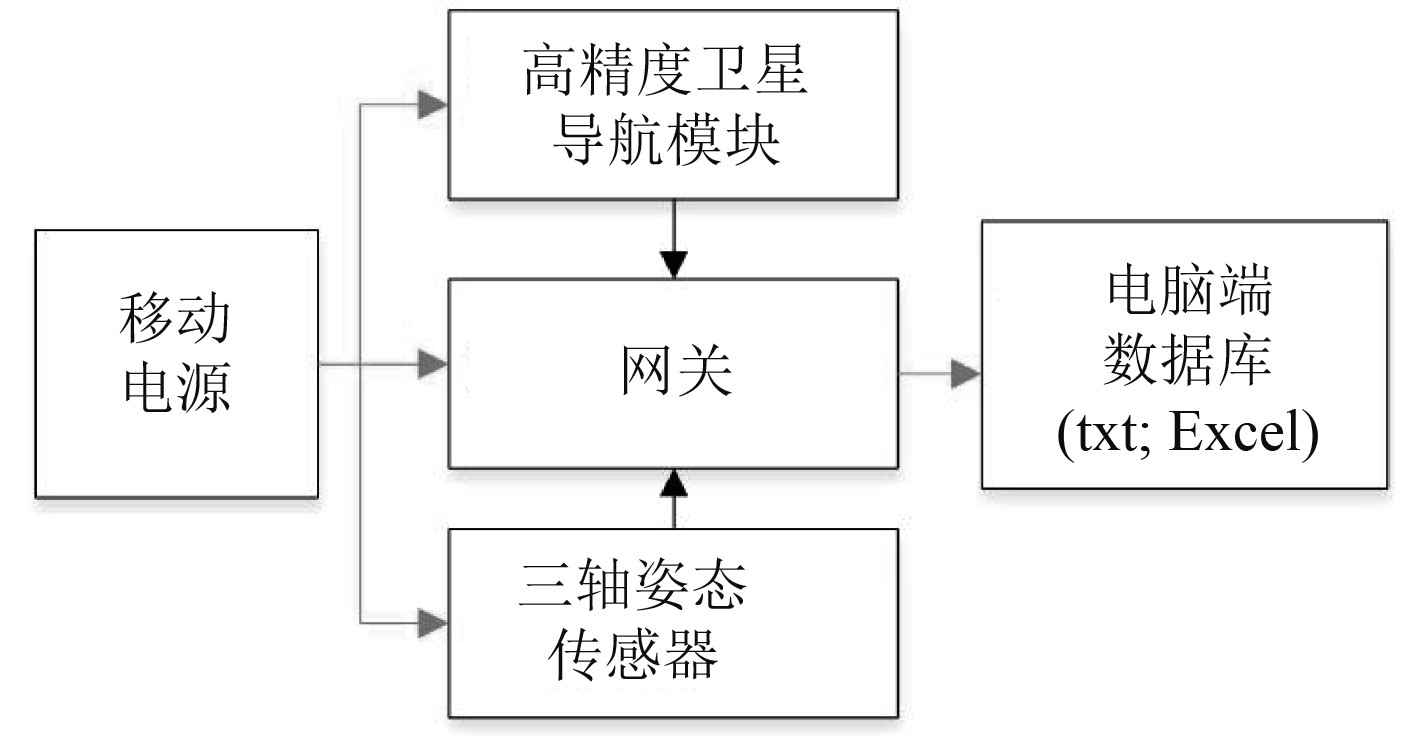
|
图 1 数据采集系统组成 Fig. 1 Structure of the data collection system |
整个试验过程的船舶运动航迹如图2所示。
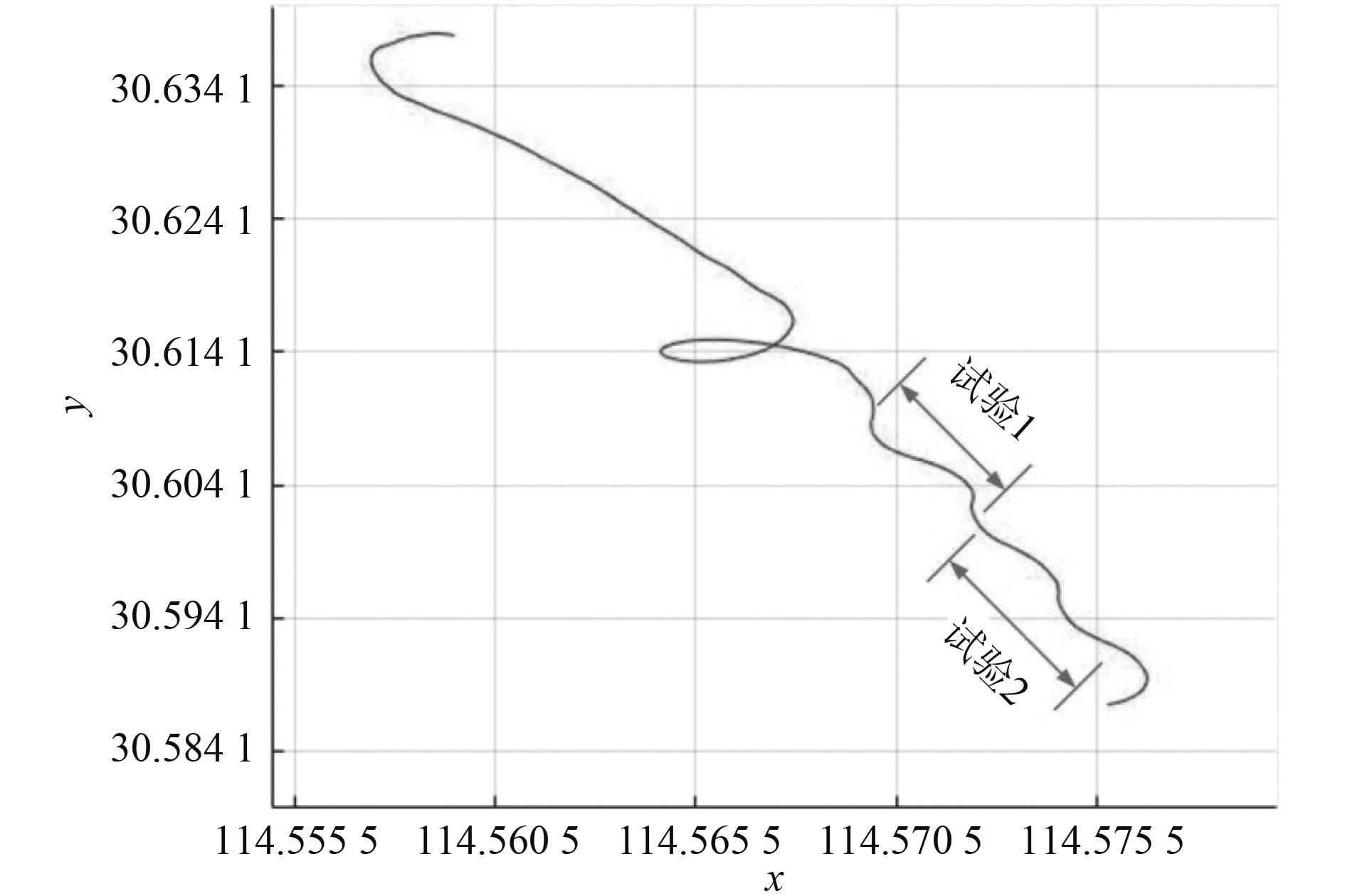
|
图 2 操纵试验全程航迹记录 Fig. 2 Ship track record during the whole journey of maneuvering test |
由图2可知,在整个试验过程中,系统输入-输出被相对较好的观测和记录的时间段共有2个,这2个时间段内所采集的数据质量较高,从而将试验1、试验2时段内的输入-输出作为本文数据来源。
由于某些情况下直接采集到的数据可能不适合直接使用,因此有必要采用合适的技术对原始数据进行预处理。本文数据预处理方式[11-12]有:1)异常数据替换,即采用移动平均方式对采样点上的空数据、明显异常数据予以替换;2)数据平均,即使用1 s时长内传感器所有采样点(约60个)数据的均值作为1 s结束后的瞬时采样值。就试验1、试验2时段内的数据进行预处理并画出,用于本文建模和参数辨识的系统输入-输出数据,如图3所示。其中,

|
图 3 两次Z型操纵试验的舵角—航向数据 Fig. 3 Data of rudder angle — heading corresponding to the two times of zigzag manouvering test |
取采样间隔为1 s,设
| $ \begin{aligned} &{r_{{k}}} = {\psi _{{{k + 1}}}} - {\psi _{{k}}} ,\\ & {{\dot r}_{{k}}} = {r_{{{k + 1}}}} - {r_{{k}}}= \\ & ({\psi _{{{k + 2}}}} - {\psi _{{{k + 1}}}}) - ({\psi _{{{k + 1}}}} - {\psi _{{k}}}) =\\ &{\psi _{{{k + 2}}}} - 2{\psi _{{{k + 1}}}} + {\psi _{{k}}} ,\\ \end{aligned} $ | (1) |
则对
| $ T({\psi }_{{k+2}}-2{\psi }_{{k+1}}+{\psi }_{{k}})+({\psi }_{{k+1}}-{\psi }_{{k}})=K{\delta }_{{k}},$ | (2) |
整理,得
| $ T{\psi _{{{k + 2}}}}{{ + }}\left( { - 2T + 1} \right){\psi _{{{k + 1}}}} + (T - 1){\psi _{{k}}}{{ = }}K{\delta _{{k}}} ,$ | (3) |
即
| $ {\psi _{{k}}}{\text{ + }}\frac{{ - 2T{\text{ + }}1}}{T}{\psi _{{{k + 1}}}} + \frac{{T - 1}}{T}{\psi _{{k}}}{\text{ = }}\frac{K}{T}{\delta _{{k}}} ,$ | (4) |
令:
| $ {\psi _{{{k + 2}}}}{\text{ + }}a{\psi _{{{k + 1}}}} + b{\psi _{{k}}}{\text{ = }}c{\delta _{{k}}} ,$ | (5) |
将上式写为更为一般的形式:
| $ {\psi _{{{k + 2}}}}{\text{ + }}a{\psi _{{{k + 1}}}} + b{\psi _{{k}}}{\text{ = }}c{\delta _{{{k + 1}}}}{\text{ + }}d{\delta _{\text{k}}} ,$ | (6) |
为便于使用向量表示,式(6)也可以写为:
| $ {\psi _{{{k + 2}}}}{\text{ + }}{a_1}{\psi _{{{k + 1}}}} + {a_2}{\psi _{{k}}}{\text{ = }}{b_1}{\delta _{{{k + 1}}}}{\text{ + }}{b_2}{\delta _{{k}}}。$ | (7) |
本文模型采用式(7)。从而,待辨识参数为
最小二乘(Least Square, LS)是指以最小化误差的平方和为原则来估计模型参数。在系统辨识领域,最小二乘算法能够简单有效的解决参数估计问题[13]。在船舶操纵运动模型参数估计方面,Yin等[14]、秦余刚等[15]均使用最小二乘算法或其改进的算法。其中,递推最小二乘(Recursive Least Square, RLS)算法具有无需存储全局数据、可递推计算、收敛速度较快、适用于在线计算等优点。本文使用RLS算法进行参数估计。
考虑如下系统:
| $ y(k) = {{\boldsymbol{\varphi }}^{\text{T}}}(k){\boldsymbol{\theta }}{\text{ + }}v(k)。$ | (8) |
其中:
则普通RLS算法[16]为:
| $ \left\{ {\begin{array}{*{20}{l}} {\hat \theta (k) = \hat \theta (k - 1) + {\boldsymbol{P}}(k){\boldsymbol{\varphi }}(k)e(k)},\\ {e(k) = y(k) - {{\boldsymbol{\varphi }}^{\text{T}}}(k)\hat \theta (k - 1)} ,\\ {{{\boldsymbol{P}}^{ - 1}}(k) = {{\boldsymbol{P}}^{ - 1}}(k - 1) + {\boldsymbol{\varphi }}(k){{\boldsymbol{\varphi }}^{\text{T}}}(k)} 。\end{array}} \right. $ | (9) |
其中,
从系统辨识原理来看,数据-模型类-误差准则是进行参数辨识的三要素。基于此,本文采用RLS算法进行实船操纵运动模型参数辨识的完整技术路线,如图4所示。主要环节包括:
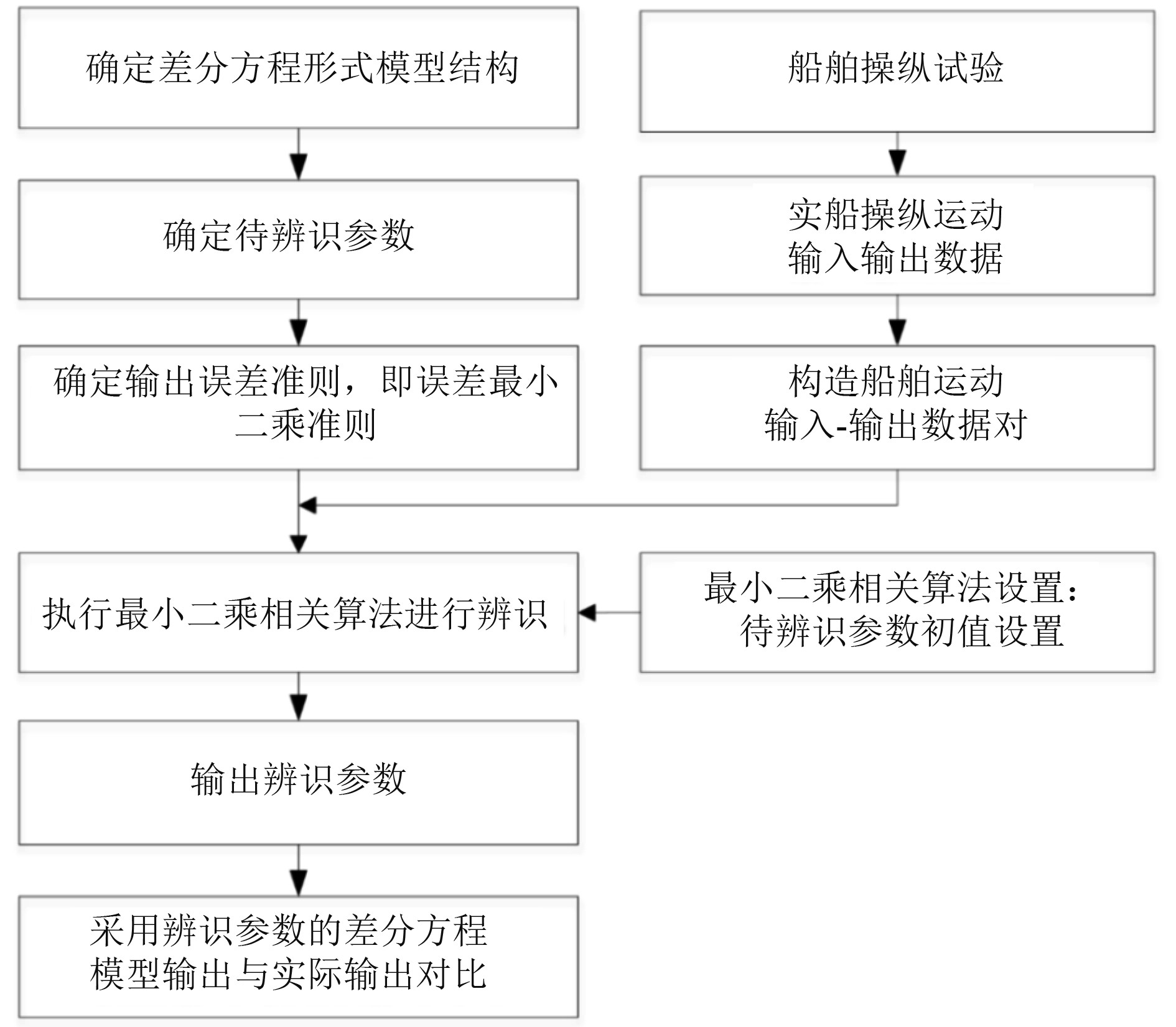
|
图 4 基于RLS进行船舶运动模型参数辨识的技术路线 Fig. 4 The technical route of parameter identification of ship motion based on RLS |
1)设计船舶操纵试验,获得进行系统辨识所需的船舶运动输入输出数据;
2)确定模型结构、待辨识的参数(见式(7));
3)选定误差准则,即误差最小二乘准则;
4)设置RLS算法初值、待辨识参数初值,执行RLS进行辨识,同步输出辨识结果;
5)将辨识参数应用于所选模型,施加同样操舵进行激励,得到模型输出;模型输出与实际输出进行比对,分析参数辨识结果及模型质量。
4 结果及分析考虑式(7)的模型,设待估参数初值为0,协方差
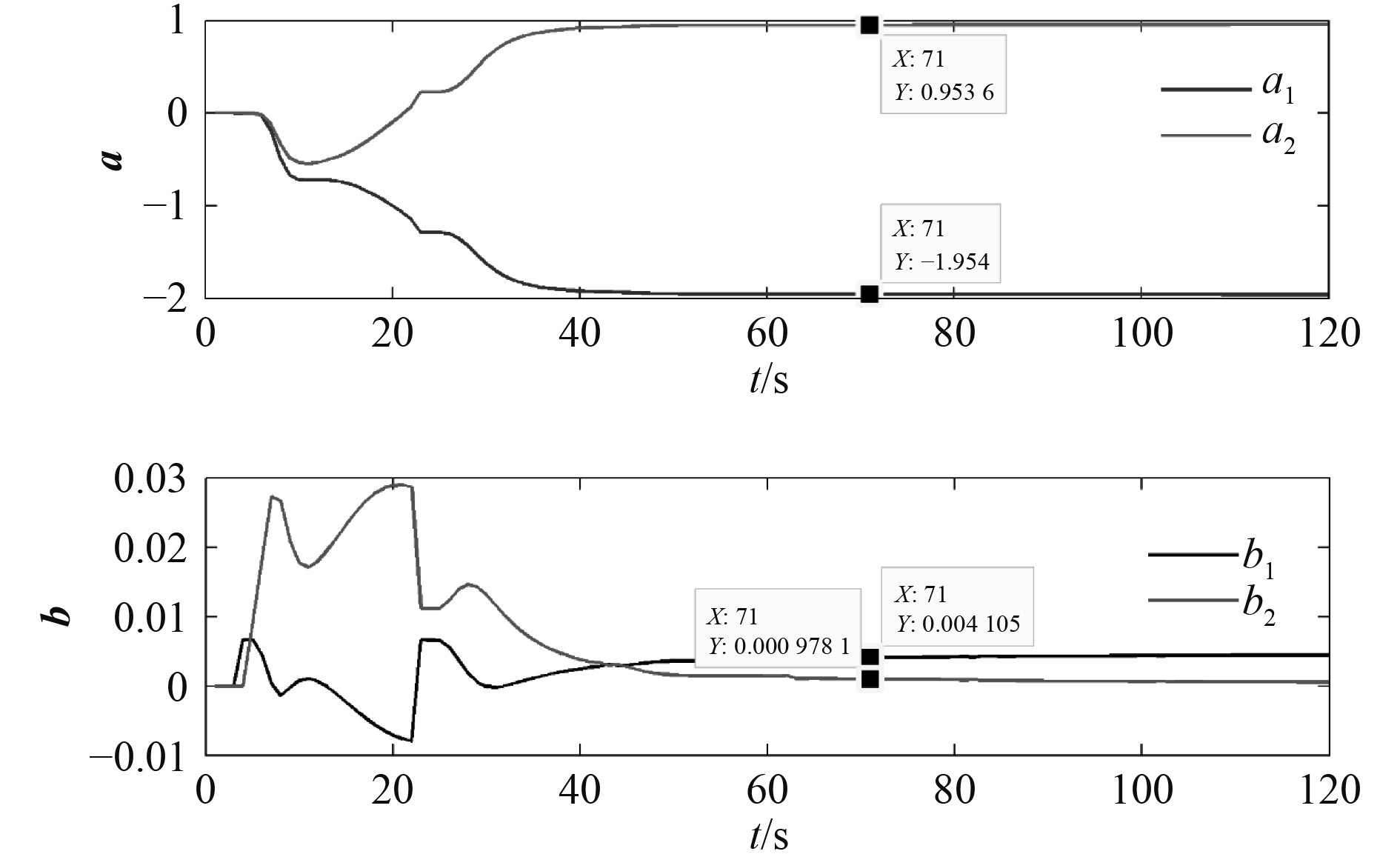
|
图 5 基于RLS的各参数辨识过程 Fig. 5 The process of parameter identification based on RLS |

|
图 6 使用辨识参数的模型输出与观测输出对比 Fig. 6 The comparison of system output and observation output |
图中,mst表示观测到的实船输出(运动状态,即航向),mdl表示相同的操舵时,使用辨识所得参数的数学模型输出。由图可见,使用辨识参数的差分方程模型能够较好拟合观测数据,表明辨识所得参数具有较高的精度,使得模型具有较高的质量,可以反映实船航向-舵角的响应特征。
综上所述,由参数辨识的过程和结果来看,本文采用的基于递推最小二乘算法进行差分方程型船舶运动模型参数辨识的方法具有较好的可行性,辨识所得参数具有较高精度,模型输出结果与实际观测结果能够很好拟合。
5 结 语模型参数辨识对完成船舶操纵运动建模具有重要意义。在系统辨识原理的框架下,设计一种基于RLS进行差分方程型模型参数辨识的技术路线。基于操纵试验数据,将技术路线应用于实船舵角-航向差分方程模型的参数辨识。应用结果表明,本文提出的技术路线具有较好的可行性,能够准确完成船舶舵角-航向运动模型的多参数辨识,使用辨识参数的模型输出值与实际观测输出值相近。本文基于操纵试验、使用RLS的实船运动模型参数辨识技术路线流程简单、适用性强,便于工程实现,具有一定的工程应用价值。RLS具有在线实时计算的特点,本文基于RLS的方法能够为船舶运动模型参数的自动辨识、在线辨识等提供方法支持,这对于提高船舶运动建模工作效率和建模精度、基于在线辨识进行操纵运动控制等具有支持作用。
| [1] |
张秀凤, 王晓雪, 孟耀等. 船舶运动建模与仿真研究进展及未来发展趋势[J]. 大连海事大学学报, 2021, 47: 1-8. ZAHNG Xiu-feng, WANG Xiao-xue, MENG Yao, et al. Research progress and future development trend of ship motion modeling and simulation[J]. Journal of Dalian Maritime University, 2021, 47: 1-8. DOI:10.16411/j.cnki.issn1006-7736.2021.01.001 |
| [2] |
赵大明, 施朝健, 彭静. 应用扩展卡尔曼滤波算法的船舶运动模型参数辨识[J]. 上海海事大学学报, 2008(3): 5-9. ZHAO Da-ming, SHI Zhao-jian, PENG Jing. Parameter identification to motion model of ship by extended Kalman filter[J]. Journal of Shanghai Maritime University, 2008(3): 5-9. |
| [3] |
王雪刚, 邹早建, 任如意, 等. 基于支持向量机的四自由度船舶操纵运动黑箱建模[J]. 中国造船, 2014, 55(3): 147-155. WANG Xue-gang, ZOU Zao-jian, REN Ru-yi, et al. Black-Box modeling of ship maneuvering motion in 4 degrees of freedom based on support vector machines[J]. Shipbuilding of China, 2014, 55(3): 147-155. |
| [4] |
王雪刚, 邹早建, 刘程. 基于支持向量机的四自由度船舶操纵运动盲预报[J]. 船舶力学, 2014: 1013-1023. WANG Xue-gang, ZOU Zao-jian, LIU Cheng. Blind prediction of ship manoeuvring motion in 4 degrees of freedom based on support vector machines[J]. Journal of Ship Mechanics, 2014: 1013-1023. |
| [5] |
孙健, 陈永冰, 周岗, 等. 高速舰船的运动模型适用性分析及海浪中的操纵仿真试验[J]. 舰船科学技术, 2018, 40(1): 41-45+51. SUN Jian, CHEN Yong-bing, ZHOU Gang, et al. The applicability analysis of the model of high-speed ship and the simulated maneuvering test in waves[J]. Ship Science and Technology, 2018, 40(1): 41-45+51. |
| [6] |
杨诚. 模型参数辨识在运动控制仿真系统的应用[J]. 舰船科学技术, 2020, 42(3A): 31-33. YANG Cheng. Application of model parameter identification in motion control simulation system[J]. Ship Science and Technology, 2020, 42(3A): 31-33. |
| [7] |
曹包华. 基于模型参数辨识的船舶运动控制仿真系统研究[D]. 吉林: 吉林大学, 2012. CAO Bao-hua. Research on the ship motion control simulation system base on parameter identification[D]. Jilin: Jilin University, 2012. |
| [8] |
毕革新. 递归神经网络的动态系统辨识及其在船舶运动控制中的应用研究[D]. 大连: 大连海事大学, 2009.
|
| [9] |
李光磊, 臧涛, 范邹, 等. 参数辨识在船舶运动控制中的研究与应用[J]. 船电技术, 2011, 31(4): 46-50,54. LI Guang-lei, ZANG Tao, FAN Zou, et al. Application of parameter identification to ship motion control[J]. Marine Electric & Electronic Engineering, 2011, 31(4): 46-50,54. |
| [10] |
丁彦侃, 俞孟蕻. 并行扩展卡尔曼滤波的船舶模型参数辨识研究[J]. 船舶工程, 2015, 37(1): 72-74. DING Yan-kan, YU Meng-hong. Parallel EKF identification methods for mathematics model of ship[J]. Ship Engineering, 2015, 37(1): 72-74. |
| [11] |
田延飞, 黄立文, 熊勇, 等. 利用新型蝙蝠算法辨识船舶运动模型参数[J]. 科学技术与工程, 2018, 18(8): 136-143. TIAN Yan-fei, HUANG Li-wen, XIONG Yong, et al. Parameter identification of ship motion model by using novel bat algorithm[J]. Science Technology and Engineering, 2018, 18(8): 136-143. |
| [12] |
TIAN Y. , HUANG L., XIONG Y., et al. Parameter identification of an ARX type ship motion model using system identification techniques[J]. International Journal of Smart Engineering, 2017, 1(4): 417-437. |
| [13] |
刘亢, 刘忠途, 李乐荣, 等. 永磁同步电机在线多参数辨识方法研究[J]. 微特电机, 2012: 4-7. LIU Kang, LIU Zhong-tu, LI Le-rong, ea al. Online multi-parameter identification method for permanent magnet synchronous motor[J]. Small & Special Electrical Machines, 2012: 4-7. |
| [14] |
YIN JC, ZOU Z J, XU F. Parametric identification of abkowitz model for ship manoeuvring motion by using partial least squares regression[J]. Journal of Offshore Mechanics and Arctic Engineering, 2015, 137: 1-8. |
| [15] |
秦余钢, 马勇, 张亮等. 基于改进最小二乘算法的船舶操纵性参数辨识[J]. 吉林大学学报(工学版), 2016, 46(3): 897-903. QIN Yu-gang, MA Yong, ZHANG Ling, et al. Parameter identification of ship’s maneuevering motion based on improved least square method[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(3): 897-903. |
| [16] |
张虎, 李正熙, 童朝南. 基于递推最小二乘算法的感应电动机参数离线辨识[J]. 中国电机工程学报, 2011, 31: 79-86. ZHANG Hu, LI Zheng-xi, TONG Zhao-nan. Off-line parameter identification of induction motor based on recursive least-squares algorithm[J]. Proceedings of the CSEE, 2011, 31: 79-86. |
 2023, Vol. 45
2023, Vol. 45

