船舶舷台作为船体结构的延伸,在结构形式上一般为变截面悬臂板架结构,具有承载雷达、天线、武器和其他设备的作用。相比船体其他结构,悬臂梁结构更易发生端部的挠度变形,因此其端部挠度是舷台结构设计过程中考虑的关键因素之一。
在变截面板架或变截面梁端部挠度的求解方法上,赵宽容[1]提出一种化变截面梁为等截面梁的积分计算方法,该方法将梁模型和所受载荷均进行等效处理,所得挠度计算结果误差较小,具有一定工程意义,但等效方法较为复杂。李银山等[2]基于独立一体化积分法,提出一种变截面梁的快速解析方法,可利用计算机语言实现对变截面梁挠度的快速求解。宋相道[3]针对矩形截面变截面悬臂梁,编制了3种荷载下的挠度公式计算表,但在适用范围上存在局限性。赵则昂等[4]归纳出一种对悬臂梁大挠度变形进行定量估计的方法,但局限于端部集中力的载荷形式。Zhou[5]提出一种新的分析弯曲理论,该理论考虑了薄壁箱梁腹板和翼缘的剪切变形,数值算例表明,该方法计算得到的弯曲应力和挠度与三维有限元模型分析结果吻合较好。周丹等[6]从6次拉格朗日插值函数出发,采用积分矩阵求解挠曲线近似微分方程,在下挠度变形下,计算了多种变截面梁模型的挠度,且与解析解比较吻合。
学者们在变截面梁结构的挠度变形计算方法上开展了大量的研究工作,但求解过程复杂。为此本文结合船级社规范,提出舷台结构的模型挠度计算的等效方法,将舷台结构等效为等截面的带板梁模型,可实现简单、快速的舷台端部挠度等效计算。同时,开展该方法挠度计算结果的安全性研究。基于典型舷台的初期设计方案,分别采用有限元法和等效方法,计算舷台结构的端部挠度,验证方法合理性,为舷台结构的轻量化设计提供参考。
1 舷台结构挠度计算的模型等效方法舷台结构一般是由舷台甲板、腹板、端部面板、面板、骨材等结构组成的悬臂板架结构,如图1所示。根据CCS规范,在开展板架结构挠度、强度计算时,可将其简化为带板-腹板-面板组成的带板梁模型,如图2所示。但简化后模型由于其截面模数变化,仍无法简单快速利用理论方法求解。

|
图 1 船舶舷台结构 Fig. 1 Ship gangway structure |

|
图 2 带板梁模型 Fig. 2 With Plate girder model |
针对图2所示的带板梁模型,在工程中可采用中点等效方法或端部等效方法对模型进行等效,即采用梁跨长中点对应的高度将变截面带板梁模型等效为等截面的带板梁模型,再开展后续的计算工作,端部等效方法同理,但上述2种方法存在挠度计算结果偏差大、过于保守的问题,不利于结构的轻量化设计。
为此提出一种重心位置的等效方法:首先根据带板梁模型中腹板的几何尺寸求得其型心位置,得到型心位置截面的腹板高度

|
图 3 等效方法示意图及等效后的等截面带板梁模型 Fig. 3 Schematic diagram of the equivalent method and the equivalent cross-section girder model with plate |
由于等效后模型为等截面的梁结构,文献[7-8]指出,在对“短粗”型梁的挠度变形时,应考虑剪切变形的影响。因此可根据理论力学,同时考虑弯曲变形和剪切变形,快速求得在设计载荷作用下端部的挠度,进而与设计要求或设计规范对比分析,对结构强度、设计方案进行初步判断。
2 等效模型挠度计算的安全性研究模型等效方法。其关键在于变截面带板梁模型中腹板的等效,带板及面板均保持原有尺寸。因此针对腹板等效前后,利用理论分析,开展等效模型挠度计算的安全性研究。
2.1 变截面悬臂梁模型针对图2所示的变截面带板梁模型,去除其带板和面板后,建立变截面悬臂梁模型,如图4所示。其中,模型长度为l,固定端高度为a,悬臂端高度为b,厚度为t,材料的弹性模量为E。左端边界条件为刚性固定,右端自由,施加竖直向下的均布线载荷q。

|
图 4 矩形截面变截面梁模型示意图 Fig. 4 Schematic diagram of the beam model with rectangular section and variable section |
王利平[9]提出一种变截面悬臂梁挠度计算方法,该方法挠度变形表达形式较为简单,且与积分法和数值仿真所得结果十分吻合,但仅局限于截面为矩形的简单变截面梁,无法利用该方法对图2所示的带板梁模型挠度进行求解。本文近似认为该方法所得结果为变截面悬臂梁端部挠度计算的精确解,根据参考文献,图4所示的矩形截面变截面悬臂末端挠度为:
| $ w_b = \frac{q}{{Et}}\left( {{\zeta _m}\frac{{1.5{l^4}}}{{{{\text{a}}^3}}} + {\zeta _v}\frac{{1.56{l^2}}}{a}} \right) 。$ | (1) |
其中:
| $ {\zeta _m} = 4{\left( {\frac{a}{{a - b}}} \right)^3}\left( {\frac{{2{a^2} + 5ab - {b^2}}}{{2{a^2}}} - \frac{{3b}}{{a - b}}\ln \frac{a}{b}} \right) ,$ | (2) |
| $ {\zeta _v} = 2\left( {\frac{a}{{a - b}}} \right)\left( {1 - \frac{a}{{a - b}}\ln \frac{a}{b}} \right) 。$ | (3) |
根据本文提出等效方法对图4所示的矩形截面变截面梁进行等效,等效后模型高度为
| $ {h_g} = \frac{2}{3}\frac{{{a^2} + ab + {b^2}}}{{a + b}} 。$ | (4) |
进而得出几何形心处的截面惯性矩
| $ I = \frac{{{{t}}{{{h}}_{{g}}}^3}}{{12}},$ | (5) |
| $ A = t{h_g}。$ | (6) |
考虑梁的弯曲变形和剪切变形,在均匀分布线载荷q作用下,其末端挠度为:
| $ {{{w}}_{{g}}} = \frac{{q{l^4}}}{{8EI}} + \frac{{1.2q{l^2}}}{{2GA}} = \frac{q}{{Et}}\left( {\frac{{1.5{l^4}}}{{{h_{\text{g}}}^3}} + \frac{{1.56{l^2}}}{{{h_g}}}} \right) 。$ | (7) |
首先定义无量纲参数m和n,其中m=l/a,即悬臂梁长度与固定端高度的比值,令m≥2;n=b/a,即悬臂端高度与固定端高度的比值。n大于0且小于1,则有:
| $ {w_{b}} = \frac{q}{{Et}}\left( {1.5{{{m}}^4}{\zeta _m} + 1.56{m^2}{\zeta _v}} \right)a ,$ | (8) |
| $\begin{split} {w_g} = & \frac{q}{{Et}}\left( {\frac{{1.5{l^4}}}{{{h_{\rm{g}}}^3}} + \frac{{1.56{l^2}}}{{{h_g}}}} \right){\rm{ = }}\\ & \frac{q}{{Et}}\left[ {\frac{{81{m^4}{{(n + 1)}^3}}}{{16{{({n^2} + n + 1)}^3}}} + \frac{{117{m^2}(n + 1)}}{{50({n^2} + n + 1)}}} \right]a。\end{split}$ | (9) |
式中:
| $ {\zeta _m} = \frac{4}{{{{\left( {1 - n} \right)}^3}}}\left( {\frac{{2 + 5n - {n^2}}}{2} + \frac{{3n}}{{1 - n}}\ln n} \right) ,$ | (10) |
| $ {\zeta _v} = \frac{2}{{1 - n}}\left( {1 + \frac{1}{{1 - n}}\ln n} \right)。$ | (11) |
定义函数
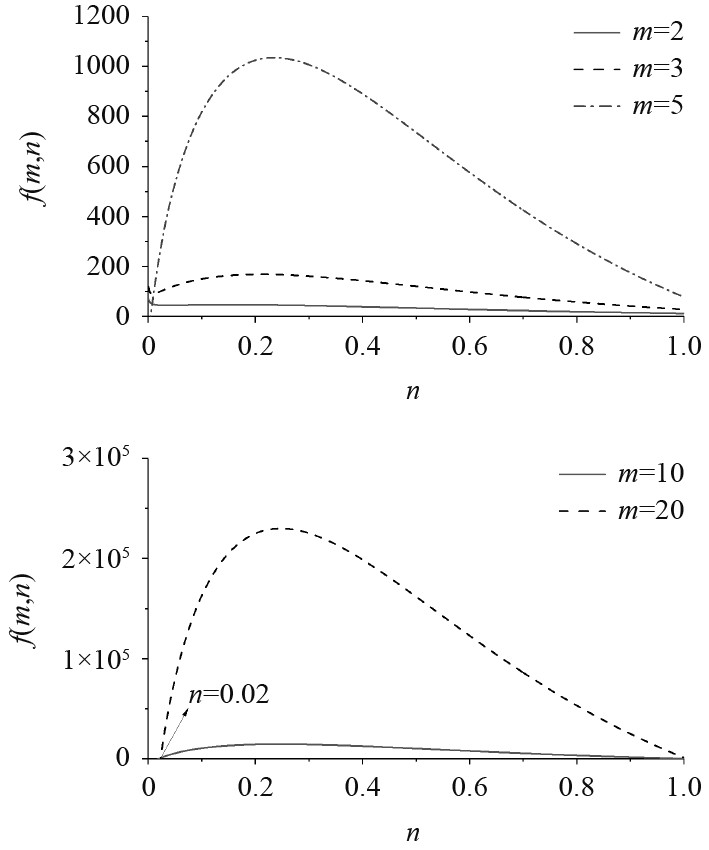
| $ \begin{split} f(m,n) = & \frac{{Et}}{{qa}}\left( {{w_g} - {w_b}} \right) = \left[ {\frac{{81{m^4}{{(n + 1)}^3}}}{{16{{({n^2} + n + 1)}^3}}} + \frac{{117{m^2}(n + 1)}}{{50({n^2} + n + 1)}}} \right] - \\ & \left( {1.5{{\rm{m}}^4}{\zeta _m} + 1.56{m^2}{\zeta _v}} \right)。\end{split} $ | (12) |
其中:m≥2,0<n<1。
可以看出函数
|
图 5
m取不同值时f(m,n)曲线
Fig. 5
|
可以看出,在m=2,3时,f(m,n)恒大于0;在m=5,10,20时,存在部分区间内的n值使得f(m,n)<0,但区间内n的值较小,最大为0.02,在悬臂梁设计时不会采用该形式。
综上可以看出,等效后的腹板柔度增大,因此整体的柔度也将增大。在采用本文提出的模型等效方法开展舷台结构的端部挠度计算时,可在不进行仿真计算的条件下,对挠度进行简单、快速的等效计算,其挠度计算结果是偏于安全的;同时相比于中点等效法和端部等效法,本文提出的等效方法中腹板高度取值更大,所以更加接近真实解。
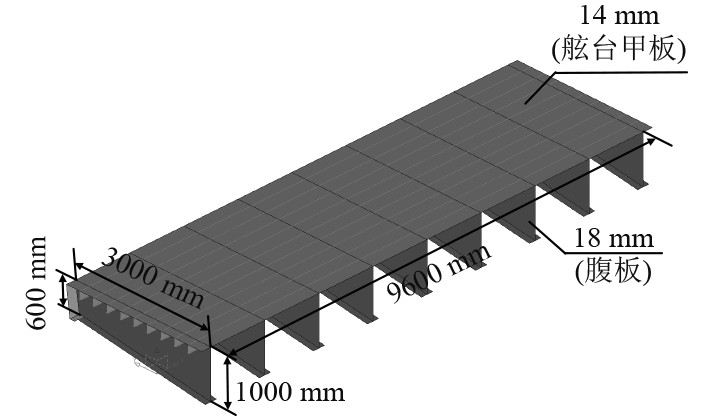
3 舷台结构端部挠度计算分析根据某船设计需求,设计宽度为3 m,长度为9.6 m的舷台结构,且端部挠度小于7.5 m(CCS规范要求,挠度小于l/400倍的悬臂长)。参考以往设计经验,设计如图6所示的舷台结构,其中舷台甲板厚度为14 mm,腹板厚度为18 mm,面板尺寸为20×250 mm,舷台甲板下方均匀布置9根T16球扁钢骨材,使用材料为钢材。采用有限元法和等效计算方法分别对该舷台端部挠度进行求解。
|
图 6 舷台结构模型 Fig. 6 Structural model of the gangway |
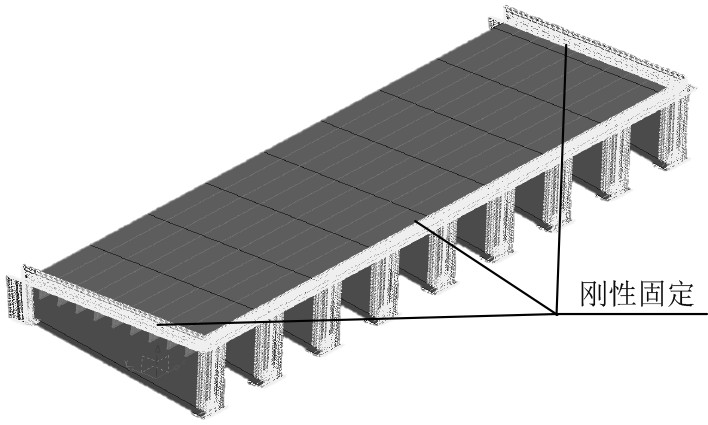
根据初步设计方案,建立如图7所示的有限元模型,模型边界条件为悬臂端自由。其余三边刚性固定,且为进一步提高计算精度,采用较小的尺寸进行网格划分,网格尺寸为20 mm。
|
图 7 舷台结构有限元模型及边界条件 Fig. 7 Finite element model and boundary conditions of the gangway structure. |
考虑到船舶舷台结构与简单的工字型变截面梁存在一定差异,具体差异包括骨材的有无、悬臂端面板、舷台长度等。为此,建立多个舷台结构模型,初步探究上述差异对端部挠度的影响。此外,根据CCS规范,将舷台简化为带板-腹板-面板的工字型截面变截面带板梁模型,其中带板宽度为663 mm,所建立的模型如表1和图8所示。
|
|
表 1 模型参数 Tab.1 Model parameters |

|
图 8 模型5有限元模型 Fig. 8 Finite element model of model 5 |
在设计载荷上,由于该舷台位于首部区域,经常受到波浪的抨击载荷,经综合考虑取均布载荷大小为250 kPa。由于腹板间距为1.2 m,模型5的计算载荷为250 kPa×1.2 m=300 kN/m。
3.1.2 模型端部挠度计算结果在进行挠度计算时,为便于分析,模型1~模型5的挠度计算结果均为腹板上的最大挠度,模型计算结果和模型1的位移云图如表2和图9所示。
|
|
表 2 挠度计算结果 Tab.2 Deflection calculation results |

|
图 9 舷台位移云图 Fig. 9 The gangway displacement cloud map |
从模型1~模型4的挠度结果可以看出,悬臂端面板有无、骨材有无和舷台长度对挠度计算结果影响较小,最大误差为1.6%。而模型5的计算结果与模型1差异较大,其原因是CCS规范中带板宽度的计算方法是偏于安全的。
3.2 等效计算方法求解舷台挠度根据提出的等效计算方法对模型5进行等效。首先确定腹板结构的几何型心位置,进一步求得型心位置对应的腹板高度为

|
图 10 等效后带板梁模型 Fig. 10 Equivalent rear belt girder model with plate |
等效后模型为等截面梁,根据弹性力学理论,考虑梁的弯曲变形和剪切变形。在均布线载荷q=300 kN/m的作用下,其末端挠度wg=ql4/8 EI+1.2 ql2/2 GA=6.81 mm。
从上述计算结果可以看出:1)等效后的模型较等效前(模型5)的挠度计算结果更大,误差约为44%,但等效计算方法无需有限元仿真计算,计算效率高,且可保障结果的安全性,对舷台结构的轻量化设计具有一定参考价值。2)采用等效计算方法,端部挠度计算结果为6.85 mm,与设计要求的7.5 mm相比,还有一定裕度,在结构设计上可综合考虑其他因素,进一步开展舷台结构进行轻量化设计工作。
4 结 语参考工程中在变截面梁挠度求解时常用的中点等效法和端部等效法,提出一种将船舶舷台等效为等截面带板梁模型的等效方法,开展该等效方法的安全性研究。在此基础上,结合某船舷台结构的初步设计方案和设计要求,采用有限元法和本文提出的等效计算方法,对舷台结构端部挠度进行计算,主要结论如下:
1)提出将船舶舷台等效为等截面带板梁模型的等效方法,其中等截面带板梁的带板宽度依照CCS规范选取,腹板高度为舷台腹板重心位置对应的高度。
2)舷台结构中骨材的有无、悬臂端面板、舷台长度等因素对端部挠度变形影响较小。
3)基于舷台结构等效后的等截面带板梁模型,考虑带板梁的弯曲变形和剪切变形,可简单快速地对舷台端部挠度求解,所得到的端部挠度计算结果是安全的,且相比工程中常用的中点等效法、端部等效法更接近真实解。
| [1] |
赵宽荣. 化变截面为等截面求梁的变形[J]. 陕西工学院学报(自然科学版), 1996, 12(1): 74-77. |
| [2] |
李银山, 官云龙, 李彤, 等. 求解变截面梁变形的快速解析法[J]. 工程力学, 2015, 32(S1): 116-121+141. LI Yin-shan, GUAN Yun-long, LI Tong, et al. A fast analytical method for solving the deformation of beams with variable cross-sections[J]. Engineering Mechanics, 2015, 32(S1): 116-121+141. |
| [3] |
宋相道. 矩形变截面悬臂梁的挠度计算公式[J]. 建筑结构, 1998(7): 58. DOI:10.19701/j.jzjg.1998.07.018 |
| [4] |
赵则昂, 邓宗白, 宋安平. 悬臂梁大挠度变形的近似估计法[J]. 力学与实践, 2014, 36(3): 341-344+366. ZHAO Ze-ang, DENG Zong-bai, SONG An-ping. Approximate estimation method for large deflection deformation of cantilever beams[J]. Mechanics and Practice, 2014, 36(3): 341-344+366. DOI:10.6052/1000-0879-13-124 |
| [5] |
周丹, 王应军, 孙明清, 等. 小挠度变截面梁的积分矩阵法求解[J]. 江苏师范大学学报(自然科学版), 2016, 34(2): 68-71. |
| [6] |
ZHOU Maoding, ZHANG Yuanhai, LIN Pengzhen, et al. A new practical method for the flexural analysis of thin-walled symmetric cross-section box girders considering shear effect[J]. Thin-Walled Structures, 2022, 171.
|
| [7] |
周期源, 高轩能. 剪切变形对变截面梁挠度的影响分析[J]. 工业建筑, 2006(S1): 277-279+276. ZHOU Yuan, GAO Xuan-neng. Analysis of Influence of Shear Deformation on Deflection of Variable Section Beams[J]. Industrial Architecture, 2006(S1): 277-279+276. DOI:10.3321/j.issn:1000-8993.2006.z1.081 |
| [8] |
周期源, 高轩能. 考虑剪切变形影响时变截面梁的挠度计算[J]. 南昌大学学报(工科版), 2006(3): 295-298. ZHOU Yuan, GAO Xuan-neng. Deflection calculation of time-varying section beams considering the influence of shear deformation[J]. Journal of Nanchang University (Engineering Science Edition), 2006(3): 295-298. |
| [9] |
王利平. 一种变截面悬臂梁挠度计算方法研究[J]. 河南科技, 2018(22): 122-124. DOI:10.3969/j.issn.1003-5168.2018.22.046 |
 2023, Vol. 45
2023, Vol. 45
