潜射弹道导弹通常采用平台式惯性导航系统,其初始对准的方式与捷联式惯性导航系统不同,通常采用先平台调平再方位对准的方式进行。当前,传递对准技术研究主要针对捷联式惯性导航系统,对于平台式惯性导航系统的传递对准算法研究较少。
与航空运载平台相比,潜艇机动能力有限,速度、位置和姿态等运动参数的变化率较小。受海流和风浪等因素的影响,艇体可能存在较大变形角[1,2],从而影响传递对准精度。针对潜艇航行时运动参数变化速率慢、变化范围小的特点[3],分析传递对准模型,研究适用于潜射弹道导弹传递对准匹配算法,并结合潜艇航行试验数据,分析有利于进行传递对准的运动方式,为潜射弹道导弹传递对准技术的发展提供参考。
1 传递对准模型在潜射弹道导弹中,初始对准通过水平调整(简称调平)和方位对准来实现。惯性平台的方位对准是指在惯性平台调平后,将惯性测量坐标系OnXn轴向发射坐标系的OgXg轴的对准过程。在进行瞄准时主、子惯导之间存在失准角。主、子惯导对载体运动参数测量的输出值就会存在差值,这些差值能不同程度地反映出失准角的大小,从而可利用这些差值估计主、子惯导之间的失准角。
在进行平台方位对准时,需先确定射击方位OXg和平台坐标系OXps方位之间的夹角

|
图 1 方位传递对准示意图 Fig. 1 Azimuth alignmen diagram |
可得关系式
| $ \delta = {A_g} - \gamma。$ | (1) |
从而只要求得子惯导与主惯导之间的失准角
由于平台式惯性导航系统采用实际物理平台,加速度计输入轴与平台坐标系轴线平行,速度误差信息反映了两平台失准角,因此可采用速度匹配折方式;载体的姿态角由框架轴上的姿态角传感器输出,无法直接提供载体角速度,因而在传递对准过程中可采用姿态角匹配的方式。
1)速度误差
主惯性与子惯导的速度误差模型可表示为:
| $ \delta \dot v = {{\boldsymbol{\phi}} _ {\boldsymbol{\times}} }\dot W_s^s + (2\omega _{ie}^n + \omega _{en}^n) \times \delta v 。$ | (2) |
式中:
2)框架角误差
设主惯导框架坐标系与子惯导框架坐标系间的转换矩阵为
| $ \delta u = {{\boldsymbol{\phi}} _ {\boldsymbol{\times}} }{\omega _z} + \left( {I - {\boldsymbol{C}}_{\boldsymbol{m}}^{\boldsymbol{s}}} \right){\omega _z} 。$ | (3) |
1)速度匹配方程
主惯性输出的速度信息为
| $ \delta v = {v_s} - {v_m} + {\varepsilon _v}。$ | (4) |
式中,
2)框架角匹配方程
主惯导测得的框架角为
| $ \delta u = {u_s} - C_m^s{v_m} + {\varepsilon _u} 。$ | (5) |
式中,
由于潜艇在水下机动能力有限,结合速度匹配、姿态匹配的方法,采用速度+框架角的匹配方式,传递对准算法的状态量为:
| $ X = [\delta v,\delta u,\phi ,{\varepsilon _v},{\varepsilon _u}]。$ | (6) |
在传递对准过程中采用速度+框架角匹配模型[4-6]。系统状态方程为:
| $ \dot X = FX + w 。$ | (7) |
采用“速度+框架角匹配”的传递对准方案,是用主惯导和子惯导的输出速度和框架角之差作为观测量。
| $ \delta z = {[\delta {v_x},\delta {v_y},\delta {v_z},\delta {u_x},\delta {u_y},\delta {u_z}]^{\rm{T}}},$ | (8) |
由此得到的量测方程为:
| $ z = HX + \delta z。$ | (9) |
平方根滤波一方面可减小对计算机字长的要求,从而提高滤波的精度;另一方面可时刻保证
为了适应潜艇航行过程中运动参数变化率小的情形,在设计传递对准滤波器的设计时,希望滤波器同时具有平方根滤波和H∞滤波的优点,即:滤波算法具有较好的鲁棒性;滤波算法能够尽快收敛,减少滤波时间;能够给出最优的状态估计,提高状态估计的精度。为此本文提出一种平方根/H∞混合滤波方法。
| $ \hat X_{k + 1\_2}^{} = {F_k}{\hat X_{k\_2}} + {F_k}{K_{k\_2}}({Z_k} - {H_k}\hat X_{k\_2}^{})。$ | (10) |
在H∞滤波中,状态更新方程为[10]:
| $ \hat X_{k + 1\_\infty }^{} = {F_k}{\hat X_{k\_\infty }} + {F_k}{K_{k\_\infty }}({Z_k} - {H_k}\hat X_{k\_\infty }^{})。$ | (11) |
2种滤波算法的状态更新方程在此形式上相同,本质区别在于增益矩阵的计算方式及每次测量更新得到的值不同。
在平方根滤波的增益矩阵为:
| $ K_{k\_2}^{} = a{S_k}\phi 。$ | (12) |
在H∞滤波的增益矩阵为:
| $ {K_{k\_\infty }} = {P_k}{\left[ {I - \theta {{\bar S}_k}{P_k} + H_k^{\text{T}}R_k^{ - 1}{H_k}{P_k}} \right]^{ - 1}}H_k^{\text{T}}R_k^{ - 1}。$ | (13) |
同时,与增益矩阵相对应的估计均方误差也不相同。在平方根滤波中估计均方误差为
设平方根滤波器估计均方误差的迹为
| $\begin{aligned} & {K_{k\_2/\infty }} = \\ & \left\{ {\begin{array}{*{20}{l}} {\dfrac{{tr{p_2}}}{{tr{p_\infty } + tr{p_2}}}{K_{k\_2}} + \dfrac{{tr{p_\infty }}}{{tr{p_\infty } + tr{p_2}}}{K_{k\_\infty }}},\\{tr{p_\infty } \leqslant tr{p_2}} ,\\ {\dfrac{1}{{1 + tr{p_2} - tr{{p'}_2}}}{K_{k\_2}} + \dfrac{{tr{p_2} - tr{{p'}_2}}}{{1 + tr{p_2} - tr{{p'}_2}}}{K_{k\_\infty }}},\\{tr{p_\infty } > tr{p_2}}。\end{array}} \right. \end{aligned}$ | (14) |
式中:
将得到的增益矩阵分别代入平方根滤波器和H∞滤波中,并将其作为该滤波器的增益矩阵。从而可以得到一个修正后的平方根滤波器和一个修正后的H∞滤波器,状态更新方程分别为:
| $ \hat X_{k + 1\_2}^{} = {F_k}{\hat X_{k\_2}} + {F_k}{K_{k\_2/\infty }}({Z_k} - {H_k}\hat X_{k\_2}^{}),$ | (15) |
| $ \hat X_{k + 1\_\infty }^{} = {F_k}{\hat X_{k\_\infty }} + {F_k}{K_{k\_2/\infty }}({Z_k} - {H_k}\hat X_{k\_\infty }^{})。$ | (16) |
在平方根/H∞混合滤波器中,分别修正了平方根滤波器和H∞滤波器中的状态估计值,但没有改变各自的估计均方误差等其他参数的值。因而平方根滤波器和H∞滤波器中仍保留了各自信息,这保证了平方根滤波器和H∞滤波器各自的性能。
3 潜艇机动方式 3.1 变速直航运动变速直航运动可分为加速运动和减速运动,主要限制因素包括潜艇动力性能、海水阻力以及潜艇惯性等。为传递对准滤波算法提供的数据类型主要是速度。潜艇水下航行,考虑到隐蔽性因素和舵效和操艇安全问题,潜艇航速通常控制在某一区间内。在传递对准过程中,速度变化率的大小对于滤波估计的效果有明显影响。
在该变速直航运动中,经过500 s的加速,航行速度由2.65 m/s提高到3.03 m/s;航向角179.72°~180.43°变化区间为;横摇角变化区间为−0.34°~0.22°;纵摇角变化区间为−0.09°~0.57°。如图2和图3所示。
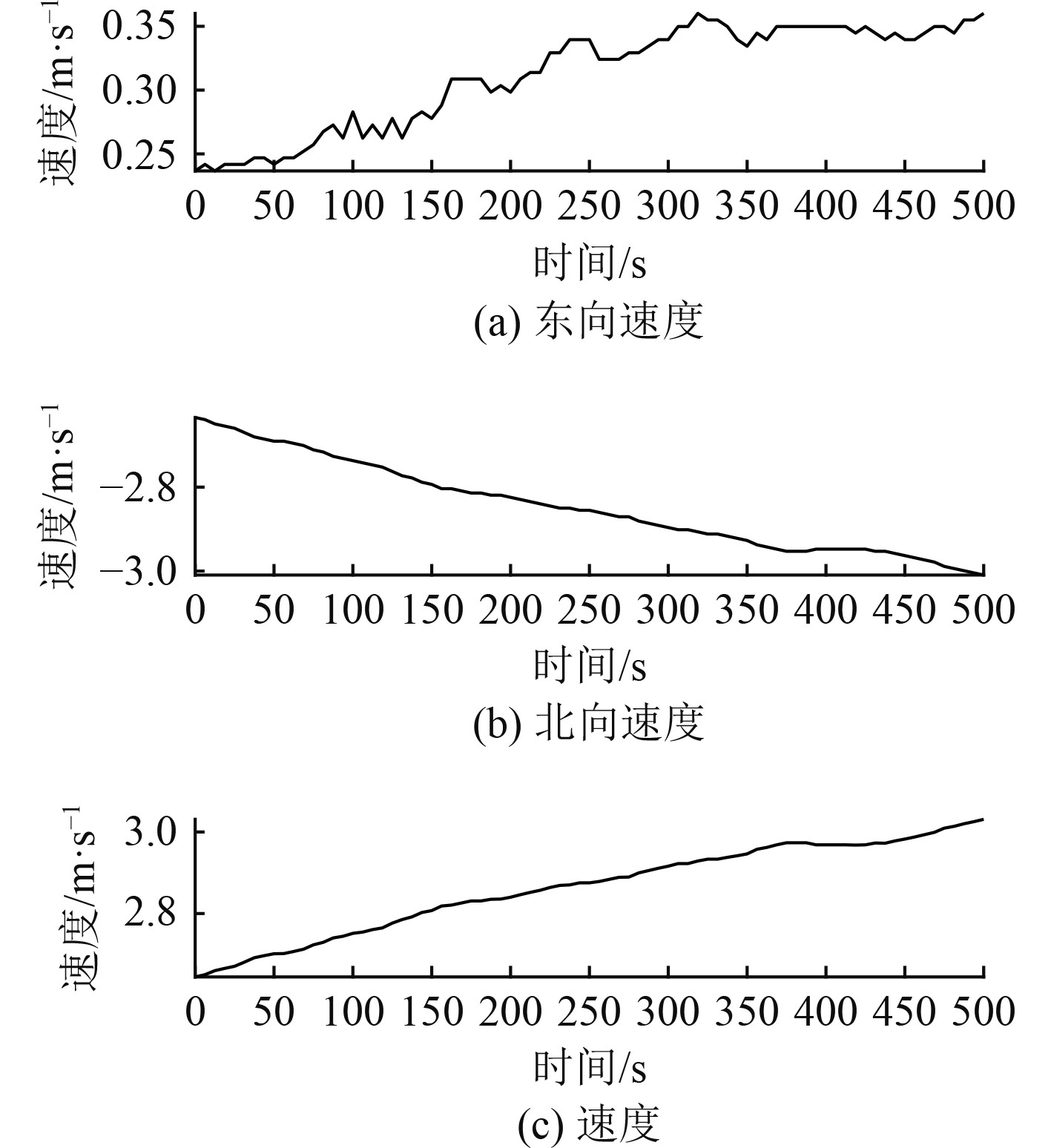
|
图 2 变速直航时的速度 Fig. 2 The speed of straight forward |

|
图 3 变速直航时惯导的框架角 Fig. 3 The attitude angle of straight forward |
转舵旋回时,艇体和舵力矩、流向螺旋桨的水流等条件发生改变,致使螺旋桨的推力发生变化,从而引起艇的航速变化。另一方面,艇在C形机动时,航向的变化会直接引起东向速度和北向速度的大范围变化。
在该C形机动中,航行速度变化区间为1.98~3.47 m/s;航向角由79.35°转至259.10°;横摇角变化区间为−0.04°~1.81°;纵摇角变化区间为−0.20°~0.69°。如图4和图5所示。
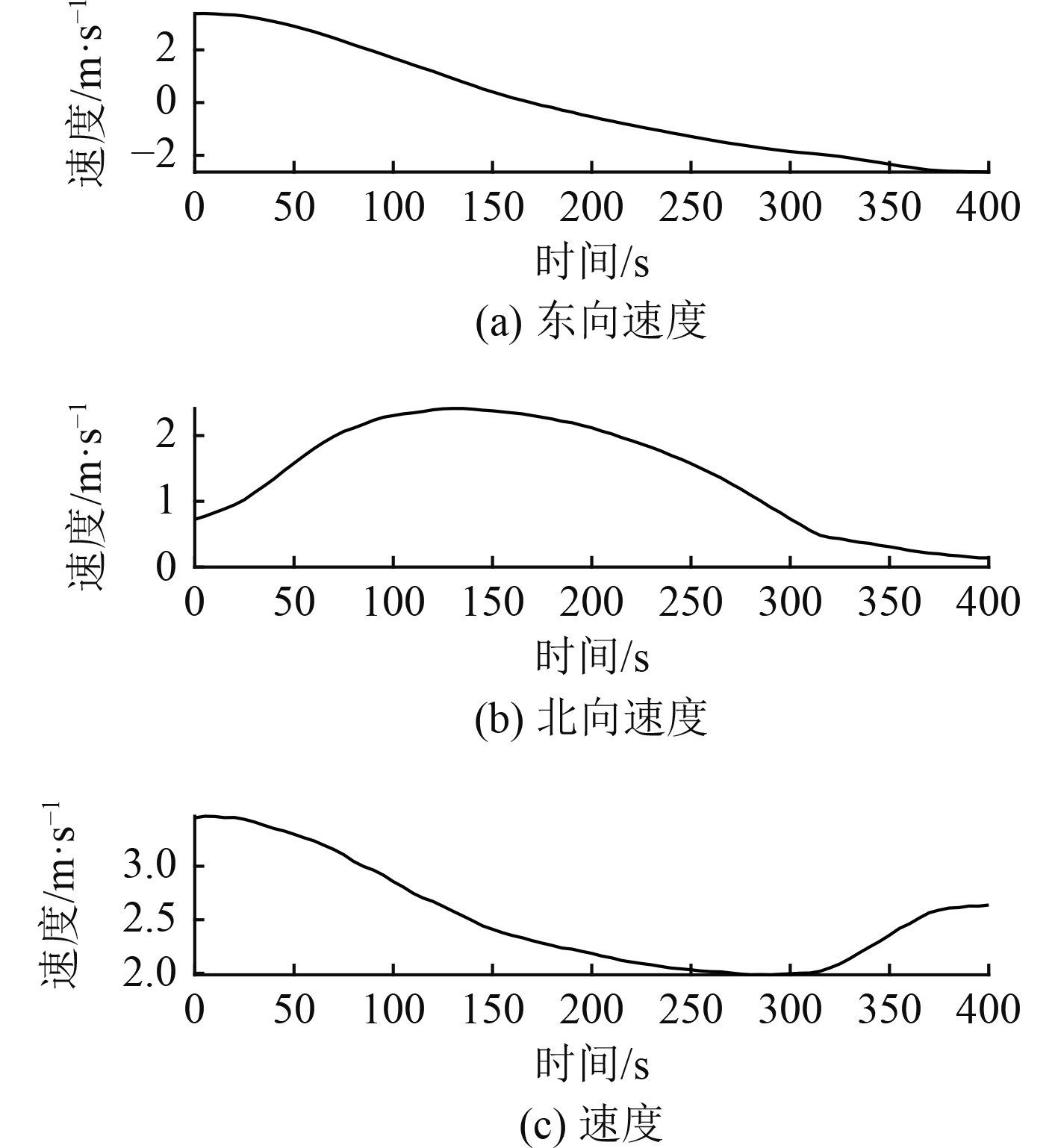
|
图 4 C形机动时的速度 Fig. 4 The speed of C-type maneuvering |
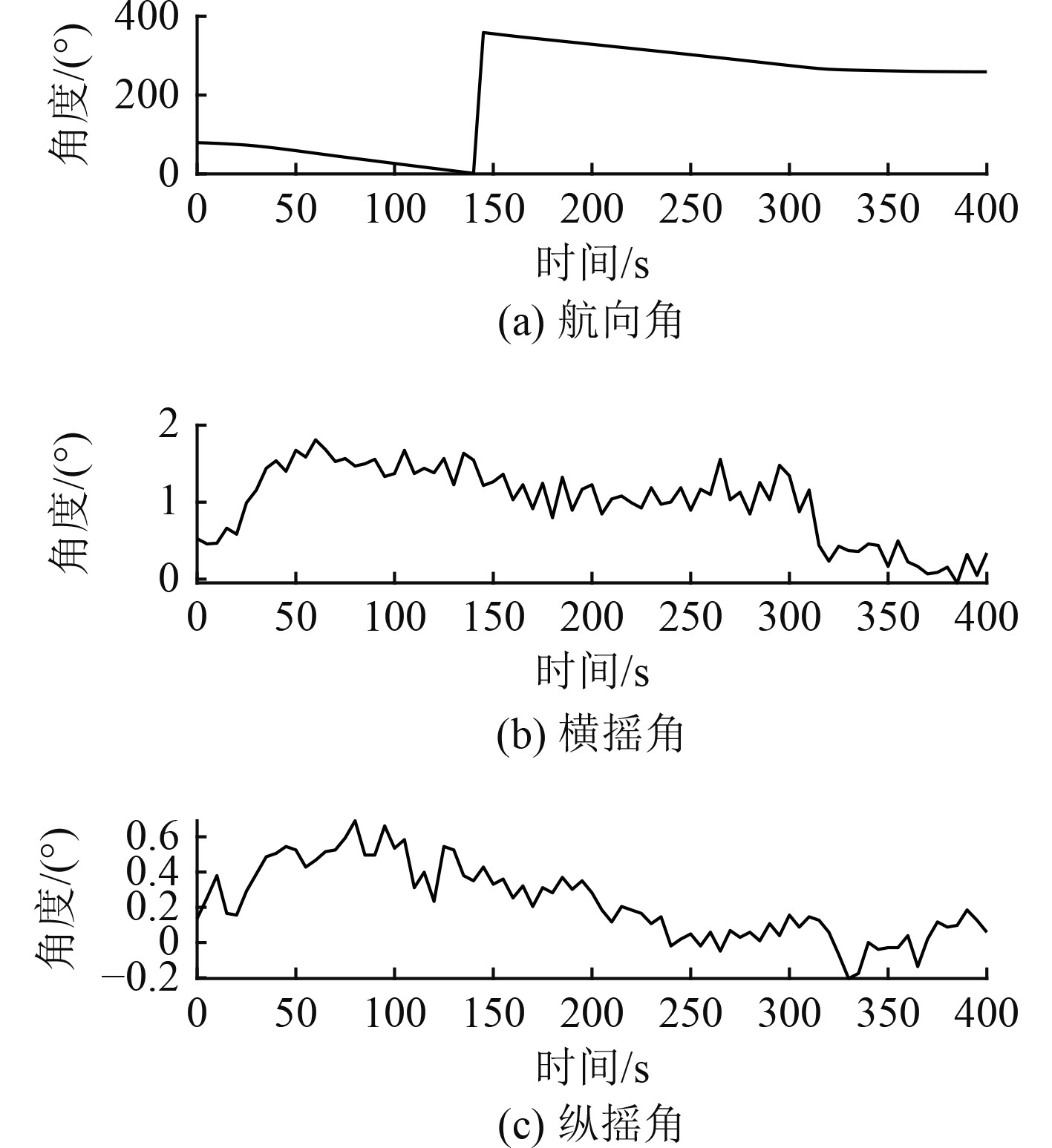
|
图 5 C形机动时惯导的框架角 Fig. 5 The attitude angle of C-type maneuvering |
S形机动可看成是由2个旋回方向相反的C形机动构成的。S形机动与C形机动的区别在于,潜艇在改变舵角的过程中侧向速度和横倾角会改变符号,对于提高系统的可观测性具有重要意义。
在该S形机动中,航行速度变化区间为2.10~5.16 m/s;航向角由328.40°转至143.18°再转至308.71°;横摇角变化区间为−9.22°~14.46°;纵摇角变化区间为−2.10°~2.27°。如图6和图7所示。
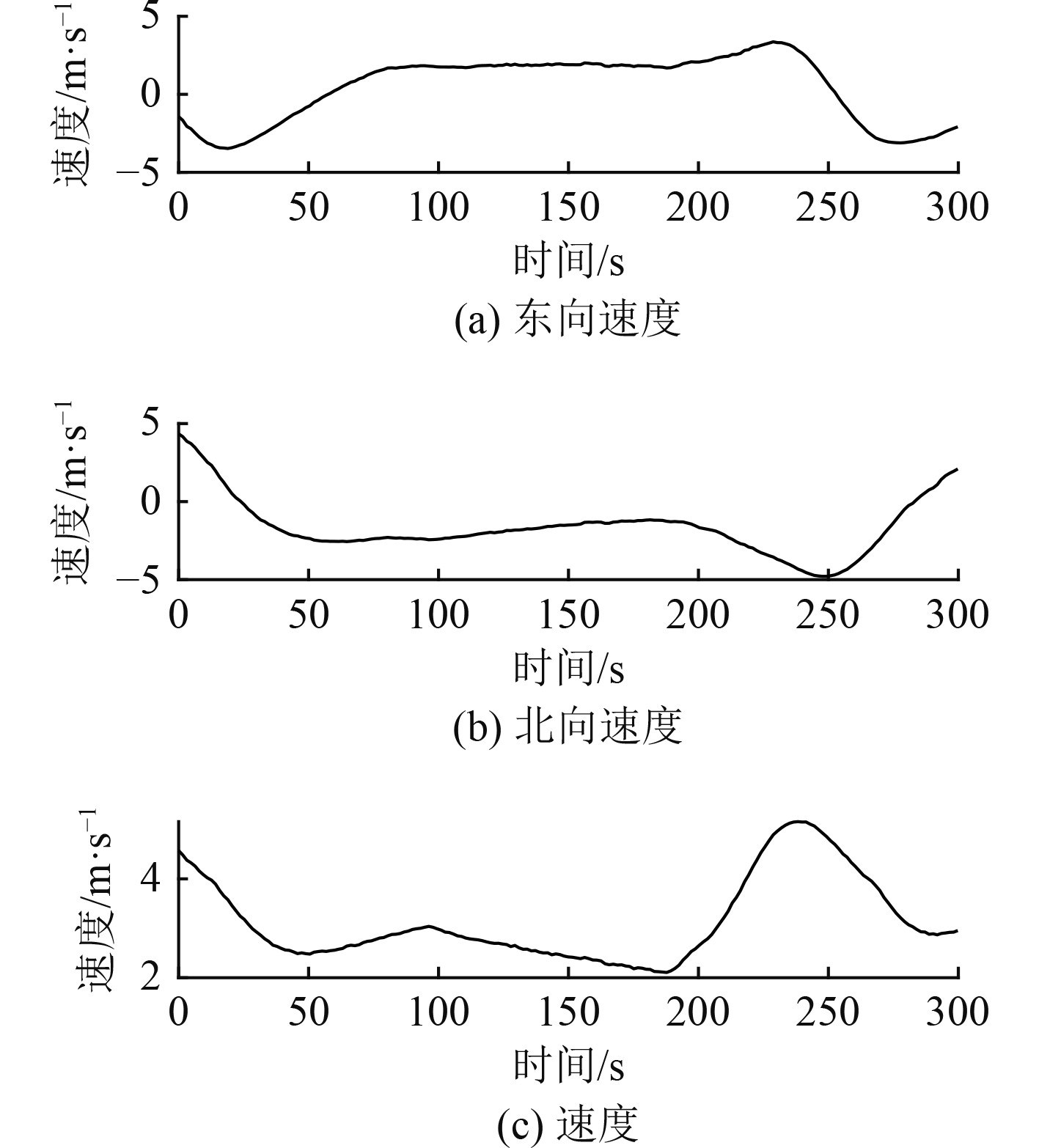
|
图 6 S形机动时的速度 Fig. 6 The speed of S-type maneuvering |

|
图 7 S形机动时惯导的框架角 Fig. 7 The attitude angle of S-type maneuvering |
潜艇进行变速直航运动时,在500 s的时间内,航速由6 kn变化到11.6 kn。速度变化为传递对准提供了观测量。
通过仿真计算发现,采用变速直航运动时,采用平方根滤波算法、H∞滤波算法和平方根/H∞混合滤波算法进行传递对准,均未得到完全收敛的方位失准角估计结果,如图8所示。
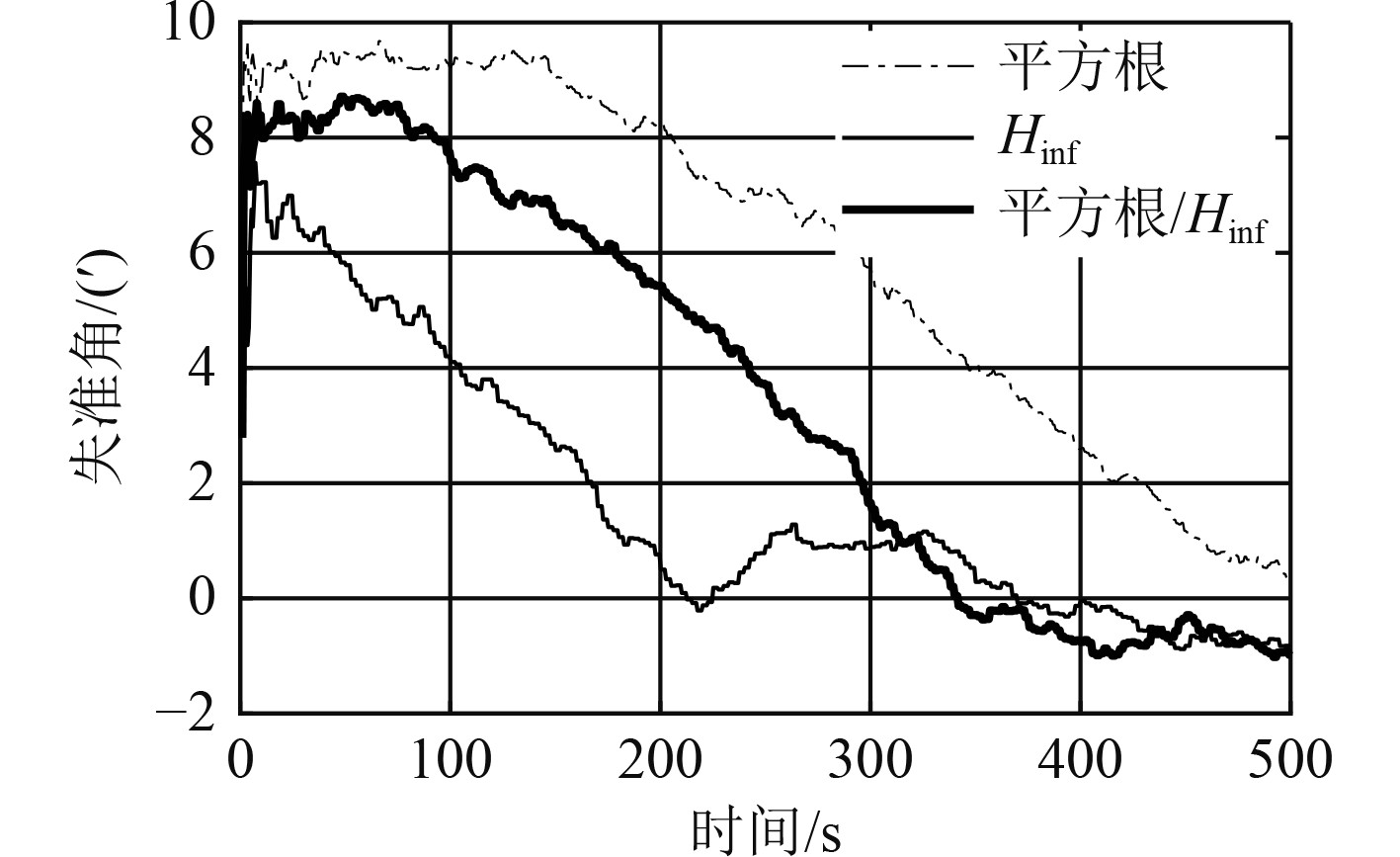
|
图 8 变速直航运动时方位失准角估计 Fig. 8 The azimuth misalignment angles in straight forward maneuvering |
潜艇进行C形运动时,在400 s的时间内,航速变化范围为8.3~9.7 kn;航向变化量为278.4°。在机动过程中速度和航向的变化为传递对准提供了观测量。
通过仿真计算发现,采用C形机动时,采用平方根滤波算法时,在332 s方位失准角估计值收敛,方位失准角估计误差平均为−0.3′;采用H∞滤波算法时,在214 s方位失准角估计值收敛,方位失准角估计误差平均为−0.8′;采用平方根/H∞混合滤波算法时,在183 s方位失准角估计值收敛,方位失准角估计误差平均为−0.3′,如图9所示。
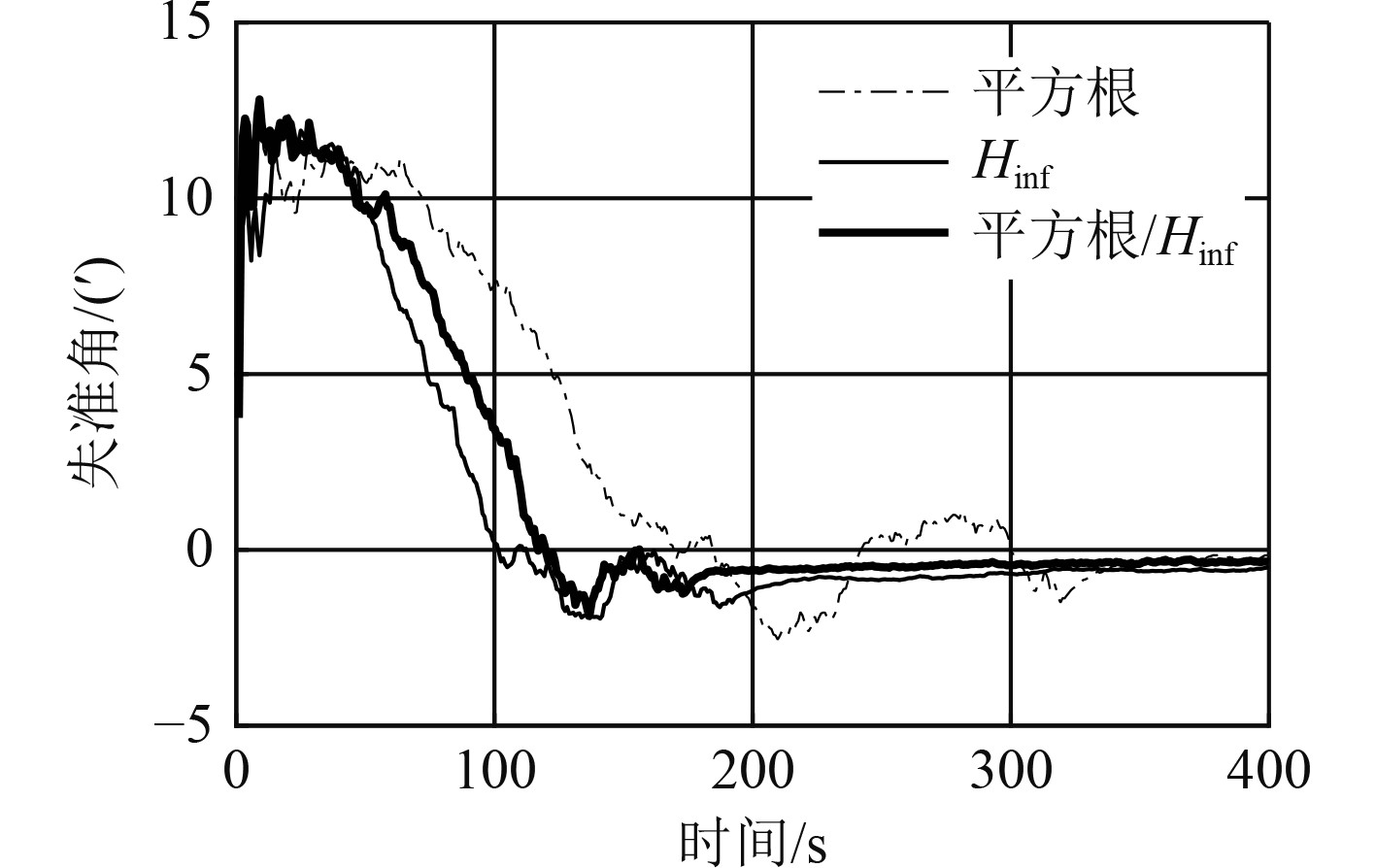
|
图 9 C形机动时方位失准角估计 Fig. 9 The azimuth misalignment angles in C-type maneuvering |
潜艇进行S形运动时,在300 s的时间内,航速变化范围为8.2~9.3 kn;航向变化量为134.7°。在机动过程中速度和航向的变化为传递对准提供了观测量。
通过仿真计算发现,采用S形机动时,采用平方根滤波算法时,在165 s方位失准角估计值收敛,方位失准角估计误差平均为−0.4′,在237 s后,方位失准角估计值进一步稳定,误差平均−0.3′;采用H∞滤波算法时,在145 s方位失准角估计值收敛,方位失准角估计误差平均为−0.6′,在250 s后,方位失准角估计误差平均值进一步减少为0.4′。采用平方根/H∞混合滤波算法时,在159 s方位失准角估计值收敛,方位失准角估计误差平均为−0.3′,在255 s后,角估计误差平均值进一步减少为0.2′。

|
图 10 S形机动时方位失准角估计 Fig. 10 The azimuth misalignment angles in S-type maneuvering |
通过仿真分析,基于平方根/H∞混合滤波的传递对准算法,其收敛速度优于平方根滤波算法,传递对准数度优于H∞滤波算法,算法的鲁棒性和估计精度均优于平方根滤波算法和H∞滤波算法。
采用变速直航机动方式进行对准时,算法收敛速度较慢,方位失准角较大;采用C形机动方式进行对准时,算法收敛速度中等,方位失准角估计比较准确;采用S形机动方式进行对准时,算法收敛速度较快,方位失准角估计比较准确。因此,为了提高传递对准的速度和精度应尽可能采用S形机动方式进行传递对准。
| [1] |
程建华, 王通达, 宋春雨, 等. 舰船捷联惯导传递对准的改进自适应滤波算法[J]. 系统工程与电子技术, 2016, 38(3): 638-643.
|
| [2] |
张力宁, 徐旭, 何昆鹏. 一种应变片估计挠曲变形的快速传递对准方法[J]. 哈尔滨工程大学学报, 2019, 40(6): 1142-1148.
|
| [3] |
陈建华, 王瑞臣, 徐利明. 传递对准技术在潜射导弹瞄准中的应用可行性分析[J]. 导弹与航天运载技术, 2012, 4: 42-44.
|
| [4] |
贺江涛, 刘宝宁, 蔺睿. 车载远程制导导弹传递对准方法研究[J]. 计算机测量与控制, 2020, 28(12): 130-134.
|
| [5] |
韩雪峰. 舰船惯导系统运动中传递对准方法研究[J]. 舰船科学技术, 2020, 42(11): 134-137. DOI:10.3404/j.issn.1672-7649.2020.11.027 |
| [6] |
史荣宗, 马晨, 郭正玉. 速度匹配算法在传递对准中的应用分析[J]. 系统工程与电子技术, 2020, 42(10): 2328-2333. DOI:10.3969/j.issn.1001-506X.2020.10.22 |
| [7] |
段晨浩, 王珏, 邓志鑫. 基于平方根 UKF 的伪卫星动态跟踪定位算法[J]. 河北科技大学学报, 2020, 41(6): 493-499. DOI:10.7535/hbkd.2020yx06003 |
| [8] |
解春明, 赵剡, 邓俊云. 一种改进的自适应平方根传递对准滤波算法[J]. 系统工程与电子技术, 2011, 33(3): 622-626. DOI:10.3969/j.issn.1001-506X.2011.03.31 |
| [9] |
WANG Zhan-qing, LI Li-hua, LIU Xin, et al. Transfer alignment of shipborne aircraft with large misalignmentbased on rotation vector error model[J]. Journal of Chinese Inertial Technology, 2016, 24(6): 723-729. |
| [10] |
宋丽君, 段中兴, 何波, 等. H∞次优滤波在角速度匹配传递对准中的应用[J]. 传感技术学报, 2017, 30(8): 1199-1203. DOI:10.3969/j.issn.1004-1699.2017.08.012 |
 2023, Vol. 45
2023, Vol. 45
