0 引　言

船舶避碰策略决定了船舶航行的安全性，传统的船舶避碰决策往往依赖于船舶工作人员的经验知识，受人为因素干扰较大，缺乏规则化和流程化的避碰决策体系。随着船舶数量和吨位的增加，海上航行交通环境越来越多变，船舶的操纵难度越来越大，仅仅依靠工作人员的经验已经无法满足复杂交通情况下的船舶避碰，因此需要进行船舶避碰决策的规范化、功能化。

本文研究船舶在多种规则约束下的实时避碰算法，通过系统分析船舶航行过程的避碰需求，建立船舶航行与会遇过程的数学模型，结合电子海图等现代化船舶导航工具^[1]，确定多规则约束下的船舶避碰策略，取得了良好效果。

1 多规则约束下的船舶实时避碰系统的整体设计

本文结合船舶导航与控制硬件设备，从船舶实时避碰的需求出发，建立一种多规则约束条件下的船舶实时避碰系统。

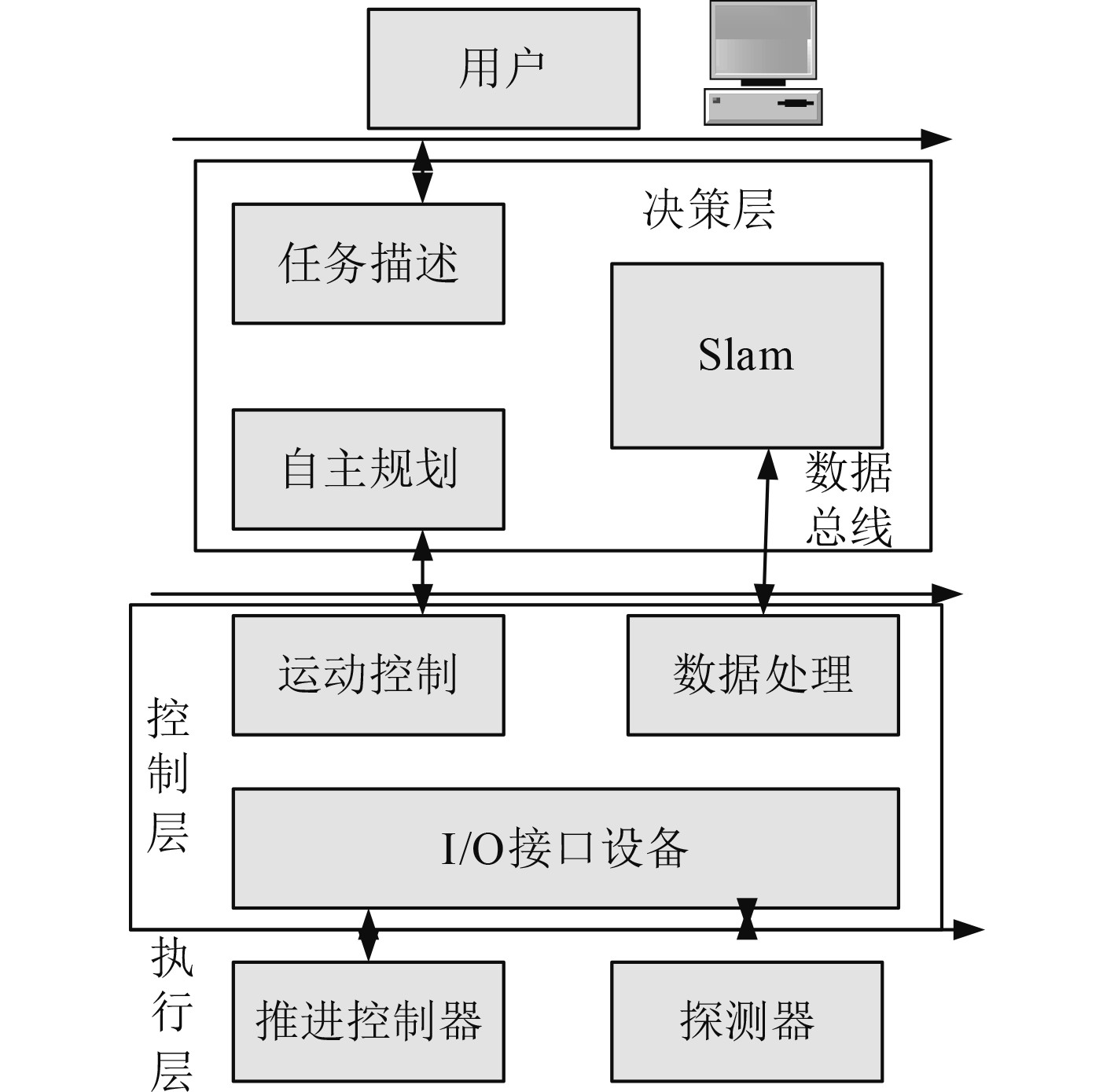
该系统按照功能模块可以分为控制层、决策层和执行层3个部分，实时避碰控制系统的用户利用局域网向3个层次结构的硬件单元发送指令信息，图1为船舶实时避碰控制系统的功能框架。

1）决策层

本文开发的船舶实时避碰系统决策层包括任务描述、自主规划、SLAM等功能模块，决策层接收来自用户的指令，是船舶避碰控制的核心^[2]。

任务描述：将来自用户或机舱的指令进行参数配置的转化，并建立任务模型，是船舶避碰控制策略制定的前提。

自主规划：该模块基于船舶的避碰控制算法，通过分析任务模型和船舶状态数据、航行环境参数，对船舶的航向进行自主的规划。

SLAM模块：该模块基于船舶自身配置的传感器单元，在控制系统中搭建避碰障碍物的分布模型，并分析本船与障碍物之间的相对分布位置。

2）控制层

控制层是实现船舶避碰的关键，主要由避碰系统的控制主机和I/O等设备组成，可以实现各种功能。

运动控制：控制层发出的控制指令由执行层接收，这些控制指令包括船舶的航行速度调节、航向改变等，从而控制船舶的运动^[3]。

数据分析：控制层的主机具有较高的数据处理能力，结合高性能主机芯片，可以对船舶传感器采集的数据进行分析、融合处理，并通过数据总线将分析后的数据传递给系统的其他单元。

设备驱动：控制层的设备驱动功能包括各类I/O端口设备、USB设备、总线设备等，保障系统数据传输的通畅。

3）执行层

船舶实时避碰系统的执行层主要包括推进控制器和探测器2个部分。

推进控制器：推进单元将来自控制层的船舶航行速度指令转化为电机的转速信号，将控制层的航行方向信号转化为舵角的控制信号，从而实现船舶的运动控制。

探测器：包括船舶的各类速度、加速度、位置传感器等，协助船舶避碰控制系统进行各类实时参数的采集。

2 多规则约束条件下的船舶实时避碰系统开发 2.1 船舶实时避碰的数学建模

影响船舶碰撞事故发生的因素很多，通常可以分为静态参数和动态参数2种。其中，静态参数主要是指船舶的长、宽、海上风浪条件等；动态参数主要是指船舶动态的航行速度、方向、会遇角度等随时间改变的参数。

在船舶实时避碰控制过程分析时，将避碰过程分解为以下环节：

1）会遇阶段

船舶以一定的会遇角度在区域内相遇，这个阶段避碰控制系统的主要工作是采集会遇过程的动态参数和静态参数。

2）避碰决策阶段

通过分析两船会遇的角度、安全距离、动态参数，对两船的避撞风险进行评估，并发送避碰控制指令。

3）执行阶段

船舶动力系统接收决策指令，进行避碰运动。

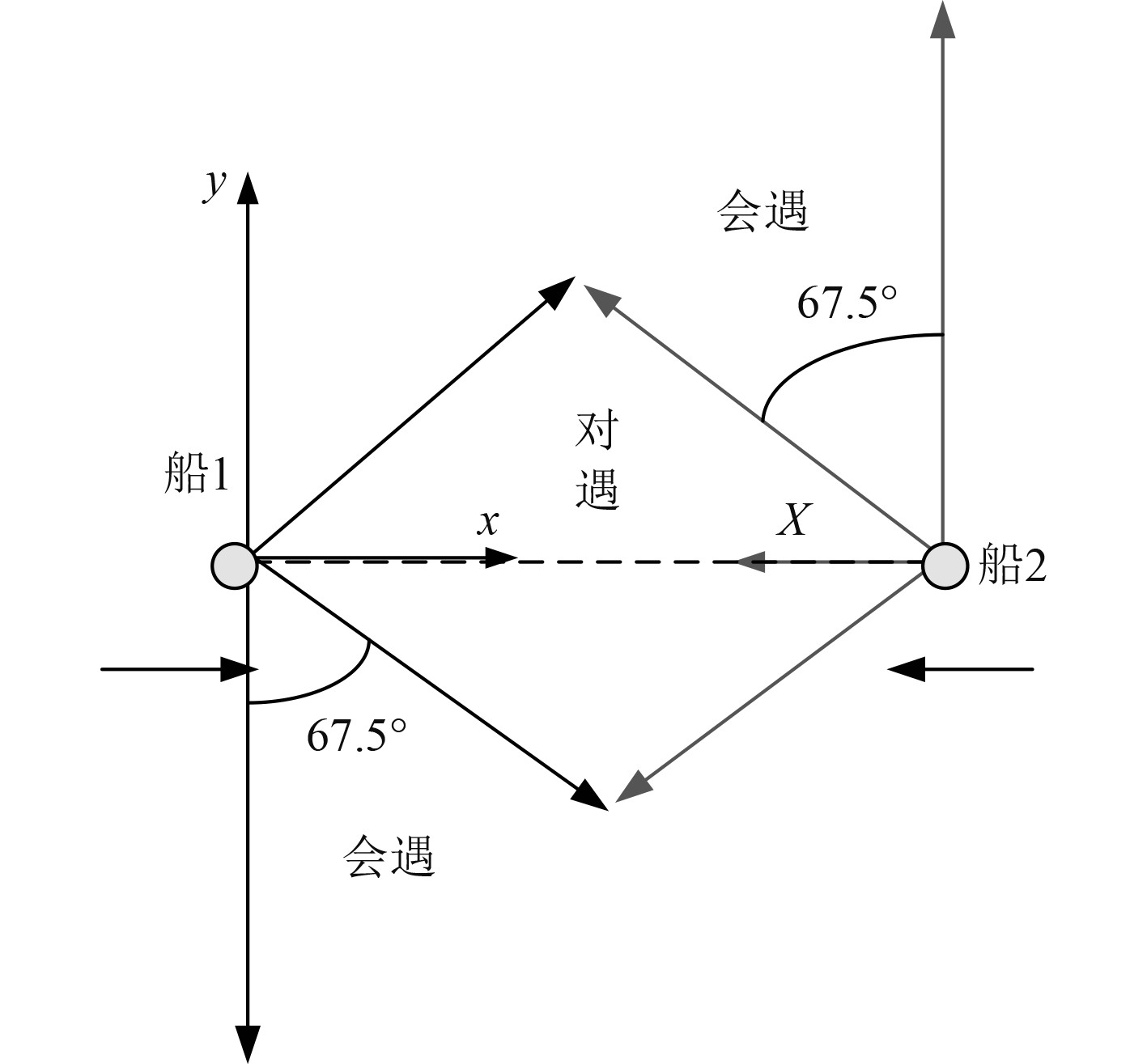
建立船舶避碰过程的数学模型如图2所示。

船舶避碰过程的参数建模如下：

1）速度模型

包括本船和会遇船舶的速度模型，分别为：

$ \left\{ {\begin{array}{*{20}{l}} {{V_{ox}} = {V_o} \cdot \sin {C_o}} ，\\ {{V_{oy}} = {V_o} \cdot \cos {C_o}} 。\end{array}} \right. $

会遇目标的速度模型为：

$ \left\{ {\begin{array}{*{20}{l}} {{V_{TX}} = {V_T} \cdot \sin {C_T}}，\\ {{V_{TY}} = {V_T} \cdot \cos {C_T}}。\end{array}} \right.$

式中： $ {V_{ox}} $ 、 $ {V_{oy}} $ 为本船在2个坐标轴方向的速度分量， $ {C_o} $ 为当前船舶航行方位角， $ {V_{TX}} $ 、 $ {V_{TY}} $ 为会遇目标在2个坐标轴方向的分量， $ {C_T} $ 为目标船舶航行方位角。

2）相对速度模型

$ \left\{ {\begin{array}{*{20}{l}} {{V_{Rx}} = {V_{TX}} - {V_{ox}}} ，\\ {{V_{Ry}} = {V_{TY}} - {V_{oy}}}。\end{array}} \right. $

根据方向矢量的计算公式，建立会遇过程的相对速度的大小为：

$ {V_R} = \sqrt {{V_{RX}}^2 + {V_{RY}}^2} \text{，} $

方向为：

$ {C_R} = \arctan \frac{{{V_{RX}}}}{{{V_{RY}}}} 。$

3）距离模型

$ {l_{ab}} = \sqrt {{{\left( {{x_T} - {x_o}} \right)}^2} + {{\left( {{y_T} - {y_o}} \right)}^2}} 。$

4）会遇角度

$ \sin \alpha = \frac{{{l_{ab}}}}{{{R_1}}} \text{，} $

$ \alpha = \arctan \frac{{\sin ({C_0} + {\alpha _1}) - \sin \theta }}{{\cos ({C_T} + {\alpha _2}) + \sqrt {\frac{1}{2}{{\sin }^2}\theta } }} 。$

式中， $ {\alpha _1}、{\alpha _2} $ 分别为本船和目标船舶的舵角。

5）安全距离和会遇时间

$ \begin{gathered} {D_C} = {l_{ab}} \times \sin \left( {{C_R} - B} \right)，\\ {T_C} = \frac{{{l_{ab}} \times \cos \left( {{C_R} - B} \right)}}{{{V_R}}}。\\ \end{gathered} $

2.2 船舶避碰系统的多规则约束条件

海上船舶的实时避碰过程并不是简单的会遇问题，在进行船舶避碰控制时还需要综合考虑多种因素，这些因素就是避碰控制系统的多规则约束条件。

1）航向保持性指标

航向保持性是指船舶避碰控制系统操纵船舶在一定航向上的直线行驶能力，可用航向偏差角度表示：

$ \Delta \theta = \max \left( {{\theta _t} - \theta } \right) \text{，} $

式中： $ {\theta _t} $ 为t时刻的航向角， $ \theta $ 为设定的航向角。

2）航向偏差平滑度

航向偏差平滑度是指一段时间内的航向偏差之和，偏差越大，变化的幅度越大，对应的平滑度指标越大，用下式计算：

$ C = \sum\limits_{T = 1}^{T = {t_s}} {} \left( {\max \left( {{\theta _t} - \theta } \right)} \right) 。$

3）路径点偏离度

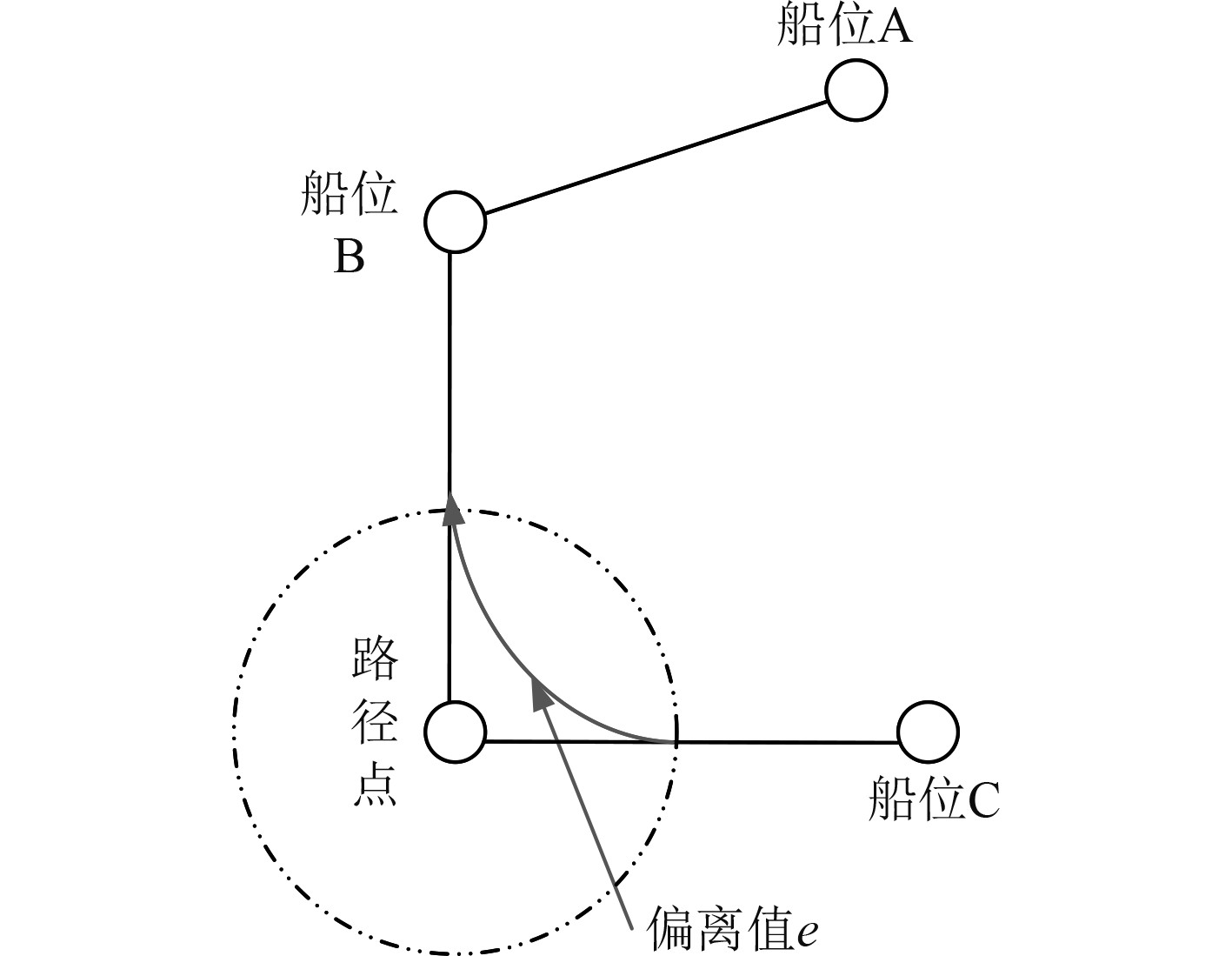
指船舶航迹偏离某路径点(拐点)的程度，当船舶经过某路径点(拐点)时^[4]，一般不会直接经过该路径点，而是以该路径点为中心，航迹沿某一半径展开，此时，路径点的偏离度就可以用该最小半径表示，如图3所示。

船舶单路径点偏离度表示为：

$ di{s_{\min }} = \min \left| {\left( {{P_t} - {p_t}} \right)} \right| \text{，} $

当路径点为n个时，多路径偏离点的计算公式为：

$ M - di{s_{\min }} = \frac{{\sum\limits \min \left| {\left( {{P_t} - {p_t}} \right)} \right|}}{n} 。$

2.3 基于电子海图的多规则船舶避碰路径建模技术

针对多规则下的船舶实时避碰控制策略，基于电子海图矢量数据，进行船舶避碰路径规划的建模与测试^[5]。

首先基于船舶与目标碰撞数学模型，建立基本的船舶避碰操作规则图如图4所示。

可知，将船舶周围海域按照避碰规则划分为如下区域：

1）F、A区域

该区域的目标障碍物存在时，本船需要采用向右避碰的措施，避开该区域的船舶或障碍物。

2）B区域

该区域障碍物存在时，不影响本船的航行状态。

3）C、D区域

该区域的目标需要分析其航行速度，如果速度大于本船，需要调整本船航行速度；如果低于本船，则无碰撞风险。

4）E区域

该区域障碍物同样不存在碰撞事故的风险。

在电子海图中设定船舶避碰控制区域为：

$ S = \{ (x,y,z(x,y))\mid (x,y) \in G\} 。$

建立二维矢量图并通过经度坐标 $ \left[ {a,b} \right] $ 和纬度坐标 $ \left[ {c,d} \right] $ 将该区域进行划分，对应的船舶和目标障碍物可用 $ {a_{ij}}\left( {{x_i},{y_i}} \right) $ 表示，对应的坐标为：

$ \begin{gathered} {x_i} = a + {(i/m)^*}(b - a)，\\ {y_i} = c + {(i/n)^*}(d - c)。\\ \end{gathered} $

然后对二维图形的节点 $ {a_{ij}}\left( {{x_i},{y_i}} \right) $ 进行插值，得到节点集合为 $ \left[ T \right] $ ，在集合 $ \left[ T \right] $ 中选取3个障碍物a、b、c的坐标为 $ A\left( {{x_1},{y_1}} \right) $ 、 $ B\left( {{x_2},{y_2}} \right) $ 、 $ C\left( {{x_3},{y_3}} \right) $ ，坐标存在关系为：

$ \begin{gathered} a{x_1} + b{x_2} + c{x_3} = {x_i}，\\ a{y_1} + b{y_2} + c{y_3} = {y_i}。\\ \end{gathered} $

最后，基于避碰策略和路径偏离度 $ \Delta \theta $ 、航向平滑度等多种约束条件，进行船舶的避碰路径规划^[6]。

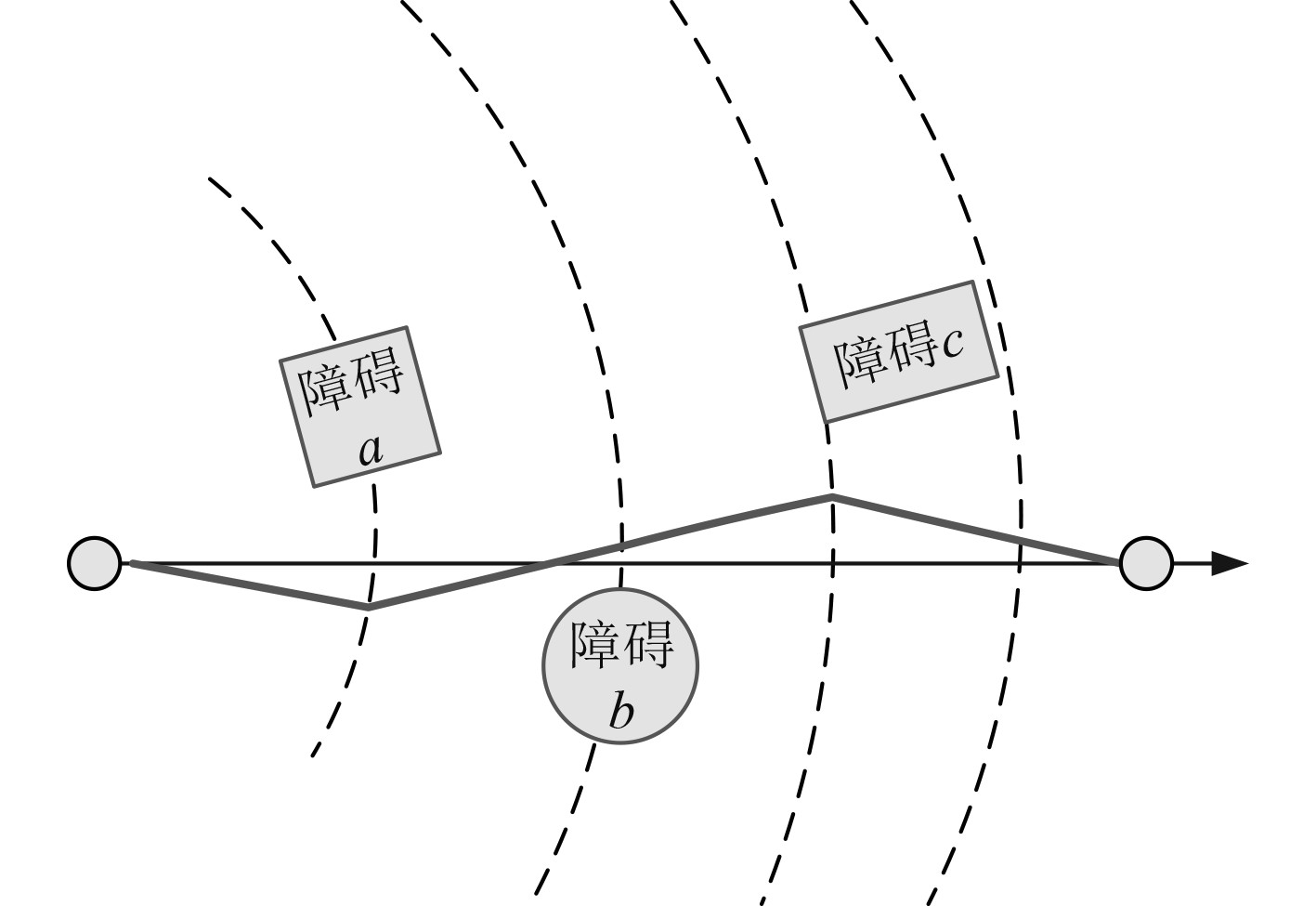
图5为电子海图中船舶多规则约束下的避碰路径规划示意图。可知，在电子海图中存在障碍物，结合船舶实时避碰算法，在电子海图规划的路径如图中轨迹线，具有较好的避碰效果。

3 结　语

海上船舶的避碰控制对于船舶航行安全性有重要意义，本文结合船舶避碰过程的数学模型，开发一种船舶实时避碰系统，并针对系统的避碰策略，在电子海图中进行避碰路径规划仿真。