在海上船舶遥感探测领域,SAR图像优异的成像能力为船舶遥感探测提供了数据支撑,使船舶遥感探测在军事和民用方面得到广泛应用。SAR目标探测和成像技术经历了较长的发展时间,目前,极化SAR图像技术由于更高的成像精度和更大的探测范围等优点,已经成为海上船舶目标SAR探测技术的主流。与此同时,极化SAR图像由于相干涉噪声等因素,需要结合后处理算法进行图像的降噪。
本文研究的核心是基于双边滤波算法进行船舶SAR图像的相干斑、高斯噪声等抑制,介绍双边滤波算法的原理,通过分析SAR雷达的噪声特性,实现船舶SAR图像的噪声过滤,对于提高合成孔径雷达SAR技术有重要的意义。
1 船舶合成孔径雷达SAR的噪声特性海上船舶合成孔径雷达的噪声来源包括雷达天线、接收器等机械部件的硬件噪声、相干涉噪声和环境干扰噪声,建立SAR图像的信噪比模型为:
| $ SNR = \frac{{{P_0}{G^2}{\beta ^2}{\delta _0}}}{{356\sigma _0^2\sqrt 2 {\text π} \sin {\theta _0}{F_0}{L_{MIN}}}}。$ |
式中:
船舶合成孔径雷达SAR图像的噪声干扰因素包括以下方面:
1)高斯噪声
高斯噪声是机械设备普遍存在的一种噪声形式,由于高斯噪声的概率密度函数满足正态分布,也把高斯噪声称之为正态噪声。
高斯噪声的概率密度函数满足下式:
| $ p(x) = \frac{1}{{\sqrt {2{\text π}} \sigma }}{e^{ - {{(x - \mu )}^2}/2{\sigma ^2}}} 。$ |
其中:
2)SAR成像的阴影特征
受限于合成孔径雷达的成像方式,SAR船舶图像存在阴影特性,具体是指当目标高度较高时,局部区域的结构会对合成孔径雷达的电磁波造成遮挡,阴影特性会造成SAR图像中目标边缘的缺失,降低成像的精度,如图1所示。

|
图 1 SAR成像的阴影特征示意图 Fig. 1 Shadow feature diagram of SAR imaging |
可知,目标B点的高度较高,导致雷达成像过程中,C点被遮挡,产生阴影特征。
2 船舶合成孔径雷达SAR图像的降噪指标为了提高SAR图像的精度,本文针对图像噪声特性设定如下降噪指标:
1)等效视数[1]
等效视数ENL是一种量化SAR图像相干涉噪声抑制水平的常用指标,定义为:
| $ ENL{\text{ = }}{{k}_\alpha }{\left( {\frac{{{\mu _0}}}{\delta }} \right)^2} 。$ |
式中:
2)无参考图像质量指标BRI
该图像质量指标最早由Mittal等于2012年提出,该指标可以衡量SAR图像的整体质量,其表达式为:
| $ \begin{split} & g\left( {x,\alpha ,{\delta ^2}} \right) = \frac{\alpha }{{2\beta (1/\alpha )}}\exp \left( { - \left( {\frac{{|x{|^2}}}{\beta }} \right)} \right)\text{,} \\ & \beta = \delta \sqrt {\Gamma (1/\alpha )/\Gamma (3/\alpha )} \text{。} \end{split} $ |
其中,
3)边缘保持指数
由于极化SAR图像包含很多边缘信息,衡量其图像降噪质量的重要指标是图像的边缘保持率,边缘保持指数EPI被定义为噪声抑制前后的图像边缘强度,用其计算式为:
| $ EPI = \frac{{\displaystyle\sum\limits_{x = 1}^n {\left| {{I_{D1}}(x) - {I_{D2}}(x)} \right|} }}{{\displaystyle\sum\limits_{x = 1}^\infty {\left| {{I_{O1}}(x) - {I_{O2}}(x)} \right|} }} 。$ |
式中:n为选定区域的像素总数,
双边滤波算法是由高斯滤波算法发展而来,且双边滤波算法弥补了高斯滤波算法的不足。
高斯滤波的基础是邻域像素的空间位置函数,根据空间位置权重进行加权平均,高斯滤波公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {h(x) = k_d^{ - 1}(x)\displaystyle\int_{ - \infty }^\infty {\displaystyle\int_{ - \infty }^\infty f } (\xi )c(\xi ,x){\rm{d}}\xi },\\ {{k_d}(x) = \displaystyle\int_{ - \infty }^\infty {\displaystyle\int_{ - \infty }^\infty c } (\xi ,x){\rm{d}}\xi } 。\end{array}} \right. $ |
式中:
双边滤波算法通过增加像素相似度权重提高图像的边缘处理效果,如下式:
| $ \begin{array}{*{20}{l}} {{h_1}(x) = k_d^{ - 1}(x)\displaystyle\int_{ - \infty }^\infty {\displaystyle\int_{ - \infty }^\infty {} } f(\xi )s(\xi ,x){\rm{d}}\xi } ,\\ {{k_{d1}}(x) = \displaystyle\int_{ - \infty }^\infty {\displaystyle\int_{ - \infty }^\infty c } (\xi ,x)s(\xi ,x){\rm{d}}\xi }。\end{array} $ |
式中:
将2种算法相组合,可以得到双边滤波算法的最终模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {h(x) = k_{}^{ - 1}(x)\displaystyle\int_{ - \infty }^\infty {\displaystyle\int_{ - \infty }^\infty f } (\xi )c(\xi ,x)s(\xi ,x){\rm{d}}\xi },\\ {k(x) = \displaystyle\int_{ - \infty }^\infty {\displaystyle\int_{ - \infty }^\infty c } (\xi ,x)c(\xi ,x){\rm{d}}\xi } 。\end{array}} \right. $ |
双边滤波算法的噪声标准差

|
图 2 双边滤波算法的噪声标准差和灰度标准差拟合曲线 Fig. 2 The fitting curve between noise standard deviation and gray standard deviation of bilateral filtering algorithm |
可知,灰度标准差随着噪声标准差的增加而呈线性增加。
3.2 基于边缘处理的极化双边滤波算法研究针对船舶的极化SAR图像降噪问题,本节在空间域和极化域内设计2个高斯核函数,通过分析像素之间的相似性进行噪声过滤。
极化SAR特征图像的降噪处理原理如图3所示。
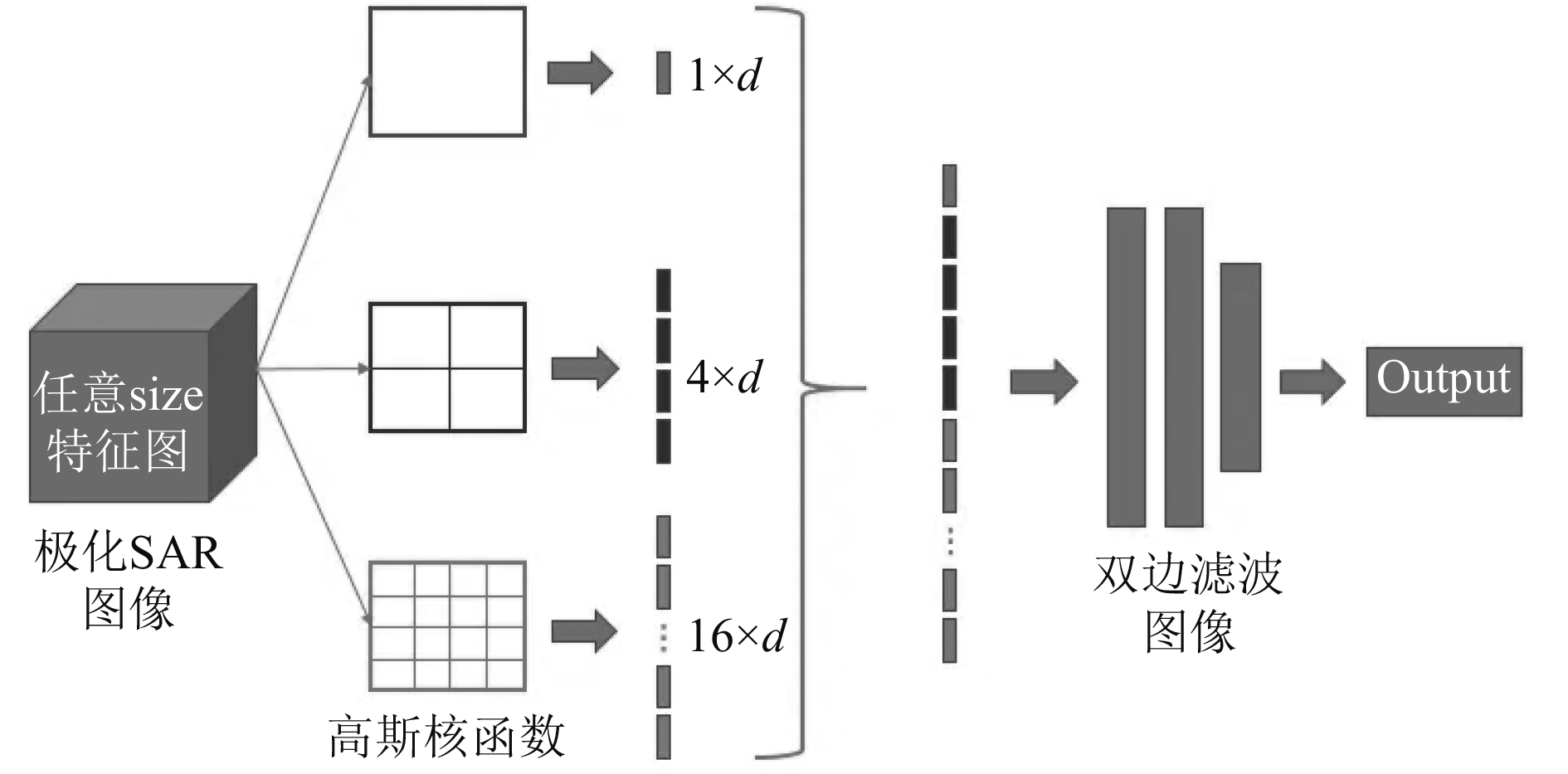
|
图 3 极化SAR特征图像的降噪处理原理图 Fig. 3 Polarization-sar feature image denoising processing principle diagram |
对于极化SAR图像的空间相似性,本文采用像素的协方差矩阵来描述,计算公式为:
| $ {\hat T_x} = \frac{1}{Z}\sum\limits_{y \in N(x)} {{w_s}} (x,y){w_p}(x,y) 。$ |
式中:
| $ {w_p} = \exp \left( { - \frac{1}{{2\sigma _p^2}}{d^2}\left( {{T_x},{T_y}} \right)} \right) 。$ |
式中:
| $ {d_{MM}}\left( {{T_x},{T_y}} \right) = \log \left[ {T_x^{ - 1/2}T_y^{ - 1/2}} \right] 。$ |
为了提高图像的降噪性能,本节采用一种迭代双边滤波算法,其算法模型为:
| $ {\hat T_x}^{n + 1} = \frac{1}{Z}\sum\limits_{y \in N(x)} {{w_s}} (x,y){w_p}(x,y){\hat T_x}^n 。$ |
其中,n为迭代次数,迭代算法流程图如图4所示。
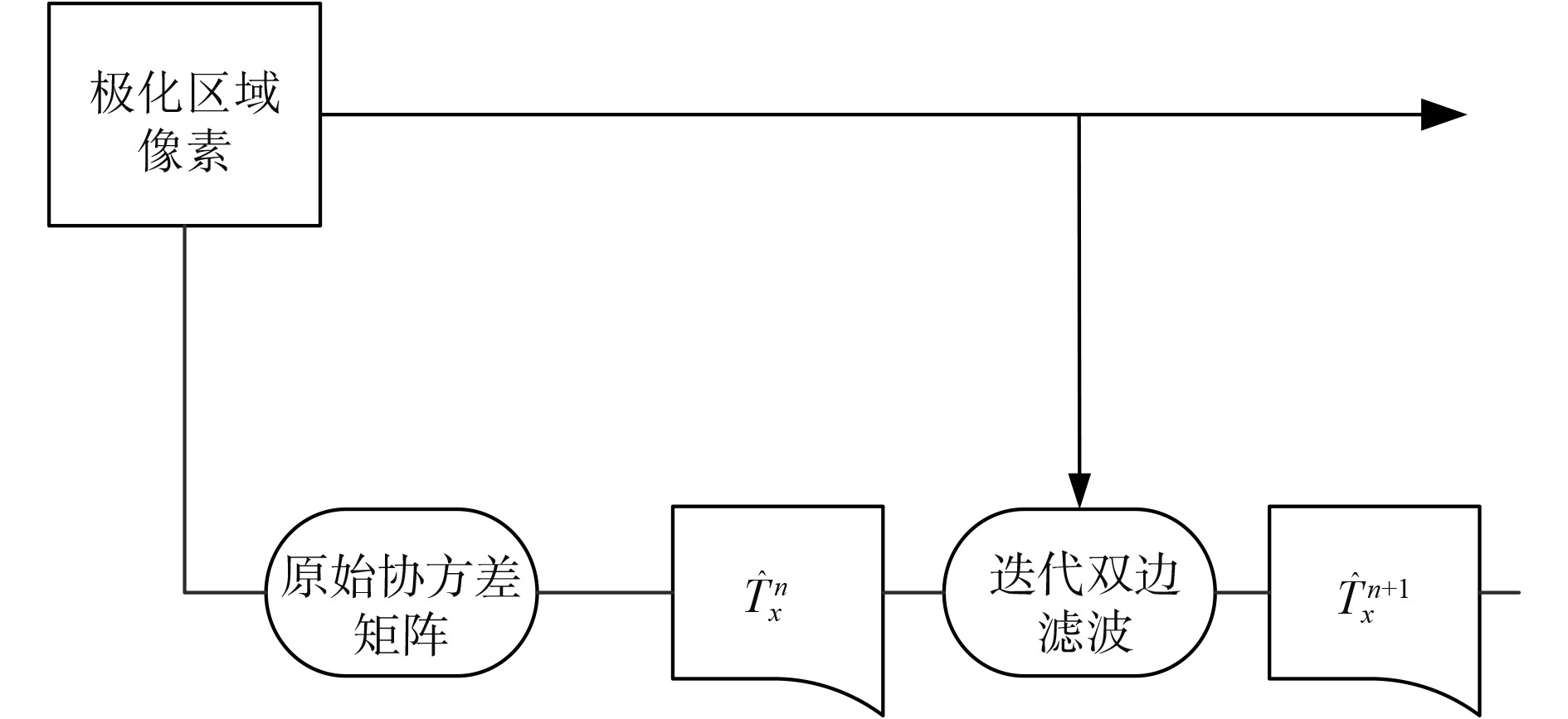
|
图 4 迭代双边滤波算法流程图 Fig. 4 Flow chart of iterative bilateral filtering algorithm |
迭代流程里极化区域的像素首先提取原始协方差矩阵,得到矩阵
采用双边滤波算法,研究船舶SAR图像混合域的噪声处理,基本原理如图5所示。

|
图 5 基于双边滤波算法的图像去噪流程图 Fig. 5 Image denoising flow chart based on bilateral filtering algorithm |
基于双边滤波算法的SAR图像去噪的关键环节包括以下内容:
1)构建PCA训练样本集[3]
为了匹配图像的边缘结构,基于双边滤波算法的图像去噪对象并不是单个像素点,而是SAR图像的某个像素区域,如图6所示。将像素区域用

|
图 6 基于双边滤波算法的SAR目标PCA样本选取 Fig. 6 Fig.6SAR target PCA sample selection based on bilateral filtering algorithm |
定义PCA样本区域图像表示为:
| $ {x_n} = x + n 。$ |
式中:x为无噪声像素,
PCA局部图像与目标像素块之间的均方误差如下式:
| $ {e_i} = \frac{1}{m}\sum\limits_{k = 1}^m {{{\left[ {x_0^n(k) - x_i^n(k)} \right]}^2}} \approx \frac{1}{m}\sum\limits_{k = 1}^m {{{\left[ {{x_0}(k) - {x_i}(k)} \right]}^2}} + 2{\sigma ^2} 。$ |
式中:
2)图像重构
结合双边滤波算法的相干矩阵,需要对含有噪声的图像像素进行重构,表示为:
| $ {\overrightarrow Y _K} = {w_k} \cdot {\overrightarrow Y _N}^k 。$ |
式中:
SAR图像重构的原理图7所示。
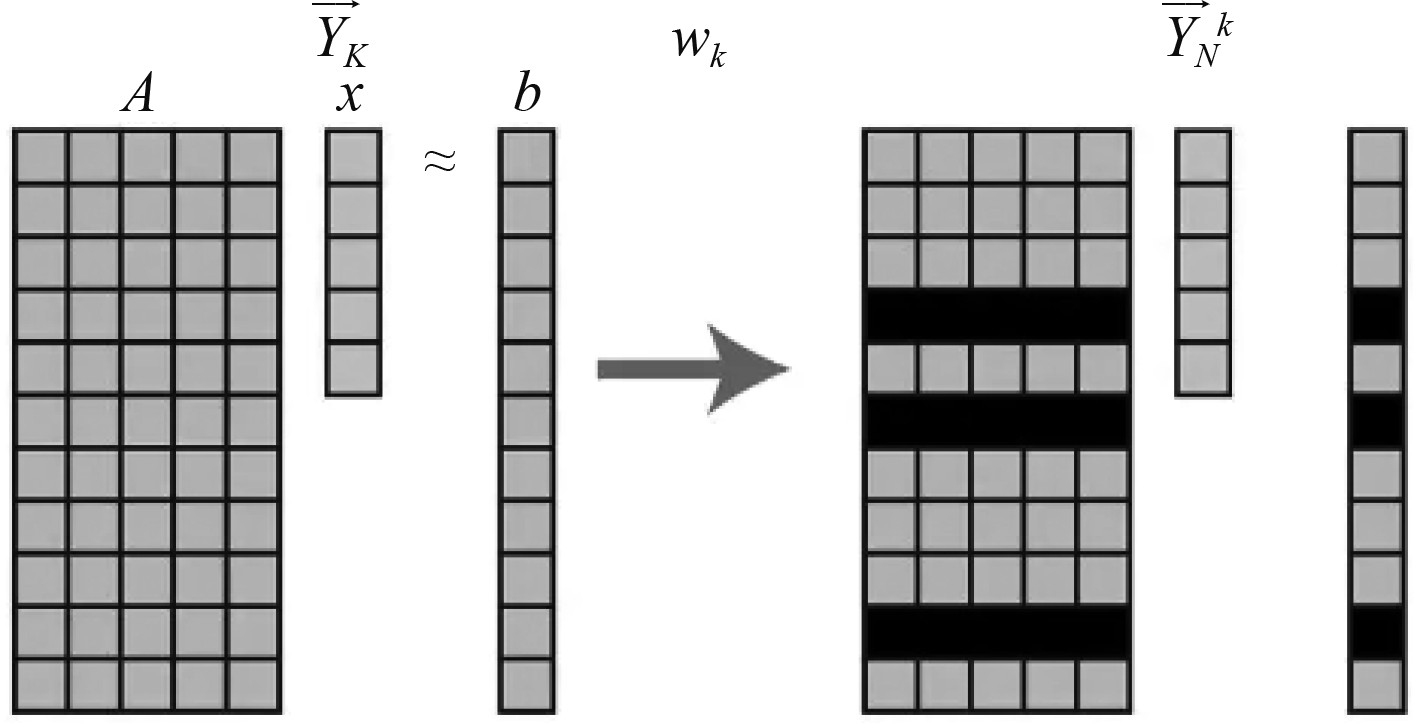
|
图 7 SAR图像重构的原理图 Fig. 7 Schematic diagram of SAR image reconstruction |
3)获取SAR去噪图像
结合实船SAR图像和VS2010图像处理平台,对基于双边滤波算法的SAR图像去噪进行测试,图8为测试结果,可见噪声抑制效果比较明显。

|
图 8 基于双边滤波算法的SAR图像去噪测试 Fig. 8 SAR image denoising test based on bilateral filtering algorithm |
本文提出一种基于双边滤波的船舶图像混合域去噪方法,详细介绍了双边滤波算法的原理和SAR图像的去噪流程。基于VS2010平台的图像降噪测试结果表明,基于双边滤波算法的图像处理具有良好的降噪效果。
| [1] |
邓冠男, 贾永鑫, 刘乙鑫. 基于自适应参数双边滤波和小波变换的图像检索方法[J]. 计算机应用与软件, 2023, 40(1): 205-209+240. DENG Guan-nan, JIA Yong-xin, LIU Yi-xin. Image retrieval method based on adaptive parameter bilateral filtering and wavelet transform[J]. Journal of Computer Applications and Software, 2023, 40(1): 205-209+240. DOI:10.3969/j.issn.1000-386x.2023.01.032 |
| [2] |
聂丰英, 侯利霞, 万里勇. 自适应双边滤波与方向梯度的红外图像增强[J]. 红外技术, 2022, 44(12): 1309-1315. NIE Feng-ying, HOU Li-xia, WAN Li-yong. Infrared image enhancement with adaptive bilateral filtering and directional gradient[J]. Infrared Technology, 2022, 44(12): 1309-1315. |
| [3] |
陈妍, 徐海黎, 邢强, 等. 结合小波变换和双边滤波的SICM图像降噪算法[J]. 电子测量技术, 2022, 45(4): 114-119. CHEN Yan, XU Hai-li, XING Qiang, et al. SICM image denoising algorithm combined with Wavelet transform and bilateral filtering[J]. Electronic Measurement Technology, 2022, 45(4): 114-119. |
 2023, Vol. 45
2023, Vol. 45
