0 引　言

永磁调速器普遍应用于舰船发电机转速控制领域中^[1]，其性能对于舰船发电机组的工作稳定性产生直接影响^[2]。在舰船运行过程中，由于不了解永磁调速器运行原理导致的发电机组故障问题时有发生^[3]，所以加强相关人员对永磁调速器的了解与掌握程度，成为提升舰船现代化管理的主要方式之一。

汤斯佳等^[4]基于调速器的运行原理构建其力—运动数学模型与流量数学模型，并对所构建模型进行仿真分析。该模型的仿真数据与实际台架测试数据之间存在较大误差，说明该模型的构建存在一定片面性。王玥等^[5]针对某型号发电机，构建发电机仿真分析，并通过仿真分析确定对调速器运行产生直接影响的参数。该模型需要进行大量计算，且计算过程较为复杂，消耗时间较长。

针对上述文献中存在的问题，研究船用永磁调速器的数学建模和仿真分析，有效提升对永磁调速器的了解与掌握程度。

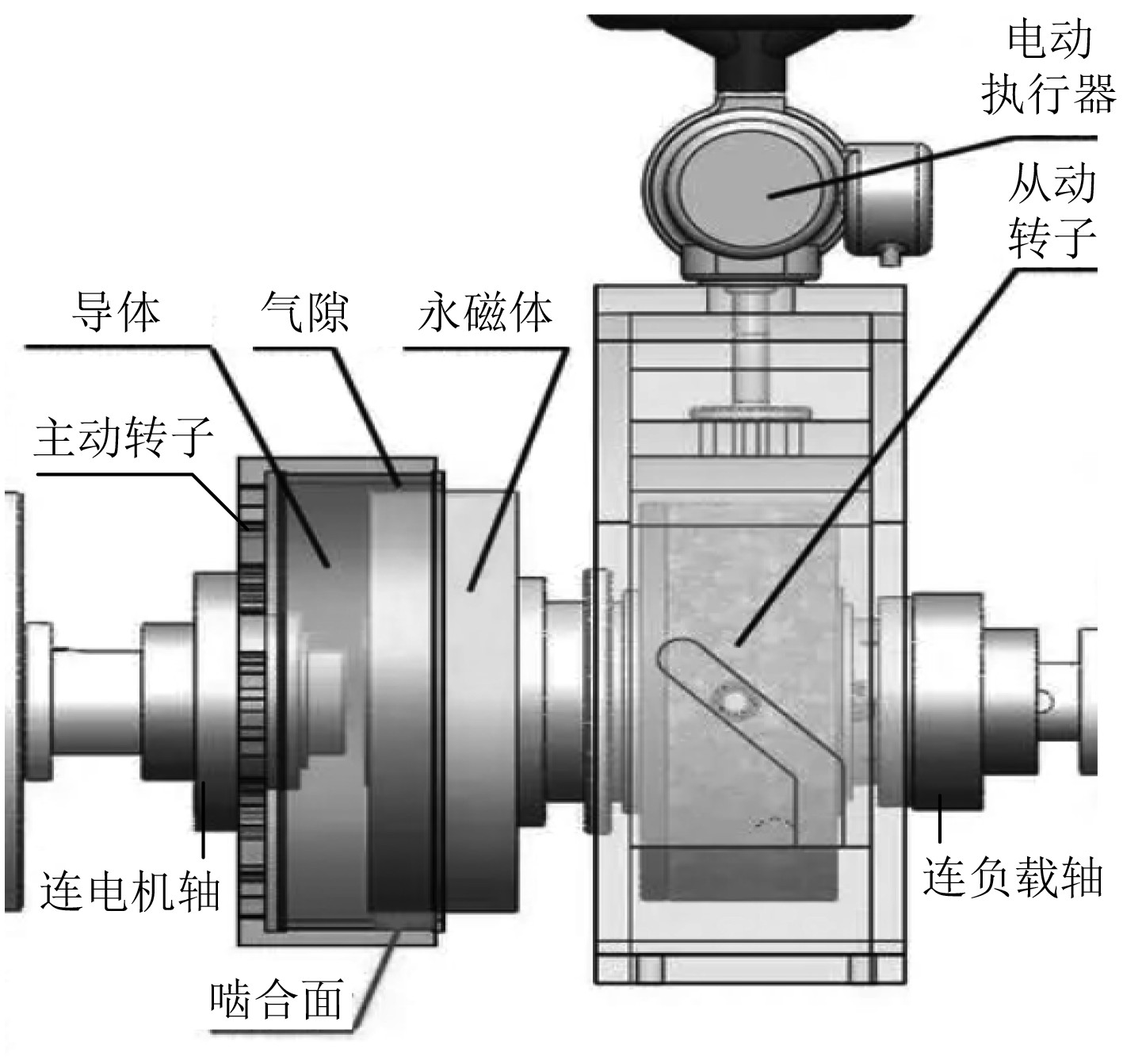
1 船用永磁调速器的数学建模 1.1 船用永磁调速器结构

图1为船用永磁调速器的大致结构框架，其中包括连电机轴、主动转子、导体、永磁体、连负载轴和从动转子等主要部分^[6]。船用永磁调速器利用导体旋转分离磁感线形成感应磁场实现转矩传输，利用永磁调速器的轴向耦合长度调整过程改变转速。电机连接主动转子，其正常运行条件下带动主动转子旋转，基于导体上形成的磁通量，永磁体产生波动生成时变的感应电流。根据楞次原理能够得到^[7]，从动转子为抵抗永磁体的波动，与导体转子保持相同的旋转方向，从导体上经过的磁通量波动越显著，导体上所形成的涡电流越显著，同时输出转矩也变得更为显著。通过输出转矩能够判断联轴器的关键度，因此构建数学模型，分析对船用永磁调速器输出转矩产生影响的参数具有重要意义。

1.2 传递转矩的数学模型

对于船用永磁调速器内的导体长度值，定义其厚度显著高于材料的趋肤深度，因此定义导体厚度的上限与下限分别为 $ + \infty $ 和0，对感应电流密度实施积分处理，获取感应电流，并以此为基础获取船用永磁调速器内导体的感应电流有效值：

$ {I_e} = \frac{1}{2} \times \frac{{\beta v{G_m}\Delta h}}{{1 + {k_b}{w_n}\Delta h}} 。$

(1)

式中： $ \beta $ 和 $ v $ 分别表示铜盘电导率和导体转子的线速度， $ {G_m} $ 和 $ \Delta h $ 分别表示导体表面的磁感应强度的径向分量和导体趋肤深度， $ {k_b} $ 和 $ {w_n} $ 分别表示比例系数和导体转子和永磁转子的相对角速度。

在导体转子相对于永磁转子进行匀速运动的条件下，定义导体轴上感应电流形成的电动势一致，由此造成导体上的感应电流依照Y轴均匀分布，可利用式（2）描述 $ {\rm{d}}j $ 微元的感应电流 $ {\rm{d}}i $ ：

$ {\rm{d}}i = \frac{{{I_e}}}{{2 {\text π} r}}{\rm{d}}j。$

(2)

式中， $ 2 {\text π} r $ 表示导体表层周长。

依照安培定律能够确定 $ {\rm{d}}i $ 的安培力 $ {\rm{d}}F $ ：

$ {\rm{d}}F = U{\rm{d}}i{\rm{d}}l 。$

(3)

式中， $ U $ 和 $ {\rm{d}}l $ 分别表示叠加磁场内气隙磁感应强度和单位长度。

根据式（3）能够得到单位转矩 $ {\rm{d}}T $ ：

$ {\rm{d}}T = r{\rm{d}}F 。$

(4)

式中， $ r $ 表示导体气隙中心处半径。

对式（4）实施积分处理能够获取次传递转矩，公式描述如下：

$ T = \frac{{r\beta vG_m^2\Delta h}}{{4{{\left( {1 + {k_b}{w_n}\Delta h} \right)}^2}}} 。$

(5)

以抑制船用永磁调速器的径向振动为目的，内、外筒导体厚度一致，且和永磁筒间距也一致，由此得到整体传递转矩：

$ T = \frac{{\left( {r_1^2 + r_2^2} \right)G_m^2\sqrt {\dfrac{{{\text π} \Delta n\beta }}{{15Np{\delta _0}{\delta _c}}}} }}{{4{{\left( {1 + {k_b}\sqrt {\dfrac{{{\text π} \Delta n}}{{15{\delta _0}{\delta _c}\beta Np}}} } \right)}^2}}}。$

(6)

式中： $ r_1^{} $ 和 $ r_2^{} $ 分别表示导体内、外筒气隙中心处半径， $ {\delta _0} $ 和 $ {\delta _0} $ 分别表示真空磁导率和铜盘相对磁导率， $ \Delta n $ 和 $ Np $ 分别表示永磁调速器的转速差和永磁转子的磁极对数。

基于式（6）能够得到，在导体转子与永磁转子间相对转速有所提升的条件下，叠加磁场内相对角频率也有所提升，基于导体感应电流提升，即造成传递转矩提升，同时也造成感应磁场提升，对永磁体形成消极影响。所以传递转矩需设定上限值。

针对式（6）进行 $ \Delta n $ 的一阶导数计算，得到：

$ \frac{{{\rm{d}}T}}{{{\rm{d}}\left( {\Delta n} \right)}} = \frac{{\left( {r_1^2 + r_2^2} \right)B_m^2\sqrt {\dfrac{{{\text π} \beta }}{{15Np{\delta _0}{\delta _c}\Delta n}}} \left( {1 + {k_b}\sqrt {\dfrac{{{\text π} \Delta n}}{{15{\delta _0}{\delta _c}\beta Np}}} } \right)}}{{16{{\left( {1 + {k_b}\sqrt {\dfrac{{{\text π} \Delta n}}{{15{\delta _0}{\delta _c}\beta Np}}} } \right)}^3}}} 。$

(7)

式中： $ {n_t} $ 表示转速临界值，在式（7）中 $\dfrac{{{\rm{d}}T}}{{{\rm{d}}\left( {\Delta n} \right)}}$ 值为0的条件下，能够确定 $ {n_t} $ 为：

$ {n_t} = \frac{{15{\delta _0}{\delta _c}\beta Np}}{{{\text π} k_b^2}} 。$

(8)

在式（7）中引入 $ {n_t} $ ，就能够确定传递转矩上限 $ {T_{\max }} $ ，公式描述如下：

$ {T_{\max }} = \frac{{\left( {r_1^2 + r_2^2} \right)\beta G_m^2}}{{16{K_b}}} 。$

(9)

1.3 传递效率的数学模型

X轴和Y轴分别表示船用永磁调速器的径向方向，Z轴为轴向方向。全部磁极形成的转矩均为单一永磁体运动形成的转矩叠加所得^[8]。

利用式（10）计算导体表层的涡流密度：

$ Q = \frac{{{\text π} nr}}{{15}}{B_n}，$

(10)

式中， $ n $ 和 $ {B_n} $ 分别表示导体转子转速和内外导体转子所受的磁感应强度。

依照导体转子内的涡流密度，确定损耗功率，计算公式如下：

$ \Delta P = {\int\limits_v {\rho \left| Q \right|} ^2}{\rm{d}}V，$

(11)

式中， $ \rho $ 表示导体材料电阻率。

利用式（12）计算船用永磁调速器传递效率：

$ \phi = \frac{{{P_2}}}{{{P_1}}} = \frac{{{n_2}}}{{{n_1}}} 。$

(12)

式中： $ {P_2} $ 和 $ {n_2} $ 分别表示输出功率和输出转速， $ {P_1} $ 和 $ {n_1} $ 分别表示输入功率和输入转速。

2 实验结果分析

本文研究船用永磁调速器的数学建模，并进行仿真分析。选取某型号永磁调速器为研究对象，基于其结构特征进行仿真，表1为研究对象的仿真参数。

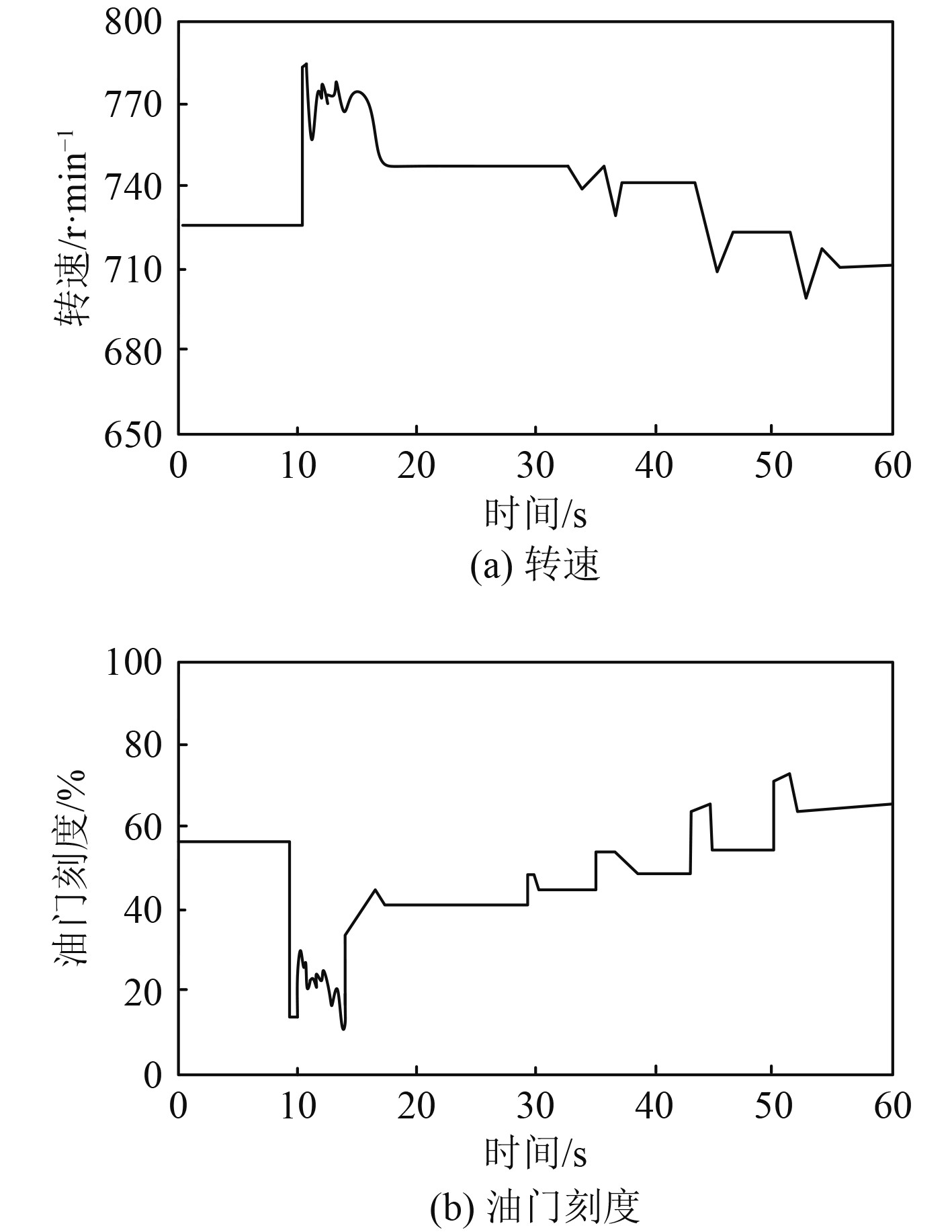
设定研究对象速度降和转速分别为40格和725 r/min，负荷从100%快速降至0%。在此条件下，转速与研究对象输出油门随响应时间的波动曲线如图2所示。分析图2可知，在负荷由100%快速下降到0%的条件下，研究对象转速快速提升到786 r/min，以保障研究对象设定转速为目的，研究对象油门输出快速下降。在经过7 s左右最终稳定在750 r/min左右；油门刻度由57格稳定在45格左右；在负荷由0提升至30%的条件下，研究对象转速由750 r/min快速下降到730 r/min，最后保持在745 r/min；在负荷由30%提升到65%的条件下，研究对象转速从745 r/min快速下降到710 r/min，最后保持在730 r/min；在负荷由65%提升到100%的条件下，研究对象转速从730 r/min快速下降到700 r/min，最后保持在715 r/min，油门刻度保持在63格。

表2为研究对象台架测试与仿真分析的稳态数据对比结果。分析表2可知，台架测试与仿真分析数据具有较高一致度，误差上限约为2%。这表明本文所构建的研究对象仿真模型既能够达到实际应用的仿真精度标准，同时还具有较高的实时性能。

3 结　语

针对当前船用永磁调速器仿真模型普遍相对简单，尚未达到相关训练与培训标准的问题，本文依照船用永磁调速器结构参数构建其数学模型，并进行仿真分析，结果显示不同工况下的台架测试与仿真分析数据误差上限约为2%，表明本文模型符合船用永磁调速器训练与培训标准，具有较高的应用价值。