Loading [MathJax]/jax/output/HTML-CSS/jax.js
  舰船科学技术  2023, Vol. 45 Issue (14): 134-140    DOI: 10.3404/j.issn.1672-7649.2023.14.025   PDF    
引用本文
郭玉琪, 毛世聪, 徐晓晗. 基于多模型广义预测控制的舰船机炉协调控制研究. 舰船科学技术, 2023, 45(14): 134-140  
GUO Yu-qi, MAO Shi-cong, XU Xiao-han. Research on coordinated control of ship based on multi-model generalized predictive control. Ship Science and Technology, 2023, 45(14): 134-140  
基于多模型广义预测控制的舰船机炉协调控制研究
郭玉琪1,2, 毛世聪2, 徐晓晗1     
1. 中国人民解放军91776部队, 北京100161;
2. 武汉理工大学, 湖北 武汉 430061
收稿日期: 2022-10-27.
作者简介: 郭玉琪(1994 -)，女，硕士，研究实习员，研究方向为舰船动力系统
摘要: 针对以机理建模为基础，采用PID策略的机炉协调系统在舰船运行期间无法平衡锅炉侧和汽机侧运行特性差异的问题，提出采用T-S模糊建模方法建立舰船协调系统模型，并基于该模型制定多模型预测控制加权策略，利用多模型广义预测控制方法设计协调控制器。仿真试验结果表明，基于多模型广义预测控制的舰船机炉协调控制系统响应速度更快、调节时间更短、稳定性更高、鲁棒性更强、综合控制效果更加优良，可有效提高蒸汽动力装置整体性能。
关键词: 舰船     机炉协调     T-S模糊建模     多模型广义预测    
Research on coordinated control of ship based on multi-model generalized predictive control
GUO Yu-qi1,2, MAO Shi-cong2, XU Xiao-han1     
1. No. 91776 Unit of PLA, Beijing 100161, China;
2. Wuhan University of Technology, Wuhan 430061, China
Abstract: Aiming at the problem that the coordinated system based on mechanism modeling uses PID strategy cannot balance the differences in the operating characteristics of the boiler side and the steam turbine side during ship operation, a T-S fuzzy modeling method was proposed to establish a ship coordination system model,and based on the model, a multi-model predictive control weighting strategy was formulated, and uses a multi-model generalized predictive control method to design a coordinated controller. The results show that the coordinated control system based on the multi-model generalized predictive control has faster response speed, shorter adjustment time, higher stability, stronger robustness, better overall control effect, and can effectively improve the overall performance of the steam power plant.
Key words: ship     coordinated control system     T-S fuzzy modeling     multi-model generalized prediction    
0 引　言

舰船蒸汽动力装置运行时，由于自身环境和各种操作需要，负荷会出现大幅度且频繁的变化[1]。常需主汽轮机在高转速区运行时突然降速，或从低转速区运行状态陡然加速到高转速，这种陡增陡降的运行方式会给主锅炉带来冲击负荷。舰用主锅炉因船舶机舱容量有限，尺寸和热容量较陆用锅炉小，需设计高效可靠的机炉协调系统来应对主汽轮机带来的负荷变化[2]。机炉协调控制系统（Coordinated Control System，CCS）是将主锅炉和主汽轮机作为一个整体来控制，包含燃油控制、风量控制、给水控制和蒸汽压力控制等[3-5]。系统热工动态过程非常复杂，具有强非线性、大时延、多变量耦合、约束多和干扰多的特点[6-8]。目前，以机理建模为基础，采用PID策略的机炉协调系统无法得到令人满意的控制效果[9-11]。为改善机炉协调控制质量，张铁军等[12]以锅炉-汽机协调系统为研究对象，利用模糊集合理论建立了该系统的非线性离散全局模糊模型，设计了一种新型的扩展状态空间预测控制器，有效地改善了整个系统的控制品质。潘晖等[13]提出一种支持向量机（SVM）的广义预测控制（GPC）建模方法和控制方法，提高了系统的稳定性和鲁棒性。

本文提出采用T-S模糊建模方法建立舰船协调系统模型，并基于该模型利用多模型广义预测控制方法设计合理的控制器[14]，以实现对协调系统快速稳定的控制，提升蒸汽动力装置整体性能。

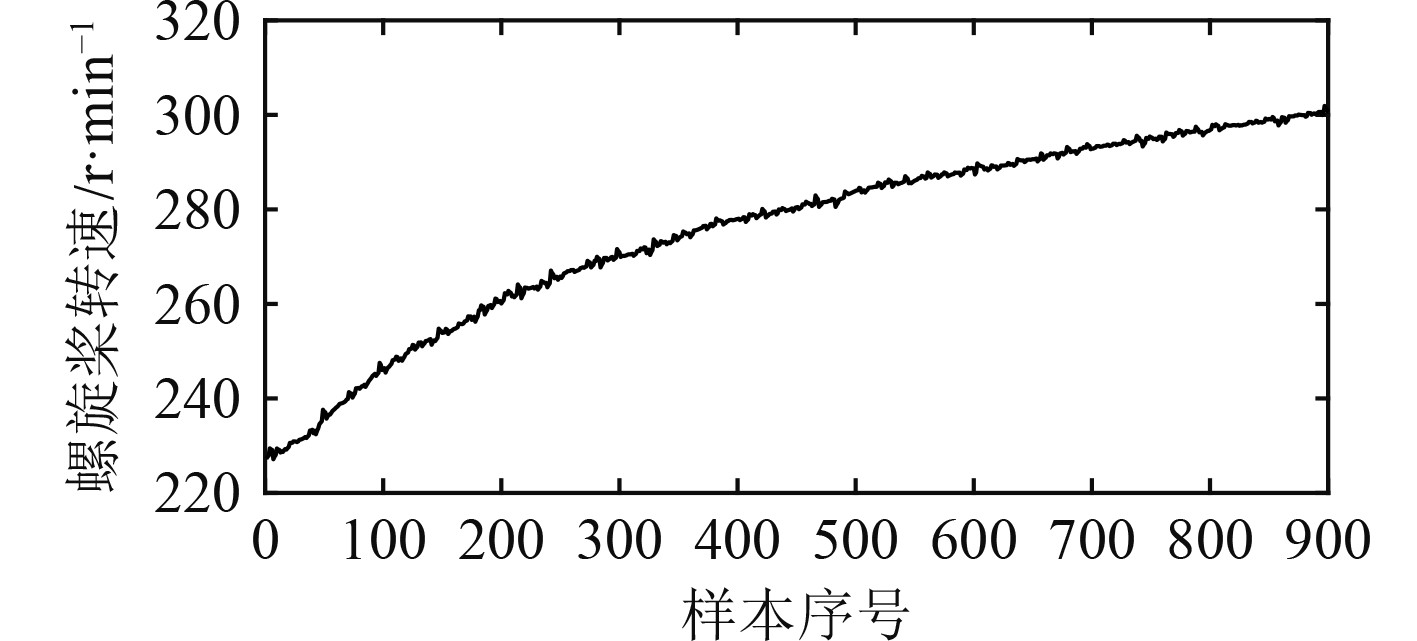
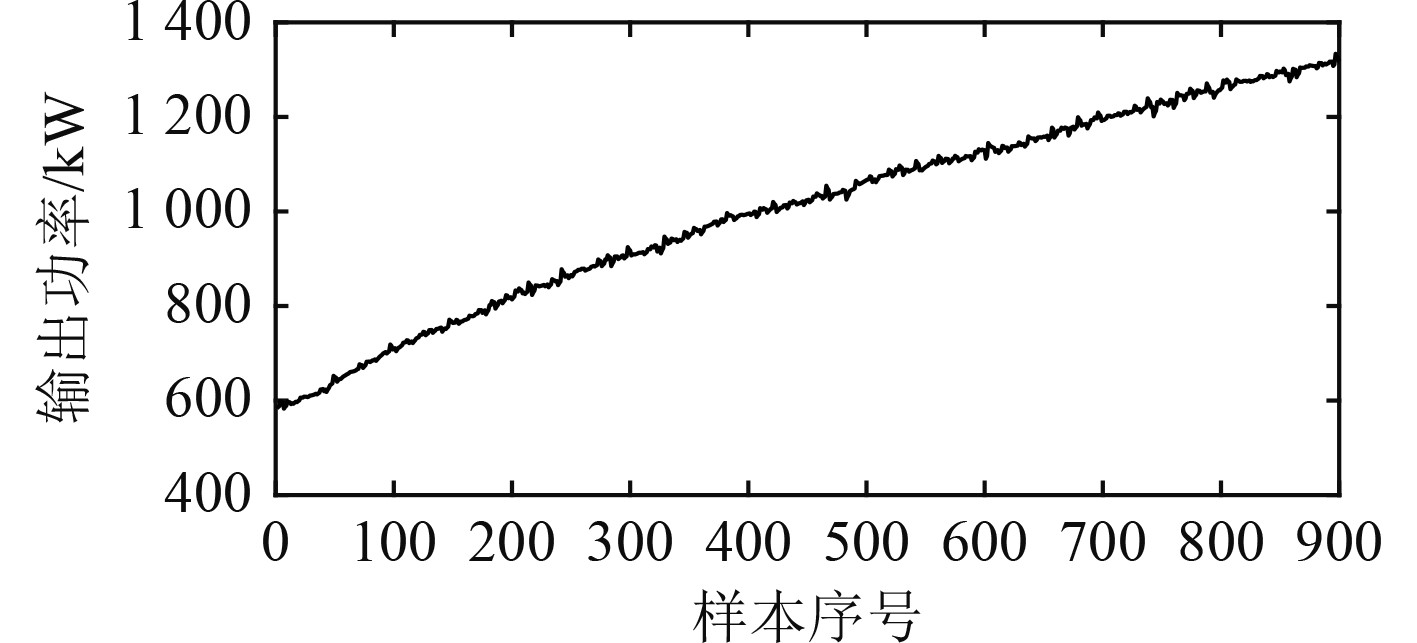
1 舰船机炉系统改进T-S模糊模型

以某训练用机组为试验对象，选择燃油量、给水量和主汽门开度作为输入变量，以螺旋桨转速、汽轮机输出功率和主蒸汽压力作为输出变量。每隔1 s采集一次现场DCS数据作为初始样本，共采集4 500组数据，为减小噪声等干扰因素对辨识效果产生的影响，在4500组数据中提取900组用于机组T-S模糊模型辨识，所提取的3个输出变量的900组数据分别如图1～图3所示。

图 1 实际机组转速数据曲线 Fig. 1 Actual unit speed data curve

图 2 实际机组输出功率数据曲线 Fig. 2 Actual unit output power data curve

图 3 实际机组主蒸汽压力数据曲线 Fig. 3 Actual unit main steam pressure data curve

为方便T-S模糊模型的搭建，按照输出变量的不同将实际机组分解成3个多输入单输出的子模型，分别为螺旋桨转速模型、输出功率模型和主蒸汽压力模型。

首先进行输入变量选择，根据启发性知识，选择燃油量、给水量和主汽门开度作为输入变量，并确定实际机组T-S模糊模型前件和后件参数中含有所有的输入变量和输出变量。由此初步确定的3个子模型结构分别为：

螺旋桨转速子模型

y1(k)=p10+p11u1(k−1)+p12u1(k−2)+p13u2(k−1)+p14u2(k−2)+p15u3(k−1)+p16y1(k−1)。

输出功率子模型

y2(k)=p20+p21u1(k−1)+p22u1(k−2)+p23u2(k−1)+p24u2(k−2)+p25u3(k−1)+p26y1(k−1)。

主蒸汽压力子模型

y3(k)=p30+p31u1(k−1)+p32u2(k−1)+p33u3(k−1)+p34u3(k−2)+p35y3(k−1)+p36y3(k−2)。

当输入变量确定后，进行输入空间模糊划分，采用FCM聚类算法进行输入空间模糊划分，设定聚类数c为5，权值指数m为2，容许误差值 ε 取 10−6 ，所求出的3个子模型聚类中心矩阵如下：

螺旋桨转速子模型

V1=[92.53 92.49 448.38 448.36 0.79 296.7167.64 67.58 424.01 423.97 0.74 257.9359.15 59.07 415.99 415.90 0.74 235.8384.35 84.32 441.35 441.30 0.75 287.1476.40 76.36 432.95 432.92 0.75 275.09]。

输出功率子模型

V2=[92.84 92.81 448.62 448.61 0.79 1264.6269.50 69.44 425.79 425.74 0.74 834.0277.83 77.79 434.40 434.35 0.75 990.7385.19 85.16 442.26 442.22 0.75 1124.7060.11 60.04 416.99 416.90 0.74 657.68]。

主蒸汽压力子模型

V3=[77.54 434.17 0.75 0.75 2.16 2.1668.95 425.24 0.74 0.74 1.84 1.8459.90 416.77 0.74 0.74 1.49 1.4985.03 441.96 0.75 0.75 2.45 2.4592.77 448.60 0.79 0.79 2.58 2.58]。

然后进行参数辨识，先进行前件参数辨识，选择高斯型隶属度函数作为辨识函数，其表达式为：

μA(x)=e−(x−a√2b)2。 (1)

式中： a 为数据集合中心； b 为数据标准差； μA(x) 为样本 x 在子集A中的隶属度。

再进行后件参数辨识，采用递推最小二乘法计算出结论参数，设定规则数为5的情况下所计算出的3个子模型的结论参数矩阵如下：

寻优后螺旋桨转速子模型

y11(k)=−67.80−0.03u1(k−1)+0.09u1(k−2)+0.02u2(k−1)+0.05u2(k−2)− 27.73u3(k−1) + 1.17y1(k−1),
y12(k)=67.47+0.43u1(k−1)−0.08u1(k−2)−0.07u2(k−1)+0.15u2(k−2)−147.02u3(k−1)+0.94y1(k−1),
y13(k)=53.79+0.04u1(k−1)−0.01u1(k−2)−0.01u2(k−1)+0.04u2(k−2)−84.64u3(k−1)+0.96y1(k−1),
y14(k)=44.85−0.03u1(k−1)+0.05u1(k−2)−0.04u2(k−1)+0.06u2(k−2)−69.84u3(k−1)+1.00y1(k−1),
y15(k)=70.44+0.09u1(k−1)−0.05u1(k−2)+0.07u2(k−1)+−0.11u2(k−2)−100.50u3(k−1)+1.07y1(k−1)。

寻优后输出功率子模型

y21(k)=−517.55−0.52u1(k−1)+1.63u1(k−2)+0.32u2(k−1)+0.93u2(k−2)−327.61u3(k−1)+1.09y2(k−1),
y22(k)=3092.02+3.06u1(k−1)−0.81u1(k−2)−3.66u2(k−1)−1.48u2(k−2)−1537.18u3(k−1)+1.10y2(k−1),
y23(k)=784.81+0.43u1(k−1)−0.40u1(k−2)+0.79u2(k−1)−0.97u2(k−2)−997.39u3(k−1)+1.04y2(k−1)，
y24(k)=616.94−0.29u1(k−1)+0.78u1(k−2)−0.66u2(k−1)+0.83u2(k−2)−956.95u3(k−1)+0.99y2(k−1)，
y25(k)=359.20+0.31u1(k−1)−0.13u1(k−2)−0.14u2(k−1)+0.29u2(k−2)−564.07u3(k−1)+0.98y2(k−1)。

寻优后主蒸汽压力子模型

y31(k)=−0.69+0.01u1(k−1)+0.01u2(k−1)−0.76u3(k−1)+0.71u3(k−2)+1.37y3(k−1)−0.41y3(k−2)，
y32(k)=−0.10+0.01u1(k−1)+0.01u2(k−1)−0.53u3(k−1)+0.57u3(k−2)+1.56y3(k−1)−0.58y3(k−2)，
y33(k)=0.01+0.01u1(k−1)+0.01u2(k−1)−0.74u3(k−1)+0.70u3(k−2)+1.40y3(k−1)−0.41y3(k−2)，
y34(k)=−0.73−0.01u1(k−1)+0.01u2(k−1)−0.45u3(k−1)+1.04u3(k−2)+1.89y3(k−1)−0.92y3(k−2)，
y35(k)=0.21+0.01u1(k−1)+0.01u2(k−1)−0.77u3(k−1)+0.61u3(k−2)+1.36y3(k−1)−0.45y3(k−2)。
2 多变量广义预测控制 2.1 多变量广义预测控制基本算法

多变量广义预测控制算法具有与单输入单输出预测控制算法一致的控制思想和设计过程，主要应用于多输入多输出系统中。以 n 输入 n 输出系统为例，所采用的CARIMA数学模型可用离散差分方程表示为：

A(z−1)Δy(t)=B(z−1)Δu(t−1)+C(z−1)ξ(t)。 (2)

其中： A(z−1) 、 B(z−1) 和 C(z−1) 是 n×n 的矩阵多项式。具体表示如下：

A(z−1)=I+A1z−1+⋯+AnAz−nA， (3)
B(z−1)=B0+B1z−1+⋯+BnBz−nB， (4)
C(z−1)=I+C1z−1+⋯+Cncz−nc。 (5)

式中： u(t) 为 n×1 维的输入向量； y(t) 表示 n×1 维的输出向量； Δ 为 n×n 对角差分矩阵，有 Δ=diag{1−z−1} ， 1−z−1 为差分算子； ξ(t) 为均值为0的白噪声向量。

选取以下函数作为性能指标：

J=N∑j=N0‖y(t+j)−yr(t+j)‖Q2+Nu∑j=1‖Δu(t+j−1)‖2λ。 (6)

式中： N0 为最小预测时域，通常情况下取 N0=1 ； N 为最大预测时域； Nu 为控制时域。 Δu(t+j)=0 ， j=Nu，⋯N ，为在 Nu 步后控制量不再发生变化。 ‖x‖2λ=xTλx ， ‖x‖2Q=xTQx ，其中 λ 和 Q 是 n×n 对角矩阵，都具有控制加权的作用，分别为 λ=diag(λ1，⋯，λn) 和 Q=diag(Q1，⋯，Qn) 。 yr(t) 是n×1维有界的设定值向量。

在 n×1 维 yr(t) 中含有 n 个设定值，每一个设定值对应一个输出变量，对于绝大多数的工业生产，采用的是恒值控制，所以一般将这 n 个值设定为常值。令第一个输出变量的设定值表达式为 y1r(t+j) ， j=1，2，⋯ ，所对应的设定常值为 y1r ，当前时刻的输出为 y1(t) ，则有如下一阶滤波方程：

{y1r(t)=y1(t)，y1r(t+j)=αy1r(t+j−1)+(1−α)y1r。 (7)

式中： α 为柔化系数，主要是用来平衡控制中的快速性和鲁棒性。较小 α 值的控制系统具有更快的跟踪速度，但鲁棒性较差。反之， α 值较大会使系统具有更好的鲁棒性，但跟踪速度会下降。因此，在选择 α 值时应当综合考虑。

为方便建立预测模型，引入以下矩阵多项式方程，该矩阵多项式方式是由多个Diophantine方程组成：

I=Ej(z−1)A(z−1)Δ+z−jFj(z−1)， (8)
Ej(z−1)B(z−1)=Gj(z−1)+z−jHj(z−1)。 (9)

式中： j=1，⋯N ，并且有

Ej(z−1)=E0+E1(z−1)+⋯+Ej−1z−j+1， (10)
Fj(z−1)=Fj0+Fj1(z−1)+⋯+FjnAz−nA， (11)
Gj(z−1)=G0+G1(z−1)+⋯+Gj−1z−j+1， (12)
Hj(z−1)=Hj0+Hj1(z−1)+⋯+HjnB−1z−nB+1。 (13)

联立式(2)、式(7)和式(8)可得：

y(t+j)=Gj(z−1)Δu(t+j−1)+Fj(z−1)y(t)+Hj(z−1)Δu(t−1)。 (14)

将上式用向量形式表示如下：

y=Gu+F(z−1)y(t)+H(z−1)Δu(t−1)。 (15)

其中：

y=[y(t+1)T,⋯,y(t+N)T]T， (16)
u=[Δu(t)T,⋯,Δu(t+Nu−1)T]T， (17)
F(z−1)=[F1(z−1)T,⋯,FN(z−1)T]T， (18)
H(z−1)=[H1(z−1)T,⋯,HN(z−1)T]T， (19)
G=[G0000G1G000⋮⋮⋮⋮GNu−1GNu−2⋯G0GN−1GN−2⋯GN−Nu]N1n×Nun。 (20)

将设定参考轨迹定义如下：

yr=[yr(t+1)T,⋯,yr(t+N)T]T。 (21)

于是可将式(5)改写为：

J=‖y−yr‖2+‖u‖2Λ， (22)

式中， Λ=diag{λ} 。

把式(14)代入到式(21)，并使 J 对 u 求导，当 J 取得最小值时有：

u=(GTQG+Λ)−1GTQ[yr−F(z−1)y(t)−H(z−1)Δu(t−1)]。 (23)

把 (GTG+Λ)−1GT 的前 n 行写作：

PT=[P1,⋯,PN]。 (24)

定义：

P(z−1)=PN+PN−1z−1+⋯+P1z−N+1， (25)

式中， Pi(i=1,2,⋯,N) 为 n×n 矩阵。

根据式(22)～式(24)，可得广义预测控制律为：

Δu(t)=PT[yr−F(z−1)y(t)−H(z−1)Δu(t−1)]=P(z−1)yr(t+N)−α(z−1)y(t)−β(z−1)Δu(t−1)。 (26)

其中 α(z−1) 和 β(z−1) 为参数矩阵多项式，分别为：

α(z−1)=N∑j=1PjFj(z−1)， (27)
β(z−1)=N∑j=1PjHj(z−1)。 (28)
2.2 多模型预测控制加权策略

由于所搭建机组模型包含多个局部线性子模型，因此，需将多个子模型进行合理的加权以实现更优的控制。考虑到本文研究对象需在不同工况下切换，为避免出现模型加权得到的整体模型与实际偏差过大的问题，采用基于控制器加权的预测控制方法设计2个系统控制器。

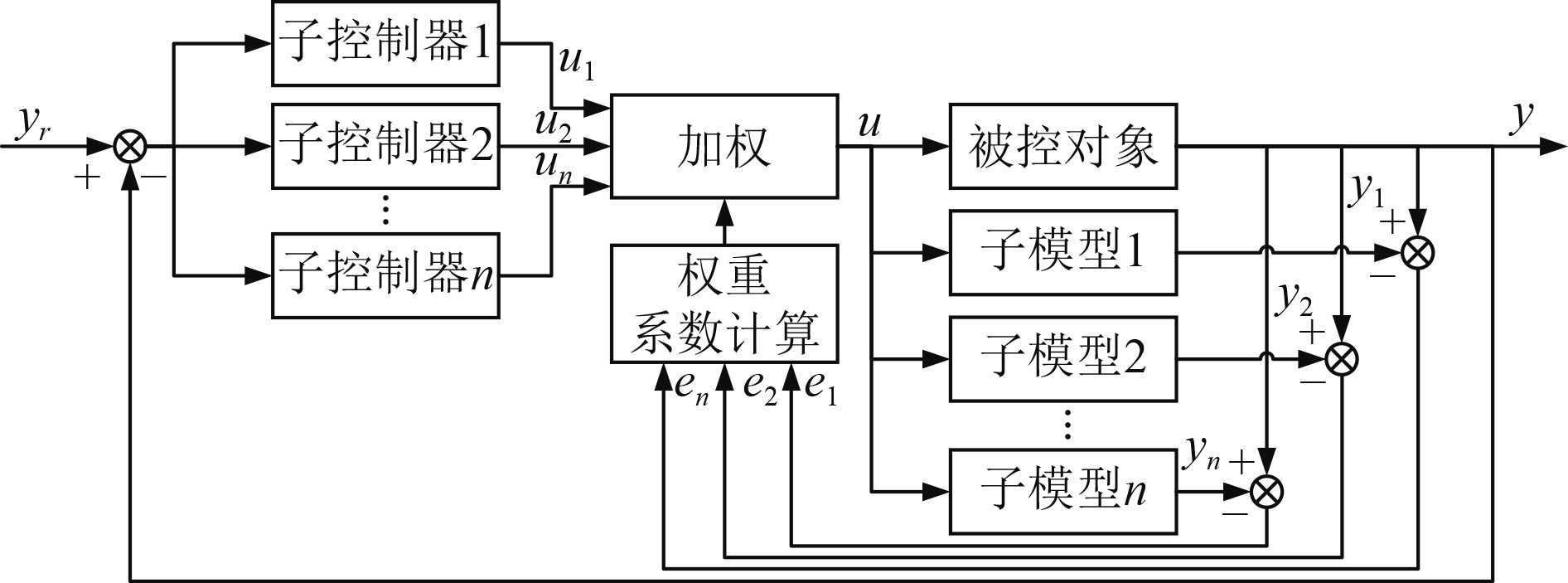
基于控制器加权方法的基本原理是分别对所建立的多个子模型设计对应的控制器，再根据不同时刻各子模型输出与实际输出的接近程度，计算出该模型对应控制器输出占总控制器输出的权重系数。随着时间的变化，权重系数也会不断发生改变，从而使总控制器输出合理，以满足控制的快速性和稳定性。基于控制器加权策略的原理如图4所示。

图 4 基于控制器加权的预测控制策略原理 Fig. 4 Principle of predictive control strategy based on controller weighting

假定某系统具有 n 个子模型，且每一个子模型含有 m 个输出变量，在 k 时刻的综合加权系数计算步骤如下：

先计算每一个子模型在 k 时刻的输出误差平方和：

εki=m∑j=1ηj(ykj−yrkj)2。 (29)

由式（28）得到该时刻各子模型的高斯隶属度为：

μki=exp(−12εki/β2)。 (30)

由此可得到第 i 个子模型控制器的权重系数为：

vki=μki/n∑i=1μki。 (31)

则 k 时刻所需要的总控制器输出：

uk=n∑i=1vkiuki。 (32)

式中： εki 为 k 时刻第 i 个子模型的输出误差平方和，其中， k=0,1,2,⋯ ， i = 1,2,⋯,n ； ykj(j=1,2,⋯,m) 为第 i 个子模型 k 时刻的第 j 个变量输出值； yrkj(j=1,2,⋯,m) 为子模型 k 时刻的第 j 个变量设定值； ηj(j=1,2,⋯,m) 为第 j 个输出变量的加权系数； μki 为 k 时刻第 i 个子模型的高斯隶属度； β 为常数，用来控制隶属度函数的分辨率，本文取0.3； uki 为 k 时刻第 i 个子模型控制器的输出。

3 仿真结果分析

为了验证基于多模型广义预测控制的舰船机炉协调控制有效性，本文设计单模型广义预测控制进行仿真对比，选择组成的5个CARIMA子模型中的第1个模型进行对照试验，并模拟阶跃扰动过程和变工况过程。表1为预测控制算法设定参数值。

表 1 实际机组中预测控制算法设定参数值 Tab.1 Parameter value set by predictive control algorithm in actual unit

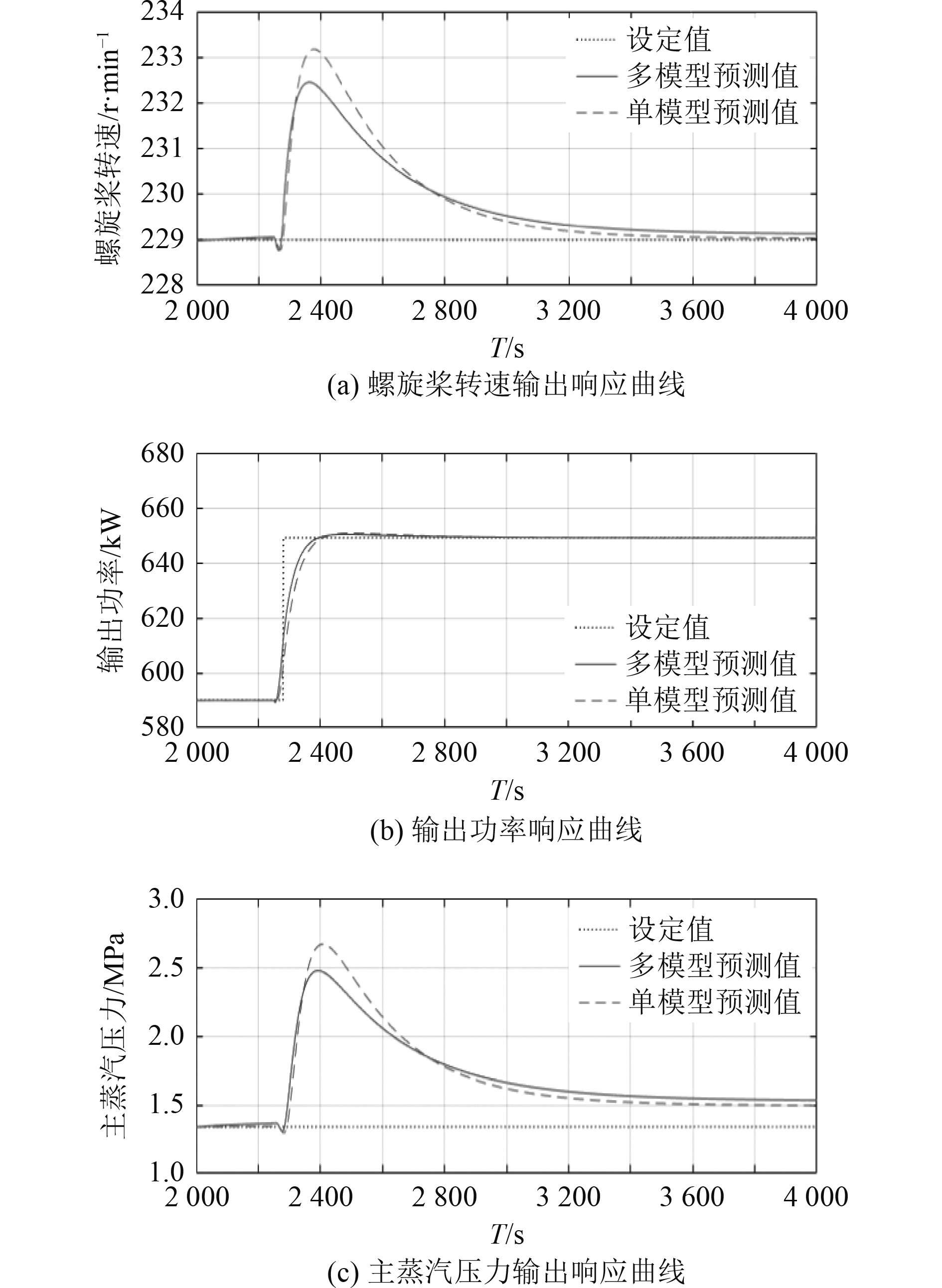
首先进行输出功率阶跃扰动试验，以45%工况点为初始工况点，待机组平稳运行在45%工况点后，在2800 s将功率设定值从590 kW阶跃至992.25 kW。在该试验中，预测控制的输出、输入响应曲线分别如图5和图6所示。

图 5 实际机组预测控制输出响应曲线 Fig. 5 Actual unit predictive control output response curve

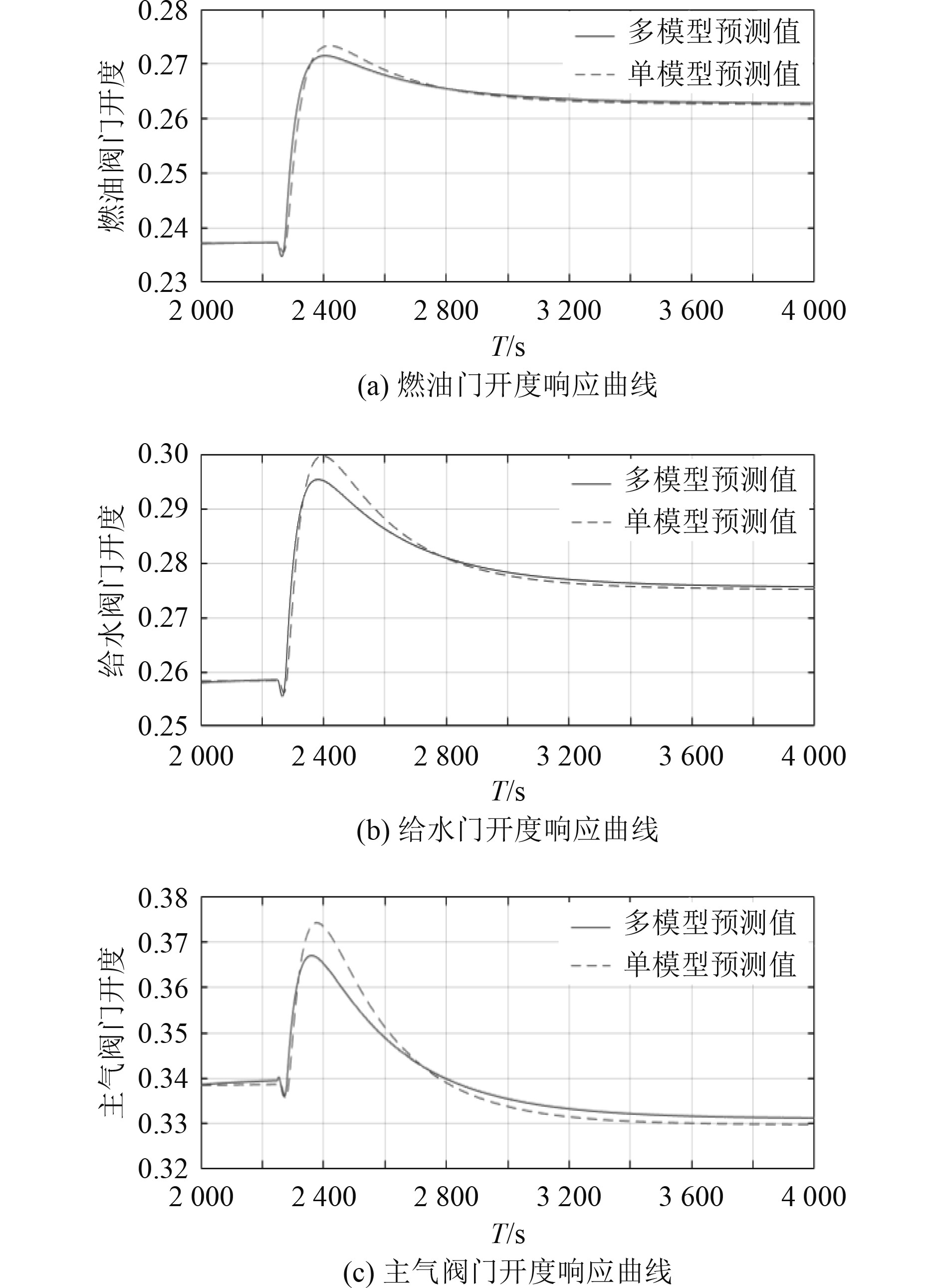
图 6 实际机组预测控制输入响应曲线 Fig. 6 Actual unit predictive control input response curve

可知，在输出功率发生阶跃扰动时，螺旋桨转速和主蒸汽压力会在短时间内小幅度下降，然后在燃油阀门、给水阀门以及主汽阀门开度不断调节的过程中先升高再下降，最后回到设定值附近。通过计算各条曲线可得，在多模型预测控制下，输出功率从开始发生变化到最终稳定的时长为93 s，而单模型预测控制下的对应时长为115 s，比前者长22 s。同时，前者作用下的转速和主蒸汽压力在调节过程中的峰值分别为232.5 r/min和2.474 MPa，比后者的相应变量峰值低0.8 r/min和0.197 MPa。在3个阀门开度的变化上，前者比后者的开度变化范围分别低0.0018、0.0049和0.0084。

再进行变工况试验，以45%工况点为初始工况点，从45%工况缓慢增加至75%工况，再缓慢下降到45%工况。该试验中，当t=2280 s时，螺旋桨转速设定值先以0.3352 （r/min）/s从229 r/min缓慢升至250.9 r/min，输出功率设定值先以0.01825 kW/s从590 kW升至992.25 kW，主蒸汽压力设定值则以 6.92×10−4 MPa/s从1.34 MPa升至2.17 MPa。待工况稳定，在t=4280 s时，螺旋桨转速设定值以0.3352 （r/min）/s从250.9 r/min缓慢降至229 r/min，输出功率设定值以0.01825 kW/s从992.25 kW降至590 kW，主蒸汽压力设定值以 6.92×10−4 MPa/s从2.17 MPa降至1.34 MPa。图7和图8分别为实际机组在变工况时的预测控制输出、输入响应曲线。

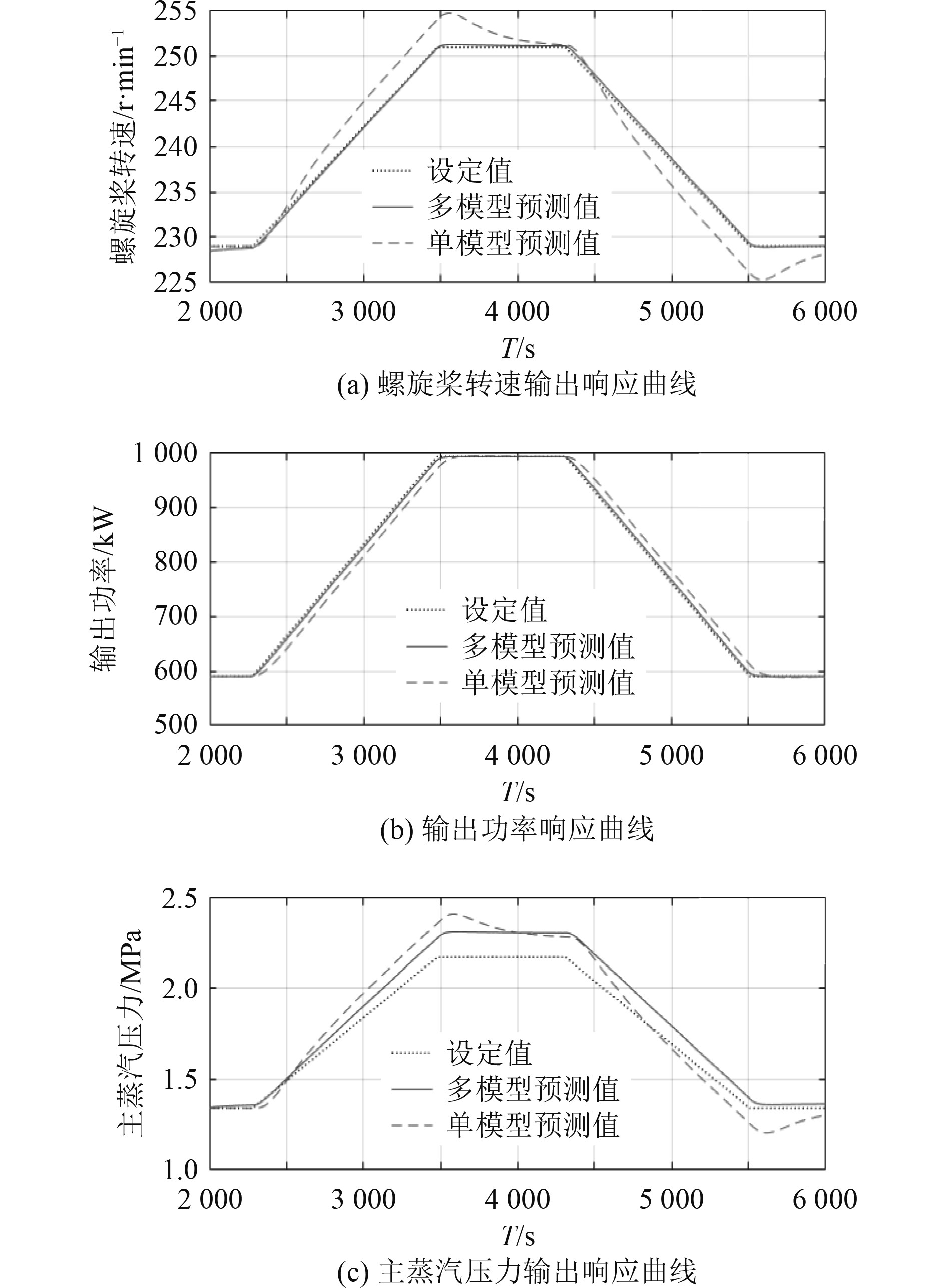
图 7 实际机组预测控制输出响应曲线 Fig. 7 Actual unit predictive control output response curve

图 8 实际机组预测控制输入响应曲线 Fig. 8 Actual unit predictive control input response curve

可以看出，多模型预测控制方法能使机组的3个输出变量平稳且快速的跟踪设定值的变化，而单模型预测控制方式在螺旋桨转速和主蒸汽压力的调节中会产生较大的波动。经计算可得，前者作用下的3个输出变量均无超调，而后者调节过程中，转速最高值比设定值高4.6 r/min，最低值比设定值低3.7 r/min，压力最高值比设定值高0.234 MPa，最低值比设定值低0.135 MPa。同时，单模型预测控制方式中的3个阀门开度变化幅度也比多模型控制方法中的对应值更大。

4 结　语

针对舰船机炉协调系统锅炉侧和汽机侧运行特性差异显著、综合调节困难的问题，本文根据某型训练用机组输入输出数据建立了舰船机炉系统T-S模糊模型，并采用多模型广义预测控制算法设计了协调控制器。经验证，与单模型预测控制方法相比，该控制策略提高了响应速度，缩短了调节时间，减少了调节过程中的波动量，使输出更加平稳，有效提升蒸汽动力装置的整体性能。

参考文献
[1]
张倩. 船用动力装置机炉协调控制系统优化设计[D]. 哈尔滨: 哈尔滨工程大学, 2009.
[2]
任立永. 船舶动力装置机炉协调控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
[3]
丁春辉. 基于神经内模控制算法的船舶蒸汽动力装置协调控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.
[4]
谢春甫. 提升火电机组灵活性的机炉协调控制优化研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
[5]
张兴华. 锅炉-汽轮机机炉协调控制系统在火电厂中的应用[J]. 江西建材, 2016(17): 221+225.
ZHANG Xinghua. Application of boiler turbine boiler coordinated control system in thermal power plants [J]. Jiangxi Building Materials, 2016(17):221+225.
[6]
张帆. 多目标非线性预测控制及其在机炉协调优化控制中的应用研究[D]. 南京: 东南大学, 2017.
[7]
柳善建. 基于仿射模糊模型的复杂热工过程跟踪控制方法研究[D]. 南京: 东南大学, 2015.
[8]
袁桂丽, 陆斯悦. 单元机组协调控制系统综合性能评价[J]. 动力工程学报, 2017, 37(11): 895−902.
YUAN Guili, LU Siyue. Comprehensive performance evaluation of coordinated control system for unit [J]. Journal of Power Engineering, 2017, 37(11): 895−902.
[9]
阮浩. 多模型控制研究及其在机炉协调系统中的应用[D]. 南京: 东南大学, 2016.
[10]
吴国垣, 李东海, 薛亚丽. 机炉协调控制的分散PID整定[J]. 清华大学学报(自然科学版), 2004, 44(2): 262−265.
WU Guoyuan, LI Donghai, XUE Yali. Decentralized PID tuning for coordinated control of machines and boilers [J]. Journal of Tsinghua University (natural science edition), 2004, 44(2): 262−265.
[11]
张帆, 吴啸, 沈炯. 超超临界机组机炉协调系统的模糊抗扰动预测控制(英文)[J]. 东南大学学报: 2017, 33(01): 53−58.
ZHANG Fan, WU Xiao, SHEN Jiong. Fuzzy disturbance rejection predictive control of ultra-supercritical once-through boiler-turbine unit [J].Journal of Southeast University, 2017, 33(1): 53−58.
[12]
张铁军, 吕剑虹, 华志刚. 机炉协调系统的模糊增益调度预测控制[J]. 中国电机工程学报, 2005(4): 160−167.
ZHANG Tiejun, LV Jianhong, HUA Zhigang. Fuzzy gain scheduling predictive control for machine furnace coordination system [J]. Proceeding of the CSEE, 2005(4): 160−167.
[13]
潘晖, 张冀, 缪伟彬. 面向广义预测控制的协调控制系统建模与控制[J]. 上海电力学院学报, 2019, 35(5): 465−471.
PAN Hui, ZHANG Yi, MIU Weibin. Modeling and control of coordinated control systems for generalized predictive control [J]. Journal of Shanghai University of Electric Power, 2019, 35(5): 456−471.
[14]
杨优生, 王东风, 智丹. 基于动态模糊神经网络的机炉协调系统建模[J]. 电力科学与工程, 2017, 33(7): 58−63.
YANG Yousheng, WANG Dongfeng, ZHI Dan. Modeling of machine furnace coordination system based on dynamic fuzzy neural network [J]. Electric Power Science and Engineering, 2017, 33(7): 58−63.
基于多模型广义预测控制的舰船机炉协调控制研究
郭玉琪, 毛世聪, 徐晓晗