船用柴油发动机是船舶的动力核心,为了提高对船舶柴油发动机的实时监测,行业内有针对性的开发了各种在线监测技术,如温度监测、振动监测、速度与加速度监测等。其中,基于振动信号的船舶柴油机监测能够快速和准确的对柴油机故障进行定位,是最行之有效的监测手段。
本文针对柴油机发动机冲击故障类型建立基于振动分析的监测系统,分析船用柴油发动机冲击载荷的激励来源,建立冲击激励的数学模型和能量模型,包括发动机、主轴系等部件,为船舶柴油发动机振动监测系统的设计确定输入信号。基于专家系统知识库和数据库技术,设计和开发针对柴油发动机的冲击故障能量采集传感器,基于传感器设计柴油发动机的冲击故障监测系统。通过搭建试验品,进行冲击故障监测系统的模拟测试,验证了监测系统的各项性能。
1 船用柴油发动机的冲击激励来源与建模船用柴油发动机的结构复杂,在柴油发动机的工作过程中,冲击激励会导致部件载荷增大,甚至导致精密部件的失效,船用柴油发动机的工作环境非常恶劣,其冲击激励主要来源于以下方面:
1)直接冲击激励
主要是指柴油机气缸内燃烧产生的气体冲击和曲柄、连杆的惯性力冲击,通常内部的气体力激励和惯性力激励频带较宽,冲击载荷较大。
2)间接冲击激励
包括柴油发动机进气与排气行程中产生的基座振动激励,这类激励是由于气体力、惯性力激励的作用下间接产生的,归类于间接冲击激励。
3)其他激励源
包括海浪冲击载荷、机械碰撞等。
本文建立船用柴油发动机系统的动力学等效模型如图1所示。

|
图 1 船用柴油发动机系统的动力学等效模型 Fig. 1 Dynamic equivalent model of marine diesel engine system |
根据动力学原理,建立柴油发动机系统的动能方程为:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial {E_1}}}{{\partial s}}} \right) - \frac{{\partial {E_2}}}{{\partial s}} + \frac{{\partial {E_o}}}{{\partial s}} = 0 \text{,} $ | (1) |
其中,
| $ {E_1} = \frac{1}{2}m{\gamma ^3}{\alpha ^2}。$ | (2) |
式中:
假设在冲击载荷作用下,柴油发动机的振动位移为
| $ \frac{{{M_1}}}{{{e^{jwt}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\rm{d}}}{{{\rm{d}}t}}x\left( t \right) + \frac{{{M_2}}}{{{e^{jwt}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}\dot x\left( t \right) + \frac{{{M_3}}}{{{e^{jwt}}}}x\left( t \right) = \sum\limits_{}^{} {{F_i}} 。$ | (3) |
式中:
动力学分析中,船用柴油发动机的冲击作用力矩如下式:
| $ \left\{\begin{aligned} & {T}_{1}={F}_{i}\cdot \left[1-\left(\frac{{F}_{i}}{s}\right)\right]\cdot \frac{{d}_{1}{}^{2}}{4},\\ & {T}_{2}={F}_{i}\cdot \sqrt{1-{\left(\frac{{F}_{i}}{{d}_{2}\cdot /\sqrt{3}}\right)}^{2}}\cdot \frac{{d}_{2}{}^{2}}{4} 。\end{aligned} \right.$ | (4) |
式中:
船用柴油发动机承受冲击作用时,一方面柴油发动机零部件会在冲击载荷下发生形变,另一方面柴油发动机系统会在冲击激励下产生振动。
建立船舶柴油发动机的冲击激励模型:
| $ F\left( t \right) = \sum {} \frac{{{w_i}}}{3}{L_i}\left( {{F_x}{V_x} + {F_y}{V_y} + {M_{xy}}{\theta _i}} \right) 。$ | (5) |
式中:
建立冲击载荷下的能量方程为:
| $ {Q_0} = {\iint\limits_\varOmega {{M_0}{\lambda _1}\left( {\frac{{\partial w}}{{\partial x}} - {\beta _x}} \right)}^2}{\rm{d}}x{\rm{d}}y + {\iint\limits_\Omega {{M_0}{\lambda _2}\left( {\frac{{\partial w}}{{\partial y}} - {\beta _y}} \right)}^2}{\rm{d}}x{\rm{d}}y \text{,} $ | (6) |
式中,
| $ w = \sqrt {\frac{D}{{{\rho _0}L}}} \left[ {{{\left( {\frac{{{M_0}\mu }}{{n{\text{π}} }}} \right)}^2} + {{\left( {\frac{{{E_0}}}{c}} \right)}^{\frac{1}{2}}}} \right] 。$ | (7) |
式中:
计算船舶柴油发动机的固有频率,如下式:
| $ {w_1} ={C_V}\sqrt {\frac{{{j_0}}}{{{\Delta _m}{L_{}}^3}}} \times 0.0167 。$ | (8) |
式中:
船用柴油发动机不同频率的冲击激励幅值如图2所示。可知,冲击激励随着频率呈非线性关系,在频率为3 Hz处达到峰值。

|
图 2 船用柴油发动机不同频率的冲击激励幅值 Fig. 2 Shock excitation amplitudes of different frequencies for marine diesel engines |
针对船用柴油发动机的冲击载荷采集问题,本文采用的传感器为压电振动传感器,该类型传感器基于材料的正压电效应原理,将材料的机械形变转换为电能输出[2]。
压电振动传感器的关键参数包括:
1)机电耦合系数
表征传感器采用的压电材料机械形变与电能的耦合程度,是压电传感器的重要指标,用下式表示:
| $ {K^2} = \frac{{{E_{\rm out}}}}{{{M_{\rm in}}}} \text{。} $ | (9) |
式中:
2)压电应变系数
该系数是指压电材料形变量与电能的转化关系,本文采用冲击能量传感器为正压电传感器,定义为:
| $ d = \frac{D}{T} \text{,} $ | (10) |
式中:
3)相对介电系数
相对介电系数反映的是材料的电介质特性,定义为:
| $ {\varepsilon _r} = \frac{\varepsilon }{{{\varepsilon _o}}} \text{,} $ | (11) |
式中:
建立柴油发动机冲击能量传感器的原理图如图3所示。
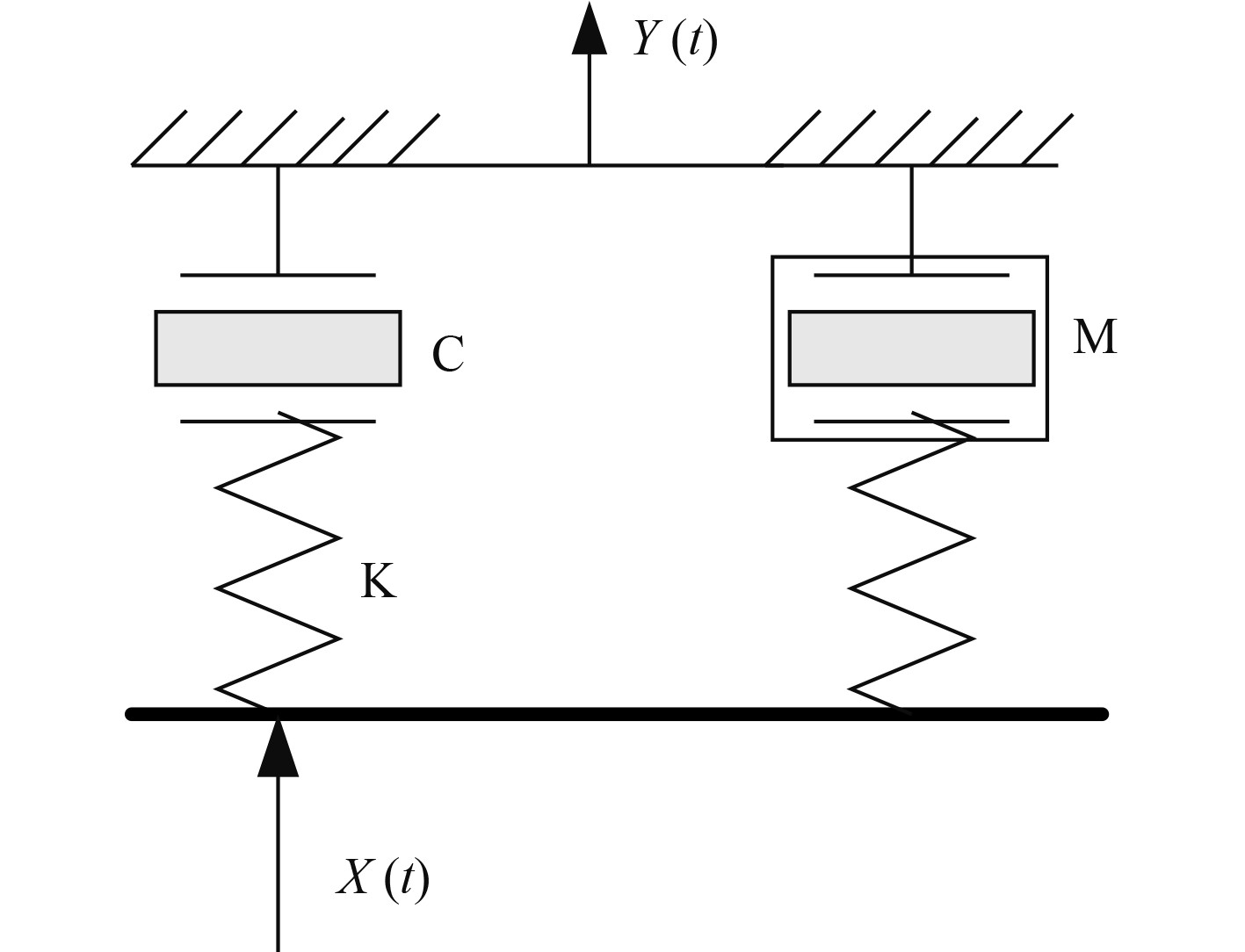
|
图 3 柴油发动机冲击能量传感器的原理图 Fig. 3 Schematic diagram of impulse energy sensor for diesel engine |
当冲击激励为减谐激励
| $ m\ddot y(t) + c\dot y(t) + ky(t) = - m\ddot x(t) 。$ | (12) |
代入减谐激励
| $ y(t) = \frac{{{\omega ^2}}}{{\sqrt {{{\left( {\dfrac{k}{m} - {\omega ^2}} \right)}^2} + {{\left( {\dfrac{{c{\omega _n}}}{m}} \right)}^2}} }}{X_0}\sin \omega t \text{,} $ | (13) |
传感器的无阻尼固有频率
| $ {\omega _n} = \sqrt {\frac{k}{m}}。$ | (14) |
传感器的阻尼比为:
| $ \zeta = \frac{c}{{2m{\omega _n}}} 。$ | (15) |
冲击能量传感器的无阻尼固有频率与阻尼比之间的关系曲线如图4所示。
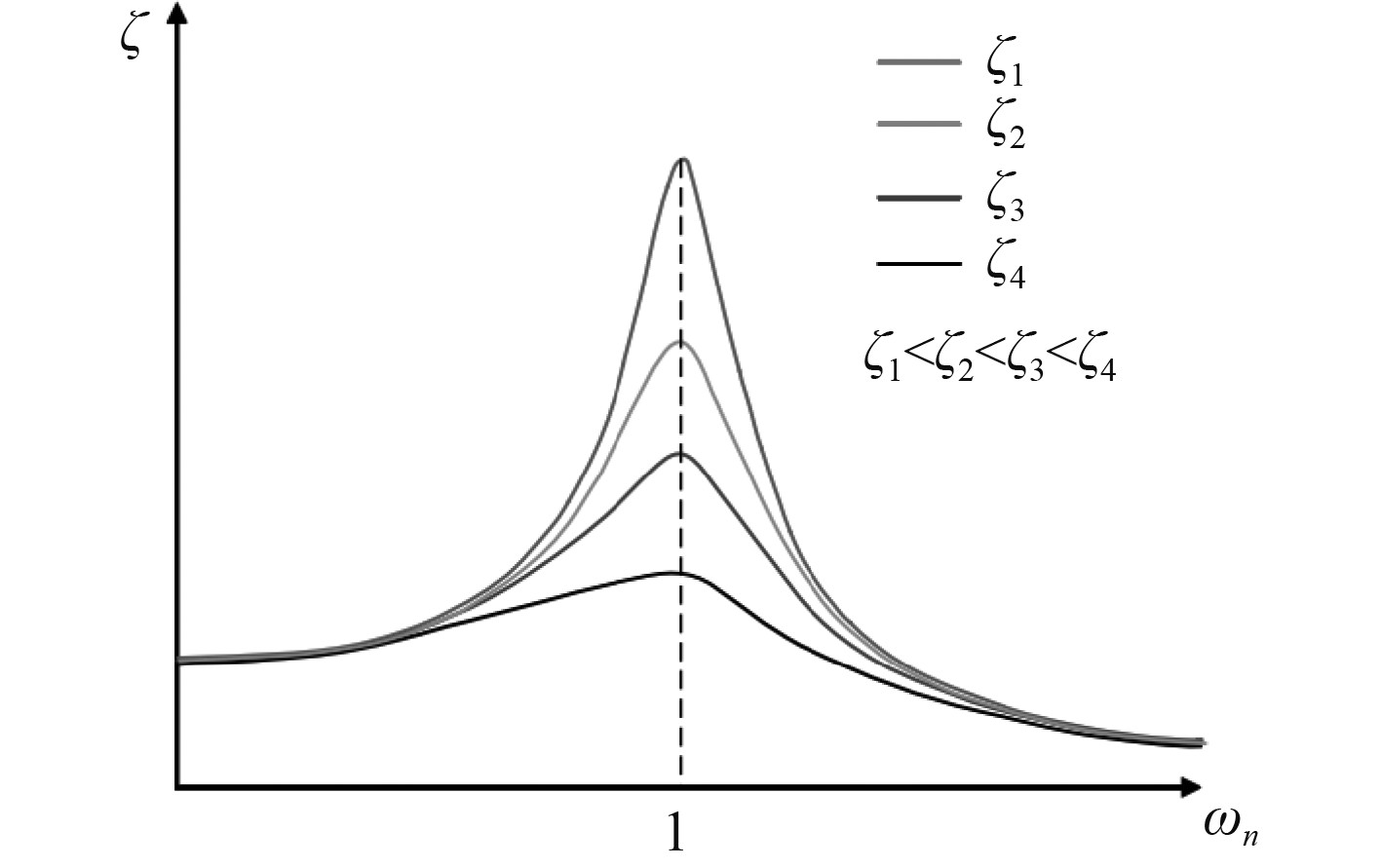
|
图 4 无阻尼固有频率与阻尼比之间的关系曲线 Fig. 4 The relationship between the undamped natural frequency and the damping ratio |
可知,随着固有频率的增加,传感器的阻尼比的峰值(固有频率为1处)逐渐降低。
3.2 船用柴油发动机冲击故障监测系统整体设计本文建立船用柴油发动机冲击故障监测系统,结构如图5所示。
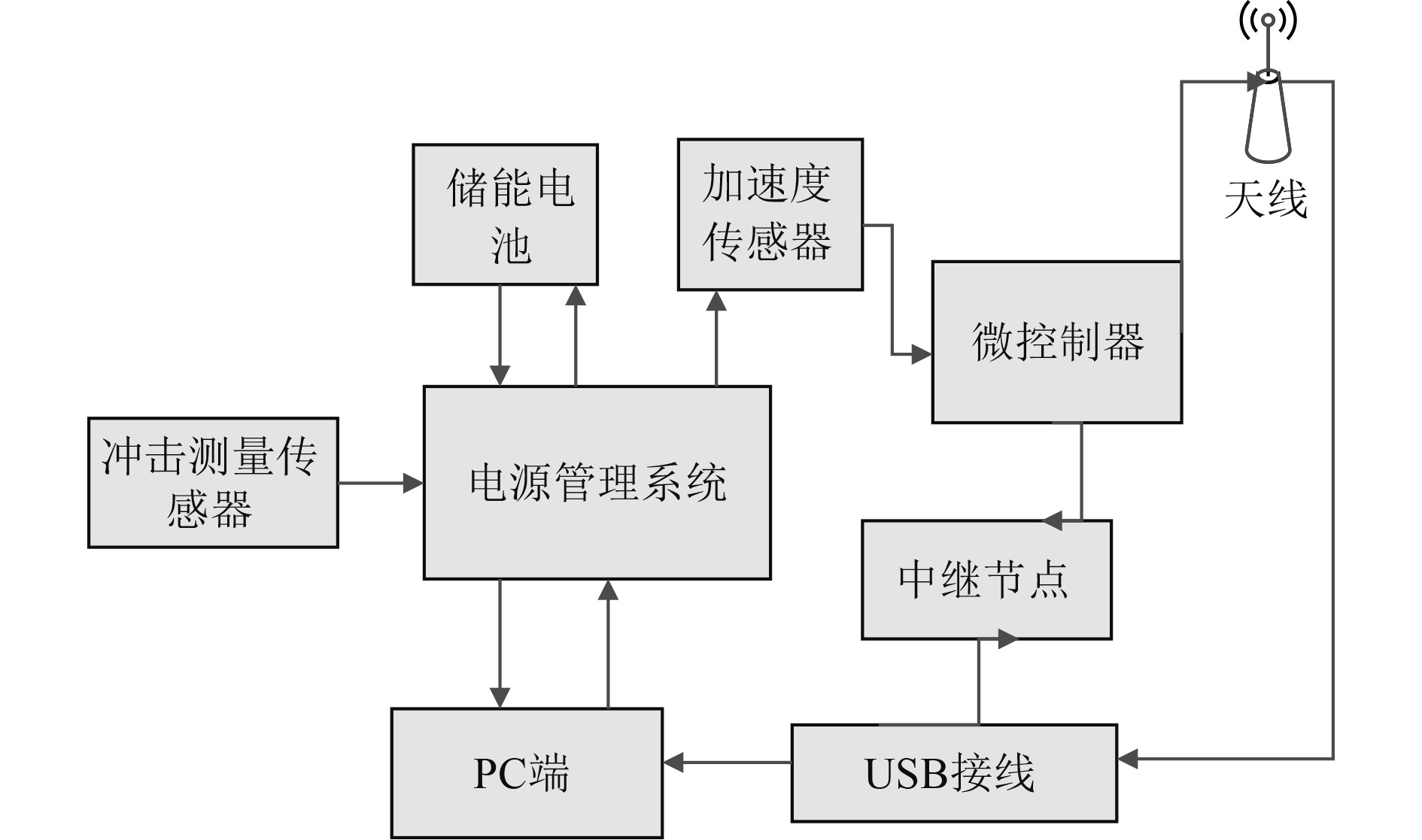
|
图 5 船用柴油发动机冲击故障监测系统结构图 Fig. 5 Structure diagram of impact fault monitoring system for marine chai hair |
1)电源管理系统
为了保障船用柴油发动机故障监测系统的电能供给,通过建立整流、阻抗匹配电路,结合负载对冲击测量传感器进行电能供应,同时利用储能电池将系统多余的电能收集起来。电源管理系统的关键功能包括:① 对传感器的输出交流电压进行整流;② 调节监测系统的电能供给关系,实现电能的最佳配置,采用的电能管理芯片为LTC3588-1芯片。
2)微控制器
微控制器是故障监测和采集的核心,控制器的信号处理频率为600~700 Hz,对振动传感器和能量传感器采集的信号进行分析和处理,当采集的信号超过发动机运行允许的阈值时,微控制器触发报警。
3.3 船用柴油发动机的冲击故障监测系统测试通过搭建冲击测试试验台,对柴油发动机冲击故障监测系统进行仿真测试,测试台主要由以下关键硬件组成:
1)电动式振动台
由小型电机、控制系统和数据采集系统等组成,可以模拟不同的振动模式及频率响应测试。
2)压电式能量传感器
采用PCB压电式能量传感器,采集测试过程的冲击信号。
3)信号发生器
信号发生器的作用是测试和校准测量设备和系统,选用YMC9200型数字信号发生器。
4)示波器
实时显示测试过程的电压、电流、频率等信号的形态、振幅、波形以及相位等特征,选用LA-800示波器[4]。
图6为测试平台采集的船用柴油发动机冲击响应曲线,分别为不同冲击载荷下的幅频值。

|
图 6 测试平台采集的船用柴油发动机冲击响应曲线 Fig. 6 Shock response curve of marine diesel engine collected by test platform |
可知,采样点的个数为400,冲击响应1的谐波幅值在5.5附近波动,冲击响应2的谐波幅值在6.1附近波动。
4 结 语船用柴油发动机在冲击载荷下的工作稳定性非常重要,本文结合柴油发动机的动力学和能量模型,构建船舶柴油发动机冲击故障监测系统,并实际搭建了测试平台,对冲击故障监测系统的功能进行测试。
| [1] |
刘健, 张庆利. 机械传动在冲击载荷作用下的误差检测仿真[J]. 计算机仿真, 2022, 39(7): 437-440+511. LIU Jian, ZHANG Qing-li. Error detection simulation of mechanical transmission under impact load[J]. Computer Simulation, 2022, 39(7): 437-440+511. |
| [2] |
叶伟, 王旭, 陈迎春, 等. 一种特种设备检测用多功能安全帽设计[J]. 设备监理, 2021(4): 34-38+42. YE Wei, WANG Xu, CHEN Ying-chun, et al. Design of multi-functional safety helmet for special equipment testing[J]. Equipment Supervision, 2021(4): 34-38+42. |
| [3] |
郭长虹, 高静, 王阔强, 等. 循环冲击作用下缺陷飞机液压管路微泄漏故障诊断[J]. 液压与气动, 2020(7): 28-35. GUO Chang-hong, GAO Jing, WANG Kuo-qiang, et al. Fault diagnosis of microleakage in hydraulic pipeline of defective aircraft under cyclic impact[J]. Chinese Hydraulics & Pneumatics, 2020(7): 28-35. |
| [4] |
刘欣科, 赵忠辉, 赵锐. 冲击载荷作用下液压支架立柱动态特性研究[J]. 煤炭科学技术, 2012, 40(12): 66-70. LIU Xin-ke, ZHAO Zhong-hui, ZHAO Rui. Under the action of impact load dynamic characteristics of hydraulic support pillar research[J]. Journal of Coal Science and Technology, 2012, 40(12): 66-70. |
 2023, Vol. 45
2023, Vol. 45
