船舶作为主要的交通工具和作战平台,在民用和军用领域发挥着重要作用。随着海上事业的日益发展,对降低船舶的振动噪声提出了更高要求,其中各类旋转机械设备是船舶振动噪声的主要来源之一[1]。滑动轴承具有承载大、可靠性高、耐冲击等优点,是各类旋转机械设备的转子主要支承部件之一[2]。然而,由于缺乏主动控制手段,采用传统滑动轴承支承的旋转机械设备所带来的振动问题突出且难以改变。
目前,减弱旋转机械设备传递到基础的传递力方法主要是在机座与基础之间设置隔振装置。在隔振方面,主要分为被动隔振和主动隔振。被动隔振,如弹簧隔振、橡胶隔振以及气囊隔振等,可有效隔离机械设备的中高频振动向船体传递,但对低频振动的隔离效果不佳。
主动隔振可通过附加力源从而有效抑制低频振动,如压电作动器、液压作动器和电磁作动器等。为获得宽频带隔振效果,目前大多采用主被动隔振相结合的方式,任明可等[3]设计了一种主动压电式作动器和橡胶被动隔振器相结合的复合隔振器,实现了共振频率振幅明显降低。LI等[4]将电磁作动器集成于空气弹簧内部,可承受重载。然而,由于船用动力设备质量较大但船内空间相对狭小,普遍存在着有限安装空间限制隔振器性能的问题。
随着主动磁悬浮轴承技术日益完善,解决旋转机械设备的振动噪声问题有了新的思路。电磁轴承作为一种新型轴承,利用电磁力实现轴承与转子无机械接触[5]。电磁轴承具有无摩擦、高转速、无需润滑和支承特性可控等优点,在航空航天、高速电机、医疗设备[6]以及主动减振降噪等领域有着广泛的应用前景。
目前,电磁轴承在转子振动控制策略中主要分为转子位移最小控制与电磁力最小控制[7]。转子位移最小控制是通过补偿算法增强电磁轴承主动控制作用,从而增加系统动刚度,使转子尽可能围绕定子几何中心转动,提高系统输出精度。在减小传递力方面,主要采取电磁力最小控制。电磁力最小控制是通过滤波算法将反馈位移信号中的不平衡量滤除,降低控制电流不平衡同频分量幅值以降低电磁轴承控制作用,使转子围绕惯性主轴旋转,降低不平衡力从而减小机座到基础的传递力。高辉等[8]应用LMS算法的实时变频切换控制策略,降低周期性不平衡激振力。然而,电磁轴承结构复杂,控制通道和元件数量多,由此带来的可靠性问题不容忽视[9]。
针对滑动轴承振动不可控与电磁轴承可靠性低的问题,本文将滑动轴承高可靠性与高承载力与电磁轴承的支承特性可控等优势相结合,引入电磁-滑动复合轴承(简称复合轴承)这一概念。在复合轴承中,滑动轴承起主要支承作用,电磁轴承作为振动主动控制装置。现有复合支承研究主要集中在抑制转子振动方面上,李慧敏等[10]使转子由滚动轴承于电磁轴承共同支承,经试验验证通过该方法转子振幅下降70%。将电磁轴承与滑动轴承并联,采用H∞ 控制,消除滑动轴承带来的油膜振荡[11]。沈庆崇等[12]在机床主轴增加电磁轴承,进行转子运动轨迹控制,以实现非圆异型截面零件加工。在抑制传递力的研究中,针对轴承力和转子系统共振问题,在滚动轴承基础上并联压电作动器对转子正进动进行补偿,从而消除不平衡力,然而这种支承结构对于大型转子系统难以实现[13]。此外,将推进轴系上的推力轴承与电磁推力轴承并联,通过电磁推力轴承采用PD控制,从而消除轴承座到基础之间的传递力,但该方法只实现轴向单自由度振动抑制且采用反馈控制方法无法很好跟踪轴向传递力变化[14]。
本文以某型三相异步电动机作为研究对象,在滑动轴承基础上并联体积相对较小电磁轴承,针对转子不平衡力所引起的电机机座振动进行主动减振控制。为此,首先建立四自由度电磁-滑动复合轴承-刚性转子系统动力耦合模型。在此基础上,为实时跟踪振动信号获得有效的减振效果,类比主动噪声控制理论[15],应用前馈自适应FxLMS算法[16],以电机机座加速度为0为控制目标进行减振。最后通过仿真验证了该减振方法的有效性。
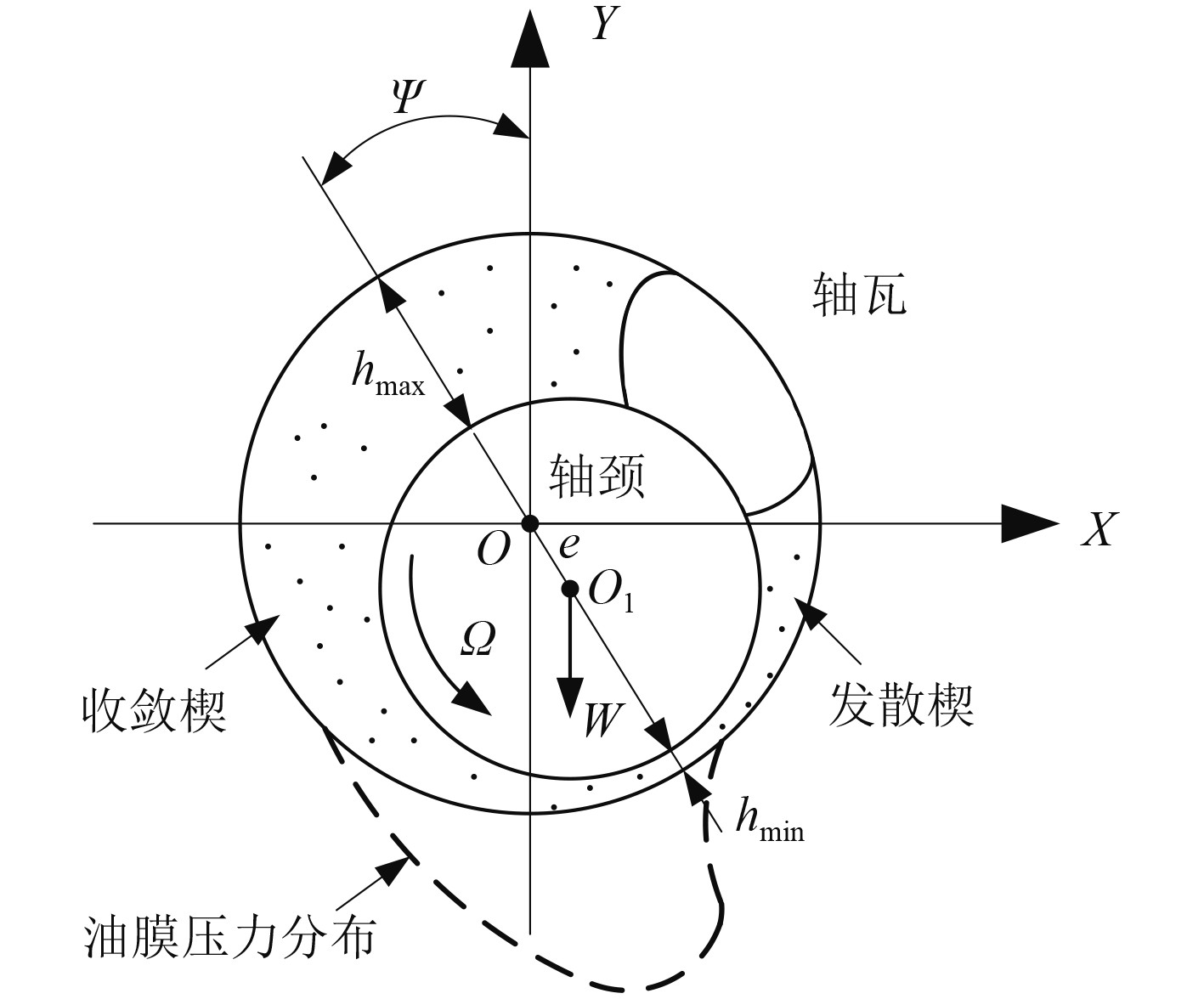
1 模型搭建 1.1 滑动轴承模型以剖分式圆瓦滑动轴承作为转子支承部件。图1为滑动轴承的横截面示意图。滑动轴承由外部轴瓦和内部轴颈组成,两者之间充满粘性的润滑介质,通常为润滑油。工作时,轴颈以一定角速度
|
图 1 滑动轴承工作状态 Fig. 1 Working state of sliding bearing |
此时,轴颈与轴瓦在不同方向上形成不同厚度的油膜间隙,顺着油膜厚度逐渐增大的油楔称为发散楔。此处润滑油压力较小;厚度逐渐减小的油楔形称为收敛楔,此处润滑油受到压缩,产生较大压力,这部分油膜力对轴颈所受负荷起主要支撑作用。
当轴颈在静平衡位置
| $ \left\{ {\begin{gathered} {{F_x} = {F_{x0}} + \frac{{\partial {F_x}}}{{\partial x}}\left| {_0\Delta x + \frac{{\partial {F_x}}}{{\partial y}}\left| {_0\Delta y + } \right.\frac{{\partial {F_x}}}{{\partial \dot x}}\left| {_0\Delta \dot x + } \right.\frac{{\partial {F_x}}}{{\partial \dot y}}\left| {_0\Delta \dot y} \right.} \right.},\\ {{F_y} = {F_{y0}} + \frac{{\partial {F_y}}}{{\partial x}}\left| {_0\Delta x + \frac{{\partial {F_y}}}{{\partial y}}\left| {_0\Delta y + } \right.\frac{{\partial {F_y}}}{{\partial \dot x}}\left| {_0\Delta \dot x + } \right.\frac{{\partial {F_y}}}{{\partial \dot y}}\left| {_0\Delta \dot y} \right.} \right.}。\end{gathered}}\right.$ | (1) |
式中:
定义油膜刚度阻尼系数为:
| $ \begin{gathered} {k_{xx}} = \frac{{\partial {F_x}}}{{\partial x}}\left| {_0} \right.,{k_{xy}} = \frac{{\partial {F_x}}}{{\partial y}}\left| {_0} \right.,{k_{yx}} = \frac{{\partial {F_y}}}{{\partial x}}\left| {_0} \right.,{k_{yy}} = \frac{{\partial {F_y}}}{{\partial y}}\left| {_0} ,\right. \\ {c_{xx}} = \frac{{\partial {F_x}}}{{\partial \dot x}}\left| {_0} \right.,{c_{xy}} = \frac{{\partial {F_x}}}{{\partial \dot y}}\left| {_0} \right.,{c_{yx}} = \frac{{\partial {F_y}}}{{\partial \dot x}}\left| {_0} \right.,{c_{yy}} = \frac{{\partial {F_y}}}{{\partial \dot y}}\left| {_0}。\right. \\ \end{gathered} $ | (2) |
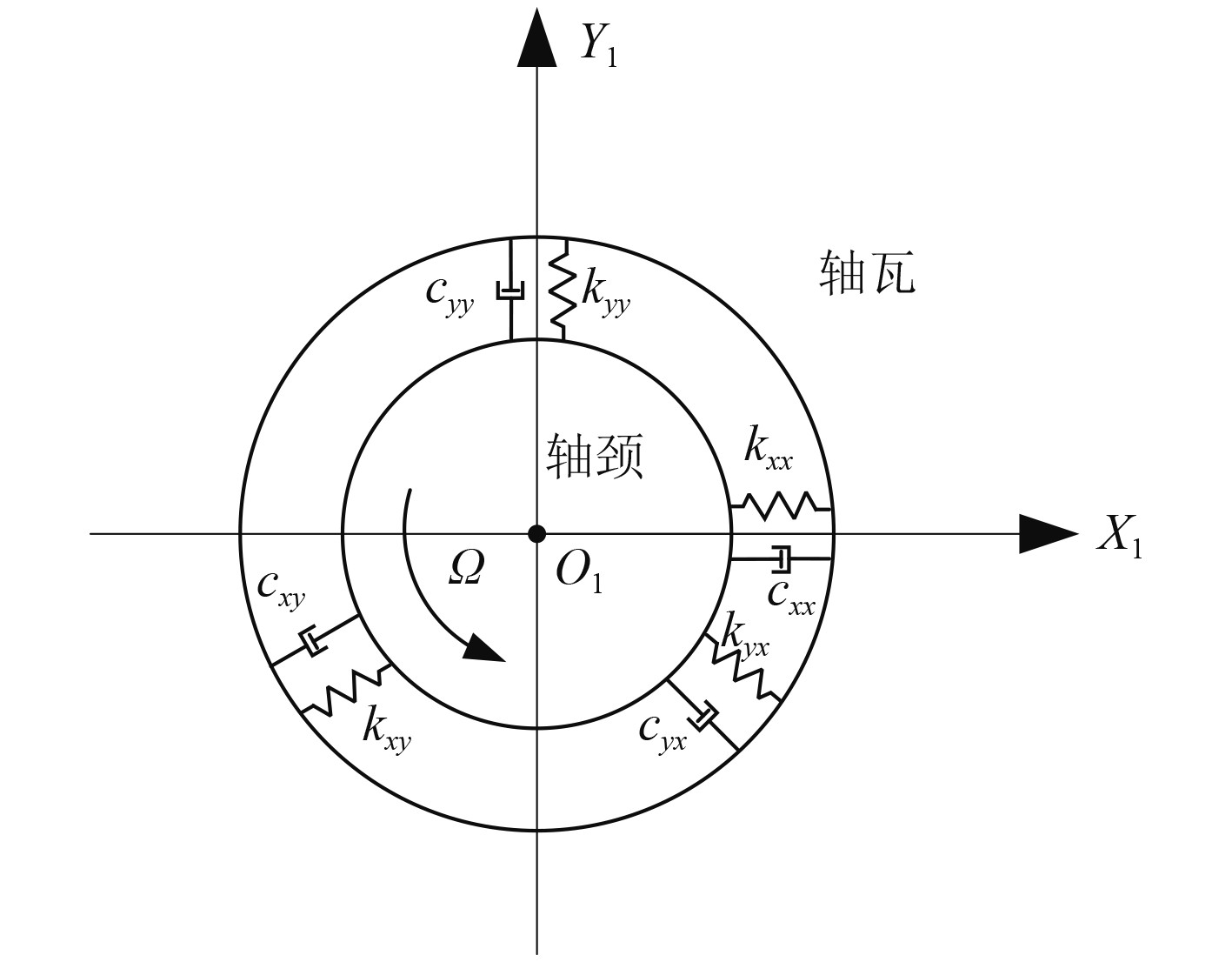
在动态分析中,以静平衡位置
|
图 2 滑动轴承力学模型 Fig. 2 Mechanical model of sliding bearing |
| $ \left[ {\begin{array}{*{20}{c}} {{F_{x1}}} \\ {{F_{y1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{k_{xx}}}&{{k_{xy}}} \\ {{k_{yx}}}&{{k_{yy}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{y_1}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{c_{xx}}}&{{c_{xy}}} \\ {{c_{yx}}}&{{c_{yy}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot x}_1}} \\ {{{\dot y}_1}} \end{array}} \right]。$ | (3) |
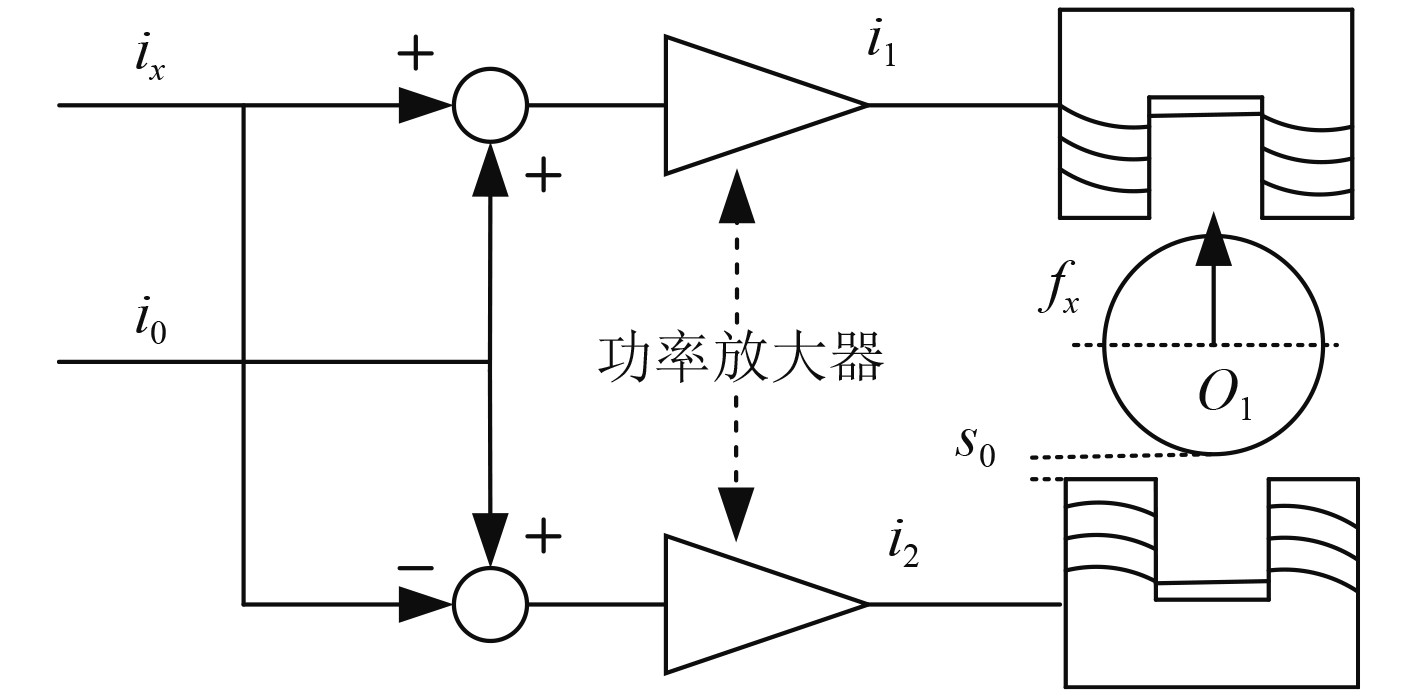
电磁轴承基本原理如图3所示。以
|
图 3 电磁轴承工作原理 Fig. 3 Working principle of active magnetic bearing |
| $ f = \frac{{\partial W}}{{\partial s}} = \frac{{{B^2}A}}{{{\mu _0}}}。$ | (4) |
式中:
忽略铁心磁化作用,磁通密度可表示为:
| $ B = \frac{{ni}}{{2s}} \cdot {\mu _0}。$ | (5) |
式中:
| $ f = \frac{1}{4}{\mu _0}{n^2}A\frac{{{i^2}}}{{{s^2}}} = k\frac{{{i^2}}}{{{s^2}}},k = \frac{1}{4}{\mu _0}{n^2}A 。$ | (6) |
如图3所示,相对的2 组磁极采用差动控制的方式共同作用,由于
| $ \left\{ \begin{gathered} {i_1} = {i_0} + {i_x},\\ {i_2} = {i_0} - {i_x}。\\ \end{gathered} \right. $ | (7) |
式中:
| $ {f_x} = k\left( {\frac{{{{\left( {{i_0} + {i_x}} \right)}^2}}}{{{{\left( {{s_0} - {x_1}} \right)}^2}}} - \frac{{{{\left( {{i_0} - {i_x}} \right)}^2}}}{{{{\left( {{s_0} + {x_1}} \right)}^2}}}} \right)。$ | (8) |
式中:
| $ {f_x} = \frac{{4k{i_0}}}{{s_0^2}}{i_x} + \frac{{4k{i_0}^2}}{{s_0^3}}{x_2} = {k_i}{i_x} - {k_s}{x_2}。$ | (9) |
式中:
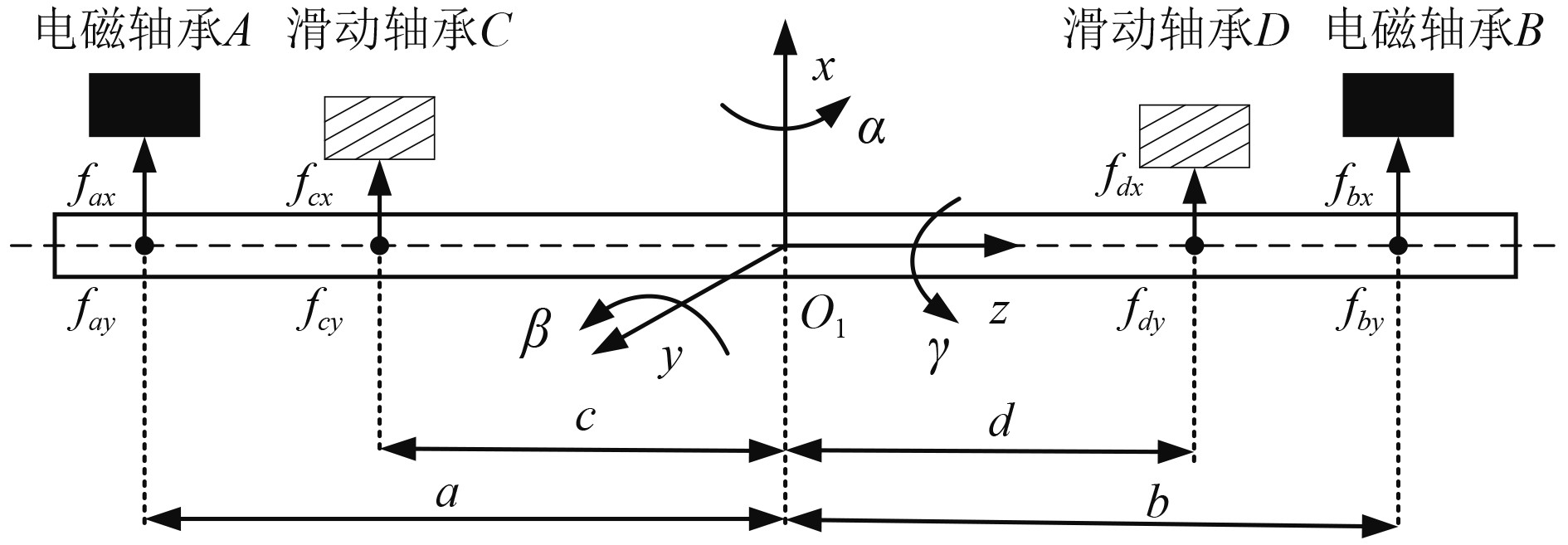
以转子静平衡位置
|
图 4 复合轴承-转子模型 Fig. 4 Composite bearing-rotor model |
将电磁力、油膜力以及不平衡力考虑在内,复合轴承-刚性转子动力学方程:
| $ \begin{gathered} \left[ {\begin{array}{*{20}{c}} {{I_y}}&0&0&0 \\ 0&m&0&0 \\ 0&0&{{I_x}}&0 \\ 0&0&0&m \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\ddot \beta } \\ {\ddot x} \\ { - \ddot \alpha } \\ {\ddot y} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&0&{{I_z}\Omega }&0 \\ 0&0&0&0 \\ { - {I_z}\Omega }&0&0&0 \\ 0&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot \beta } \\ {\dot x} \\ { - \dot \alpha } \\ {\dot y} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} a&b&0&0 \\ 1&1&0&0 \\ 0&0&a&b \\ 0&0&1&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{f_{ax}}} \\ {{f_{bx}}} \\ {{f_{ay}}} \\ {{f_{by}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} c&d&0&0 \\ 1&1&0&0 \\ 0&0&c&d \\ 0&0&1&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{F_{cx1}}} \\ {{F_{dx1}}} \\ {{F_{cy1}}} \\ {{F_{dy1}}} \end{array}} \right] + {F_u}。\\ \end{gathered} $ | (10) |
式中:
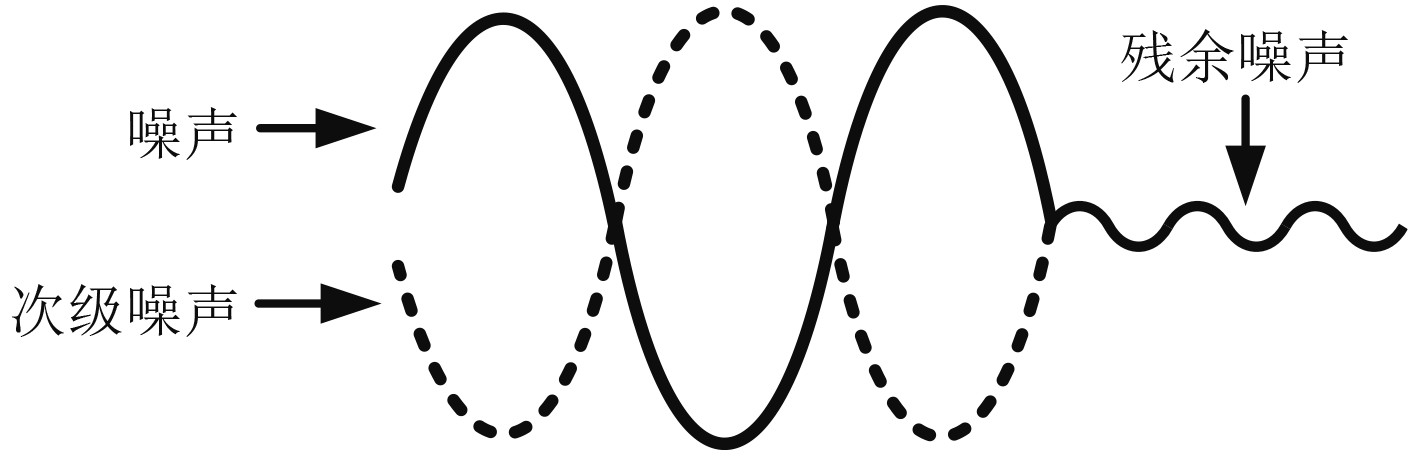
噪声问题的本质是振动问题,振动控制可借鉴噪声控制思路。主动噪声控制(Active Noise Control,ANC)是一种基于声信号叠加原理的噪声消除方法,即产生与噪声源相同振幅相反相位的次级噪声与噪声对消从而达到降噪的目的,其基本原理如图5所示。
|
图 5 噪声对消原理 Fig. 5 Noise cancellation principle |
在主动噪声控制中,反馈型ANC系统无法很好跟踪噪声信号,而前馈型ANC系统通过在目标噪声源处放置参考传感器直接获取参考信号,连同误差传感器测得的误差信号一起作为控制器输入,产生并调节次级噪声与噪声进行对消。

|
图 6 前馈型主动噪声控制 Fig. 6 Feedforward ANC |
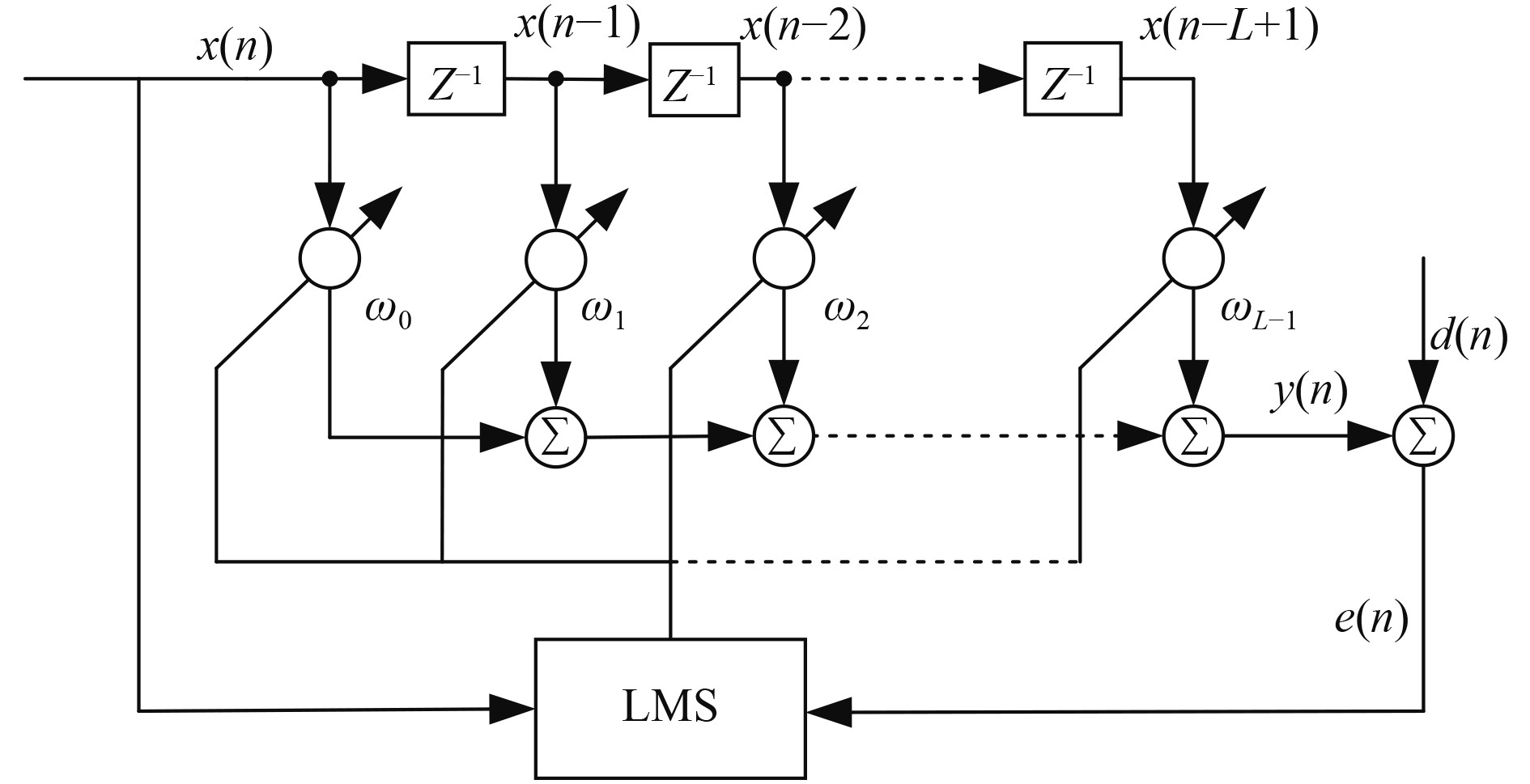
将振动信号类比为噪声信号,振动信号的特性无法预估且具有时变性,导致振动难以被实时跟踪,从而无法有效对消振动。有限脉冲响应(FIR)滤波器可有效跟踪时变信号,通过一定自适应算法,从而产生所需的次级信号。其中最小均方(LMS)算法因其简单易实现而被广泛应用。在n时刻,基于LMS算法的自适滤波器框图如图7所示。
|
图 7 基于LMS算法自适应滤波器 Fig. 7 Adaptive filter based on LMS algorithm |
图7中,
| $ y(n) = {W^{\rm{T}}}(n)X(n),$ | (11) |
| $ e(n) = d(n) - y(n)。$ | (12) |
式中:W(n) = [w0(n), w1(n), ... wL−1(n)]T;X(n) = [x(n)x(n−1), ... x(n−L+1)]T。
根据最速下降法,可以得到N阶FIR滤波器权系数迭代公式,即
| $ W(n + 1) = W(n) + 2\mu e(n)X(n)。$ | (13) |
式中:
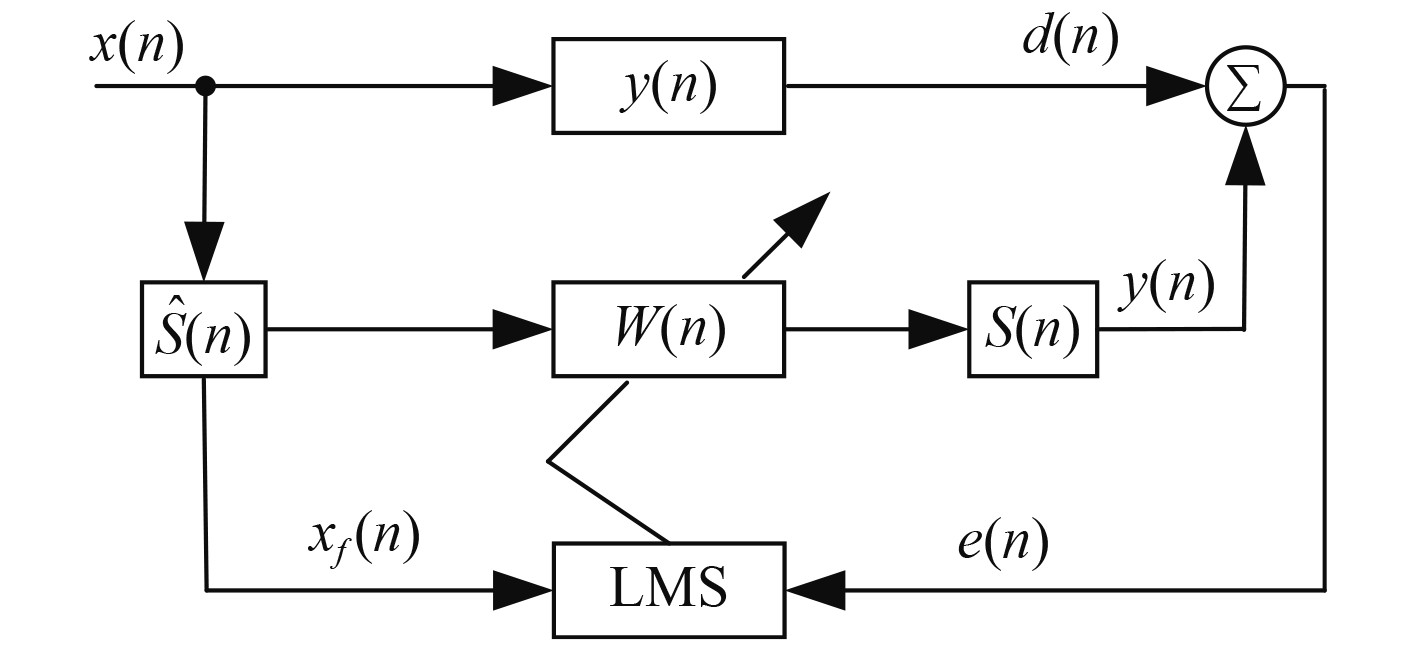
然而,在实际控制中,参考信号
|
图 8 基于FxLMS算法自适应滤波器 Fig. 8 Adaptive filter based on FxLMS algorithm |
使用FxLMS算法后,滤波
| $ {x_f}(n) = \sum\limits_{i = 0}^{L - 1} {{{\hat s}_i}} (n)x(n - i)。$ | (14) |
式中,
滤波器权系数迭代公式为:
| $ W(n + 1) = W(n) - 2\mu e(n){X_f}(n)。$ | (15) |
式中,
在主动减振控制中,以机脚加速度趋近于0作为控制目标进行减振,控制思路如图9所示。依据转速生成参考信号
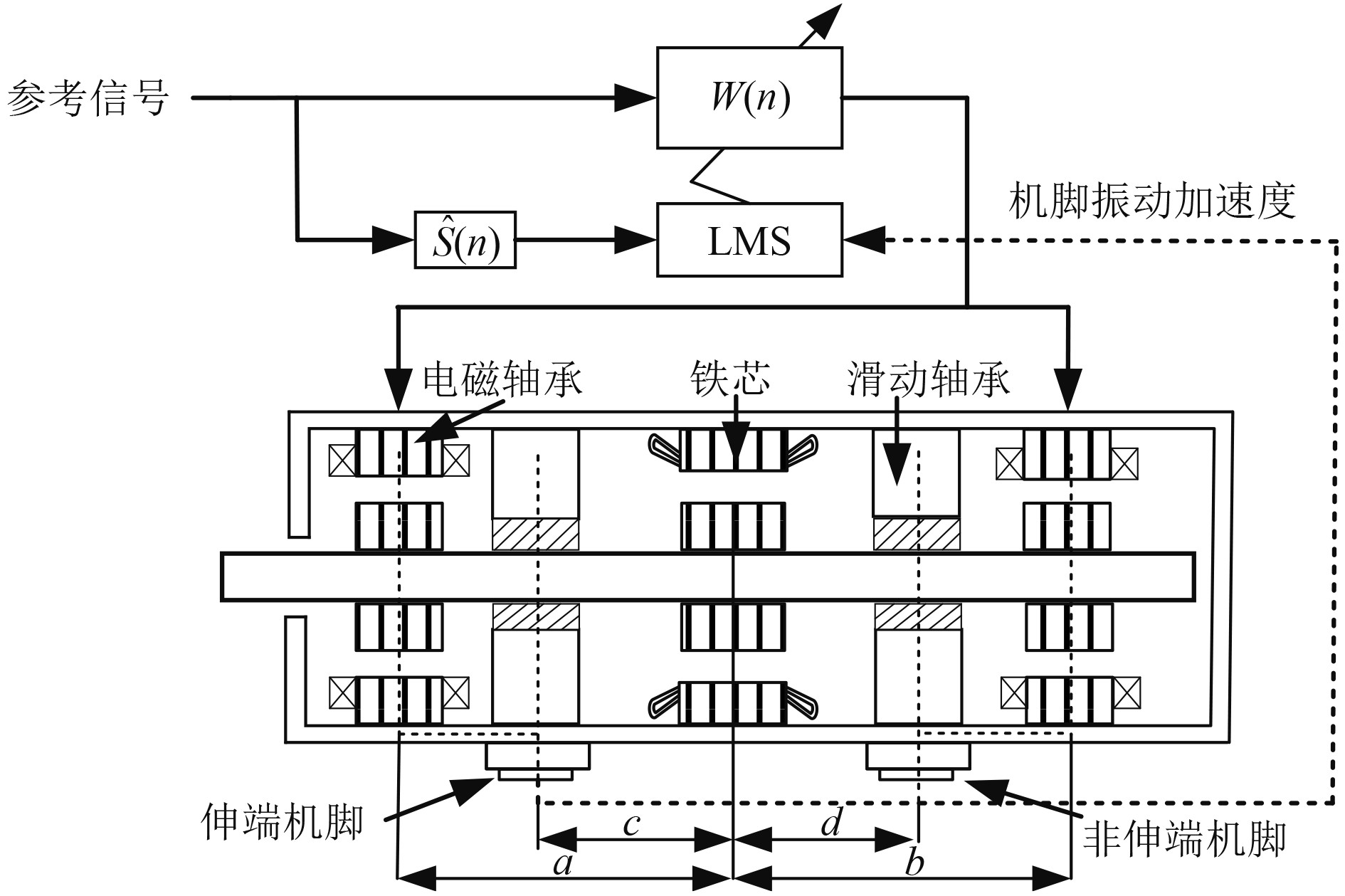
|
图 9 主动减振控制流程图 Fig. 9 Flow chart of active damping control |
通过电磁轴承的控制电流与机脚振动加速度之间的关系可以得到次级通道估计
本文应用Simulink软件,在50 Hz转频下对复合轴承-转子-定子系统仿真,使用Simulink搭建的模型框图如图10所示。仿真具体参数如表1所示。滑动轴承等效刚度阻尼系数如表2所示。
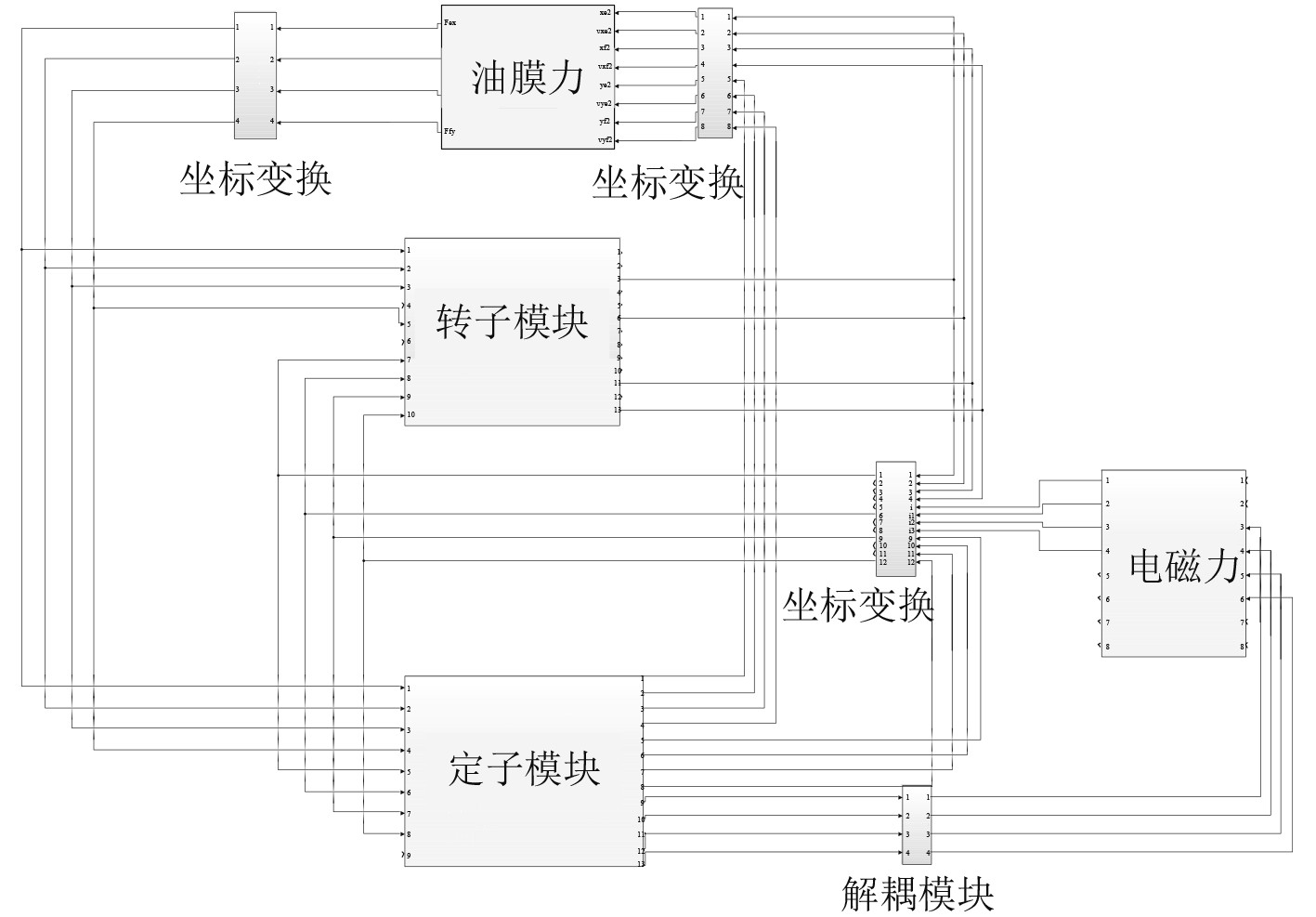
|
图 10 Simulink模型框图 Fig. 10 Simulink model block diagram |
|
|
表 1 模型仿真参数 Tab.1 Model simulation parameters |
|
|
表 2 滑动轴承动力学系数 Tab.2 Dynamic coefficient of sliding bearing |
分别对减振前后2种情况进行仿真,伸端轴承动态传递力变化如图11所示。应用电磁轴承减振后,动态传递力趋于0递减。

|
图 11 减振前后动态传递力对比 Fig. 11 Comparison of dynamic transmission force before and after vibration reduction |
由图12结果可知,电机进行主动减振控制后,机脚振动加速度级分别减小为减振前振动的3.7%和4.2%,结果证明本文所述的控制方法可有效降低电机低频振动。
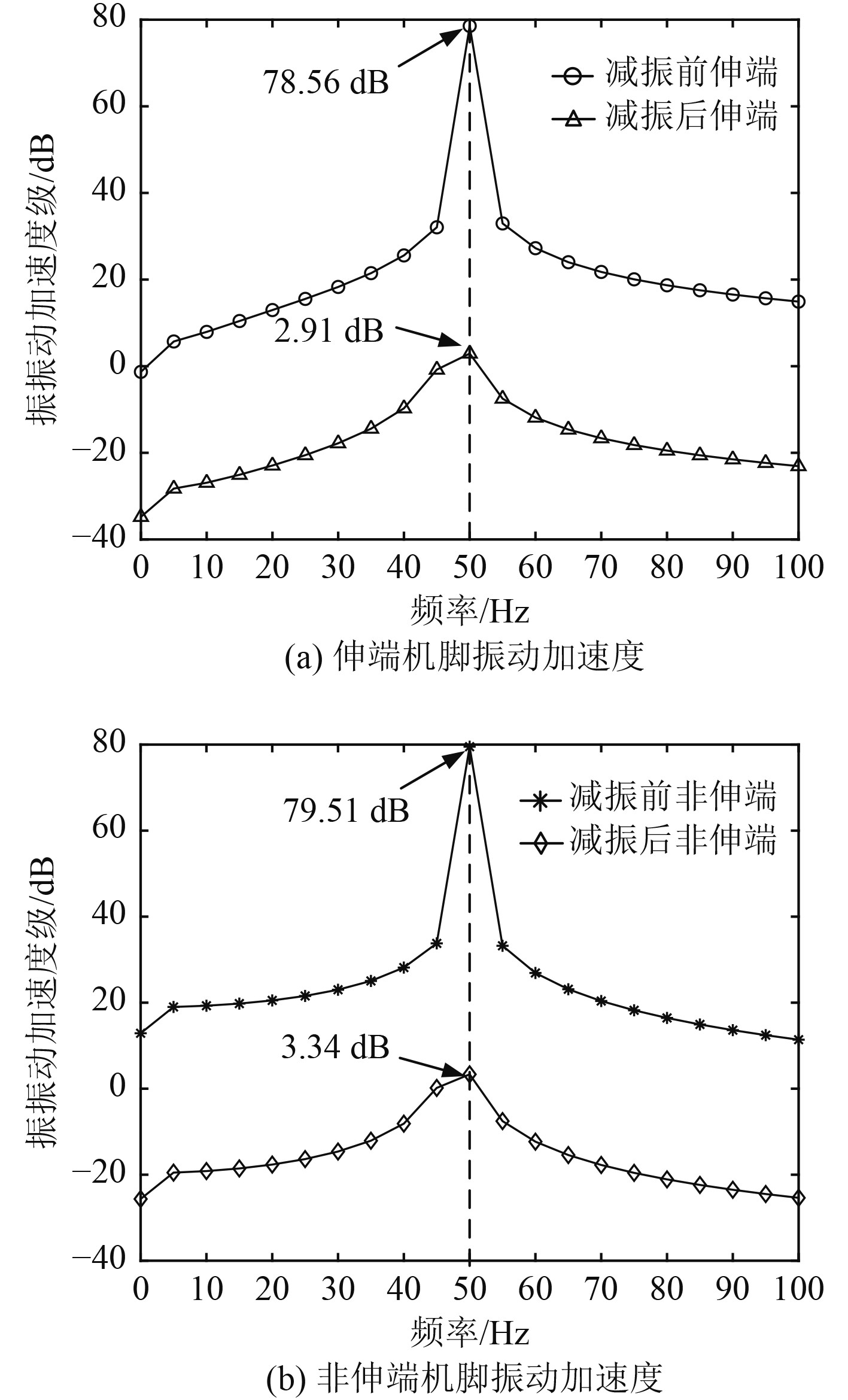
|
图 12 减振前后机脚振动加速度级对比 Fig. 12 Comparison of vibration acceleration levels of machine |
为降低电机在运行状态时的振动,本文提供了一种新的减振思路,即在转子滑动轴承两侧并联电磁轴承,构成电磁-滑动复合轴承从而使得电机振动具备主动控制条件。类比主动噪声控制,应用电磁轴承基于FxLMS算法在机脚处产生一振动加速度,抵消油膜力在机脚处所产生的振动加速度,从而抑制电机低频振动。本文建立四自由度电磁-滑动复合轴承-刚性转子系统动力耦合模型并进行仿真,结果表明该控制方法可有效降低振动至原振动的4%左右。
| [1] |
王东, 姜豪, 苏振中, 等. 船用磁悬浮轴承关键技术与发展综述[J]. 中国电机工程学报, 2020, 40(20): 6704-6715. DOI:10.13334/J.0258-8013.PCSEE.200174 |
| [2] |
钟一谔, 何衍宗, 王正, 等, 转子动力学[M]. 北京: 清华大学出版社, 1987.
|
| [3] |
任明可, 谢溪凌, 黄志伟, 等. 新型橡胶-电磁复合主被动隔振器研究[J]. 振动与冲击, 2021, 40(23): 32-37. REN Mingke, XIE Xiling, HUANG Zhiwei, et al. Research on a new rubber electromagnetic composite active and passive vibration isolator[J]. Vibration and Shock, 2021, 40(23): 32-37. DOI:10.13465/j.cnki.jvs.2021.23.005 |
| [4] |
LI Y, HE L, SHVAI C G, et al. Improved hybrid isolator with maglev actuator integrated in air spring for active-passive isolation of ship machinery vibration[J]. Journal of Sound and Vibration, 2017, 407.
|
| [5] |
GERHARD S, ERICH M. Magnetic bearing: theory, design, and application to rotating machinery [M]. Berlin Heidelberg: Springer-Verlag, 2009.
|
| [6] |
张维煜, 朱熀秋, 袁野. 磁悬浮轴承应用发展及关键技术综述[J]. 电工技术学报, 2015, 30(12): 12-20. DOI:10.3969/j.issn.1000-6753.2015.12.002 |
| [7] |
吴华春, 涂星, 周建, 等. 磁悬浮转子不平衡振动控制研究综述[J]. 轴承, 2022(3): 1-9. |
| [8] |
高辉, 徐龙祥. 基于LMS算法的磁悬浮轴承系统振动补偿[J]. 振动工程学报, 2009, 22(6): 583-588. DOI:10.3969/j.issn.1004-4523.2009.06.005 |
| [9] |
李田. 磁悬浮轴承的容错控制系统研究[D]. 武汉: 华中科技大学, 2019.
|
| [10] |
李慧敏, 曾胜, 汪希萱. 电磁辅助支承的被动式减振研究[J]. 中国机械工程, 2003(24): 24-26+4-5. DOI:10.3321/j.issn:1004-132X.2003.24.006 |
| [11] |
DIMITRI A S, El SHAFEI A , ADLY A A, MAHFOUD J . Magnetic actuator control of oil whip instability in bearings[J]. IEEE Transactions on Magnetics, 2015, 51(11).
|
| [12] |
沈庆崇, 马金奎, 常记莽, 等. 滑动轴承转子运动轨迹主动控制[J]. 润滑与密封, 2010, 35(12): 69–73+82.
|
| [13] |
S HEINDEL, F BECKER, S RINDERKNECHT . Unbalance and resonance elimination with active bearings on a Jeffcott Rotor[J]. Mechanical System and Signal Processing, 2016, 85: 339–353.
|
| [14] |
LEWIS D W, ALLAIRE P E, THOMAS P W. Active magnetic control of oscillatory axial shaft vibrations in ship shaft transmission systems part 1: system natural frequencies and laboratory scale model[J]. A S L E Transactions, 1989, 32(2): 170-178. |
| [15] |
HAO Z A , DLWA B. Deep ANC: A deep learning approach to active noise control[J]. Neural Networks, 2021, 141: 1–10.
|
| [16] |
刘昊, 杨智春, 牛文超, 等. 基于NAF-FxLMS控制器的垂尾抖振主动控制[J]. 振动与冲击, 2021, 40(6): 140-146. LIU Hao, YANG Zhichun, NIU Wenchao, et al. Active control of vertical tail buffeting based on NaF FXLMS controller[J]. Vibration and Shock, 2021, 40(6): 140-146. DOI:10.13465/j.cnki.jvs.2021.06.019 |
 2023, Vol. 45
2023, Vol. 45
