2. 郑州航空工业管理学院,河南 郑州 450000
2. Zhengzhou University of Aeronautics, Zhengzhou 450000, China
为了加强国防建设,知己知彼,分析对方的海军装备并对己方相关设备进行改进,显得尤为急迫且重要[1-3]。美军近年来在海军新装备上取得了突破性进展,其中的“忠诚僚机”是由美国空军研究实验室在2015年提出的实验项目,可以提供高效、灵活的编队自主控制系统,尽早实现多型号协同编队飞行,旨在确保其可以在复杂对抗环境中占有先机。本文从材料学、声学以及流体力学等跨领域角度入手展开分析,对舰载无人机的外形更新升级带来一定的参考价值[4-6]。
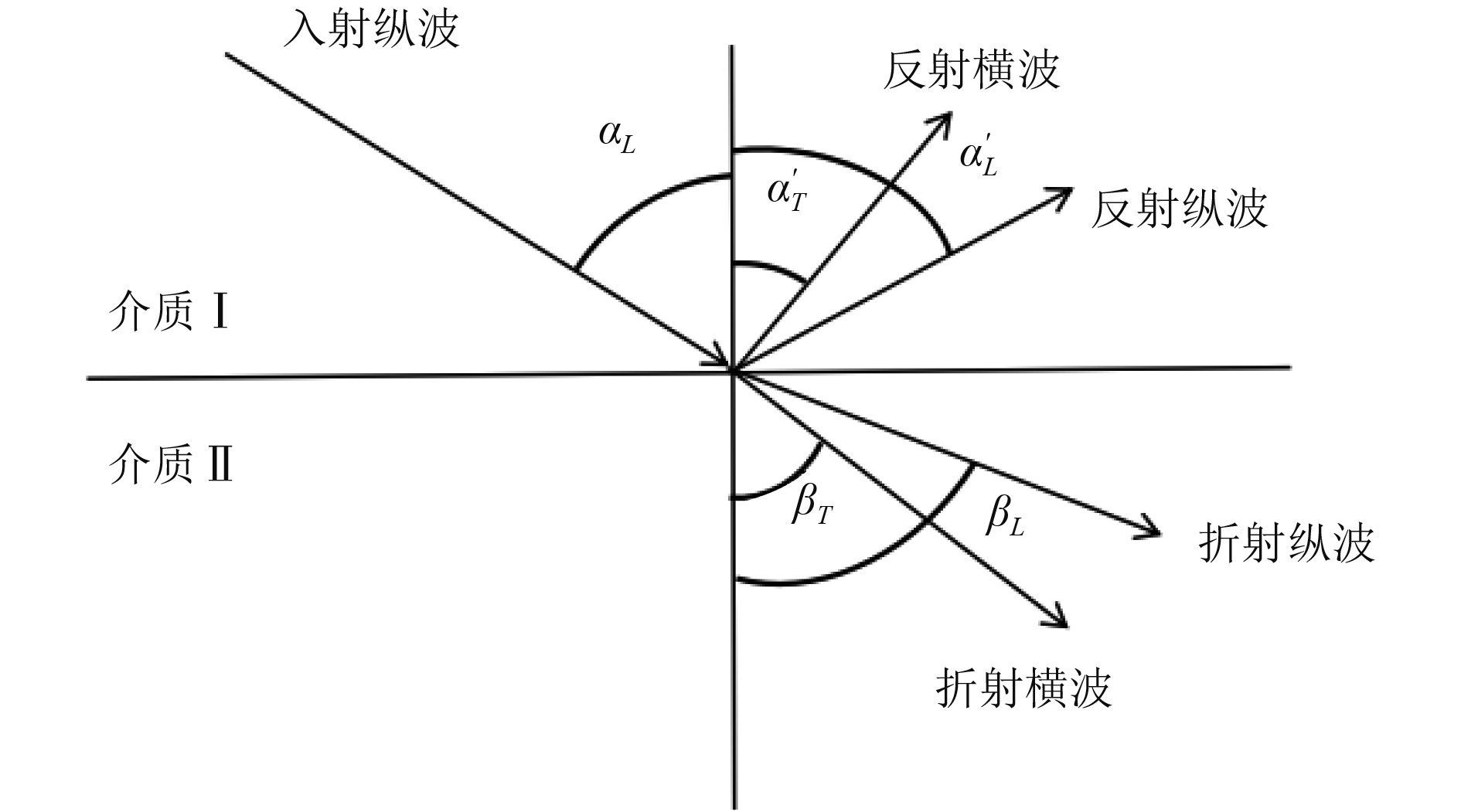
1 基于参数化设计临界折射纵波分析如图1所示,超声波一般具有速射、传播、反射、波形转换等特性,所以当超声波从一种介质以一定角度倾斜射入另一介质中时,会发生超声波的反射、折射现象,甚至波形也可能会产生变化。
|
图 1 超声纵波入射、反射以及折射图 Fig. 1 Ultrasonic longitudinal wave incidence, reflection, and refraction diagram |
其中入射纵波与法线之间的夹角为入射角,记为αL。这些反射角、折射角以及入射角与声波的波速之间满足snell定律:
| $ \frac{{\sin {\alpha _L}}}{{{C_{L1}}}} = \frac{{\sin \alpha _L^{'}}}{{{C_{L1}}}} = \frac{{\sin \alpha _T^{'}}}{{{C_{T1}}}} = \frac{{\sin {\beta _L}}}{{{C_{L2}}}} = \frac{{\sin {\beta _T}}}{{{C_{T2}}}}。$ |
式中:CL1和CT1分别为介质Ⅰ中纵波的波速和横波的波速,CL2和CT2分别为介质Ⅱ中纵波的波速和横波的波速。
当入射纵波以某一角度从介质Ⅰ射入介质Ⅱ中使得折射角βL等于90°,则称此时的入射角为第一临界角,此时的折射纵波会沿着介质在一定深度内进行传播,称该纵波为临界折射纵波,第一临界角可通过2个介质中的纵波波速求得:
| $ {\alpha _L} = {\sin ^{ - 1}}\left(\frac{{C{}_{L1}}}{{C{}_{L2}}}\right)。$ |
本次设计是以Matlab为基础改变材料的参数研究舰载无人机的特性,按照5个步骤展开。
步骤1 根据Mason等效电路推导出来的解析式:
| $ {K_{{s}}} = - \frac{{{{{n}}^2}}}{{{C_0}}} 。$ |
式中:Ks为弹簧软化系数,n为机电转换比,C0为单位电容。
步骤2 根据Spring-mass模型推导出解析式:
| $ {Z_{{m}}} = - {{j}} \times 2L\frac{{8L3\left( {T + P} \right) + 12{{{a}}^2}T\left( {1 - {\sigma ^2}} \right)}}{{3{{{a}}^4}\left( {1 - {\sigma ^2}} \right)\varpi }} + j\varpi 2\rho L 。$ |
可以得出:
| $ {C_Z} = - \frac{{3{{a}^4}\left( {1 - {\sigma ^2}} \right)}}{{16{L^3}\left( {T + P} \right) + 12{{a}^2}T\left( {1 - {\sigma ^2}} \right)}} \text{,} $ |
| $ {L_Z} = 2\rho L。$ |
式中:
步骤3 计算吸合电压:
| $ {V_{{{pi}}}} = \sqrt {\frac{{8{{g}}_{\text{0}}^{\text{3}}{{k}}}}{{27A{{{\varepsilon }}_{\text{0}}}}}} \text{。} $ |
式中:Vpi为吸合电压,A为电容的等效面积,
步骤4 得出谐振频率:
| $ {\omega _0} = \frac{{2.95L}}{{{{{a}}^2}}}\sqrt {\frac{E}{{{\rho _P}\left( {1 - {\sigma ^2}} \right)}}} = \sqrt {\frac{{{{{k}}_{eq}}}}{{{{{m}}_{eq}}}}} \text{。} $ |
式中:w0为谐振频率,L为薄膜厚度,
步骤5 基于以上公式结果,使用Matlab软件,改变低应力氮化硅薄膜的舰载无人机的参数包括薄膜半径、厚度、空腔厚度、绝缘层厚度等,研究比较对CMUT的工作频率、吸合电压的影响。对同一参数的不同数值得到的结果进行比较,可以使舰载无人机达到性能最优化。
2.2 参数计算在本次关于舰载无人机的外形设计上,为了可以提升其飞行性能,特采取了超声成像系统对其相关数据加以搜集,旨在提升其指向性。因此在关于舰载无人机阵列间距和声波的波长上,得出如下公式:
| $ {{d}} \leqslant \frac{\lambda }{{1 + {\text{sin}}\left( {{\theta _{\text{s}}}} \right)}} \text{。} $ |
与此同时,为了更好地消除噪声对于舰载无人机的影响,对其进行优化,得出最大偏转角度:
| $ {{dex}} \leqslant \frac{\lambda }{{1 + {\text{sin}}\left( {{\theta _{\text{s}}}} \right)}} \times \frac{{N - 1}}{N} \text{,} $ |
| $ {\left( {{\theta _{\text{s}}}} \right)_{{\text{max}}}} = {\text{arcsin}}\left( {\frac{\lambda }{{{d}}} \times \frac{{N - 1}}{N} - 1} \right) \text{。} $ |
由此可见,适时增加阵元数目,除了可以减小主瓣宽度外,还可以抑制旁瓣能量对舰载无人机的影响。最终,假设距离为y=l0、20、30、40 cm时,进行信号的发射和接收,对其发射性能进行测试,设偏置电压为Vdc=20 V,交流电压频率为f=[100 kHz, 1000 kHz],信号重复个数为5个。CMUT与标准舰载无人机之间的距离L=20 cm,对其信号质量进行测试,得出如表1所示的相关参数。
|
|
表 1 激励信号重复数与接收信号幅值 Tab.1 Repetitions of excitation signals and amplitudes of received signals |
借助风速预测,对舰载无人机外形进行测试,本文选取的是支持向量机(SVM)结合K-means聚类算法的混合模型。其中支持向量机是由非线性公式y(x)=f(xi)+ei给出,估计模型如下式:
| $ y(x) = {w_t}\phi ({x_i}) + b + {e_i} \text{。} $ |
为了缩小误差,对重量向量函数w和偏差项b进行优化,得到:
| $ {\text{min}}_{{w}\text{,}{b}\text{,}{e}}J({w}\text{,}{e})=1/2{w}_{t}w+v1/2{\displaystyle \sum _{i=1}^{N}{e}^{2}i} \text{,} $ |
其等式约束为:
| $ {{{y}}_{{i}}} = {{{w}}_{{t}}}\psi \left( {{{{x}}_{{i}}}} \right) + {{b}} + {{{e}}_{{i}}} {,} $ |
在满足上式条件后,将拉格朗日乘数赋予,得到:
| $ L\left( {w,b,e,a} \right) = J\left( {w,e} \right) - \sum\limits_{i = 1}^N {{\alpha _i}\left( {{w_t}\phi \left( {{x_i}} \right) + b + {e_i} - {y_i}} \right)} \text{。} $ |
经公式变换,消去w和ei,进行线性化得到:
| $ \left[ {\begin{array}{*{20}{c}} 0 \\ y \end{array}\begin{array}{*{20}{c}} {} \\ {} \end{array}\begin{array}{*{20}{c}} {yT} \\ {\varpi + 1/\gamma } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} b \\ a \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ {{1_\vartheta }} \end{array}} \right] \text{。} $ |
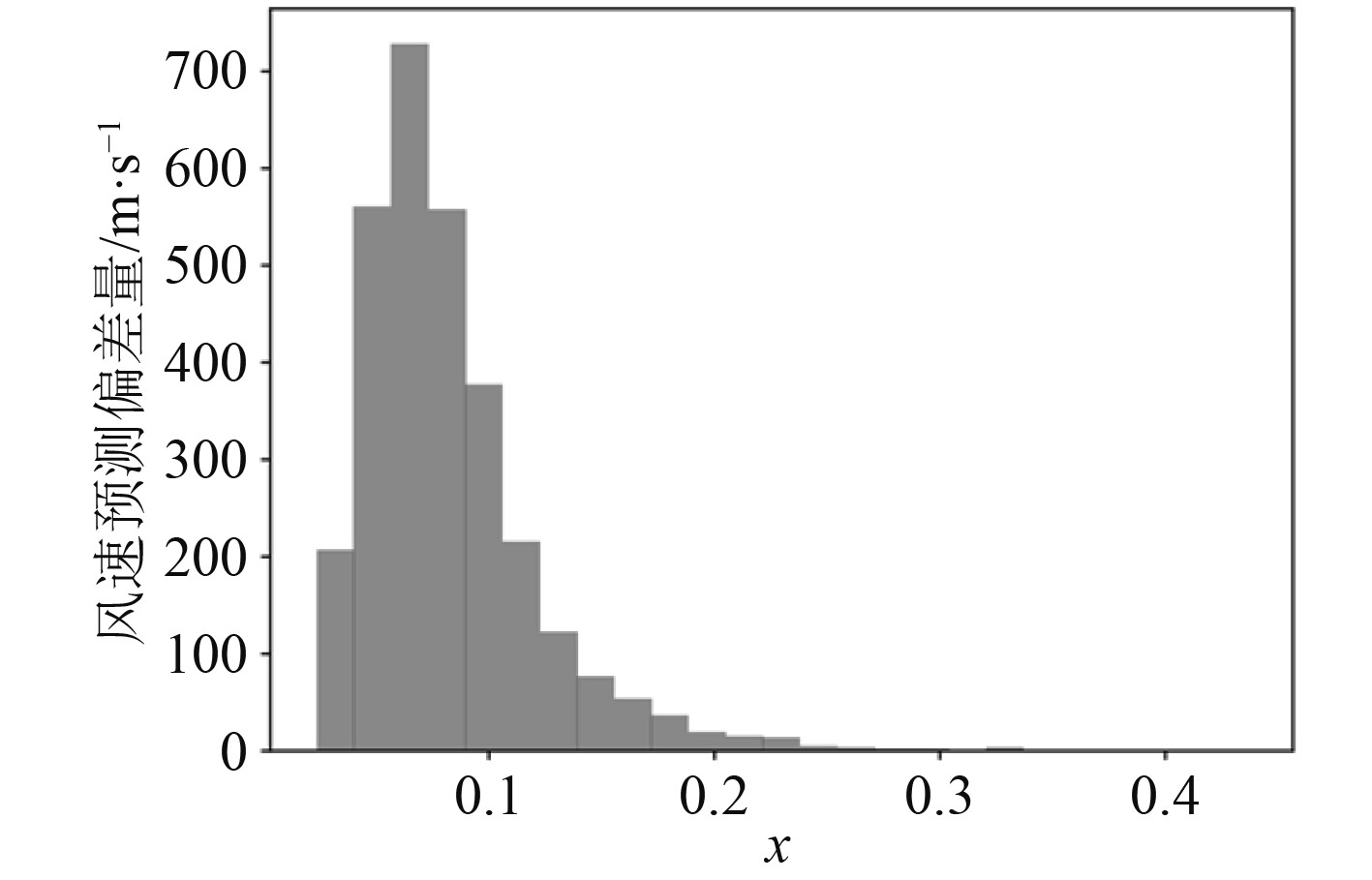
基于以上结果,建立预测模型,并对整个训练数据进行刻画。为了让本次研究的参数更具参考性,将搜集的结果进行平均值处理。风速预测偏差量与X参数的相关性如图2所示。
|
图 2 风速预测偏差量与X参数的相关性 Fig. 2 Correlation between wind speed forecast deviation and Xparameters |
按照相关计算公式,对现有舰载无人机的相关数据进行搜集比对,并在现有较成熟的姿态解算算法中,围绕舰载无人机的角速度和加速度进行姿态算法分析,并对其磁力计加以矫正,以起到随时纠正的目的。
在本次研究中采用成本低廉的mems传感器。由于其噪声大,容易暴露,因此在材料上对其加以改进,对外界的磁场、重力、时间等参数进行充分考量,并将这些数据与材料学加以融合,由此提升舰载无人机的飞控姿态。
3.2 欧拉角和四元数分析欧拉角公式广泛应用于多个独立角参数的处理。在航姿中把它们称作俯仰角、翻腾角和偏航角。人体坐标系与地理坐标系之间的夹角是飞机的姿态角,也称为欧拉角。
四元数在航姿中的意义为一个向量(x,y,z)绕角度θ旋转。故而,在关于方向余弦矩阵中,也将沿用前文思路,继续采取表示物体的姿态,得出载体坐标系转换到地理坐标系:
| $ \left| {\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}}&{{C_{13}}} \\ {{C_{21}}}&{{C_{22}}}&{{C_{23}}} \\ {{C_{31}}}&{{C_{32}}}&{{C_{33}}} \end{array}} \right|T*\left| {\begin{array}{*{20}{c}} a \\ b \\ c \end{array}} \right| \text{。} $ |
其中,向量(a,b,c)可以为3轴加速度数据。
3.3 Mahony互补滤波向量积的定义:
| $ {\text{a}} \times {\text{b}} = \left| {\text{a}} \right|\left| {\text{b}} \right|\cdot {\text{sin}}\theta \text{。} $ |
在这里θ为两向量之间的夹角(共起点的前提下)(0°≤θ≤180°)
将a向量与b向量做叉积,得到e向量(误差向量):
| $ ex = (ay \cdot vz - az\cdot vy)\text{,} $ |
| $ ey = (az \cdot vx - ax \cdot vz)\text{,} $ |
| $ ez = (ax \cdot vy - ay \cdot vx)\text{。} $ |
通过四元数微分方程(角速度与四元数的关系),将补偿修正过的角速度数据(g向量)转换成四元数,并将四元数归一化。
4 舰载无人机外形的数学模型构建经前文分析可知,舰载无人机的运动模拟中,声波、风速都会导致舰载无人机相对距离、径向速度、角度等信息的变化以及多普勒频率的变化。故而在平移变换参数上,选取其平移变换矩阵方程为:
| $ \left( {\begin{array}{*{20}{c}} {{X_n}} \\ {{Y_n}} \\ {{Z_n}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{X_0}} \\ {{Y_0}} \\ {{Z_0}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{X_{0n}}} \\ {{Y_{0n}}} \\ {{Z_{0n}}} \end{array}} \right) \text{。} $ |
在旋转变换上,舰载无人机的中心保持在Z轴不动,OXY旋转,其旋转矩阵:
| $ {T_2}\left( \alpha \right) = \left( {\begin{array}{*{20}{c}} {{\text{cos}}\alpha }&{{\text{sin}}\alpha }&0 \\ { - {\text{sin}}\alpha }&{{\text{cos}}\alpha }&0 \\ 0&0&1 \end{array}} \right) \text{。} $ |
保持X轴不动,OYZ轴按照逆时针旋转,旋转的矩阵:
| $ {T_x}\left( \beta \right) = \left( {\begin{array}{*{20}{c}} 1&{\text{0}}&0 \\ 0&{{\text{cos}}\beta }&{\sin \beta } \\ 0&{{{ - }}\sin \beta }&{{\text{cos}}\beta } \end{array}} \right) \text{。} $ |
保持Y轴不动,OXZ轴按照逆时针旋转,旋转的矩阵:
| $ {T_y}\left( \gamma \right) = \left( {\begin{array}{*{20}{c}} {{\text{cos}}\gamma }&{\text{0}}&{{{ - }}\sin \gamma } \\ 0&1&0 \\ {\sin \gamma }&0&{{\text{cos}}\gamma } \end{array}} \right) \text{。} $ |
最终基于以上参数,计算出不同坐标系之间的旋转变换。
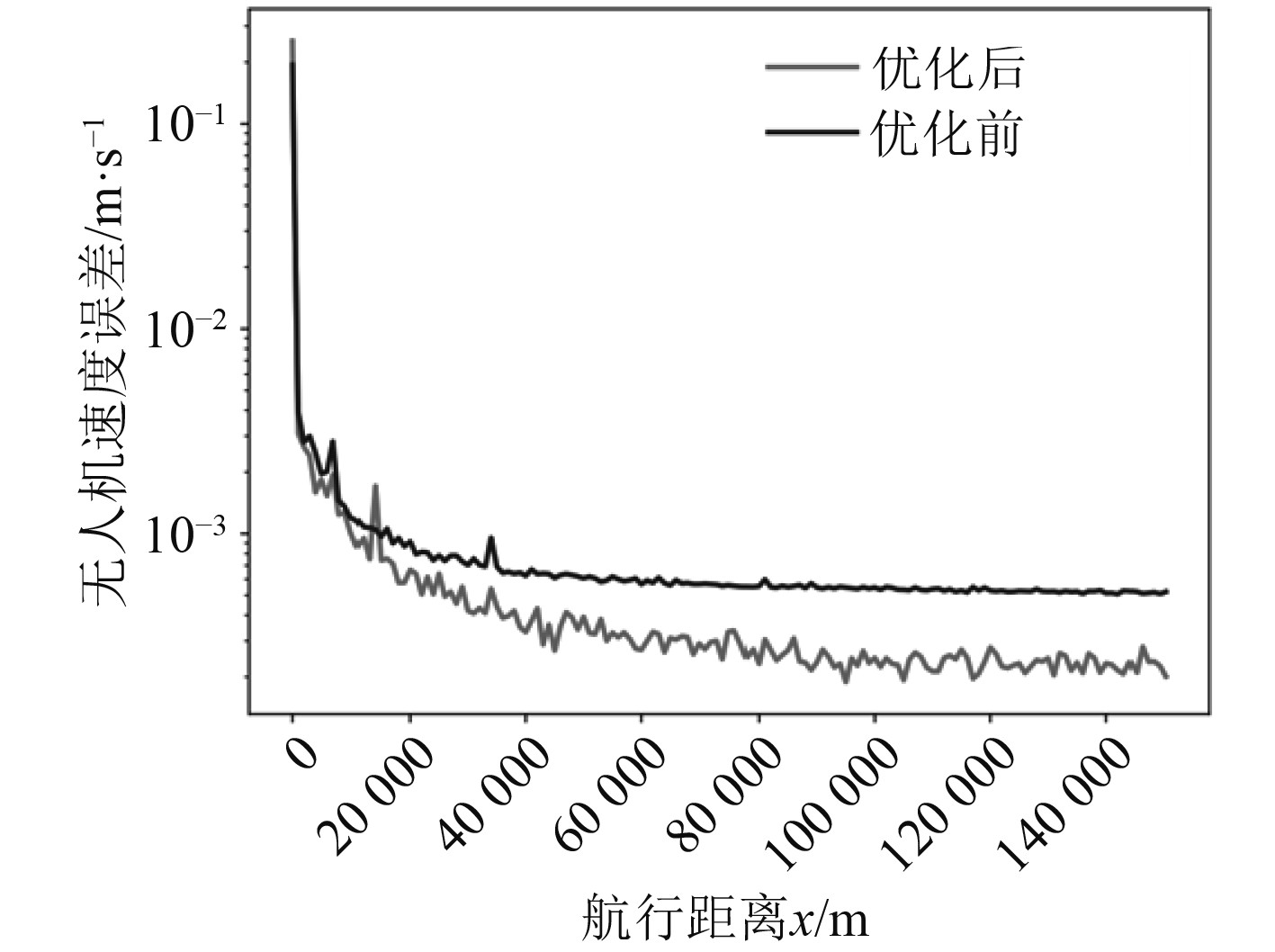
基于以上计算,可以得到翼展4 m,机身长2.8 m,整个机身空重只有4.5 kg的无人机模型。无人机速度误差曲线与航行距离之间的关系曲线如图3所示。整体趋向于流线型,降低了风的阻力,也降低了造价,总体机身以塑料、复合材料为主要材料,也有小部分为金属巩固。
|
图 3 无人机速度误差曲线与航行距离之间的关系曲线 Fig. 3 The relationship curve between the UAV speed error curve and the sailing distance |
为了提升舰载无人机的作战效能,增强其隐蔽性、生存性以及战术性,进而在理论上提升其攻击性及侦察功能。本文重点分析了舰载无人机的数学模型,着重对其气动外形的设计进行优化,从而可以获得更好的无人机外形,进一步提高其各方面的作战性能。
| [1] |
安金坤, 方峰, 曾巍. 一种基于双测度的参数重叠舰载雷达型号自动识别方法[J]. 电子信息对抗技术, 2022, 37(3): 16-19+25. |
| [2] |
崔恒荣, 秦雅, 卞玮章. 基于模糊控制参数自整定的舰载雷达三轴稳定控制[J]. 雷达与对抗, 2020, 40(1): 57-60. |
| [3] |
邓恩民, 刘冬利, 侯建强, 等. 基于参数反演的舰载雷达探测威力预报方法[J]. 空军预警学院学报, 2021, 35(3): 188-190+201. |
| [4] |
韩维, 崔凯凯, 刘洁, 等. 基于自校正MPC的舰载机着舰控制技术[J]. 系统工程与电子技术, 2022, 44(1): 250-261. |
| [5] |
晋文超, 李鹏, 李亚军, 等. 舰载机起降限制区域及主要影响参数[J]. 中国舰船研究, 2016, 11(5): 28-34. |
| [6] |
朱齐丹, 王立鹏, 张智, 等. 舰载机着舰侧回路时变风险权值矩阵线性变参数预测控制[J]. 控制理论与应用, 2015, 32(1): 101-109. |
 2023, Vol. 45
2023, Vol. 45
