协同导航定位系统的出现,标志着人类太空文明的开始。在国外,较为先进的定位系统有俄罗斯的GLONASSG系统,欧盟的GALILEO,以及美国的GPS系统[1-3]。而我国北斗导航系统(以下简称“北斗系统”)是一种专注于国家安全和社会经济发展,自主创建的20世纪末独立运作的协同导航定位系统。本文以北斗系统为例,以SLAM算法作为辅助手段,通过对无人艇展开相关设计,并将该协同导航定位系统应用其中,分析其导航数据的误差,为后续研究奠定一定理论基础。
1 SLAM算法 1.1 SLAM算法简介要实现无人艇在复杂外部环境中的自主运行,就必须能够在这些复杂场景中安全进行地图绘制和导航。大多数研究学者都认为解决SLAM问题是实现完全自主无人艇控制的关键先决条件,这个问题一直是过去十多年学界研究的重点。
现如今,随着时代的发展以及相关技术的不断进步,SLAM算法得到了较大的提升,可以很好地解决无人艇先前移入环境时位姿预估不可实现等问题。比如有设计人员可以基于无人艇的外形特征、工作环境,以及水域实际运动情况,对无人艇进行针对性的研发,在确保无人艇观察到的信息不被破坏的同时,还可以借助SLAM为无人艇重建全局环境地图,由此引导无人艇得以在安全行驶路径中开展工作[4-6]。
基于以上研究经验,经整理后认为,要想实现SLAM算法的过程,可以按照如图1所示的SLAM思路,将其分为预测和更新2个阶段。

|
图 1 SLAM算法实现过程 Fig. 1 Implementation process of SLAM algorithm |
本文开发了一个基于SLAM程序的完整的无人艇软件系统,以解决无人艇协同导航定位方案和映射任务。
无人艇执行各SLAM任务的联系如图2所示,当无人艇进行协同导航定位和映射任务时,远程无人艇可以在未知环境中使用用户终端PC和键盘进行控制,并显示了各个关键节点与实现无人艇SLAM主题之间的关系。

|
图 2 无人艇执行各SLAM任务的联系 Fig. 2 Connection of Unmanned Craft to Perform Various SLAM Tasks |
在创建无人艇SLAM系统时,本文创建了用于无人艇与客户端末端计算机之间的通信ROS网络。同时在无人艇操作端,也通过PC方式为技术人员提供了节点“/ keyop”、“/ slam_gmapping”和“/ rviz”,方便其工作同时优化硬件配置的影响。此外,每个坐标系之间的坐标变换比率在主题“/ tf”中公布。“/Slam_gmapping”节点订阅“/tf”和“/scan”主题,并基于时变调节因子EKF-SLAM算法,以通过放置无人艇来创建渐变递增的栅格地图。
2 无人艇坐标系模型建立 2.1 无人艇数学模型为无人艇创建SLAM算法问题模型,考虑到由于每个模型的准确性,都将直接影响到SLAM系统的误差评估,从而影响后续的协同导航定位系统性能。因此借助SLAM算法开始部署无人艇时,首先创建3个坐标系,其中无人艇的局部坐标系为X-O-Y,所有坐标系都源于无人艇的原始位置,局部坐标系的坐标位于机体的几何中心。
为了确定无人艇在环境中的位置变化,本文假设其在各种水域中,都可以借助坐标系确定其自身的位置。
如图3所示,在整体的规划思路上,是希望无人艇可以在各种水域中得以移动,将其移动的方向固定为无人艇坐标系X轴方向,然后再将航行角度与X轴的夹角进行计算,得到其在全局坐标系中的位置(x(t),y(t),θ(t))。由于无人艇在各种水域中只存在平动和转动,因此得出以下公式,来表示无人艇在全局坐标系中的位姿。

|
图 3 无人艇数学模型示意图 Fig. 3 Schematic diagram of the mathematical model of an unmanned boat |
| $\left[ \begin{array}{l} {{x(t)}}\\ {{y(t)}}\\ \theta {{(t)}} \end{array} \right] = \left[ \begin{array}{l} x(t - 1) + \Delta d\cos(\theta (t - 1) + \varphi ) + \omega (t - 1)\\ y(t - 1) + \Delta d\sin (\theta (t - 1) + \varphi ) + \omega (t - 1)\\ \theta (t - 1) + \varphi MOD{2^{\text{π}}} + \omega (t - 1) \end{array} \right]\text{。} $ |
按照以上思路设计出来的无人艇,对其运动模型进行构建,可以让无人艇能在短时间内进行受控圆周运动,改变其运动轨迹。不过也有考虑到系统误差,因此在进行运动模型的设计中,依据无人艇的理论运动与无人艇输入控制量,得到运动误差,因此有必要通过合理的计算减小其误差。最终,使用差动驱动对无人艇进行转换编码,得出其增量式编码器△t内的平均速度:
| $ V = \frac{{\Delta {{N}}}}{{{{P}} \times {{n}}}} \times 2 \times {\text{π}} \times {{r}} \times \frac{{\text{1}}}{{\Delta {{t}}}} \text{,} $ |
用l与r分别表示左轮和右轮的速度,则
| $ {V_{{l}}} = \frac{{\Delta {{{N}}_{\text{l}}}}}{{{{p}} \times {{n}}}} \times 2 \times {\text{π}} \times {{r}} \times \frac{{\text{1}}}{{\Delta {{t}}}} \text{,} $ |
| $ {V_{{r}}} = \frac{{\Delta {{{N}}_{{r}}}}}{{{{p}} \times {\text{n}}}} \times 2 \times {\text{π}} \times {{r}} \times \frac{{\text{1}}}{{\Delta {{t}}}} \text{。} $ |
无人艇的合速度可以表示为:
| $ v=\frac{v_{1}+v_{v}}{2} \text{,} $ |
| $ \varpi = \frac{{\varphi - \theta }}{{\Delta {{t}}}} \text{。} $ |
假设在t-1时刻,无人艇的位姿为
按以上思路,可以求出无人艇的线速度v和角速度
| $ R=f \frac{V}{\omega} \text{。} $ |
通过简单的三角关系可以求出圆心的所在位置
| $ \left[ {\begin{array}{*{20}{c}} {{{{x}}_{\text{c}}}} \\ {{y_c}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {x - \dfrac{v}{w}\sin {\theta _{t - 1}}} \\ {y + \dfrac{v}{w}\cos {\theta _{t - 1}}} \end{array}} \right] \text{。} $ |
可知,无人艇的运动模型方程如下:
| $ \left[ {\begin{array}{*{20}{c}} {{{\text{x}}_t}} \\ {{y_t}} \\ {{\theta _t}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\text{x}}_{t - 1}}} \\ {{y_{t - 1}}} \\ {{\theta _{t - 1}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} { - \dfrac{v}{w}\sin {\theta _{t - 1}} + \dfrac{v}{w}\sin ({\theta _{t - 1}} + w\Delta t)} \\ {\dfrac{v}{w}\cos {\theta _{t - 1}} - \dfrac{v}{w}\cos ({\theta _{t - 1}} + w\Delta t)} \\ {w\Delta t} \end{array}} \right] \text{。} $ |
设时刻t无人艇的位置向量为:
| $ {\overline P _{{u}}} = {X_u}\bar i + {Y_u}\bar j + {Z_u}\bar k \text{,} $ |
协同导航定位系统位置的向量为:
| $ {\overline P _{{s}}} = {X_{{s}}}\bar i + {Y_{_{{s}}}}\bar j + {Z_{{s}}}\bar k \text{,} $ |
则无人艇的归一化位置坐标向量为:
| $ {\overline P _{{{us}}}} = {\overline P _{{s}}} - {\overline P _{{u}}} \text{,} $ |
此时无人艇的位置方位仰角为:
| $ {\text{arccos}}\theta = \frac{{{{\bar P}_{{u}}} \cdot {{\bar P}_{{{us}}}}}}{{\left| {{{\bar P}_{{u}}}} \right|\left| {{{\bar P}_{{{us}}}}} \right|}} \text{。} $ |
其中:
| $ {P_u}_s = ({X_u} - {X_s})\bar i + ({Y_u} - {Y_s})\bar j + ({Z_u} - {Z_s})\bar k \text{。} $ |
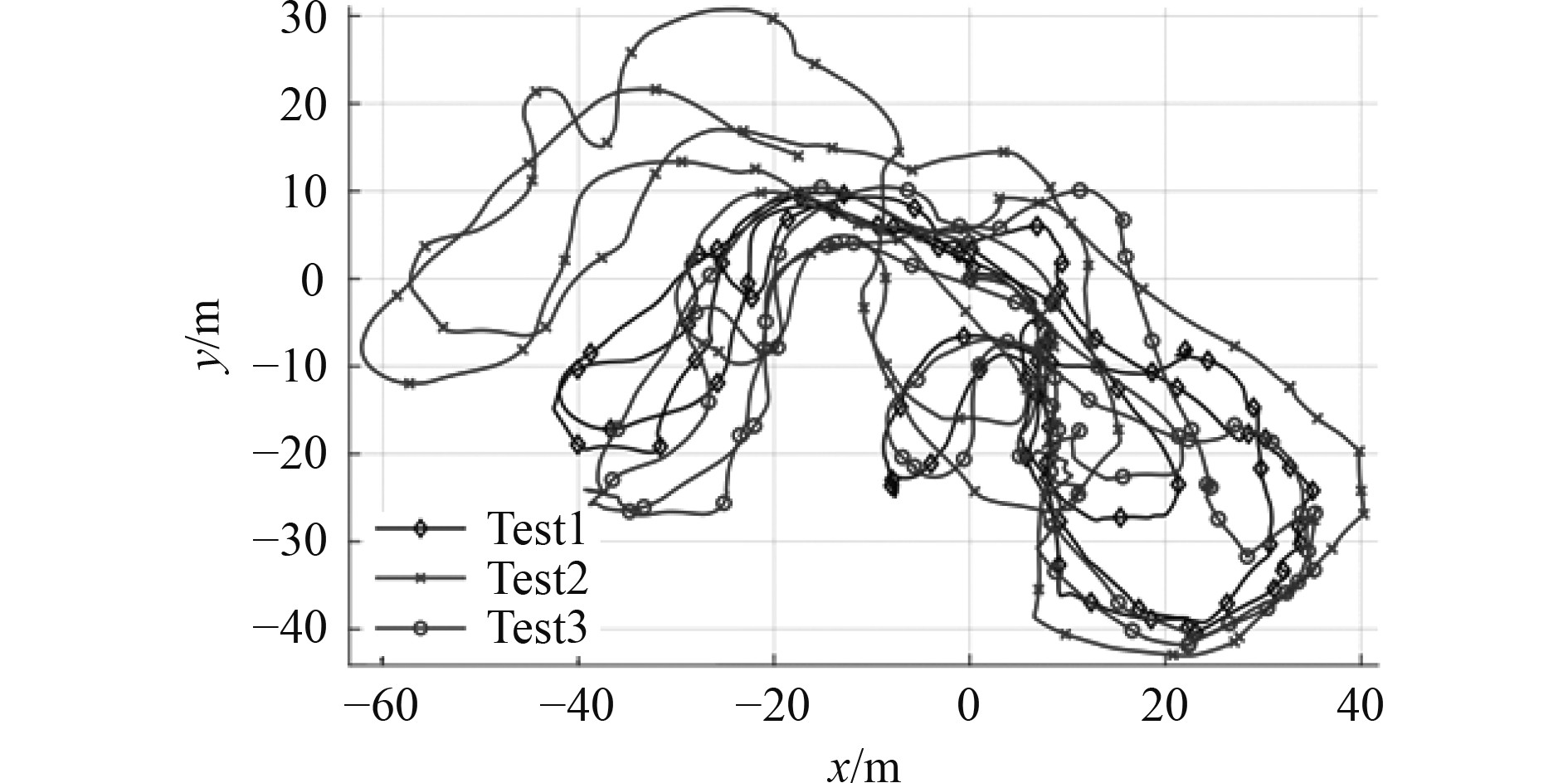
根据以上理论推导,经过仿真计算得:当天可以同时观察到9颗可见协同导航定位系统,对上述的协同导航系统进行3次测试模拟,得到3种测试巡航模式下的航迹分布图如图4所示,可以发现无人艇可以很好对轨迹进行导航和跟踪。
|
图 4 3种测试模式下的航迹分布图 Fig. 4 Track distribution diagrams in three test modes |
根据协同导航定位系统电文提供的轨道参数,按一定的公式可计算出观测瞬间无人艇在坐标系中的位置。具体计算步骤如下:
首先,根据开普勒第三定律,对计算协同导航定位系统运行的平均角速度n进行计算:
| $ {n_0} = \sqrt {\frac{{GM}}{{{a^3}}}} = \sqrt {\frac{\mu }{{{a^3}}}} \text{。} $ |
其中的实际平均角速度为:
| $ n = {n_0} + \varDelta n \text{。} $ |
然后,考虑协同导航定位系统的轨道参数是相对于参考时间的,计算观测时刻的平近点角:
| $ M_k=Mo+nt_k \text{,} $ |
计算偏近点角:
| $ E_k=M_k+e\sin E_k \text{,} $ |
计算真近点角Vk,由于:
| $ \cos {V_k} = \frac{{\cos {E_k} - e}}{{1 - e\cos {E_k}}} \text{,} $ |
| $ \sin {V_k} = \frac{{\sqrt {1 - {e^2}} \sin {E_k}}}{{1 - e\cos {E_k}}} \text{,} $ |
因此:
| $ {V_k} = {\text{arctan}}\frac{{\sqrt {1 - {e^2}} \sin {E_k}}}{{\cos {E_k} - e}} \text{。} $ |
计算升交点角距:
| $ \varnothing k=V_k+w \text{。} $ |
式中,w为导航电文中给出的近地点角距。据此计算摄动改正项:
| $ \left\{ {\begin{aligned} &{{\delta _u} = {C_{uc}}\cos (2{\phi _k}) + {C_{uc}}\sin (2{\phi _k})},\\ &{{\delta _r} = {C_{rc}}\cos (2{\phi _k}) + {C_{rc}}\sin (2{\phi _k})} ,\\ &{{\delta _i} = {C_{ic}}\cos (2{\phi _k}) + {C_{is}}\sin (2{\phi _k})} 。\end{aligned}} \right. $ |
最后,计算协同导航定位系统在轨道平面坐标系的坐标:
| $ \left\{ \begin{aligned} & {{u_k} = {\phi _k} + {\delta _u}} ,\\ & {{r_k} = a(1 - e\cos {E_k}) + {\delta _r}},\\ & {{i_k} = {i_0} + {\delta _i} + {i_{tk}}} 。\end{aligned} \right. $ |
| $ {{X_k}}={{{{r_k}}\cos u_k}} \text{。} $ |
| $ {{Y_k}}={{{{r_k}}\sin u_k}} 。$ |
解算方程写为矩阵形式为:
| $ V=AX-L。$ |
根据观测协同导航定位系统个数,定位解算方程可以分为以下3种情况:
1)当观测量n<4时,无解;
2)当n=4时,AX−L=0,故有唯一解,X=A−1L。
3)当n>4时,方程个数大于未知数个数。此时,可用最小二乘法获得无人艇位置和时间。
本次同时观察到9颗可见协同导航定位系统,因此可以采用最小二乘法对无人艇位置进行定位计算。依照上述的协同导航定位系统坐标,编写程序,设置初始值。高度角:α=10°,采样率:s=10 min。共仿真12 h,仿真结果如表1所示。
|
|
表 1 协同导航定位仿真结果 Tab.1 Simulation results of collaborative navigation and positioning |
通过以上分析,初步计算出“协同导航定位参考点”的位置坐标。为了分析数据误差,再次利用接收机于同一地点得到一组真实的位置坐标数据。通过比较,两者误差如表2所示。
|
|
表 2 误差结果对比 Tab.2 Comparison of error results |
总误差为:
说明该仿真程序能够较为精确的实现对无人艇协同导航定位参考点的定位,达到了设计目的。
4 结 语采用协同导航定位系统的无人艇具有良好的性能,能够满足高精度高速度的作战要求。在协同导航定位技术基础上,取得了较为广泛的应用。
| [1] |
张玉鹏, 王子璇, 刘剑威, 等. 因子图框架下无人艇主从式协同导航算法[J]. 导航定位学报, 2023, 11(2): 131-138. |
| [2] |
庄水管, 翟远钊, 庄哲明, 等. 可重构四足机器人的结构设计与协同导航算法[J]. 科学技术与工程, 2023, 23(1): 256–262.
|
| [3] |
郭鹏军, 张睿, 高关根, 等. 基于相对速度和位置辅助的无人机编队协同导航[J]. 上海交通大学学报, 2022, 56(11): 1438–1446.
|
| [4] |
姜言清, 马东, 李智慧, 等. 北极冰下双自主水下机器人协同地形匹配导航[J]. 哈尔滨工程大学学报, 2022, 43(8): 1091–1095.
|
| [5] |
熊智, 陈芷心, 丁一鸣, 等. 基于分布式协同导航的行人三维惯性SLAM方法[J]. 中国惯性技术学报, 2022, 30(2): 195–201+209.
|
| [6] |
武成锋, 程进, 郭晓云, 等. 飞行器集群协同定位与导航对抗技术发展与展望[J]. 宇航学报, 2022, 43(2): 138–142.
|
 2023, Vol. 45
2023, Vol. 45
