0 引　言

螺旋桨是舰船的主要组成部分^[1]，在舰船航行过程中，为舰船的航行提供动力。螺旋桨通常为多叶片，数量一般为3片或5片。舰船多叶片螺旋桨的角度对于其性能产生直接影响，但舰船航行过程中，受外界环境因素影响，舰船的多叶片螺旋桨角度会产生变化^[2]，为保障舰船多叶片螺旋桨的应用性能，确保舰船正常航行，研究一种有效的舰船多叶片螺旋桨角度调整方法。

陈雷雷等^[3]在研究舰船螺旋桨角度设计问题过程中，基于舰船螺旋桨射流原理与叶片边缘点坐标构建螺旋桨三维模型，通过数值模拟方法完成舰船螺旋桨角度控制。马艳等^[4]在研究舰船螺旋桨角度调整问题过程中，基于螺旋桨材料与水动力性能，结合CFD与有限元相结合的单项流固耦合法实现舰船螺旋桨角度控制。上述方法在研究过程中均未考虑舰船航行过程中所产生的射流扰动问题，因此调度调整结果存在一定偏差，影响螺旋桨应用性能的提升效果。针对上述文献中存在的问题，研究射流扰动下舰船多叶片螺旋桨角度的实时调整方法，希望通过该方法的研究为未来舰船多叶片螺旋桨的设计与应用提供一种全新的、具有较强应用性优化方向与思路。

1 舰船多叶片螺旋桨角度的实时调整方法 1.1 控制方程

舰船多叶片螺旋桨角度的实时调整过程中，采用协同射流控制技术，通过该技术控制射流扰动，经由射流扰动的控制实时调整舰船多叶片螺旋桨角度。协同射流控制技术中的控制方程选用三维雷诺平均N-S方程^[5]，以 $\varPhi$ 表示控制体，利用式(1)能够描述其积分形式的N-S方程：

$\iiint\limits_\varPhi {\frac{{\partial {\boldsymbol{Q}}}}{{\partial t}}}{\rm{d}}V + \iint\limits_{\partial \varPhi } {\overline{\overline A} } \cdot {\rm{d}}{\boldsymbol{S}} = \iint\limits_{\partial \varPhi } {\overline{\overline {{{\boldsymbol{A}}_{\boldsymbol{v}}}}} } \cdot {\rm{d}}{\boldsymbol{S}} 。$

(1)

式中： ${\boldsymbol{Q}}$ 和 $\overline{\overline {\boldsymbol{A}}}$ 分别表示状态矢量和对流通矢量项； ${\boldsymbol{S}}$ 和 $\overline{\overline {{{\boldsymbol{A}}_{\boldsymbol{v}}}}}$ 分别表示舰船螺旋桨单叶片的参考面积和耗散通矢量项。不同项的具体计算公式描述如下：

${\boldsymbol{Q}} = \left\{ \begin{gathered} {\boldsymbol{\rho}} \\ {\boldsymbol{\rho}} u \\ {\boldsymbol{\rho}} v \\ {\boldsymbol{\rho}} w \\ {\boldsymbol{\rho}} R \\ \end{gathered} \right\} ，$

(2)

$\overline{\overline {\boldsymbol{A}}} = \left\{ \begin{gathered} c{\boldsymbol{q}} \\ {\boldsymbol{\rho}} u{\boldsymbol{q}} + c{{\boldsymbol{I}}_{\boldsymbol{x}}} \\ {\boldsymbol{\rho}} u{\boldsymbol{q}} + c{{\boldsymbol{I}}_{\boldsymbol{y}}} \\ {\boldsymbol{\rho}} u{\boldsymbol{q}} + c{{\boldsymbol{I}}_{\boldsymbol{z}}} \\ {\boldsymbol{\rho Hq}} \end{gathered} \right\} ，$

(3)

$\overline{\overline {{{\boldsymbol{A}}_{\boldsymbol{v}}}}} = \left\{ \begin{gathered} 0 \\ {\phi _{xx}}{{\boldsymbol{I}}_{\boldsymbol{x}}} + {\phi _{xy}}{{\boldsymbol{I}}_{\boldsymbol{y}}} + {\phi _{xz}}{{\boldsymbol{I}}_{\boldsymbol{z}}} \\ {\phi _{xy}}{{\boldsymbol{I}}_{\boldsymbol{x}}} + {\phi _{yy}}{{\boldsymbol{I}}_{\boldsymbol{y}}} + {\phi _{yz}}{{\boldsymbol{I}}_{\boldsymbol{z}}} \\ {\phi _{xz}}{{\boldsymbol{I}}_{\boldsymbol{x}}} + {\phi _{yz}}{{\boldsymbol{I}}_{\boldsymbol{y}}} + {\phi _{zz}}{{\boldsymbol{I}}_{\boldsymbol{z}}} \\ {\beta _x}{{\boldsymbol{I}}_{\boldsymbol{x}}} + {\beta _y}{{\boldsymbol{I}}_{\boldsymbol{y}}} + {\beta _z}{{\boldsymbol{I}}_{\boldsymbol{z}}} \end{gathered} \right\} 。$

(4)

式中： ${\boldsymbol{\rho}}$ 和 ${\boldsymbol{q}} = {\left( {u,v,w} \right)^{\rm{T}}}$ 分别表示射流密度和射流流体速度矢量； ${\boldsymbol{Q}}$ 和 $c$ 分别表示射流总能和射流压强； ${\boldsymbol{H}}$ 和 ${{\boldsymbol{I}}_{\boldsymbol{x}}}$ ， ${{\boldsymbol{I}}_{\boldsymbol{y}}}$ ， ${{\boldsymbol{I}}_{\boldsymbol{z}}}$ 分别表示射流总焓和直角坐标系单位坐标向量； $\phi$ 表示直角坐标系内的平面。

同时，针对射流旋转流动，在旋转坐标系下，式(1)等号左侧项还需引入科氏力源项 $\displaystyle\iiint\limits_\varOmega {\boldsymbol{G}}{\rm{d}}V$ ，其公式描述为：

${\boldsymbol{G}} = {\left[ {0,{\boldsymbol{\rho}} {{\left( {w \times {\boldsymbol{q}}} \right)}_x},{\boldsymbol{\rho}} {{\left( {w \times {\boldsymbol{q}}} \right)}_y},{\boldsymbol{\rho}} {{\left( {w \times {\boldsymbol{q}}} \right)}_z},0} \right]^{\rm{T}}}。$

(5)

N-S方程的求解可选取基于格点格式的有限体积法。在模型构建过程中，利用入口与出口的边界条件描述内部泵情况。以增强喷口与吸气口流量分布仿真的准确度为目的，在进口、喷口和出口与吸气口间分别设置弯管网格^[6]，由此降低人工设定速度部分的误差，提升数值模拟准确度。

1.2 协同射流螺旋桨形态受力分析

利用协同射流控制技术控制的舰船多叶片螺旋桨，在承受螺旋桨型物面上气动力影响的同时，还受到吹吸气所产生的反作用力^[7]。 ${P_1}$ 和 ${P_2}$ 分别表示射流出口与入口区域的压力值， ${V_1}$ 和 ${V_2}$ 分别表示射流出口与入口区域的速度值， ${S_1}$ 和 ${S_2}$ 分别表示射流出口与入口区域的面积， ${K_P}$ 和 ${K_V}$ 分别表示影响螺旋桨形态物面上的压力与粘性力所造成的力。以进出口的动量差与静压力之间的相加结果为射流扰动所成型的作用力。依照沿流动方向正方向得到：以 $- \dot m{V_1}$ 和 $- \dot m{V_2}$ 分别表示舰船多叶片螺旋桨气泵出口喷气与入口吸气所产生的反作用力； $- {P_1}{S_1}$ 和 $- {P_2}{S_2}$ 分别表示舰船多叶片螺旋桨气泵出口喷气与入口吸气所产生的压力。由此得到上述力在x方向上的合力计算公式：

${K_x} = \overline{\overline {{H_v}}} \times \left( {{K_{{P_x}}} + {K_{{V_x}}} - {{\left( {\dot m{V_1} + {P_1}{S_1}} \right)}_x} + {{\left( {\dot m{V_2} + {P_2}{S_2}} \right)}_x}} \right) ，$

(6)

利用式(5)描述y方向合力：

${K_y} = \overline{\overline {{H_v}}} \times \left( {{K_{{P_y}}} + {K_{{V_y}}} - {{\left( {\dot m{V_1} + {P_1}{S_1}} \right)}_y} + {{\left( {\dot m{V_2} + {P_2}{S_2}} \right)}_y}} \right)。$

(7)

1.3 喷口动量系数及泵功率计算

利用协同射流控制技术实时调整射流扰动过程中， ${C_\mu }$ 表示舰船多叶片螺旋桨的喷口动量系数，其能够描述喷气量的大小，对于协同射流控制过程产生重要影响。V_j表示舰船多叶片螺旋桨喷口速度，则 ${C_\mu }$ 的计算公式如下：

${C_\mu } = \frac{{\dot m{V_j}K}}{{\dfrac{{{\rho _\infty }V_\infty ^2S}}{2}}}。$

(8)

式中： $\dot m$ 和 $K$ 分别表示射流质量流量和整体合力， ${\rho _\infty }$ 和 $V_\infty ^{}$ 分别表示无穷远区域自由来流密度和速度。

利用式(9)能够描述协同射流控制技术中，舰船多叶片螺旋桨驱动泵的功率消耗情况：

${P_o} = \frac{{\dot m{C_p}{T_0}K}}{\alpha }\left( {{\xi ^{\frac{{\gamma - 1}}{\gamma }}} - 1} \right)。$

(9)

式中：C_p和T₀分别表示定压比热容和总温； $\alpha$ 表示舰船多叶片螺旋桨的气泵效率假设值，通常情况下取值为0.9； $\xi = \dfrac{{{P_{01}}}}{{{P_{04}}}}$ ，其中 ${P_{01}}$ 和 ${P_{04}}$ 表示舰船多叶片螺旋桨的气泵吹气口与吸气口位置的总压； $\varepsilon$ 表示值为1.4的常数值。

舰船多叶片螺旋桨的气泵功率系数为：

$P_C^{} = \frac{{{P_o}}}{{0.5{\rho _\infty }V_\infty ^3S}} 。$

(10)

在实际确定气动效率过程中，需结合气泵的能量消耗。以阻力描述气泵消耗的功率，设定有效阻力与有效阻力系数，公式描述如下：

${D_c} = D + \frac{{Power}}{{V_\infty ^{}}}，$

(11)

${C_{{D_c}}} = {C_D} + P_C^{} 。$

(12)

式中，C_D表示舰船多叶片螺旋桨的阻力系数。

基于上述理论，结合舰船多叶片螺旋桨气泵功率消耗的升阻比^[8]，利用式(13)计算舰船多叶片螺旋桨气泵的有效升阻比：

${\left( {\frac{L}{D}} \right)_c} = \frac{L}{{D + \dfrac{{Power}}{{V_\infty ^{}}}}} 。$

(13)

针对传统的舰船多叶片螺旋桨形态，不具备气泵，也就是能量消耗值为0，由此可将式(13)转换为舰船多叶片螺旋桨形态的气动效率计算公式。

基于上述过程所得喷口动量系数与气泵功率系数等参数，分析这些参数对协同射流的影响，基于这种影响实现舰船多叶片螺旋桨角度实时调整。

2 实验结果与分析

本文研究射流扰动下舰船多叶片螺旋桨角度的实时调整方法，为验证本文方法的应用性能，选取某舰船的多叶片螺旋桨为研究对象，采用本文方法对其进行螺旋桨角度的实时调整测试。测试过程中实验环境为：标准海平面大气环境；风速为15 m/s；迎角为20°±20°。

2.1 功率需求及效能比分析

分析不同迎角条件下，本文方法应用过程中的功率需求与效能比，结果如表1所示。可知，功率的数据模拟结果与数据统计结果基本一致，表明本文方法具有较强的可靠性，由此也能够说明本文方法应用过程中所需的能量较少，具有较高的效能比。值得重点说明的是，增升效能比与减阻效能比的值高于100%并非表示本文方法是“永动机”，只是说明本文方法能够有效解决流场特性问题，提升原射流流动的能量利用率，由此带动效率提升。

2.2 零迎角条件下升力增量与减阻效率

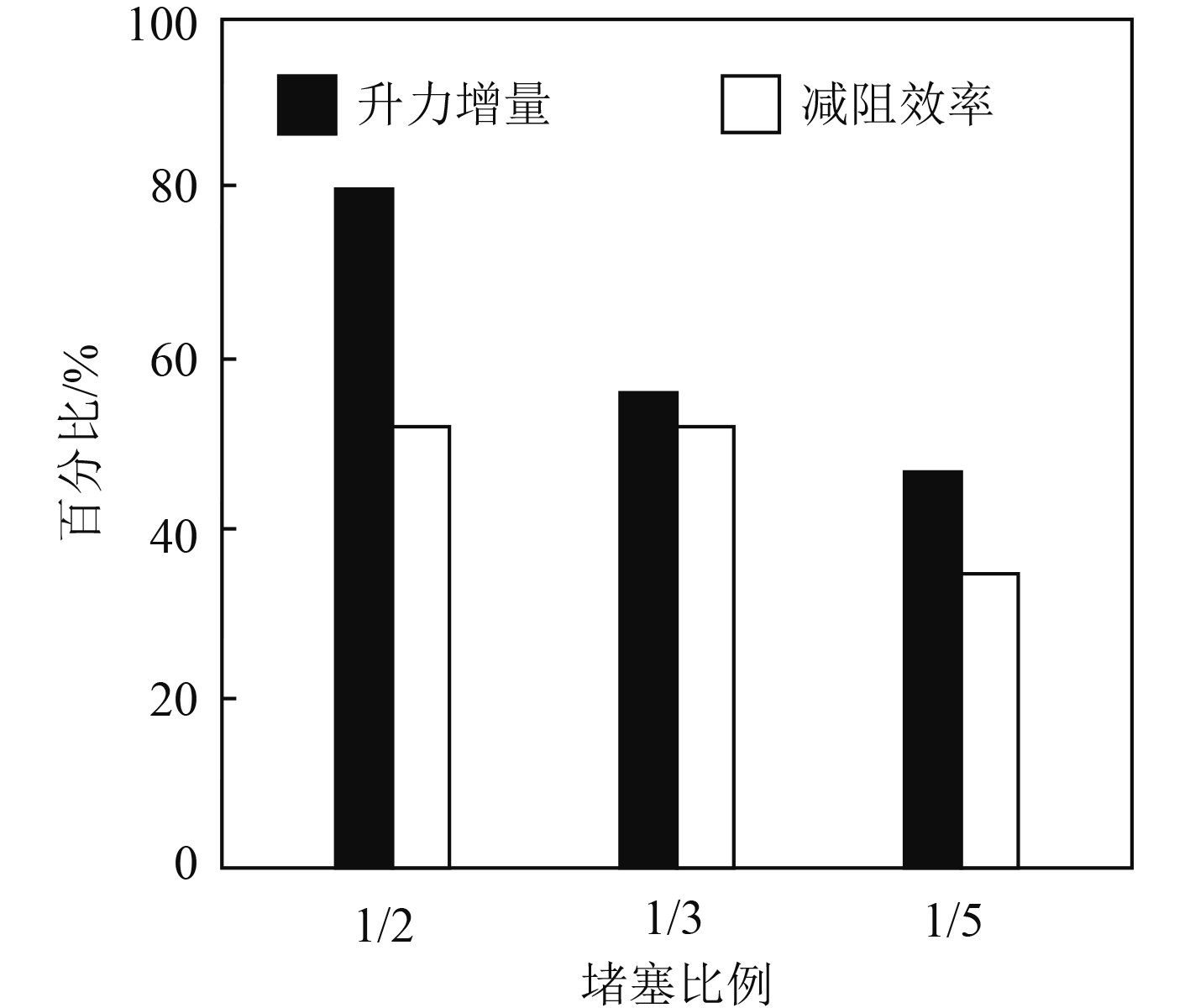
图1为零迎角条件下，本文方法的升力增量与减阻效率。分析可知，对升力增量来说，堵塞比例同增升效果之间具有正比例相关性，也就是增升效果随堵塞比例的提升而提升。对减阻效率来说，堵塞比例同减阻效率之间具有正比例相关性，也就减阻效率是随堵塞比例的提升而提升，但同时效率的功率也有所提升，所以在堵塞比例由1/3提升至1/2的条件下，减阻效率并未继续提升。

2.3 不同方法应用性能对比

为验证本文方法在螺旋桨角度调整方面的应用性能，选取文献[3]中基于螺旋桨三维模型的调整方法和文献[4]中基于CFD和有限元相结合的单向流固耦合调整方法为对比方法，分别获取本文方法与2种对比方法对螺旋桨角度进行调整后，螺旋桨所产生的推力和效率，结果如表2所示。分析可知，3种不同调整方法中，本文方法调整后所形成的推力最高，达到1587.56 N，与2种对比方法相比提升6%以上。同时与基准桨效率相比提升幅度也最高，达到0.590%，与2种对比方法相比提升0.036%以上。以上数据充分说明采用本文方法调整射流扰动下舰船多叶片螺旋桨角度，能够显著提升螺旋桨的性能。

3 结　语

本文研究射流扰动下舰船多叶片螺旋桨角度的实时调整方法，利用协同射频控制技术对射流扰动进行控制，由此实时调整螺旋桨角度。实验结果说明，本文方法能够显著提升螺旋桨的性能。但本文方法的研究也存在一定局限性，在后续研究优化过程中将综合考虑船体阻力以及螺旋桨振动噪声等因素，以提升本文方法的应用性能。