基于MOSSA算法的船载储能系统容量配置多目标优化方法

引用本文

张金磊, 孙俊, 杨祥国, 刘成龙, 王天琪. 基于MOSSA算法的船载储能系统容量配置多目标优化方法. 舰船科学技术, 2023, 45(14): 63-68 复制到剪切板

ZHANG jin-lei, SUN Jun, YANG Xiang-guo, LIU Cheng-long, WANG Tian-qi. Multi-objective optimization method of shipboard energy storage system capacity allocation based on MOSSA algorithm. Ship Science and Technology, 2023, 45(14): 63-68 复制到剪切板

基于MOSSA算法的船载储能系统容量配置多目标优化方法

张金磊, 孙俊, 杨祥国, 刘成龙, 王天琪

武汉理工大学船海与能源动力工程学院，湖北武汉 430063

收稿日期: 2022-05-24.

基金项目: 国家重点研发计划项目(2019YFE0104600)；国家自然科学基金面上项目(52271329)

作者简介: 张金磊(1996-)，男，硕士研究生，研究方向为船舶系统仿真及智能控制

摘要: 当电推船采用储能装置来解决负载扰动带来的船舶微电网稳定性及安全性问题时，储能装置的容量直接影响到船舶电力系统的经济、稳定、可靠性等综合性能指标。以锂电池为储能装置，并对锂电池容量进行多目标协同优化配置。建立以储能系统经济性、微电网稳定性以及锂电池寿命损耗为目标函数的数学模型，采用多目标麻雀搜索算法（MOSSA）对模型进行求解，得到相应的 Pareto解集。通过多目标模糊决策方法，设定不同决策场景，计算综合满意度，获得最终的容量配置方案。

关键词: 船舶电力推进储能系统容量配置 MOSSA

Multi-objective optimization method of shipboard energy storage system capacity allocation based on MOSSA algorithm

ZHANG jin-lei, SUN Jun, YANG Xiang-guo, LIU Cheng-long, WANG Tian-qi

School of Naval Architecture, Ocean and Energy Power Engineering, Wuhan University of Technology, Wuhan 430063, China

Abstract: When the energy storage device is used to solve the stability and safety problems of the ship micro-grid caused by load disturbance, the capacity of the energy storage device directly affects the comprehensive performance index like economy, stability, reliability, etc. of the ship power system. Taking lithium battery as energy storage device, the capacity of lithium battery was optimized with multi-objective coordination. A mathematical model was established with the economy of energy storage system, stability of microgrid and life loss of lithium battery as the objective function. The multi-objective Sparrow search algorithm (MOSSA) was used to solve the model and the corresponding Pareto solution set was obtained. By using multi-objective fuzzy decision making method, different decision scenarios are set, comprehensive satisfaction degree is calculated, and the final capacity allocation scheme is obtained.

Key words: marine electric propulsion energy storage system capacity allocation MOSSA

0 引　言

船舶行业的发展趋势倾向于能耗更低、排放更少的绿色船舶，利用清洁燃料发电机组的电力推进船舶逐渐成为研究热点^[1]。然而，由于航行环境的变化，产生负载波动，进而导致燃料发动机中的空气混合比难以得到精确控制，同时影响船舶微电网的稳定运行^[2]。通过配置储能装置对电力推进船舶的功率波动进行削峰填谷，能够很好地改善这一问题。

目前国内外已有相关文献对储能系统配置在电力推进船舶中展开研究。孙盼等^[3]通过复合储能的形式对船舶负载进行功率平抑，并采用自适应惯性权重粒子群算法对容量进行配置。庞水等^[4]通过锂电池来平抑船舶微电网受功率波动的影响，构建相应的数学模型，采用基于分解的多目标差分进化算法对该模型进行求解，获得储能装置的容量。毛亚洲等^[5]提出为保证船舶电网的安全稳定，利用混合储能技术，利用锂电池与超级电容的相关特性，采用粒子群优化算法对混合储能系统进行容量配置。

上述研究表明，智能优化算法可以实现船载储能装置的容量配置，本文采用将多目标优化机制融合到一种新型群体智能优化算法即麻雀搜索算法，形成多目标麻雀搜索算法（MOSSA），并应用于船载储能装置的容量配置是一种新的设计思路。以某双燃料（LNG-柴油）电推船为例，通过建立储能系统容量配置的优化数学模型，采用多目标麻雀搜索算法（MOSSA）对模型进行求解，在满足功率约束的情况下，通过多目标模糊决策方法，得到最优的容量配置。

1 船载储能系统容量配置多目标优化建模 1.1 优化目标函数

配置储能装置是为了实现平抑船舶微电网的功率波动，将储能系统经济性、微电网稳定性、锂电池寿命损耗作为优化的目标函数。优化锂电池容量时，需要满足船舶电力系统的稳定运行，因此提出相关约束条件。

1.1.1 储能系统经济性目标

经济性目标是在满足船舶稳定航行的基础上尽量减少成本。锂电池的容量大小、单位价格、后期的维护以及能量转化率，构成了储能系统的总成本，因此建立经济性目标函数：

${f}_{1}={C}_{b}{E}_{b}/{\mathrm{\eta }}_{b}+{C}_{m}{P}_{b} 。$

(1)

式中： ${C}_{b}$ 为锂电池单位容量价格； ${E}_{b}$ 为锂电池额定容量； ${\mathrm{\eta }}_{b}$ 为锂电池的能量转化率； ${C}_{m}$ 为储能装置的维护成本； ${P}_{b}$ 为锂电池的额定功率。

1.1.2 船舶微电网稳定性目标

船舶航行过程中，随着工况与运行环境的变化会导致船舶电网功率波动，降低船舶微电网系统的稳定性，通过储能系统平抑后的发电机功率变化差值再进行完全平方和，以此表示储能系统对船舶负载功率变化的平抑效果，建立目标函数：

${f}_{2}=\sum _{i={t}_{1}}^{{t}_{2}}{({p}_{o,i}-{p}_{o,i-1})}^{2} ，$

(2)

${P}_{o,i}'={P}_{o,i}-{P}_{b,i} 。$

(3)

式中： ${t}_{1}$ 和 ${t}_{2}$ 分别为采集数据启末时间点； ${P}_{o,i}^{\mathrm{\text{'}}}$ 为第 $i$ 时间段内通过锂电池补偿之后发电机运行过程中的发出功率； ${P}_{o,i}$ 为实际发电机功率； ${P}_{b,i}$ 为锂电池的输出功率。

1.1.3 锂电池寿命损耗目标

通过相关实验表明，锂电池充放电流波动较大时，会增大动力电池的寿命损耗，因此将锂电池输出功率的波动与额定容量之比作为本文锂电池寿命损耗目标函数：

${f}_{3}=\dfrac{{\displaystyle\sum} _{i={t}_{1}}^{{t}_{2}}{({P}_{b,i}-{P}_{b,i-1})}^{2}}{{E}_{b}} 。$

(4)

1.2 约束条件

对于船载储能系统容量配置优化，在优化目标函数的同时，还要考虑相应的约束条件，本文将能量约束、瞬时功率平衡约束、储能装置中储能单元的荷电状态上下限约束、最大功率限幅作为约束条件，构成多目标优化数学模型，从而保证储能装置容量配置优化的合理性。

1.2.1 能量约束

为了保证船舶微电网运行时的供需平衡，其容量应达到船舶微电网功率变化平抑的最大值。

$\Delta {E}_{b}\geqslant \Delta {E}_{{\rm{max}}}。$

(5)

式中， $\Delta{E}_{{\rm{max}}}$ 为船舶电力推进系统最大负载能量的变化量。

1.2.2 瞬时功率平衡约束

船舶运行中，任意时刻的功率需要保持平衡和稳定状态。

${P}_{o,i}' +{P}_{b,i}={P}_{o,i} 。$

(6)

1.2.3 锂电池荷电状态（SOC）约束

锂电池的过充、过放，即超出相应荷电状态范围，都会增大锂电池的寿命损耗、增加维护成本。

$SO{C}_{{\rm{min}}}\leqslant SO{C}_{i}\leqslant SO{C}_{{\rm{max}}}。$

(7)

式中， $SO{C}_{{\rm{min}}}$ 和 $SO{C}_{{\rm{max}}}$ 分别为锂电池荷电状态的上限和下限。

1.2.4 最大瞬时功率的约束

船舶在运行中出现故障会导致异常工作，因此储能装置输出的总功率需要满足负载瞬时功率变化量的最大需求。

${P}_{b,i}\geqslant \Delta {P}_{{\rm{max}}}。$

(8)

式中， $\Delta {P}_{{\rm{max}}}$ 为最大负载瞬时功率的变化量。

从上述内容可以得出电推船储能装置容量配置的多目标优化数学模型：

$\left\{\begin{array}{l} {f}_{1}={C}_{b}{E}_{b}/{\mathrm{\eta }}_{b}+{C}_{m}{P}_{b}，\\ {f}_{2}={\displaystyle\sum} _{i={t}_{1}}^{{t}_{2}}{({p}_{o,i}-{p}_{o,i-1})}^{2}，\\ {f}_{3}=\dfrac{{\displaystyle\sum} _{i={t}_{1}}^{{t}_{2}}{({p}_{b,i}-{p}_{b,i-1})}^{2}}{{E}_{b}}。\end{array}\right.$

$\left\{\begin{array}{l} \Delta {E}_{b}\geqslant \Delta {E}_{{\rm{max}}}，\\ {P}_{o,i}'+{P}_{b,i}={P}_{o,i} ，\\ SO{C}_{{\rm{min}}}\leqslant SO{C}_{i}\leqslant SO{C}_{{\rm{max}}} ，\\ {P}_{b,i}\geqslant \Delta {P}_{{\rm{max}}}。\end{array}\right.$

2 船载储能装置容量配置多目标优化方法

根据多目标数学模型，可以看出目标函数之间存在一定冲突，且相互制约。例如，降低储能装置的成本而选用较小容量的锂电池，这会增加锂电池的寿命损耗，进而降低锂电池的使用寿命。选用较大容量的锂电池，则会增加储能系统的成本。因此，本文选择多目标麻雀搜索算法（MOSSA）对模型进行求解，获得相应Pareto解集。然后，通过模糊决策方法，进行满意度评价，设定不同场景，在不同场景下，选择满意度最高的方案，获得最终的容量配置。

2.1 多目标麻雀搜索算法（MOSSA）

麻雀搜索算法（Sparrow Search Algorithm，SSA）是一种在2020年提出的具有局部搜索能力强，可调参数较少等优点的智能优化算法^[6]。该算法主要根据麻雀群觅食过程，并且叠加了侦察预警的机制。在麻雀群体中找到食物较好的个体作为发现者，其余个体作为跟随者，同时选择种群中的部分个体进行侦察预警，当发现危险时，则立即放弃所找到的食物，保证安全。

将多目标优化机制融合到麻雀搜索算法中，形成多目标麻雀搜索算法（MOSSA）。为了验证所提算法的有效性，对该算法进行优化测评，同时选取NSGA-II算法，以及MOEAD算法作为对比算法。

为比较不同优化算法的性能，采用反转迭代距离（IGD）评价指标来量化算法的性能。反转迭代距离（Inverted Generational Distance, IGD）是用于均衡真实Pareto前沿与算法所求得的个体集合之间的最小距离^[7]。IGD值越小，则证明该优化算法的分布性和收敛性越好，综合性能更为优越。其评价指标表达式为：

$\mathrm{I}\mathrm{G}\mathrm{D}({A},{B})=\dfrac{{\displaystyle\sum }_{{V}\in {A}}{d}({v},{B})}{\mid {A}\mid }。$

(9)

式中：A是真实的Pareto解集；B为算法所得到的真Pareto最优前沿； ${d}({v},{B})$ 为A中个体v到种群B的最小欧氏距离； $\mid {A}\mid$ 为分布在真实Pareto面上的解集的个数。

标准测试函数能够立体的展示算法得出的结果。本文采用标准测试函数DTLZ(1)和DTLZ(2)对各算法进行优化测评，多目标测试函数DTLZ(1)和DTLZ(2)分别如下式：

DTLZ(1)测试函数

$\left\{\begin{array}{l} \min{f}_{1}\left(x\right)=\dfrac{1}{2}{x}_{1}{x}_{2}...{x}_{m-1}[1+g({x}_{m}\left)\right] ，\\ \min{f}_{2}\left(x\right)=\dfrac{1}{2}{x}_{1}{x}_{2}\dots {(1-x}_{m-1}\left)\right[1+g\left({x}_{m}\right)] ，\\ \min{f}_{m-1}\left(x\right)=\dfrac{1}{2}{x}_{1}(1-{x}_{2}){(1-x}_{2}\left)\right[1+g\left({x}_{m}\right)]，\\ \min{f}_{m}\left(x\right)=\dfrac{1}{2}(1-{x}_{2})[1+g({x}_{m}\left)\right] ，\\ 0\leqslant {x}_{i}\leqslant 1,i=\mathrm{1,2},...,n。\end{array}\right.$

(10)

其中： $g\left({x}_{m)}\right)=100\left\{\right|{x}_{m}|+{\sum }_{{x}_{i}\in {x}_{m}}({({x}_{i}-0.5)}^{2}-\mathrm{cos}\left[20{\text π} \right({x}_{i}-0.5\left)\right]\} 。$

DTLZ(2)测试函数

$\left\{\begin{aligned} &\min{f}_{1}\left(x\right)=[1+g({x}_{m}\left)\right]\mathit{cos}\left(\dfrac{{x}_{1}}{2}\right)...\mathit{cos}\left({x}_{m-2}\dfrac{{\text π} }{2}\right) ，\\ & \min{f}_{2}\left(x\right)=[1+g({x}_{m}\left)\right]\mathrm{cos}\left(\dfrac{{x}_{1}}{2}\right)...\mathrm{cos}\left(\dfrac{{x}_{m-2}{\text π} }{2}\right)\mathrm{s}\mathrm{i}\mathrm{n}\dfrac{{x}_{m-1}\pi }{2}，\\ & \min{f}_{3}\left(x\right)=[1+g({x}_{m}\left)\right]\mathrm{cos}\left(\dfrac{{x}_{1}}{2}\right)...\mathrm{cos}\left(\dfrac{{x}_{m-2}{\text π} }{2}\right)\mathrm{s}\mathrm{i}\mathrm{n}\dfrac{{x}_{m-1}{\text π} }{2}，\\ &\min{f}_{\mathrm{m}}\left(x\right)=[1+g({x}_{m}\left)\right]\mathrm{s}\mathrm{i}\mathrm{n}\dfrac{{x}_{m-2}{\text π} }{2}，\\ &0\leqslant {x}_{i}\leqslant 1,i=\mathrm{1,2},\dots ,n 。\end{aligned}\right.\\[-15pt]$

(11)

其中， $g\left({x}_{m)}\right)={\displaystyle\sum }_{{x}_{i}\in {x}_{m}}({({x}_{i}-0.5)}^{2}。$

其各算法的种群规模大小N = 200，最大迭代次数为T=200。其中MOSSA算法主要参数为发现者初始比例为0.2～0.8，预警麻雀数目10%，预警值为0.8；NSGA-II算法主要参数为交叉概率0.9，变异概率为0.1，MOEAD算法主要参数为目标函数3、变异算子0.5、交叉算子0.3。优化测评结果，IGD评价指标以及运行时间如图1～图6所示。

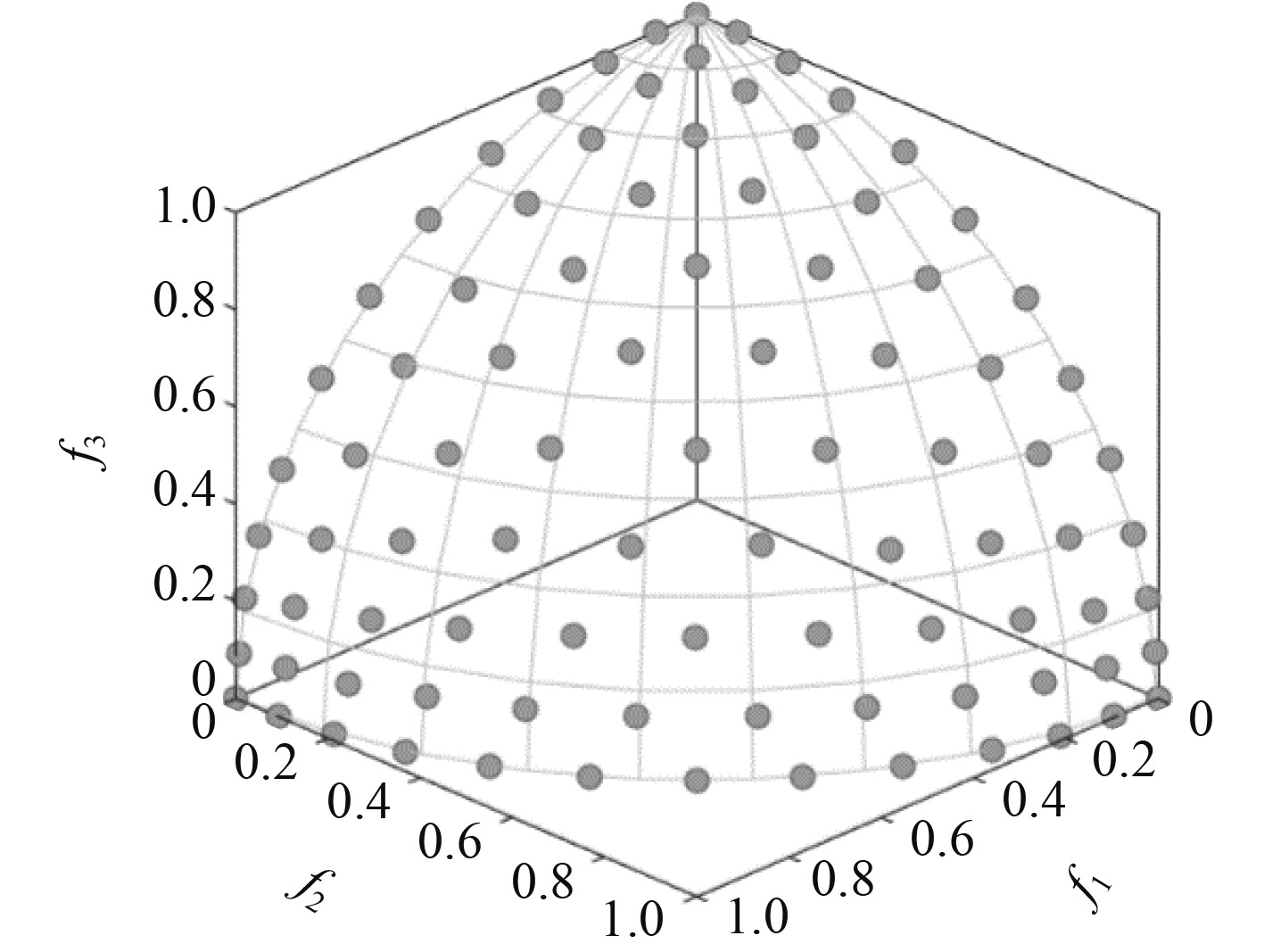
图 1 MOSSA -DTLZ(1) Pareto前沿 Fig. 1 MOSSA - DTLZ(1) Pareto frontier

图 2 MOSSA -.DTLZ(2) Pareto前沿 Fig. 2 MOSSA - DTLZ(2) Pareto frontier

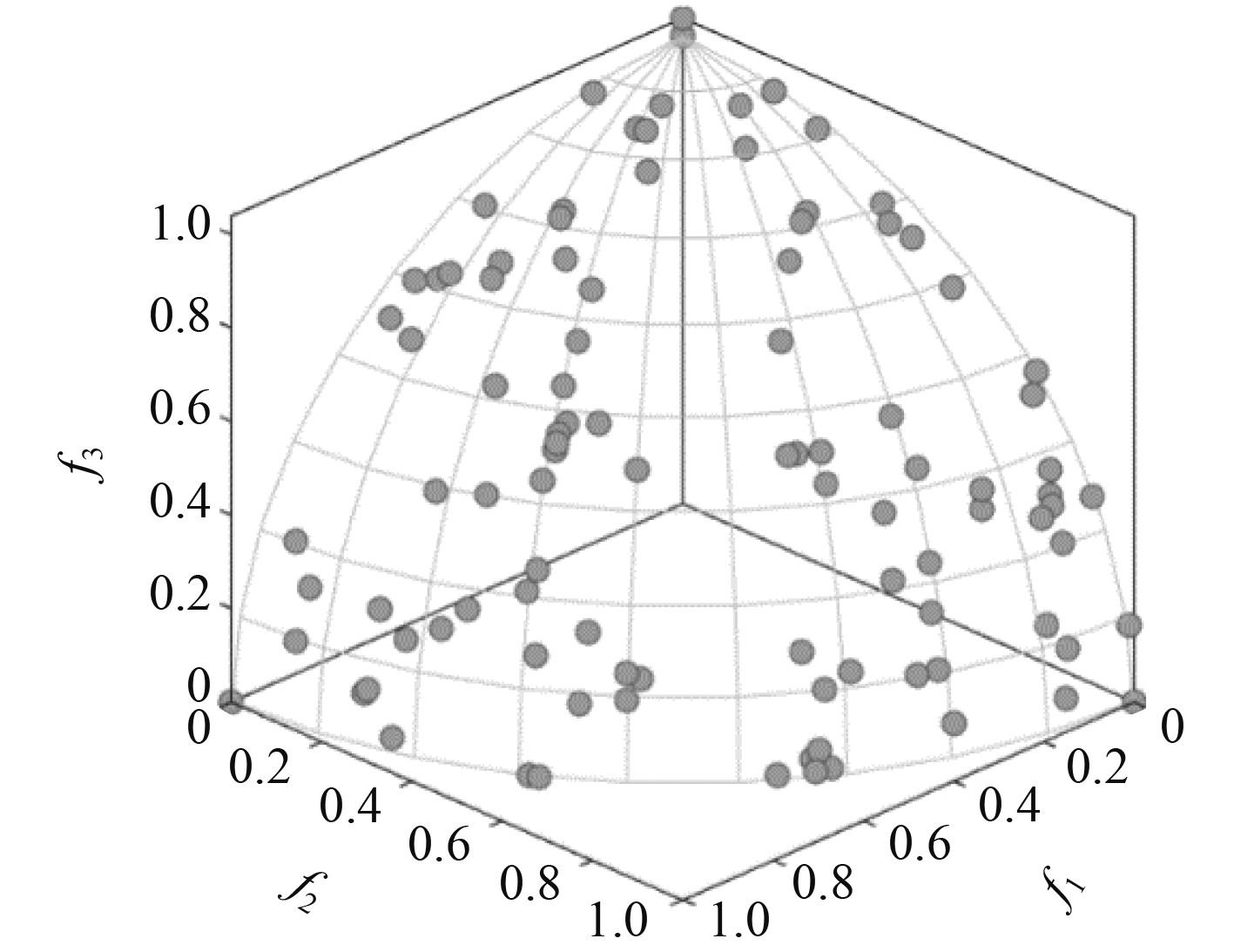
图 3 NSGA-II -DTLZ(1) Pareto前沿 Fig. 3 NSGA-II - DTLZ(1) Pareto frontier

图 4 NSGA-II -DTLZ(2) Pareto前沿 Fig. 4 NSGA-II - DTLZ(2) Pareto frontier

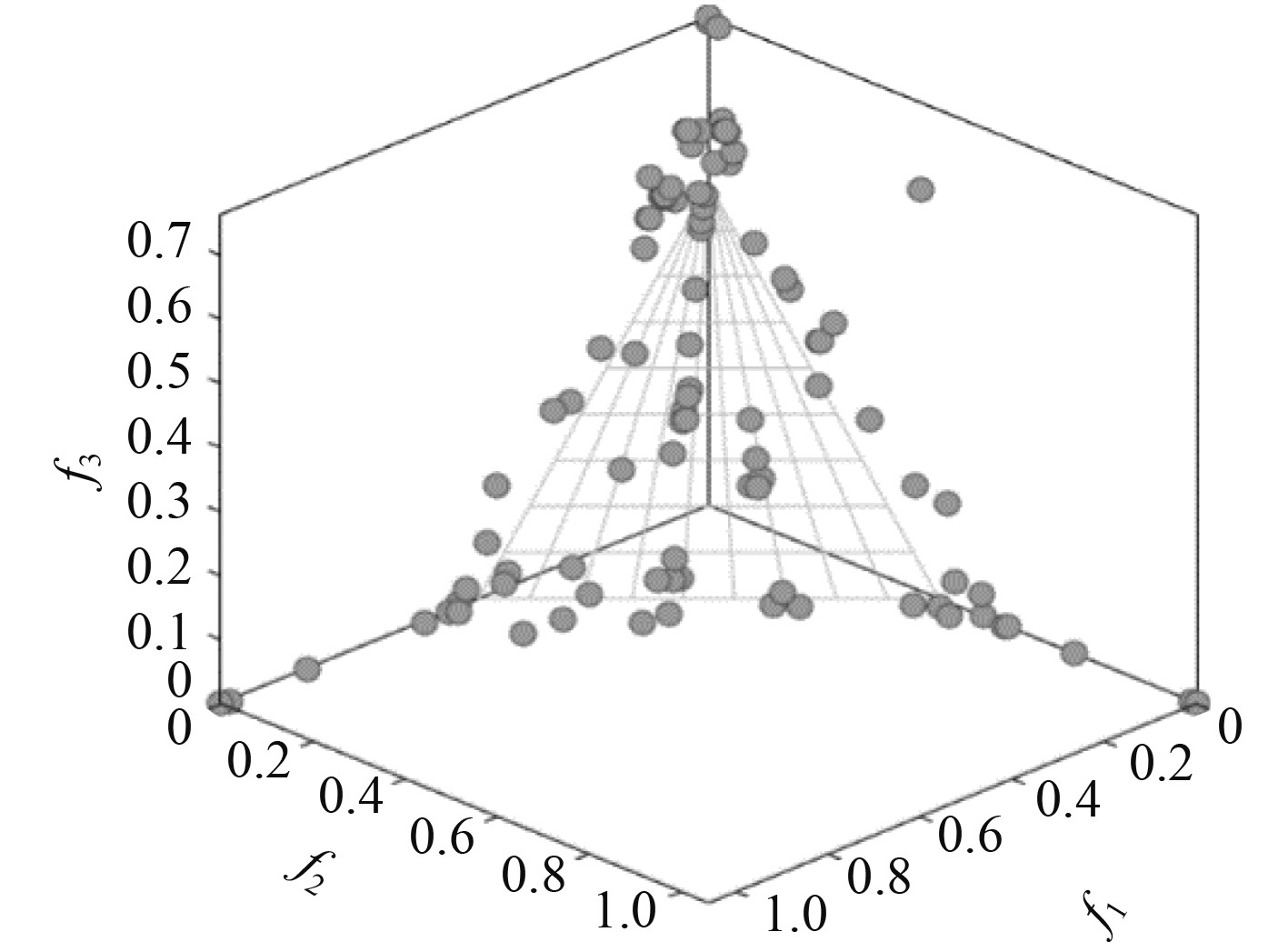
图 5 MOEAD -DTLZ(1) Pareto前沿 Fig. 5 MOEAD - DTLZ(1) Pareto frontier

图 6 MOEAD -DTLZ(2) Pareto前沿 Fig. 6 OEAD - DTLZ(2) Pareto frontier

图1～图6展现出各个算法的收敛和分布形状，在标准函数DTLZ(1)和DTLZ(2)的测试中，MOSSA算法相对于NSGA-II，MOEAD展现了更好的稳定性以及均匀性，从反转迭代距离（IGD）指标中也可以反应出MOSSA算法具有更好的收敛性，各算法运行时间中MOSSA算法收敛速度更快，运行时间更短。实验结果表明，MOSSA 算法能够在多目标测试函数上提供更有竞争力的结果，且具有良好的搜索空间中解的能力，以及更优越的稳定性。因此，选用MOSSA算法作为求解上述数学模型的多目标智能优化算法。

表 1 各算法IGD指标 Tab.1 The wilcoxon rank sum test of IGD

表 2 各算法运行时间 Tab.2 Running time

2.2 多目标模糊决策方法

在获得Pareto 最优前沿结果后，需要对多目标进行决策优选，选择合适的配置方案。使用模糊隶属度函数对实行方案进行满意度评价。其目标函数满意度分别表示为：

${C}_{m}=\left\{\begin{array}{ll} 1\text{，} & {f}_{m}\leqslant {f}_{m}^{\min}，\\ \dfrac{{f}_{m}^{\max}-{f}_{m}}{{f}_{m}^{\max}-{f}_{m}^{\min}} \text{，} &{f}_{m}^{\min}\leqslant {f}_{m}\leqslant {f}_{m}^{\max}，\\ 0 \text{，} & {f}_{m}\geqslant {f}_{m}^{\max}。\end{array}\right.$

(12)

${C}_{m}=\left\{\begin{array}{ll} 1 \text{，}&{f}_{m}\geqslant {f}_{m}^{\max}，\\ \dfrac{{f}_{m}-{f}_{m}^{\min}}{{f}_{m}^{\max}-{f}_{m}^{\min}}\text{，}& {f}_{m}^{\min}\leqslant {f}_{m}\leqslant {f}_{m}^{\max}，\\ 0 \text{，}& {f}_{m}\leqslant {f}_{m}^{\min}。\end{array}\right.$

(13)

因此，储能系统容量配置最优解中各方案的综合性满意度CSA为：

$CS A={a}_{1}{c}_{1}+{a}_{2}{c}_{2} 。$

(14)

式中： ${a}_{1}$ 和 ${a}_{2}$ 为各目标函数在进行评价过程中所对应的权重； ${c}_{1}$ 和 ${c}_{2}$ 则为相应目标函数的满意度。CSA值如果越大，则所选择的方案综合满意度越高，其方案越可靠。

3 计算实例与分析

以某电力推进船舶为实例，由2台中速双燃料（LNG-柴油）发电机组，储能系统由锂电池构成，并通过多端口 DC /DC 变换器与直流母线相连。带储能系统的船舶微电网的结构如图7所示。

图 7 带储能系统的电力推进船舶微电网结构图 Fig. 7 Structure diagram of electric propulsion ship microgrid with energy storage system

锂电池相关参数如表3所示。

表 3 锂电池基本参数 Tab.3 Basic parameters of lithium battery

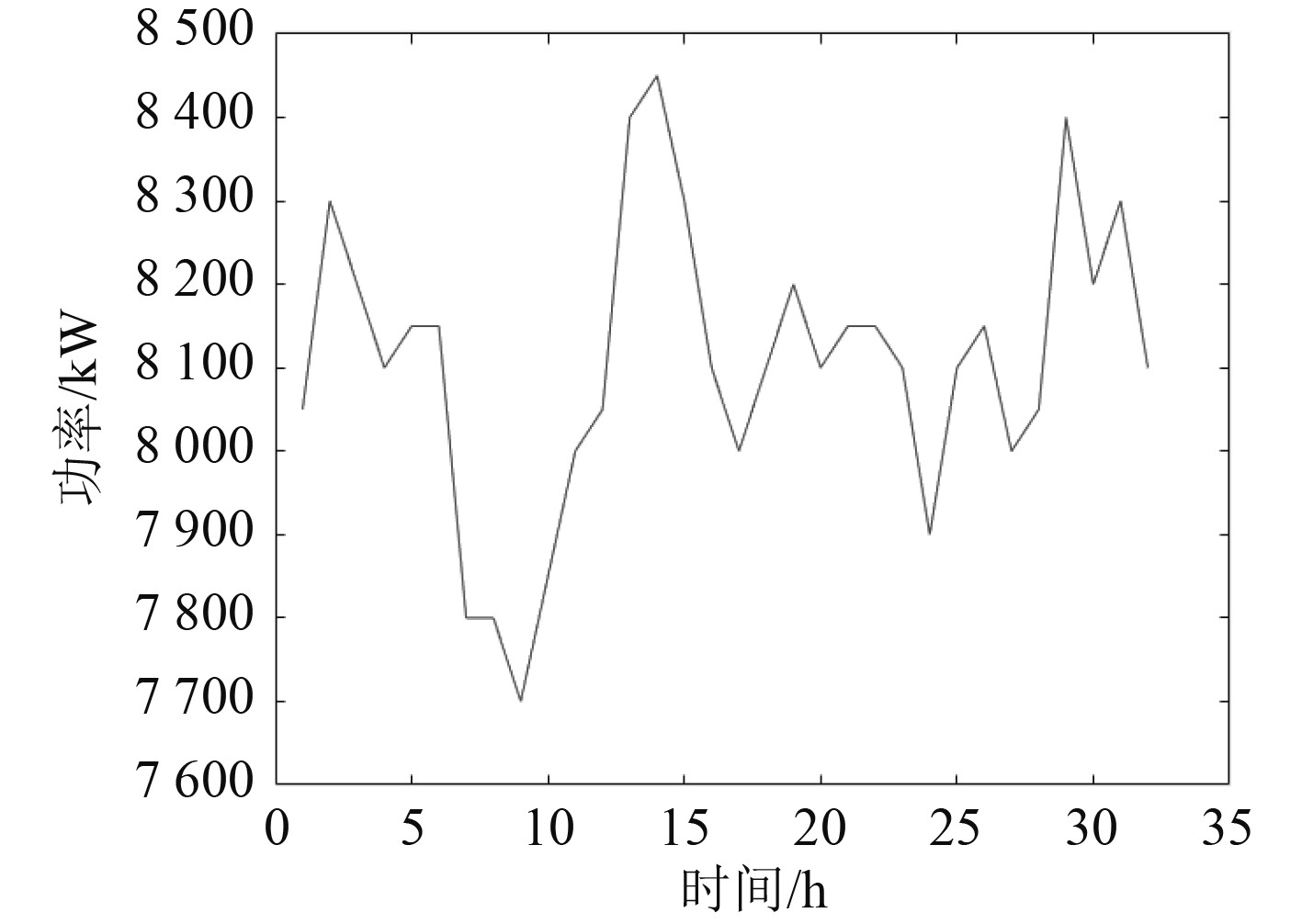
选取该船舶航行中负载波动较大的32 h的数据作为优化数据，其负载变化曲线如图8所示。

图 8 船舶负载 Fig. 8 Ship load

可以看出，该船舶功率变化范围为7600～8500 kW，在航行环境多变的情况下，其负载产生一定的波动，利用功率变化的平均值作为该发电机组的稳定工况点，使用Matlab进行编程，利用MOSSA算法对数学模型进行求解。其MOSSA算法参数：初始化种群大小设置为200，最大迭代次数设置为200，预警值为0.8，发现者初始的比例设置为0.2～0.8，预警麻雀的数目为 $12\%$ ，最优前沿结果如图9所示。

图 9 Pareto前沿图 Fig. 9 Pareto frontiers

可知，由MOSSA算法所得解均可作为该电力推进船舶储能装置容量的解，其解出现在目标函数 ${f}_{2}$ 为0的界面，表明所得到的解满足了平抑微电网功率波动的需求，并且可以计算出锂电池的额定功率值。由于目标函数 ${f}_{2}$ 为0，因此不对 ${f}_{2}$ 进行后续考虑，只对 ${f}_{1}$ 和 ${f}_{3}$ 进行考虑。从Pareto前沿图可以看出，在功率约束满足的情况下， ${f}_{1}$ 储能系统的总费用与 ${f}_{3}$ 锂电池的寿命损耗存在相互冲突，当锂电池容量越大，总费用越高，其寿命损耗越小；当锂电池容量越小，总费用越低，锂电池寿命损耗越大，符合预期逻辑。

从上述最优解集中选出5个方案，进行择优选择，对经济性目标与锂电池寿命损耗目标进行协调规划。储能系统容量配置设计者关于规划方案中经济性目标与锂电池寿命损耗目标的不同要求，进行相应假设，共设置3种场景，从而根据模糊决策的综合满意度，在Pareto最优解集中获取最优规划方案。

假设1　设计者更倾向于锂电池寿命损耗目标，从而减少锂电池的寿命损耗，从Pareto前沿中得到相应方案，取经济性目标权重为0.3，锂电池寿命损耗目标为0.7。

假设2　设计者对经济性目标与锂电池寿命损耗目标需求一致，从Pareto前沿中得到相应方案，取经济性目标权重为0.5，锂电池寿命损耗目标为0.5。

假设3　设计者更倾向于经济性目标，从而减少储能系统成本，从Pareto前沿中得到相应方案，取经济性目标权重为0.7，锂电池寿命损耗目标为0.3。

其最终优化方案如表4所示。

表 4 优化方案 Tab. 4 Optimization scheme

方案	锂电池额定功率/kW	锂电池额定容量/W·h	目标函数f₁	目标函数f₃	假设1 $CSA$	假设2 $CSA$	假设3 $CSA$
1	428	$1.23\times {10}^{6}$	$1.11\times {10}^{7}$	$8.10\times {10}^{-4}$	0.308	0.311	0.668
2	428	$1.79\times {10}^{6}$	$1.23\times {10}^{7}$	$7.12\times {10}^{-4}$	0.380	0.392	0.605
3	428	$2.63\times {10}^{6}$	$1.41\times {10}^{7}$	$6.11\times {10}^{-4}$	0.537	0.558	0.535
4	428	$3.03\times {10}^{6}$	$1.78\times {10}^{7}$	$5.94\times {10}^{-4}$	0.610	0.432	0.403
5	428	$3.53\times {10}^{6}$	$1.97\times {10}^{7}$	$5.05\times {10}^{-4}$	0.652	0.303	0.326

表 4 优化方案 Tab.4 Optimization scheme

可以看出，锂电池的额定功率为一个定值，这是由于目标函数 ${f}_{2}$ 平抑功率优化指标以及相应的功率平衡约束同时限制的作用。在不同的场景下，设计者可以根据优化方案的综合满意度进行选择储能装置的最优容量配置。在假设1的场景，可以选择方案5；在假设2的场景，可以选择方案3；在假设3的场景，可以选择方案1。

4 结　语

本文提出利用储能装置来平抑负载变化带来的功率波动，以锂电池为储能装置，并对锂电池容量进行多目标协同优化配置。建立储能系统的相关数学模型，采用优化效果较好的多目标麻雀搜索算法（MOSSA）对模型进行求解，获得相应 Pareto 最优解集。通过多目标模糊决策方法，设定不同场景，计算相应的综合满意度，选择合适的方案，获得最终的储能系统容量配置方案。本文方法对电力推进船舶储能系统容量配置具有参考意义。

参考文献

[1]	宫宇龙, 陈旭, 陈振东, 等. 论绿色航运双燃料电力推动船舶的发展[J]. 中国水运:下半月, 2013, 13(3): 7+9. GONG Yulong, CHEN Xu, CHEN Zhendong, et al. On green shipping dual fuel electric power promoting the development of ships[J]. China Water Transport: Second Half of the Month, 2013, 13(3): 7+9.
[2]	BO T I , VAKTSKJOLD E , PEDERSEN E , et al. Model predictive control of marine power plants with gas engines and battery[J]. IEEE Access, 2019: 15706-15721.
[3]	杨祥国, 孙盼, 杨诚, 等. 电力推进船舶复合储能装置容量多目标优化[J]. 中国航海, 2018, 41(2): 9-14+62. YANG Xiangguo, SUN Pan, YANG Cheng, et al. Multi-objective optimization of the capacity of composite energy storage devices for electric propulsion ships[J]. Chinese Navigation, 2018, 41(2): 9-14+62. DOI:10.3969/j.issn.1000-4653.2018.02.003
[4]	庞水, 杨楚平, 刘如磊, 等. 船舶微电网锂电池储能系统容量配置多目标优化方法[J]. 中国舰船研究, 2020, 15(6): 22-28. PANG Shui, YANG Chuping, LIU Rulei, et al. Multi-objective optimization method for capacity configuration of lithium battery energy storage system in marine micro grid[J]. Chinese Journal of Ship Research, 2020, 15(6): 22-28. DOI:10.19693/j.issn.1673-3185.01769
[5]	毛亚洲, 俞孟蕻. 混合储能技术在船舶电网中的应用[J]. 舰船科学技术, 2018, 40(13): 96-100+105. MAO Yazhou, YU Menghong. Application of hybrid energy storage in ship power grid[J]. Ship Science and Technology, 2018, 40(13): 96-100+105. DOI:10.3404/j.issn.1672-7649.2018.07.017
[6]	XUE J, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering An Open Access Journal, 2020, 8(1): 22-34.
[7]	JIANG S, YANG S. An Improved multiobjective optimization evolutionary algorithm based on decomposition for complex pareto fronts[J]. IEEE Transactions on Cybernetics, 2017, 46(2): 421-437.


舰船科学技术 2023, Vol. 45 Issue (14): 63-68 DOI: 10.3404/j.issn.1672-7649.2023.14.011	PDF