海上浮动式核电平台采用了较多的用汽设备,具有汽-水循环系统复杂、多参数耦合性强、控制对象多、不同负荷工况下系统响应特性差别大等特点。在实际应用中,浮动式核电平台面对不同用户需求与不同复杂海况,在保证核动力装置安全运行的同时,还需要保证平台具有快速变负荷能力[1],这给核动力装置的控制系统设计带来了较大困难。因此,在快速变负荷条件下,如何灵活稳定地控制主汽发转速成为了研究热点[2-4]。
国内外对汽轮机转速的快速稳定控制进行了大量研究。孙建华[5]为达到使汽轮机转速得到稳定控制的同时又能快速地跟踪其转速的目的,同时利用2种控制方法,将传统PID控制的稳定性与模糊控制的快速响应能力相结合,取得良好效果。苏杰[6]在蒸汽轮机的转速控制过程中使用了广义预测自校正控制算法,与传统PID控制相比,此方法的控制效率更高,系统对控制响应速度更快。雷世雄[7]在汽轮机转速控制中运用了模糊控制方法,同样也使系统对汽轮机转速达到了稳定控制与快速响应跟踪能力。以上关于汽轮机转速控制方面的研究主要是讨论各个控制策略的设计与优化或是采用新的控制方法,但关于控制参数的讨论并不多见,本文进行强耦合系统用汽设备转速控制参数优化研究。
1 汽轮机转速振荡分析进行某海上浮动式核电平台主汽发自动控制试验时,发现汽轮机转入自动后,再引入一定转速偏差的扰动,汽轮机转速等系统运行参数不能恢复到稳态,而是存在一定程度的振荡,并有缓慢发散的趋势,采取改变汽轮机转速调控死区和汽轮机进汽阀门调控精度等措施后,低负荷工况下参数振荡幅度有所缓解,但是在高负荷工况下效果不明显,参数还是存在不可接受的振荡。查看负荷吸收装置(水力测功器)的相关运行数据,发现在进出水阀位不变条件下,汽轮机增加相同转速,所需功率的变化幅度小于理论值功率变化幅度,汽轮机减小相同转速所需功率的变化幅度,也小于理论值功率变化幅度。因此,在阀位不随动的条件下,当出现汽轮机转速波动时,测功器自身抑制阀门波动的类“自稳”能力会变弱。受制于测功器自身响应时间长等特性,阀门实时随动难以实现,一般需要通过对应的转速控制系统参数优化,来保证系统运行稳定性。本文根据上述分析结果建立海上核电平台-汽水循环系统仿真模型,并进行不同工况、不同参数的仿真计算。
2 模型建立 2.1 仿真软件介绍系统运行分析仿真模型的开发在仿真支撑平台软件SimExec基础上进行,采用语言是Fortran。软件代码的建立分为手工编写代码和自动生成代码。系统如二回路主系统和一回路辅助系统(压力安全系统、余热排出系统)的仿真软件采用Jtopmeret自动生成代码。SimExec、Jtopmeret是美国GSE公司(Global Simulation Engining Co.)的仿真软件产品,此软件为一款图形可视化的自动建模软件,主要应用于动态数据监控与大型自动化建模[8],SimExec是通用仿真支撑平台软件,Jtopmeret是两相(气/液)或多组分流体网络仿真建模工具软件[9],Jtopmeret根据Retact的守恒方程,并且兼顾了仿真对实时性的要求,简化了方程,使二回路系统仿真精度得到提升。
2.2 模型构成海上浮动式核电平台由于受到船体空间的限制,其在设备配置、布置与运行等方面与核电站和常规电站有所区别,所以在对浮动式核电平台-汽水循环系统进行仿真时需要注意其系统的复杂性、设备的多样性,存在多工况转换需求所致的复杂水利热工过程响应,以及汽、液两相流动模型等。
浮动式核电平台-汽水循环系统的仿真模型主要包括:蒸汽、凝给水等主要系统和主汽发、辅汽发、蒸汽发生器、凝汽器、凝水泵、汽水分离器、除氧器、给水泵等主要设备模块,以及耦合功率控制、给水流量控制、冷凝器水位控制、冷凝器真空控制、蒸汽排放控制等过程控制模块。
2.3 汽-水循环系统仿真模型建立根据功用及相互关系将系统内设备附件分为几个模块,各模块通过接口参数对接。对每个模块建立不可凝气体质量方程,汽、液质量方程,汽、液动量方程,汽、液能量方程。
1)质量守恒方程
在闭合管道中的流动连续方程如下:
| $ {A}\frac{{\partial \left({\alpha }{\cdot}{\rho }\right)}_{{n}}}{\partial {t}}+\frac{\partial {{F}}_{{n}}}{\partial {Z}}=\sum \frac{\partial {{F}}_{{b}{n}}}{\partial {Z}}+\frac{{\partial {\varGamma }}_{{n}}}{\partial {Z}} 。$ | (1) |
式中:A为流通截面积,m2;α为单相流体占两相流体的体积份额;ρ为流体密度,kg/m3;F为流量,kg/s;Γ为相间质量交换,kg/s。
| $ {{\varGamma }}_{{f}}={{F}}_{\mathrm{b}\mathrm{o}\mathrm{i}\mathrm{l}}-{{F}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}}\pm {{F}}_{\mathrm{r}\mathrm{x}\mathrm{n}}。$ | (2) |
式中:Fboil为蒸发质量变化量,kg/s;Fcond为凝结质量变化量,kg/s;Frxn为化学反应质量变化量,kg/s。
封闭体积节点n内部的组分k的质量平衡,有下式:
| $ \frac{{\mathrm{d}{M}}_{{n},{k}}}{\mathrm{d}{t}}=\sum {{x}}_{\mathrm{i}\mathrm{n},{k}}\cdot{F}_{{n},\mathrm{i}\mathrm{n}}-\sum {x} 。$ | (3) |
2)能量守恒方程
流体能量平衡方程如下:
| $ \begin{split} & A\cdot\frac{{\partial {{\left( {\alpha \cdot \rho \cdot h} \right)}_f}}}{{\partial t}} = - \frac{{\partial {{\left( {h \cdot F} \right)}_f}}}{{\partial Z}} + \\ & A\cdot \left( {\varGamma \cdot{h_{{\rm{sat}}}} + \mathop Q\limits - W} \right) + \sum \partial \cdot{h_s}\cdot{F_{{bn}}}。\end{split}$ | (4) |
式中:α为流体的体积份额;A为横截面积,m2;h为流体焓值,kJ/kg;ρ为流体密度,kg/m3;F为流体流量,kg/s;Γ为相间质量交换,kg/s;hs为饱和焓,kJ/kg;Q为传热量,W;W为外界做功,W;δ为δ函数,等于0或1;hs为边界流体焓,kJ/kg;Fbn为边界流量,kg/s。
也可写为:
| $ \begin{split} & \frac{{{\rm{d}}\left( {{M_f}\cdot{h_f}} \right)}}{{{\rm{d}}t}} = \sum {{h_{f,{\rm{in}}}}} \cdot{F_{f,{\rm{in}}}} - {h_{f,{\rm{out}}}}\cdot{F_{f,{\rm{out}}}} + {\varGamma _f}\cdot{h_{f,{\rm{sat}}}} + \\ & \quad {Q_f} - {W_{{\rm{shaf}}t}} + {V_f}\cdot\frac{{{\rm{d}}P}}{{{\rm{d}}t}} + \frac{{A\cdot{v_f}}}{{Ln}}\cdot{\rm{d }}P。\\[-15pt] \end{split}$ | (5) |
在每一个节点中气相和液相的平衡都是分开计算的。换热项分为向其他相的换热、向热板的换热、额外的热源。
| $ {{Q}}_{{f}}=\pm {{Q}}_{\mathrm{i}\mathrm{n}\mathrm{t}}+\sum {{Q}}_{\mathrm{s}\mathrm{l}\mathrm{a}\mathrm{b}}+\sum {{Q}}_{\mathrm{e}\mathrm{x}\mathrm{t}} 。$ | (6) |
汽轮机的轴功率在汽轮机节点中计算。
3)动量守恒方程
动量平衡方程如下:
| $ \begin{split} & \frac{{{\rm{d}}{F_f}}}{{{\rm{d}}t}} = - \frac{{{\alpha _f}\cdot A}}{{Ku}}\cdot\left( {\frac{{{\rm{d}}P}}{{{\rm{d}}Z}} + {f_{f - w}} + {f_{f - f}} + Ku\cdot{\rho _f}\cdot g - \delta \cdot{P_{\rm{pump}}}} \right) + \\ & \quad \quad \sum \delta \cdot{S_f}\cdot{\overrightarrow v _{src}}。\\[-15pt] \end{split}$ | (7) |
式中:Ff为流体流量,kg/s;αf为流体的体积份额;A为横截面积,m2;Ku为单位转化系数;ff-w为流体对壁面的摩擦因子,N/m3;P为节点压力,Pa;ff-f为流体对流体的摩擦因子,N/m3;g为重力加速度,m/s2;ρf为流体密度,kg/m3;Fbn为边界质量流量,kg/s;Ppump为泵的压头,Pa;νsrc为边界流速,m/s;δ为δ函数,等于0或1。
2.4 汽轮机转速控制模型机组的发电频率取决于汽发的转速,浮动式核电站需根据外部需求控制发电频率,不允许出现较大波动。为使其满足在变负荷条件下始终稳定保持在运行要求所需达到的状态,必须对汽轮机转速进行有效控制[10]。本文使用传统PID控制算法对汽轮机转速进行控制,PID控制原理图如图1所示。
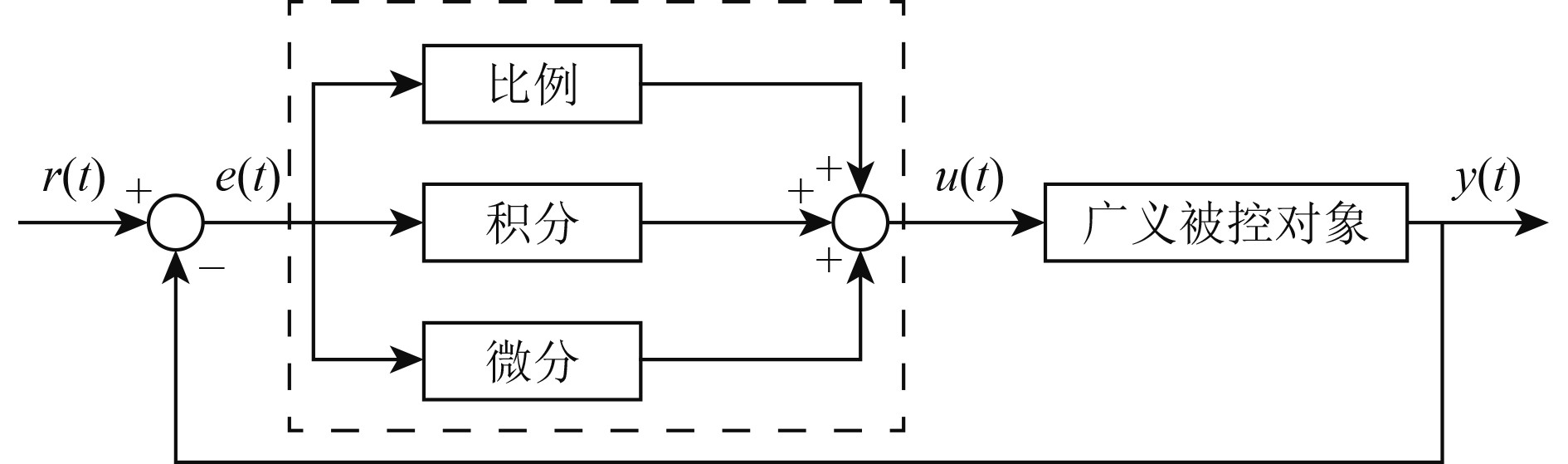
|
图 1 PID控制原理图 Fig. 1 PID control schematic diagram |
虽然转速PID控制具有“自稳”能力,但机组输出的频率是根据外界用户需求所决定的,所以要保证二者的一致性,这也是转速控制系统的功能。
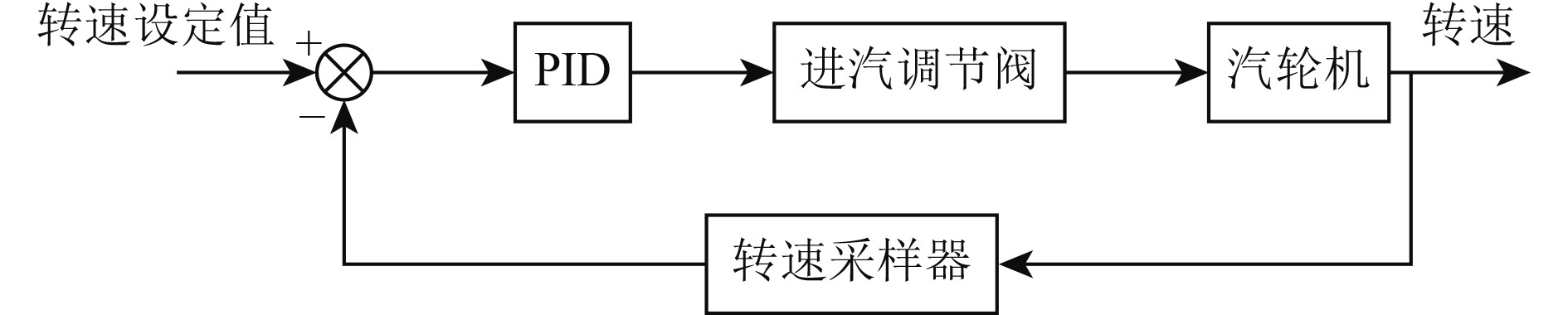
|
图 2 汽轮机转速控制系统原理图 Fig. 2 Turbine speed control system schematic diagram |
为分析改变比例调节参数与积分调节参数对汽轮机转速调控的影响,本文从控制变量角度出发,从以下3个方面进行仿真分析:
1)不同工况下,输入同一组比例、积分调节参数对汽轮机转速调控的影响;
2)相同工况下,积分调节参数不变,不同比例调节参数对汽轮机转速调控的敏感性分析;
3)不同工况下,同一比例调节参数、不同积分调节参数对汽轮机转速调控的敏感性分析。
为直观体现汽轮机转速调控的变化趋势,后续分析中的相关参数均根据实际数值进行归一化处理。
3.1 调控参数对汽轮机转速调控的影响分析在不同工况下,输入同一组P、I调节参数后,汽轮机转速变化如图3所示。

|
图 3 工况2、工况3中P=0.5、I=0.1汽轮机转速变化 Fig. 3 Working conditions 2 and 3, P= 0.5, I =0.1 turbine speed change |
可知,在输入比例调节参数为0.5,积分调节参数为0.1时,不同工况下汽轮机转速调控的稳定性有较大区别。采用该组调节参数,工况2运行时汽轮机转速在引入扰动后能够较快收敛而稳定,显示出较好的控制效果;工况3运行时汽轮机转速在引入扰动后则存在持续振荡而不能稳定。由此可以假设,在不同工况内汽轮机转速均保持相对稳定状态下,可通过改变调节参数来对汽轮机转速进行有效控制。
3.2 汽轮机转速对比例调节参数的敏感性分析系统保持工况3状态运行时,采用2个跨度较为明显的比例调节参数,在引入扰动后,汽轮机转速变化如图4所示。

|
图 4 工况3中I=0.02、P=0.5与0.2汽轮机转速 Fig. 4 Working condition 3, I=0.02, P=0.5 and 0.2 turbine speed |
可知,在比例参数输入为0.5和0.2时,汽轮机转速均发生振荡,且2个曲线的振荡幅度与振荡周期十分接近。由此可推断在保持比例参数不变的条件下,仅改变积分参数对汽轮机控制的效果基本不会产生影响,因此可以忽略比例参数对汽轮机转速控制的影响,进而探讨积分控制参数对汽轮机转速控制效果的作用。
3.3 汽轮机转速对积分调节参数的敏感性分析为了解积分调节参数对汽轮机转速控制的影响,就不同工况采用不同积分调节参数分别展开分析(以下分析均将比例控制参数固定输入为0.5情况下进行讨论)。改变积分调节参数对汽轮机在工况2状态下的转速控制效果如图5~图7所示。
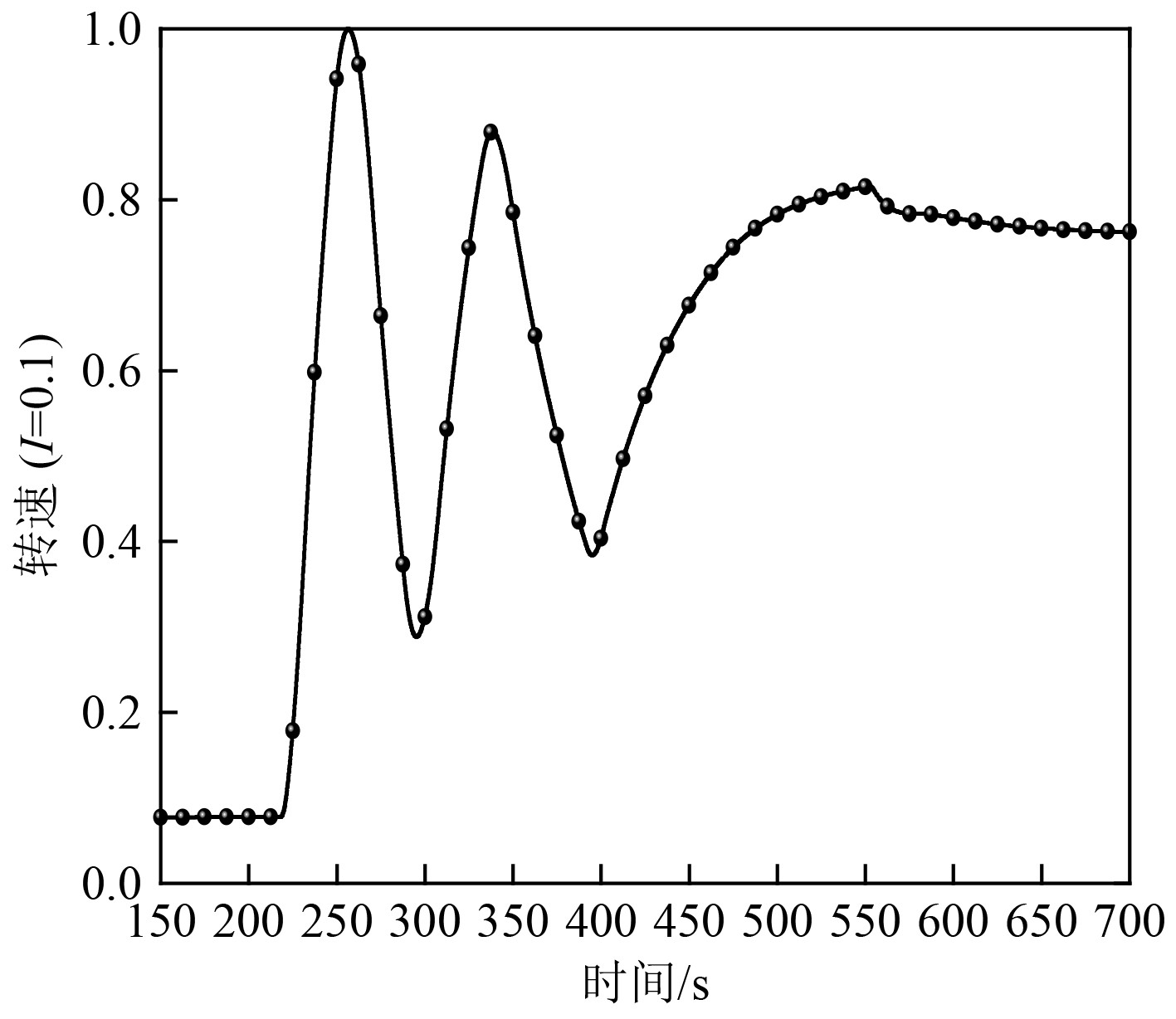
|
图 5 工况中2P=0.5、I=0.1汽轮机转速变化 Fig. 5 Working condition 2, P= 0.5, I =0.1 turbine speed change |
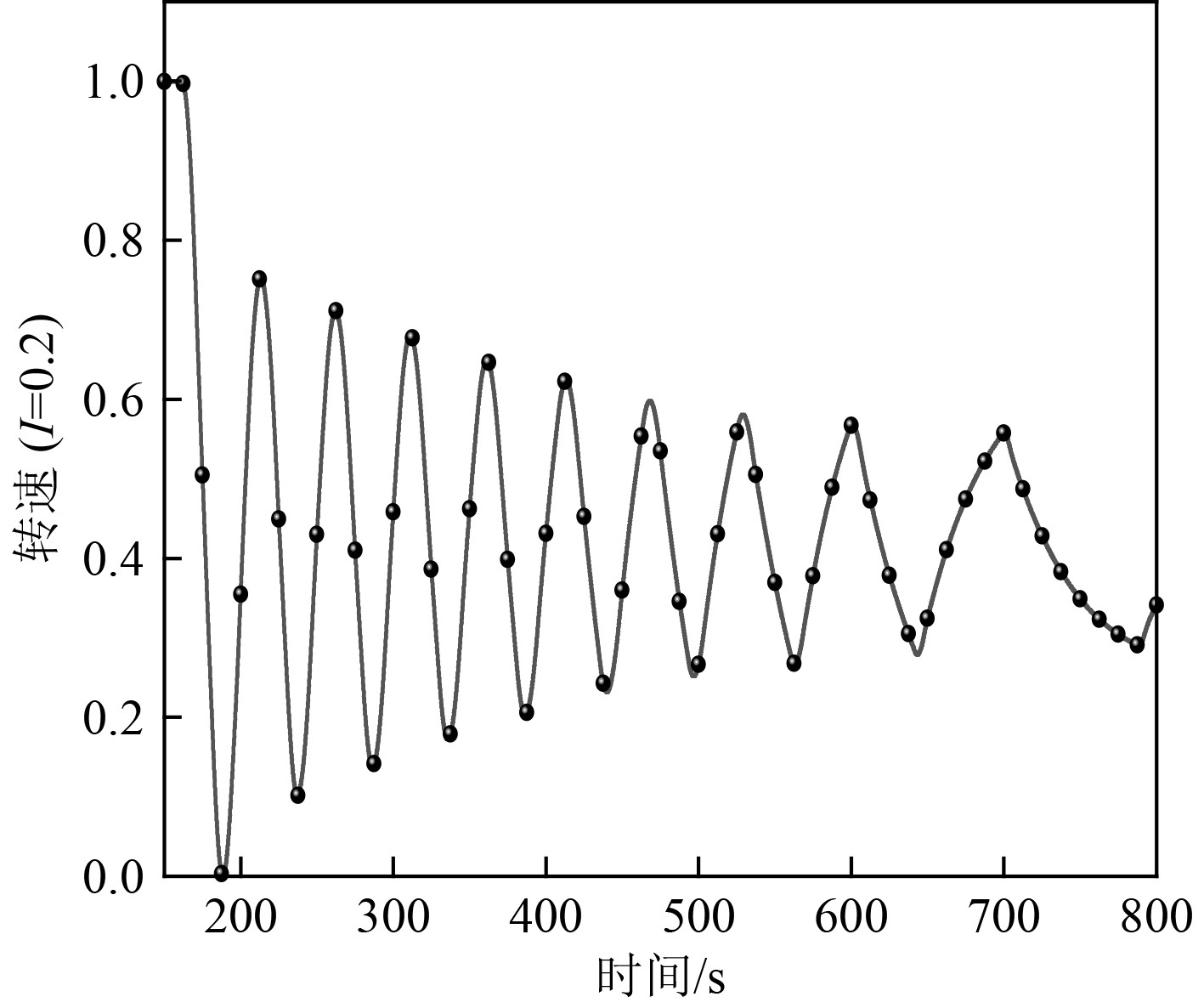
|
图 6 工况2中P=0.5、I=0.2汽轮机转速变化 Fig. 6 Working condition 2, P= 0.5, I =0.2 turbine speed change |
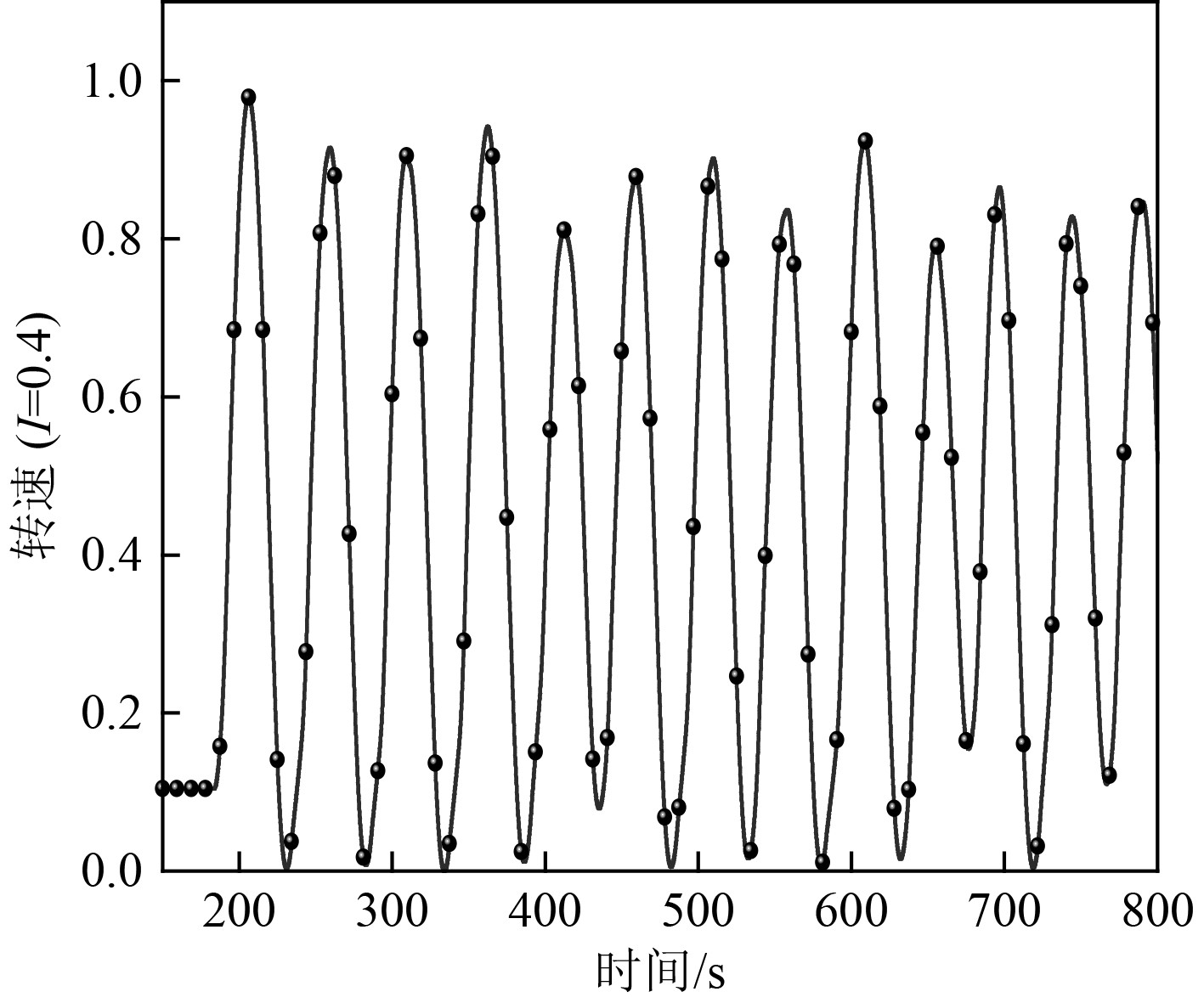
|
图 7 工况2中P=0.5、I=0.4汽轮机转速变化 Fig. 7 Working condition 2, P= 0.5, I =0.4 turbine speed change |
可知,工况2运行时积分参数从0.4到0.1递减,系统运行逐渐稳定。I=0.4时汽轮机转速数在一个较大区间持续振荡,系统处于一个极不稳定的状态。I=0.2时,随着时间变化汽轮机转速振荡幅度越来越小,需长时间才能渐趋于稳定运行状态。I=0.1时,系统在两次振荡之后逐步趋于稳定,并长时间处于稳定运行状态,反映出一定自适应性。因此,分析得出改变积分参数的输入可有效控制系统运行稳定性,且积分参数输入值越小系统越稳定。
改变积分调节参数对汽轮机在工况3状态下的转速控制情况如图8~图10所示。

|
图 8 工况3中P=0.5、I=0.1汽轮机转速变化 Fig. 8 Working condition 3, P= 0.5, I =0.1 turbine speed change |

|
图 9 工况3中P=0.5、I=0.02汽轮机转速变化 Fig. 9 Working condition 3, P= 0.5, I =0.02 turbine speed change |
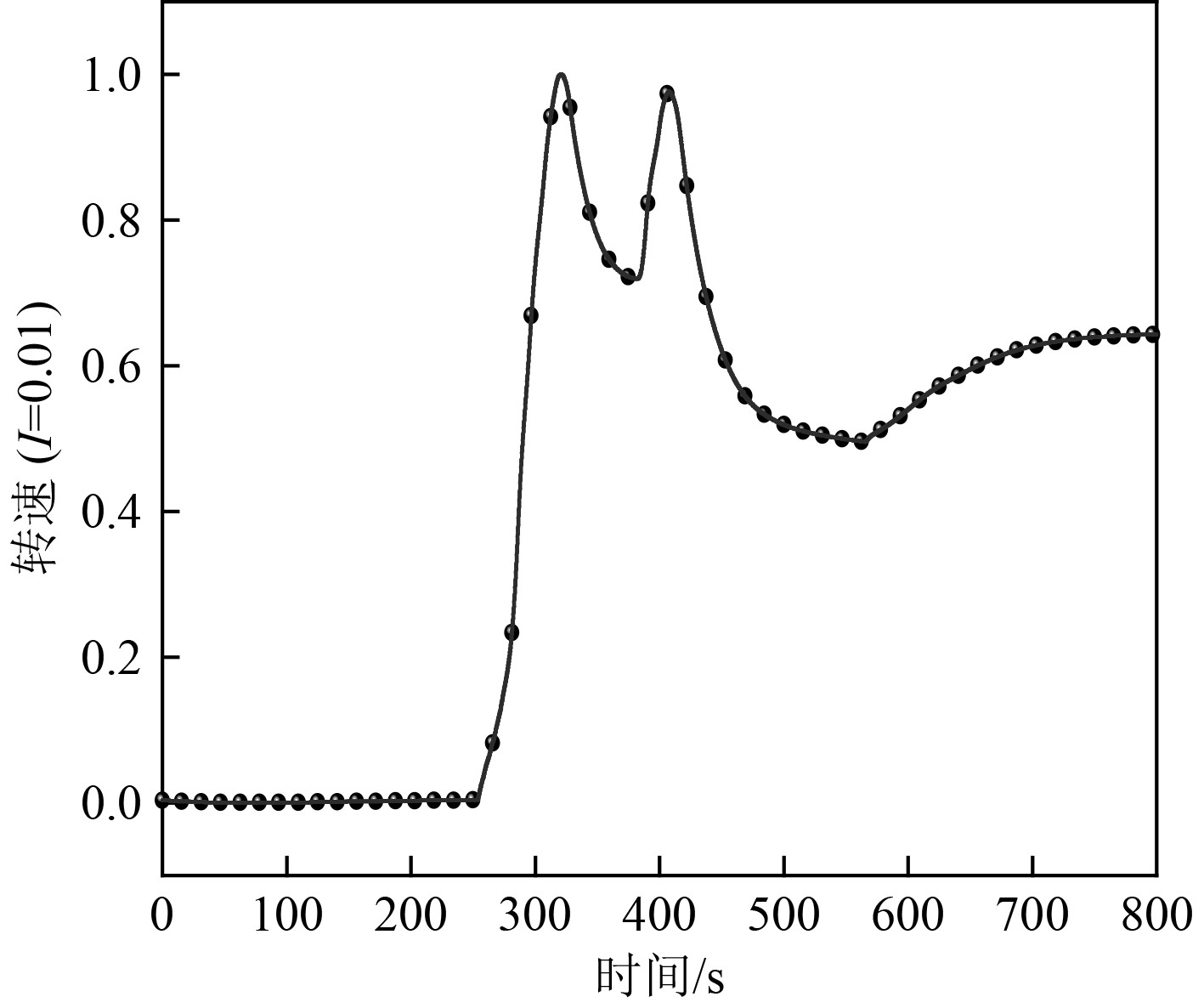
|
图 10 工况3中P=0.5、I=0.01汽轮机转速变化 Fig. 10 Working condition 3, P= 0.5, I =0.01 turbine speed change |
可知,系统在工况3状态运行时,保持比例参数为0.5不变,积分参数输入I=0.1时汽轮机转速在一个较大区间持续震荡,系统处于不稳定的状态;I=0.02时,汽轮机转速震荡幅度逐步减小;I=0.01时,系统在2次振荡之后逐步趋于稳定运行,同样具有一定自适应性。由此可见,逐渐减小积分参数输入值,系统反映出的运行稳定性变化情况和工况2大致相似。将两工况横向比较来看,为达到控制效果基本一致,所采取的积分参数比例不大相同,工况3应采用比工况2更小的积分调节参数,由此可分析得出:为保持变工况下的汽轮机转速控制稳定性,不同工况运行时应采取不同积分控制参数,工况越高应采取更小的积分调节参数。
4 结 语本文利用浮动式核电站-汽水循环系统的仿真模型复现了试验过程中出现的问题,总结出不同控制调节参数对汽轮机转速调控稳定性影响的规律,并提出相应措施,解决了试验出现的问题,归纳总结得到以下结论:
1)比例参数不变的条件下,仅改变积分参数对强耦合系统下汽轮机转速控制的效果基本不产生影响。
2)不同工况下,在比例调节参数P不变的情况下,积分调节参数I的输入值在一定范围内越小,系统运行稳定性越好。
3)在装置变工况运行条件下,不同工况汽轮机转速控制积分调节参数存在一定比例关系,升工况运行时积分调节参数应采取更小的积分调节参数。
以上分析结论在试验装置上进行了验证,结果显示上述结论合理有效。
| [1] |
张杨伟, 蔡琦, 蔡章生. 船用核动力二回路热力系统动态仿真[J]. 原子能科学技术, 2008, 42(S1): 177-181. ZHANG Yangwei, CAI Qi, CAI Zhangsheng. Dynamic simulation of marine nuclear power secondary circuit thermal system[J]. Atomic Energy Science and Technology, 2008, 42(S1): 177-181. |
| [2] |
DULAU M, BICA D. Simulation of speed steam turbine control system[J]. Procedia Technology, 2014, 12: 716-722. DOI:10.1016/j.protcy.2013.12.554 |
| [3] |
王元慧, 顾娇娇, 张晓云, 等. 船用核汽轮机转速串级前馈-反馈模糊PID控制[J]. 船舶工程, 2014, 36(1): 66-70. WANG Yuanhui, GU Jiaojiao, ZHANG Xiaoyun, et al. Cascade feed forward feedback fuzzy PID control for speed of marine nuclear steam turbines[J]. Ship Engineering, 2014, 36(1): 66-70. DOI:10.13788/j.cnki.cbgc.2014.0018 |
| [4] |
BOLEK W, SASIADEK J, WISNIEWSKI T. Two-valve control of a large steam turbine[J]. Control Engineering Practice, 2002, 10(4): 365-377. DOI:10.1016/S0967-0661(01)00153-8 |
| [5] |
孙建华, 汪伟, 余海燕. 基于模糊-PID的主机转速控制系统[J]. 工业控制与应用, 2008, 27(1): 27-29+33. |
| [6] |
苏杰, 夏国庆, 张伟. 核动力装置蒸汽轮机的广义预测自校正控制仿真研究[J]. 核科学与工程, 2007(1): 15-19. SU Jie, XIA Guoqing, ZHANG Wei. Simulation study on generalized predictive self-tuning control of steam turbines in nuclear power plants[J]. Nuclear Science and Engineering, 2007(1): 15-19. DOI:10.3321/j.issn:0258-0918.2007.01.004 |
| [7] |
雷世雄. 汽轮机转速模糊控制系统[J]. 船舶电子工程, 2009, 29: 48-49+61. LEI Shixiong. Fuzzy control system for turbine speed[J]. Naval Electronic Engineering, 2009, 29: 48-49+61. |
| [8] |
GSE. SimExec User Guide. GSE Power System, Inc. 2005.
|
| [9] |
房桐毅, 冯永明, 赵冬栾, 等. 基于 GSE仿真平台涡轮增压机组稳态研究[J]. 燃气轮机技术, 2012, 25(1): 33-37+51. FANG Tongyi, FENG Yongming, ZHAO Dongluan, et al. Research on steady state of turbocharger unit based on GSE simulation platform[J]. Gas Turbine Technology, 2012, 25(1): 33-37+51. DOI:10.3969/j.issn.1009-2889.2012.01.007 |
| [10] |
武晓航. 核电站主蒸汽系统建模与仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
 2023, Vol. 45
2023, Vol. 45
