在危及船舶安全的各类事故中,其中由海水管路破损引发的舱室大量进水最为严重[1]。通过高压空气排出水舱内的海水是船舶动力抗沉的重要操纵手段,但由于高压空气系统内的设备和附件繁杂,在实验室条件下搭建1:1的试验台架十分困难,因此常需要采用数学建模与仿真实验的研究方法开展这方面的工作[2]。作为海洋航行的重要工具,船舶技术性能的高低决定了航行的安全,而船舶抗沉技术作为关键技术之一,决定着船舶的生命力,因此,把诸多复杂条件和工况组合起来进行吹除仿真实验是十分迫切而且必要的。
高压空气系统管路设计计算的关键是管道压力以及流量的计算,因此明确高压空气系统管路内的流动状态十分关键。在水舱吹除整个管网系统建模方面:达格林等[3]分析了高压空气放空质量流量的计算方法,目前国内大多采用此方法进行相关计算。谢安恒等[4-5]通过气体热力学以及动力学理论,研究了高压空气管路内的流动状态,建立了高压空气管路的压力分布模型,并通过试验进行分析和验证,为高压空气系统管路的设计和计算提供了一定参考。徐文灿[6]和王晓东等[7]分别采用“摩擦管流理论”和“当量长度法”计算出了管道的质量流量。景东风等[8]通过理论分析、仿真计算和试验验证,对目前所采用的高压空气放空质量流量计算方法进行评估。在水舱高压吹除建模方面,叶剑平等[2]把被吹除的所有水舱看成一个大的水舱,以此建立了供气吹除水舱的简化物理模型。李其修等[9]使用VOF(volume of fraction)界面追踪多相流的方法对于单个水舱的高压吹除模型进行三维流体仿真,建立了高压空气吹除水舱数学模型。
上述研究从多个方面对管网系统和吹除模型进行了模拟仿真,对船舶安全性设计有很好的借鉴意义,但是仍存在一些不足。如在管网系统建模方面,采用传统的方法建模过程复杂、效率较低,而且精确度不高;在水舱高压吹除建模方面,传统的仿真工作均只计算了船舶的一个水舱,而且将吹除速率假定为恒值,这些假设在一定程度上降低了结果的可信度。而且整个高压空气吹除系统存在一定的复杂性,在运行过程中各个部分之间也难以避免会产生相互影响。传统的仿真工作都只将系统中的管网系统或水舱为仿真对象,利用某软件进行单独仿真,这样势必会产生误差。本文在耦合平台MPCCI下,将一维建模软件Flowmaster与三维建模软件Fluent进行联合的耦合仿真分析,对全部3个水舱进行仿真计算,并且实时更新吹除速率得出其动态特性,由此得出的结果更为可信。
1 高压空气吹除水舱数学模型选取通用多相流模型中的VOF湍流模型作为主要模型进行数值模拟,VOF方法是一种处理复杂自由表面的有效方法,其定义
水-气两相流模型中的标准
| $ \frac{\partial }{\partial t}(\rho K)+\nabla \cdot (\rho VK)=G-\rho \varepsilon +\nabla \cdot \left[(\mu +\frac{{\mu }_{T}^{}}{{\sigma }_{k}^{}})\nabla K\right],$ | (1) |
| $ \frac{\partial }{\partial t}(\rho \varepsilon )+\nabla \cdot (\rho V\varepsilon )={{\rm{C}}}_{1}^{}\frac{\varepsilon }{K}G-{{\rm{C}}}_{2}^{}\rho \frac{{\varepsilon }_{}^{2}}{K}+\nabla \cdot [(\mu +\frac{{\mu }_{T}^{}}{{\sigma }_{\varepsilon }^{}})\nabla \varepsilon ]。$ | (2) |
式中:C1和C2为定值,C1=1.44,C2=1.92;
Flowmaster是流体计算软件,适用于拓扑结构复杂的管网系统,如煤气管网、自来水管网、天然气管网等[8]。本文使用Flowmaster软件中的可压缩流模块,对高压气瓶通过系统管网向水舱放气的过程进行仿真计算,可以得到系统管网中各点的质量流量、流速、温度、压力等参数随时间变化的曲线。
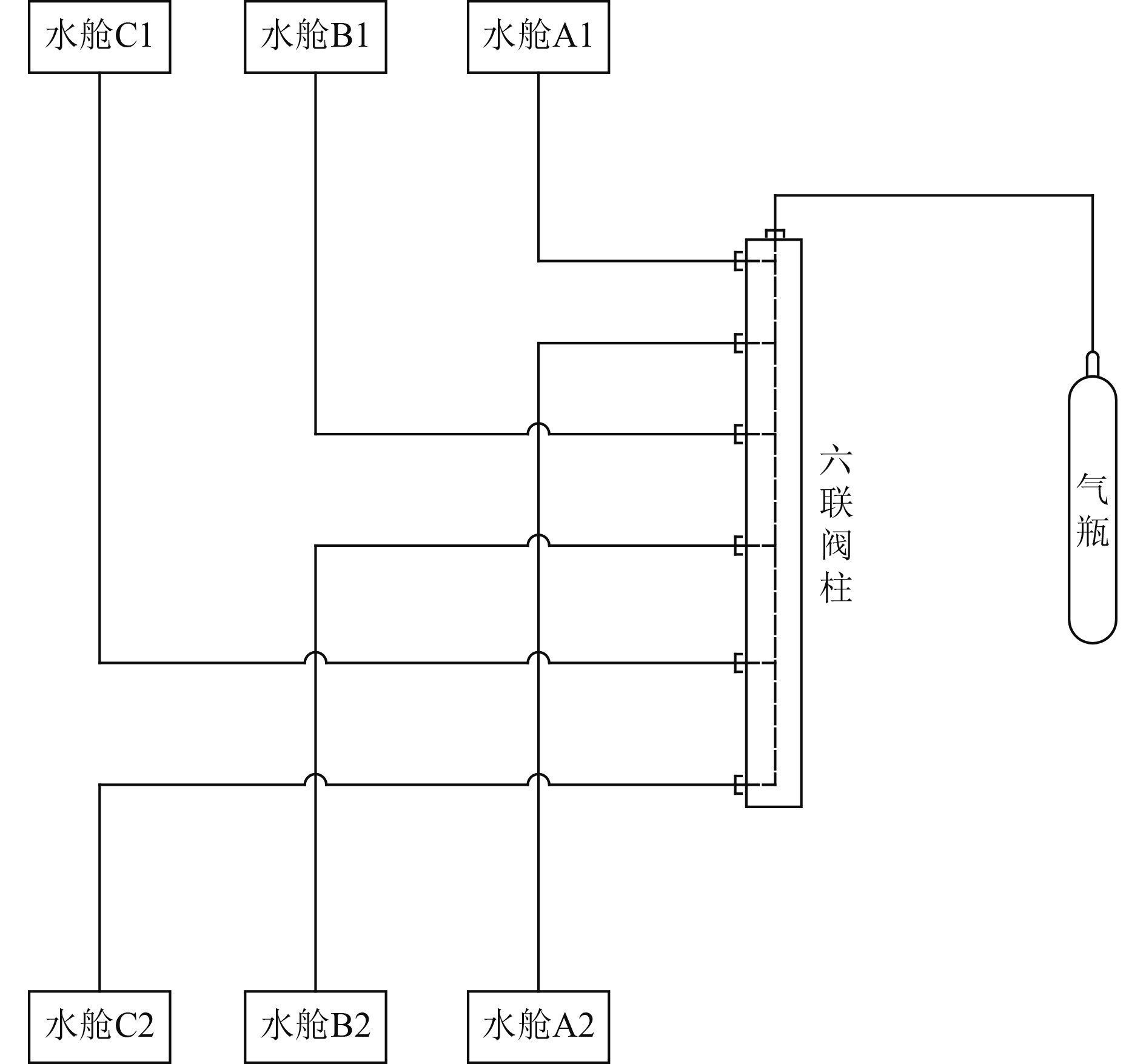
图1为Flowmaster一维管网模型,从左至右分别为3组水舱,每组水舱上下对称。由图可知整个系统由气瓶连接管网,通过阀柱分配高压空气后在经过一系列的阀门与管网最终流入6个水舱,可以看出本工况属于正常放空的工况。各元件的关键参数如表1所示。
|
图 1 复杂管网系统 Fig. 1 Complex pipe network system |
|
|
表 1 各元件的参数配置 Tab.1 Parameter configuration of each element |
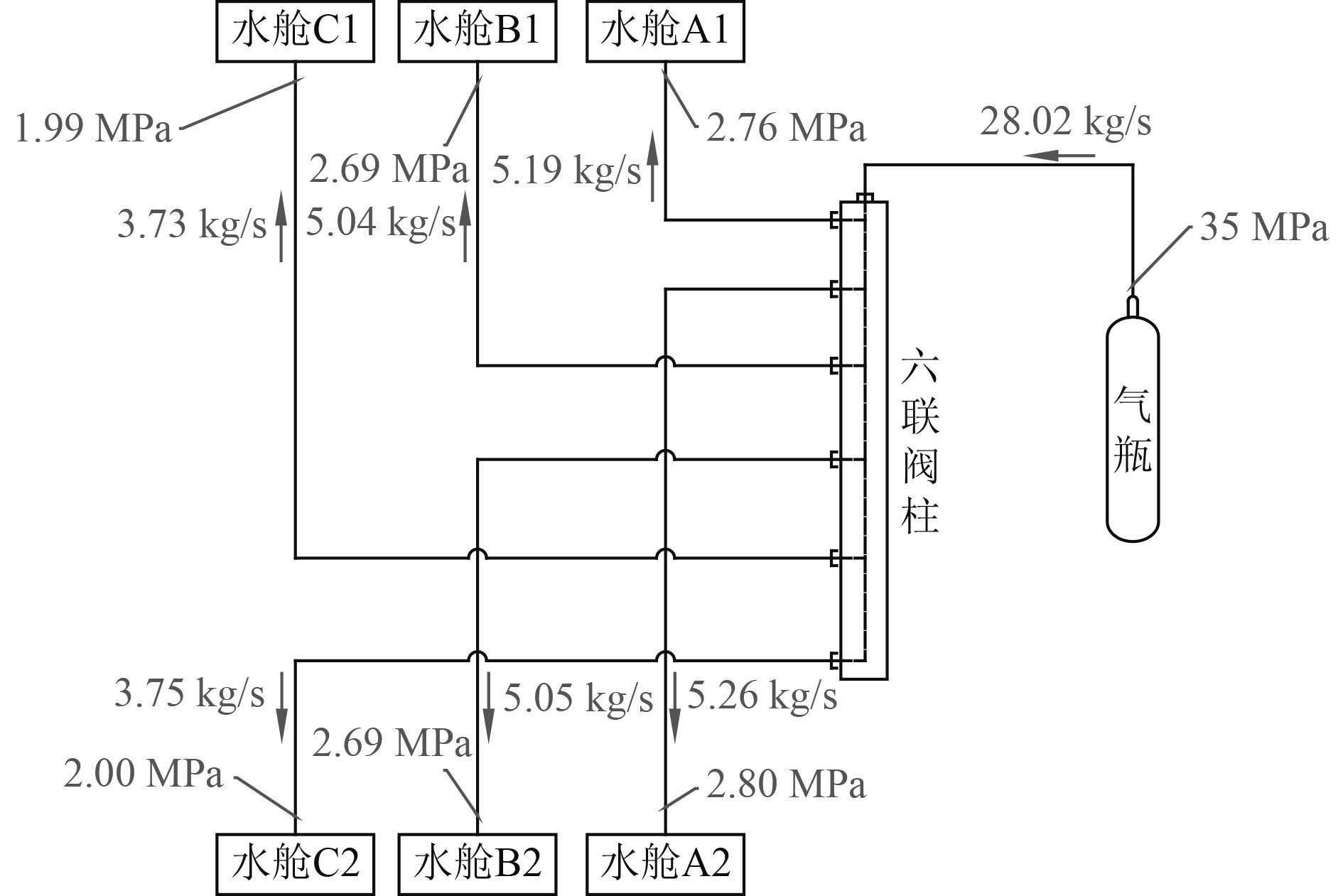
图2为一维管网动力学仿真得到的管网整体压力及流量分布结果,在气瓶出口处接有一段长度300 mm通径20 mm的管道,限制了气瓶出口的最大质量流量。管路中依然没有任何升压元件,所以压力值自气瓶到水舱单调下降。流量分配出现在DN75的六联阀柱处,由于六联阀柱下游的条件基本相同,所以每个水舱分配到的流量十分接近。6个水舱可以分为3组,每组的上下2个水舱分得的压力与质量流量基本相同,所以其排水速率也完全相同,A、B、C组单个水舱依次分得5.2 kg/s、5.0 kg/s、3.8 kg/s的质量流量,气瓶出口质量流量等于各个水舱分得的质量流量之和,约为28.02 kg/s,满足质量守恒定律且数值在合理范围内。压力方面,A、B、C组单个水舱依次分得2.8 MPa、2.7 MPa、2.0 MPa左右,水舱体积接近,水舱分得的入口压力与质量流量也接近,所以正常放空时各个水舱的协同性非常好。
|
图 2 一维仿真结果:关键点压力及流量分布 Fig. 2 One-dimensional simulation results: pressure and flow distribution at key points |
图3为3组水舱的排水过程曲线。在前述基础上对管网进行瞬态仿真分析,考察3组水舱的吹水速率。由图可知,3组水舱由于入口压力及质量流量基本相同,几何尺寸也比较接近,所以排水规律一致,中组的2个B水舱率先排完舱内载水,耗时25 s,其他2组也几乎排完,剩余载水不到10%,各舱的协同性较好,如果要达到完全同时一致排光载水的目的,可在阀柱下游对各个水舱前的管长或阀门开度进行微调。

|
图 3 一维仿真结果:3组水舱的排水过程曲线 Fig. 3 One-dimensional simulation results: drainage process curves of three tanks |
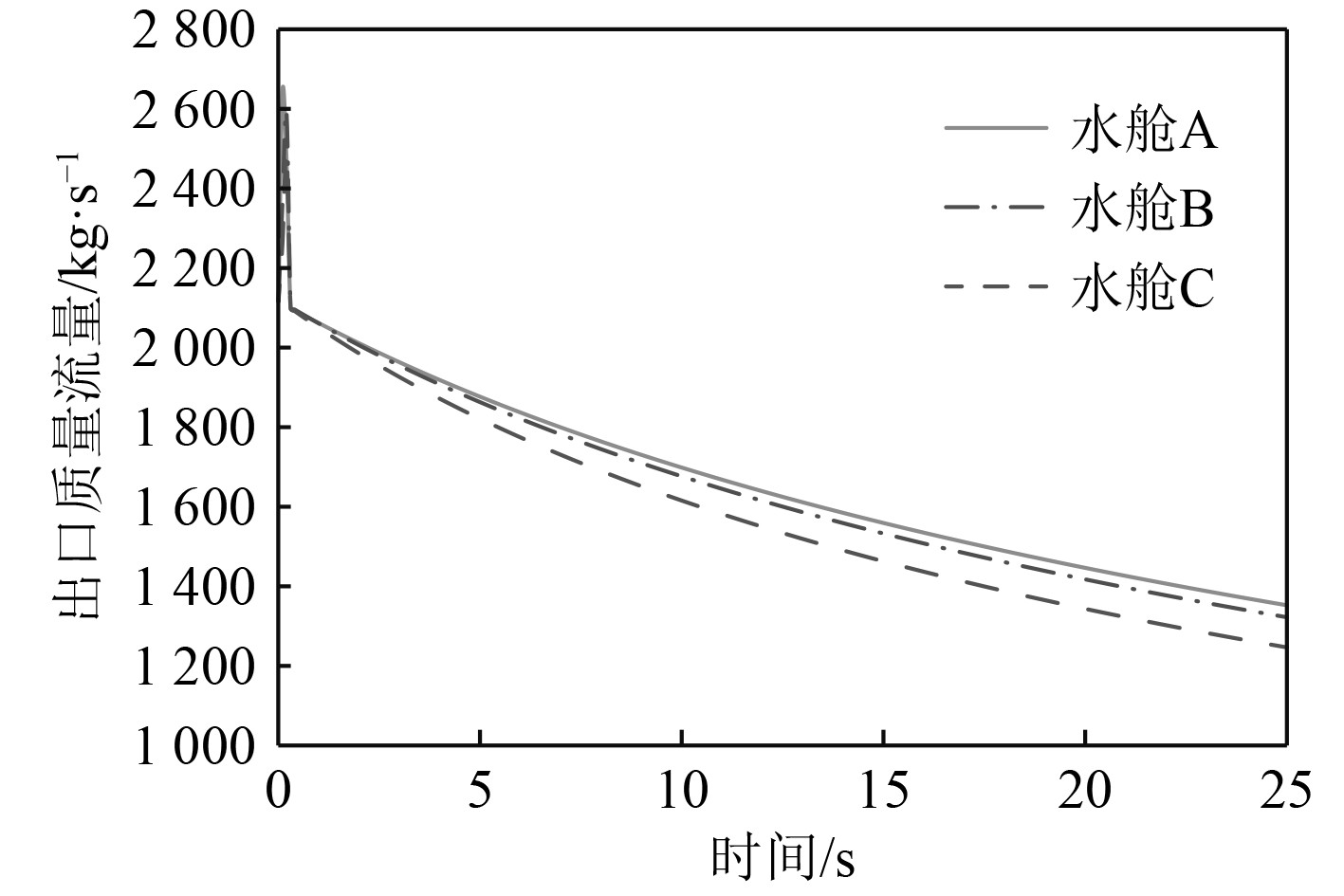
图4为各水舱的排水规律曲线,3组水舱的排水规律十分接近。排水速率在初始时刻均出现了一定程度的波动,峰值在2600 kg/s左右,然后趋于平缓,排水速率稳定下降,这是由于高压空气瓶内的压力衰减造成的结果。吹水初始阶段应是排水安全性的重要考察范围,而后面的排水过程在不受外界干扰的情况下是相对平稳和安全的。
|
图 4 一维仿真结果:水舱排水速率监测结果 Fig. 4 One-dimensional simulation results: monitoring results of tank drainage rate |
MpCCI平台是多物理场耦合的工具,可对流固耦合、流固耦合换热等重点问题进行处理,其仿真设置如图5所示。在机翼气动弹性分析、飞行器和弹体气动弹性分析、压气机和涡轮叶片气动弹性分析等问题中都有应用。本文使用MpCCI作为耦合平台,Flowmaster与Ansys-Fluent联立起来,将水舱A1、水舱B1和水舱B2的入口设定为耦合边界,仿真类型为可压缩瞬态(Compressable Transient)对该边界处的压力与质量流量2个物理量进行耦合求解。以期最终能够得到经过管网整体流场修正过的水舱流场结果。

|
图 5 耦合原理及数据类型MpCCI仿真设置 Fig. 5 Coupling principle and data type setting of MpCCI simulation |
建立水舱三维模型,右边和左边各有3个,水舱的截面积均呈月牙形且面积相等,不同体积的水舱只是长度不同。各水舱侧截面相同,仅长度不同,入口直径32 mm与水舱其他方面的几何尺寸不在一个数量级上,这不仅给流体区域的有限元网格划分增加了难度,从很大程度上增加了网格数目,降低了网格质量;而且使得入口处的马赫数和压力梯度极大,这都是不利于仿真计算的因素,会造成计算资源消耗大和计算时间长等问题。通过Gambit软件对该三维模型进行网格划分,全部采用六面体结构化网格,共计1137918个网格节点,1044151个网格单元。
3.3 合理性假设及数学模型选取在Fluent中,选取通用多相流模型中的VOF湍流模型进行仿真计算,具体模型为三维标准气液两相K-ɛ湍流模型。模型计算区域主要包含入口边界、出口边界以及Wall边界。水舱的通气阀为入口边界,水舱通海阀为出口边界,水舱的其他区域为Wall 边界。模拟初始状态时,水舱中气占单元的体积分数αG=0,水占单元的体积分数αW=1。由于水舱中的非定常表面流,水舱中的流场速度高、变化快,同时由于描述自由表面的需要,因此采用结构化网格进行划分。离散方程组采用欠松弛迭代方法求解,压力采用Body Force Weighted算法求解,压力和速度的耦合采用PISO算法求解。
3.4 数值仿真与结果对比在吹除初始阶段中,随着高压气流进入水舱,由于气体不断膨胀,此时水舱无法在短时间内排出,高压空气和水舱内的水混合在一起,在气液交界面上形成了气液混合层,在高压气入口处形成圆锥形分界面,其中气液混合层是分界面,高压气层位于分界面内部,液体层位于分界面外部。对较为危险的吹除初期进行仿真计算。
由图6和图7可知,在排水过程的初始阶段,气液两相尚未完全分离,气相和液相的激烈交汇产生了较厚的交汇层。以水舱入口的管道直径为参考,交汇层在30~80 mm,含液率约为50%。

|
图 6 0.5 s气液相云图 Fig. 6 0.5 s gas liquid phase nephogram |

|
图 7 1.0 s气液相云图 Fig. 7 1.0 s gas liquid phase nephogram |
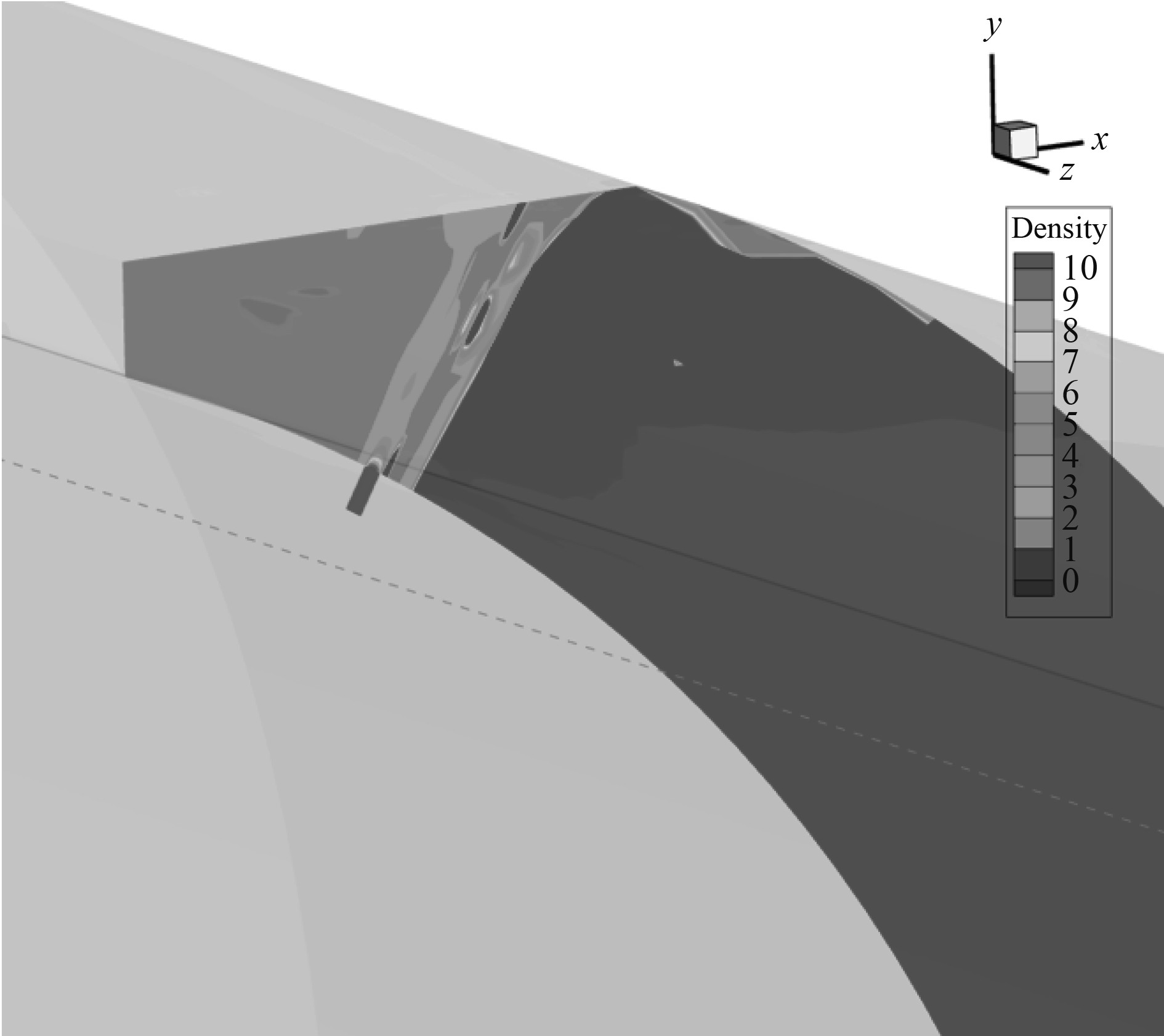
由图8可知,在进入水舱后,高压空气的被压缩程度急剧减低,入口管处的空气密度出现了阶梯状下降的趋势,入口管内原始的空气密度约在18~20 kg/m3范围内,进入水舱后经过膨胀与扩散,逐步下降到1.74 kg/m3左右,比标准大气压下空气密度(1.29 kg/m3)高出35%。
|
图 8 1.0 s密度云图 Fig. 8 1.0 s density nephogram |
由图9可知,由于空气进入密度迅速减小,入口区域内发生了膨胀吸热效应,使得周围温度迅速降低,温度变化较大的区域与密度变化较大的区域基本保持一致,在入口速度最大处也是温度最低处,最低局部温度甚至达到了140 K(−133°C)。

|
图 9 1.0 s温度云图 Fig. 9 1.0 s temperature nephogram |
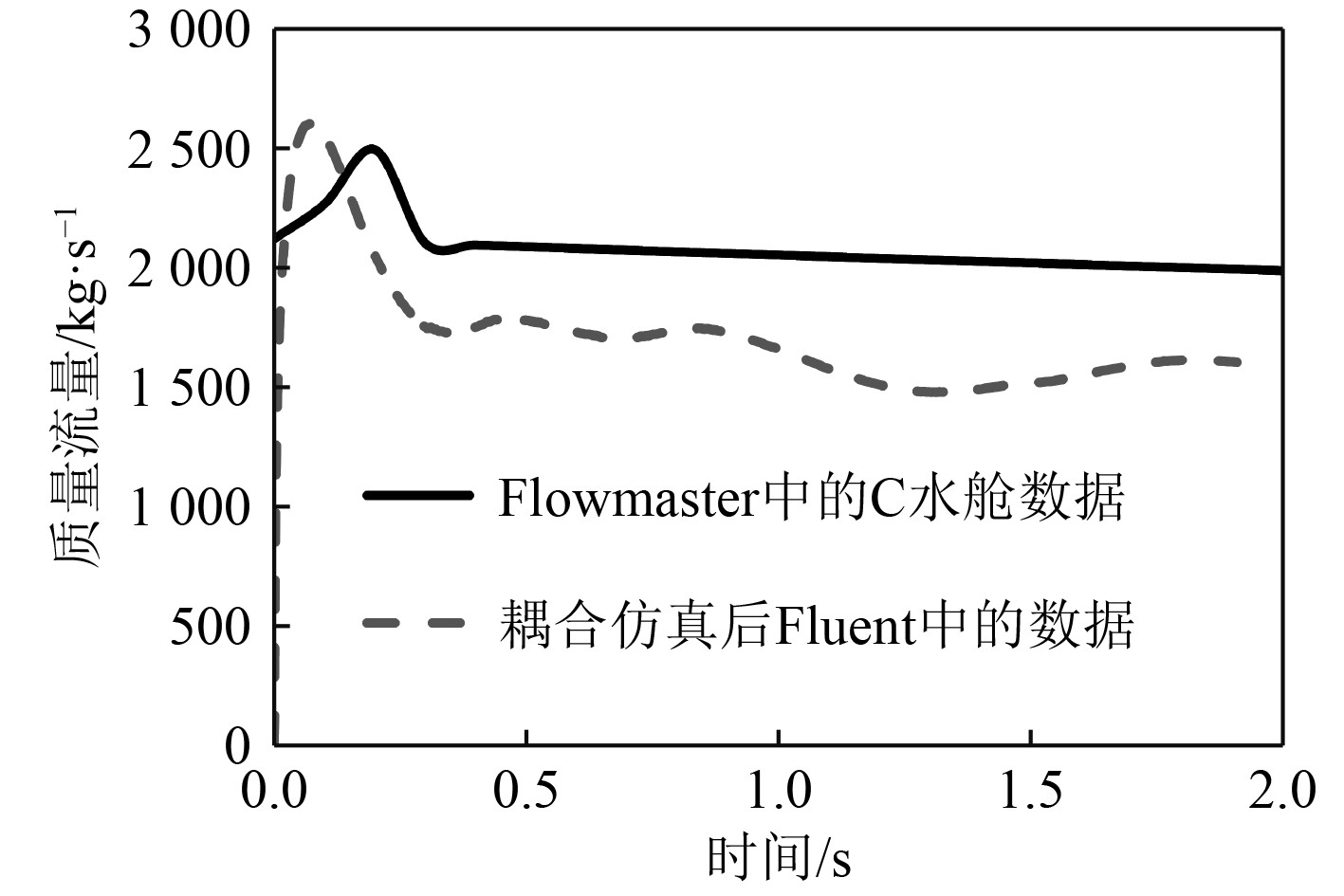
此外,为了分析一维仿真结果与一维三维耦合仿真结果的差异性,图10为水舱C出口质量流量的对比,可知在前2 s内2种仿真手段得到的水舱出口排水速率曲线有着较高的一致性和吻合性,流量峰值都在2500 kg/s左右,稳定值都在1900 kg/s左右。这一结果表明,Flowmaster一维流体仿真虽然不能计算水舱内的压力等参数,但是在计算出口质量流量时准确性较高。
|
图 10 C舱排水速率一维与三维仿真结果对比 Fig. 10 Comparison of one-dimensional and three-dimensional simulation results of C tank drainage rate |
本文以高压空气系统管网整体的动力特性和水舱的安全性为研究对象,分3种不同情况进行仿真分析,并对建立的模型进行仿真计算,为下一步进行高压空气吹除水舱台架实验提供理论基础,得出以下结论:
1)针对具体实际的吹除工况,运用一维Flowmaster流体软件对管网动力特性进行研究,得到了各个关键节点的关键数据。同时,通过对3舱同时吹除的仿真分析,得到了吹除水舱所需要的准确时间与质量流量变化曲线。
2)基于MpCCI的一维与三维耦合仿真技术,使用Fluent软件中的VOF界面追踪多相流方法对于多个水舱的高压吹除模型进行了三维流体仿真。通过MpCCI平台实现了Flowmaster和Flunet的数据对接,实现了对三维多水舱模型内的温度、密度、速度等结果进行求解,同时得到了输入为动态变化量时水舱出口流量变化结果以及吹除水舱所需时间,以动态输入、多舱同时吹除的仿真分析更真实地模拟了实际水舱的吹除情况,为高压空气吹除的安全性提供了一定的指导和借鉴意义。
| [1] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995: 149–165.
|
| [2] |
叶剑平, 戴余良, 李亚楠. 潜艇主压载水舱高压气吹除系统数学模型[J]. 舰船科学技术, 2007, 29(2): 112-115+126. |
| [3] |
达林格J F, 麦克盖尔J E. 船舶高压空气系统的附录和探讨[Z]. 1962.
|
| [4] |
谢安恒, 高院安, 周华. 高压气体系统管道流动研究与实验分析[J]. 液压与气动, 2008(9): 67-70. DOI:10.3969/j.issn.1000-4858.2008.09.027 |
| [5] |
刘辉, 滇金云, 金涛. 潜艇高压气吹除主压载水舱系统模型研究[J]. 舰船科学技术, 2010, 32(9): 26-30. DOI:10.3404/j.issn.1672-7649.2010.09.006 |
| [6] |
徐文灿. 计算气管道的流量特性[J]. 液压与气动, 1986(4): 22-24. |
| [7] |
王晓东, 李维嘉, 谢江辉, 等. 船舶潜浮系统仿真研究初探[J]. 舰船科学技术, 2004, 26(1): 14-19. |
| [8] |
景东风, 刘潜. 船舶高压空气复杂管网放空计算与试验[J]. 舰船科学技术, 2012, 34(2): 63–69.
|
| [9] |
李其修, 刘辉, 吴向君. 基于CFD的潜艇高压气吹除主压载水舱系统模拟[J]. 舰船科学技术, 2012, 34(9): 56–60.
|
 2023, Vol. 45
2023, Vol. 45
