2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
碳纤维增强树脂(Carbon Fibre-reinforced Polymer, CFRP)复合材料由于具有较高的比强度、比模量,可设计性强以及重量较轻等优势,在船舶上层建筑中应用的越来越广泛。在实际工程结构设计中,复合材料连接接头强度设计必不可少,由于复合材料的脆性特征和材料性能的各向异性,复合材料连接结构设计比传统金属连接结构设计要复杂的多[1]。
CFRP复合材料连接结构设计的目标为在满足各种限制条件的情况下实现更高的连接强度,连接方式有机械连接、胶接、焊接、混合连接等。其中胶接具有无钻孔产生的应力集中、抗疲劳、密封性好等优点。胶接结构的强度分析方法可分为试验法、解析法和数值法等,数值法主要是有限元方法[2]。近年来,国内外研究学者基于不同的胶层失效准则和复合材料层合板失效准则,对复合材料胶接结构连接强度进行了大量的研究。郭霞等[3]研究了搭接长度对复合材料胶接接头的影响,发现不同搭接长度情况下胶接接头破坏模式不同。毛振刚等[4]研究了几种现成的铺层顺序对复合材料层合板胶接结构连接性能和损伤行为的影响。Sulu[5]研究了在拉伸载荷作用下复合材料双搭胶接结构的最优铺层角度、搭接长度和搭接宽度,得到了一组最优胶接参数。
对于复合材料胶接结构强度设计,层合板的铺层顺序设计是其中的重要一环,而铺层顺序为非线性参数,且改变铺层顺序可能会牵动复合材料自身强度,甚至出现局部连接强度提高但整体强度减弱的无效优化。前人对CFRP复合材料层合板胶接结构最优铺层顺序的研究大多局限于少数几种现成方案的优选,结果偶然性大,较少采用智能算法进行全局优化方案求解,并且少有关注铺层顺序改变对CFRP复合材料层合板本身强度的影响。本文兼顾复合材料自身强度及胶接结构连接强度,采用遗传算法对所有满足设计要求的铺层方案进行全局寻优。
遗传算法(Gentic Algorithms,GA)是一种模拟自然选择和生物进化机制的全局概率搜索算法,对一定条件约束下随机生成的初始种群进行选择、交叉、变异操作,逐步改进种群,直到搜索到最优解或达到收敛条件。近年来,遗传算法越来越多地运用到复合材料铺层优化设计当中。Park等[6]使用遗传算法优化对称复合材料层压板的设计,给出了不同边界条件和载荷下的铺层优化结果。郭琰等[7]使用遗传算法以一阶固有频率最大化为设计目标对开孔复合材料层合板铺层角度进行优化。陆振玉等[8]提出了改进的自适应遗传算法,其交叉和变异算子在迭代过程中能够根据种群迭代收敛趋势进行自适应调整,提高了复合材料铺层优化计算效率。以上研究考虑的是CFRP复合材料层合板本身的强度。
胡春幸等[9]基于遗传算法和二次多项式响应面代理模型对复合材料层合板胶接结构进行了搭接长度、搭接宽度、胶层厚度等3个参数优化。前人基于遗传算法对复合材料胶接结构的其他参数进行了较多研究,而对铺层顺序优化研究较少。
本文采用多岛遗传算法进行全局搜索,将CFRP复合材料层合板本身强度作为约束条件,进而对胶接结构强度进行双层迭代优化,并对比分析遗传算法控制参数对优化效率和优化稳定性的影响。
1 CFRP复合材料层合板胶接结构优化相关理论 1.1 CFRP复合材料层合板渐进损伤模型计算CFRP复合材料层合板失效过程时,本文采用Hashin失效准则[10],表达式如下:
纤维拉伸失效
| $ {e_{ft}} = {\left( {\frac{{{\sigma _{11}}}}{{{X_t}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} \geqslant 1,{\sigma _{11}} \geqslant 0 。$ | (1) |
纤维压缩失效
| ${e_{fc}} = {\left( {\frac{{{\sigma _{11}}}}{{{X_c}}}} \right)^2} \geqslant 1,{\sigma _{11}}<0 。$ | (2) |
基体拉伸失效
| $ \begin{aligned} {e_{{mt}}} = & \frac{{{{({\sigma _{22}} + {\sigma _{33}})}^2}}}{{{Y_t}^2}} + \frac{{\tau _{23}^2 - {\sigma _{22}}{\sigma _{33}}}}{{S_{23}^2}} + \\ & {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} \geqslant 1,({\sigma _{22}} + {\sigma _{33}}) \geqslant 0。\end{aligned} $ | (3) |
基体压缩失效
| $ \begin{split} {e_{mc}} = & \frac{1}{{{Y_c}}}({(\frac{{{Y_c}}}{{2{S_{23}}}})^2} - 1)({\sigma _{22}} + {\sigma _{33}}) + \frac{{{{({\sigma _{22}} + {\sigma _{33}})}^2}}}{{4S_{23}^2}} + \\ & \frac{{\tau _{23}^2 - {\sigma _{22}}{\sigma _{33}}}}{{S_{23}^2}} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2}1,\\ & ({\sigma _{22}} + {\sigma _{33}}) < 0。\end{split} $ | (4) |
式中:σ11、σ22、σ33为材料正应力;τ12、τ23、τ13为剪应力;XT和XC为材料的纤维方向拉伸和压缩强度;YT和YC为垂直于纤维方向的拉伸和压缩强度;S12、S13、S23为相应方向上的剪切强度。
当材料符合Hashin失效准则时,载荷继续增加会导致材料刚度系数退化,建立CFRP复合材料层合板材料损伤本构关系[4]:
| $ \sigma = {{\boldsymbol{C}}_d}\varepsilon 。$ | (5) |
式中:σ为应力;ε为应变;Cd为刚度矩阵,受连续损伤变量控制。
本文用连续损伤变量di描述复合材料损伤,下标i为ft、fc、mt、mc,分别代表纤维拉伸、纤维压缩、基体拉伸、基体压缩,di控制着刚度系数,其取值范围为[0,1]。当di=0时,表示没有损伤;当di=1时,表示结构完全失效,CFRP复合材料层合板的损伤变量公式为[10]:
| $ {d_i} = 1 - \left(\frac{1}{{{e_i}}}\right){{\text{e}}^{( - {C_{11}}\varepsilon _{11}^i\varepsilon _{11}^i({e_i} - 1){L_C}/{G_i})}} 。$ | (6) |
式中:Gft、Gfc、Gmt、Gmc为CFRP复合材料层合板4种失效形式下的断裂能;Lc为特征长度。
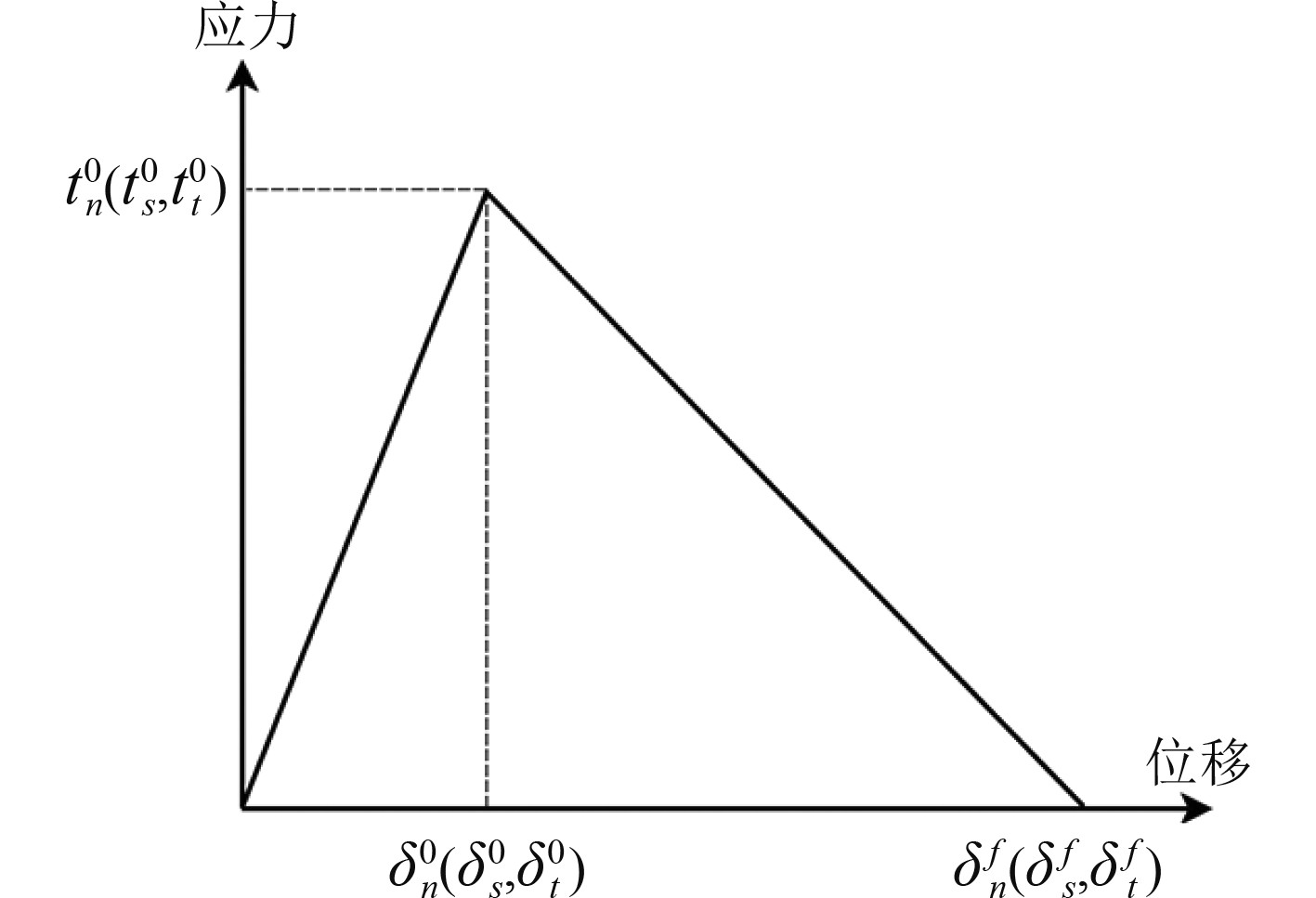
1.2 胶层渐进损伤模型计算CFRP复合材料层合板胶接接头失效过程时,用拉伸-分离准则来描述胶的力学行为,描述材料到达强度极限前的线弹性阶段和材料到达强度极限后的刚度线性降低软化阶段,如图1所示。
|
图 1 拉伸-分离准则[10] Fig. 1 Traction-Separation law |
本文采用的胶合初始损伤判断准则为二次名义应力准则[10],如下:
| $ {\left( {\frac{{{\sigma _n}}}{{t_n^0}}} \right)^2} + {\left( {\frac{{{\sigma _s}}}{{t_s^0}}} \right)^2} + {\left( {\frac{{{\sigma _t}}}{{t_t^0}}} \right)^2} = 1。$ | (7) |
式中:
| $ t = (1 - D){\rm{diag}}({K_{nn}},{K_{ss}},{K_{tt}})\delta 。$ | (8) |
式中:D为刚度折减系数,其取值范围为[0,1]。D=0时,胶层单元未损伤;D=1时,胶层单元完全失效。材料的刚度退化过程和最终失效位移由临界应变能释放率GTC控制,GTC为图1中应力-位移曲线下的面积。
胶层单元的临界应变能释放率GTC由B-K准则[11]来计算:
| $ {G}_{TC}={G}_{n}^{C}+({G}_{s}^{C}-{G}_{n}^{C}){\left(\frac{{G}_{s}}{{G}_{T}}\right)}^{\eta } 。$ | (9) |
式中:
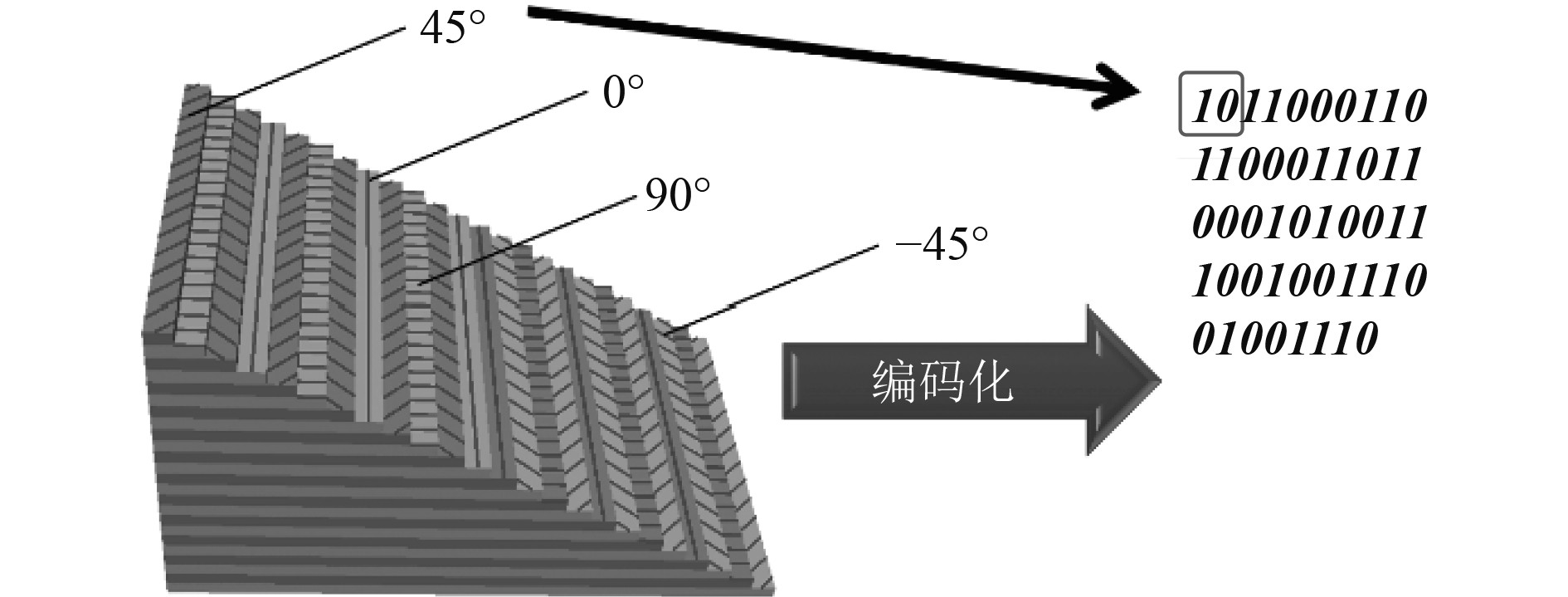
应用遗传算法首先需要解决实际物理问题向抽象数学表达的编码问题,编码的好坏很大程度影响了优化问题的求解效率及稳定性。遗传算法主要有:二进制编码、格雷码编码、实数编码、符号编码算法等,二进制编码是应用最早和最广的编码方法,具有编码和解码简单,交叉、变异等遗传操作易于实现等优点。本文选用二进制编码,将铺层角度转换为二进制,−45°、0°、45°、90°分别编码成00、01、10、11,具体如图2所示。
|
图 2 [45, 90, −45, 0]3s铺层二进制编码示意 Fig. 2 [45, 90, −45, 0]3s layup binary encoding illustration |
适应度是评判遗传算法中个体优劣的标准,遗传操作也根据适应度的大小决定个体繁殖的机会,适应度值大的个体得到繁殖的机会大于适应度值小的个体,从而使得新种群的平均适应度值高于旧群体的平均适应度值。本文采用极限失效载荷作为适应度,极限失效载荷越大,适应度越大。
由于不是所有铺层角度都是有效的,所以需要对铺层角度进行约束,本文采用罚函数法将非线性规划问题转化为无约束极值问题。罚函数法是对任一违反了约束条件的个体,把该个体的适应度值降低,从而使得该个体较难产生后代。
传统遗传算法的遗传操作一般分为选择、交叉、变异。选择是从当前的种群中选出优良的个体,使其有机会作为父代产生后代个体。交叉是将选择出来的个体作为双亲作基因链码的交叉,从而产生2 个新的个体作为其后代。变异是通过对某些位置上的基因进行改变,从而产生新的个体。
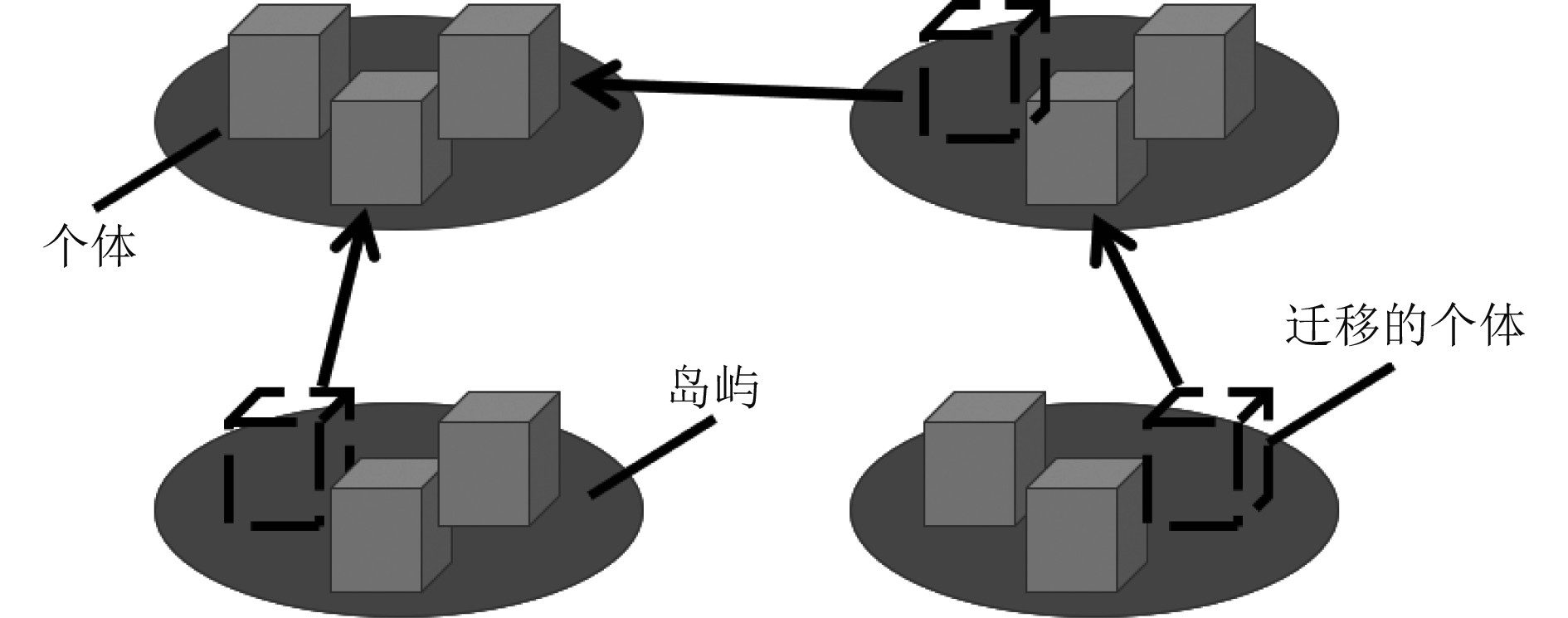
本文采用的多岛遗传算法,将初始种群分为数个子种群,子种群在平时互不干扰,子种群内仍然会发生传统遗传算法的选择、交叉、变异等操作,只有偶尔会发生迁移,交换不同子种群中的个体。该算法作为一种伪并行的算法不容易局限在设计点周围区域寻优,更容易求解全局最优值,抑制了早熟现象。
|
图 3 多岛遗传算法示意 Fig. 3 Multi-island genetic algorithms illustration |
毛振刚等[4]对CFRP复合材料层合板单搭胶接结构连接强度进行了试验研究。本文以此试验所用的试样结构及材料参数作为基础,对比验证单搭胶接结构强度数值预报模型的合理性。
采用T300/7901碳纤维增强树脂复合材料,层合板厚度为3.6 mm;搭接长度为20 mm;层合板尺寸为120 mm×25 mm×3.6 mm;铺层顺序为 [45,90,−45,0]3s。胶膜采用LJM-170型中温固化环氧树脂基胶膜,胶膜厚度0.12 mm。表1为T300/7901碳纤维增强树脂复合材料层合板的材料参数,表2为LJM-170胶膜的材料参数。
|
|
表 1 T300/7901CFRP复合材料层合板材料参数[4] Tab.1 T300/7901CFRP Composite Laminate Material Parameters |
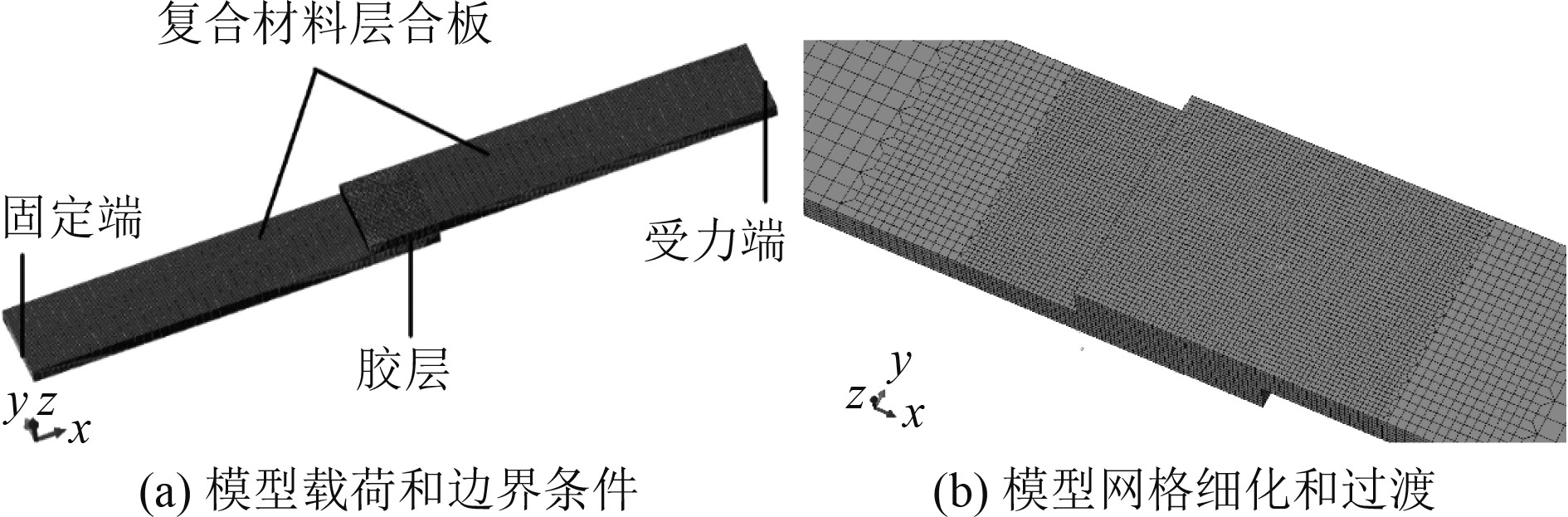
基于上述材料参数和损伤模型,使用有限元分析软件建立单搭胶接结构,为节约计算成本,仅细化搭接区及周边部分网格,边缘区域进行过渡。模型的载荷、边界条件如图4所示,即模型的左端为刚性固定约束,在受力端施加搭接方向的拉伸载荷,求解连接接头极限强度。
|
|
表 2 LJM-170胶膜的材料参数[4] Tab.2 LJM-170 adhesive film material parameters |
|
图 4 CFRP复合材料层合板单搭胶接结构 Fig. 4 CFRP composite laminate single-stack bonded structure |
将搭接长度L=20 mm的CFRP复合材料层合板单搭胶接结构的载荷-位移曲线预报结果与文献[4]的试验结果进行对比(见图5),仿真结果与试验结果变化趋势基本一致。随着拉伸载荷增加,结构受载以直线状态逐渐增大,结构达到极限承载能力时,胶层及附近的复合材料层合板发生损伤失效,结构承载能力随之下降,仿真结果的最大失效载荷比试验值略大一些,最大误差为6.4%。可见,本文数值模型能比较准确地预报CFRP复合材料层合板单搭胶接结构在拉伸载荷作用下的承载能力,可用于后续的计算分析。
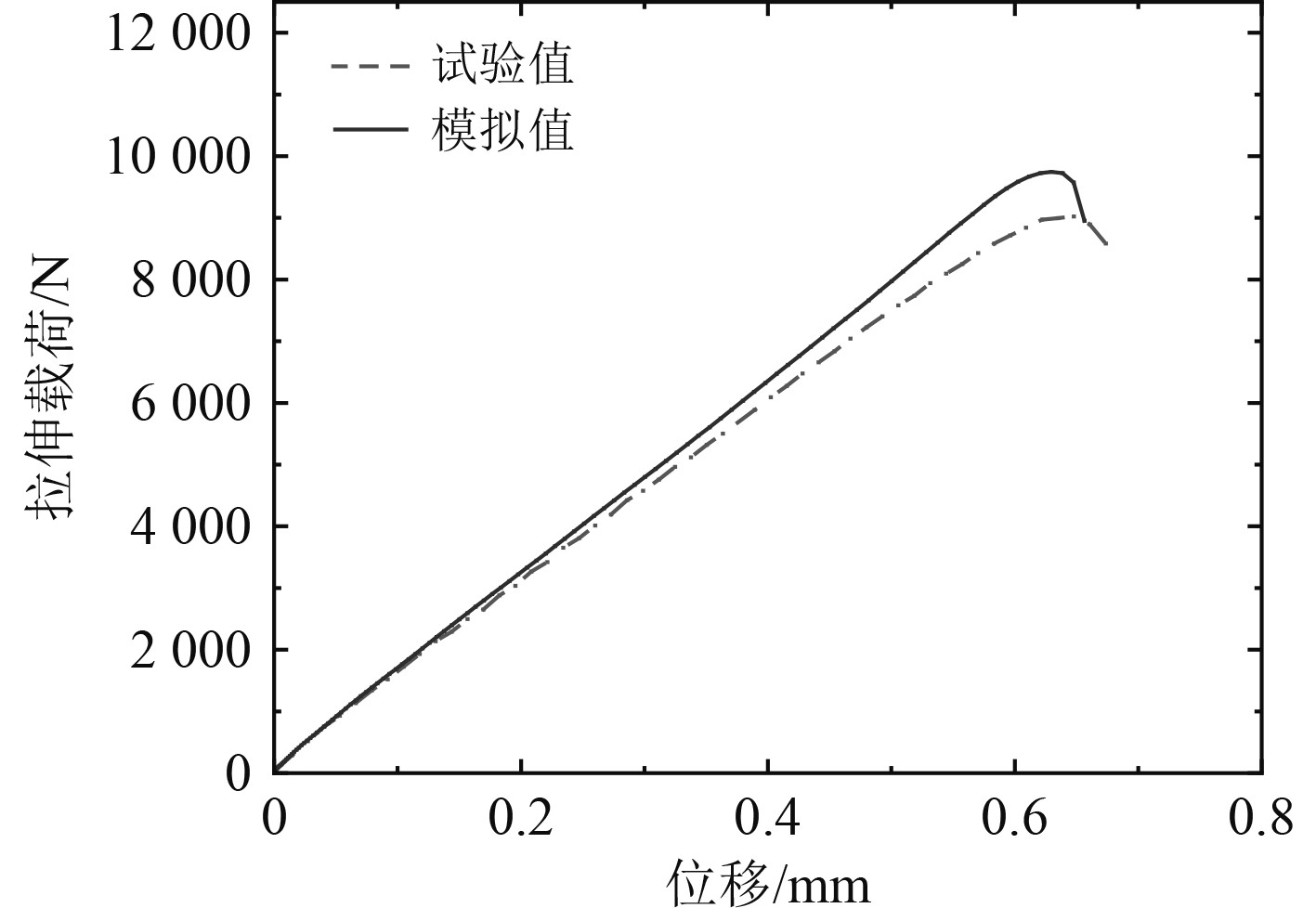
|
图 5 CFRP复合材料层合板单搭胶接结构拉伸载荷-位移曲线 Fig. 5 CFRP composite laminate single-stack bonded structure Tensile load-displacement curve |
复合材料可以通过改变铺层方式在一定范围内改变其性能以满足不同要求。CFRP复合材料层合板的铺层方式优化问题是一个离散的叠层顺序优化问题,可能存在多个极值点,求解起来较为困难,可采用遗传算法等人工智能算法进行优化。将《复合材料结构设计手册》中的复合材料层合板铺层顺序约束条件数学化,并将CFRP复合材料层合板的拉伸强度作为优化目标。
优化问题:寻找最优铺层角度[θ1, θ2, θ3, θ4, θ5, θ6, θ7, θ8, θ9, θ10, θ11, θ12]s。
目标函数:MAX_Fs为复合材料层合板拉伸方向极限失效载荷最大。
收敛判断:连续5 代种群里每一代中较大的5个极限失效载荷的平均值Fs变化小于1%为收敛。
约束条件[13]:
1)
2)θi∈ (−45°, 0°, 45°, 90°),pθ=−45° ≥ 6,pθ=0° ≥ 6,pθ=45° ≥ 6,pθ=90° ≥ 2,p为铺层数量;
3)
4)
通过前期试算发现,本文的优化问题是一个较快收敛的问题。综合考虑收敛效率和遗传算法的稳定性,取较少的岛数、较小的交叉概率和较小的变异概率,各参数值设置如表3所示。
|
|
表 3 拉伸强度优化参数设置 Tab.3 Tensile strength optimization parameter settings |
通过多岛遗传算法优化计算,得到结果如图6所示。
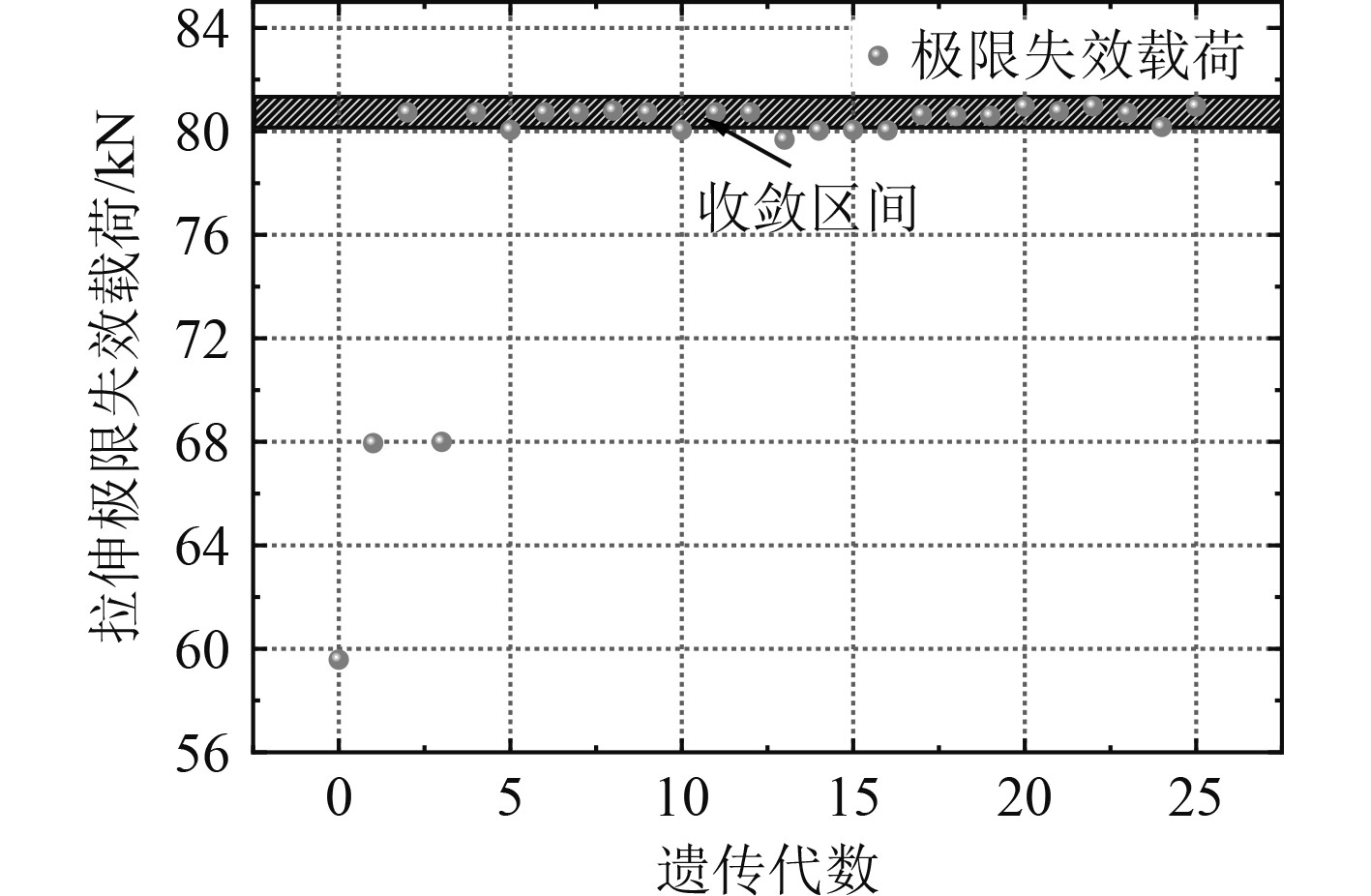
|
图 6 复合材料层合板拉伸强度优化结果 Fig. 6 Composite laminate tensile strength optimization results |
在铺层顺序满足约束条件时,拉伸极限失效载荷最大为80985 N,考虑到对复合材料胶接结构进行优化时,不应大幅度改变复合材料层合板本身的拉伸强度,故将复合材料层合板的拉伸极限失效载荷不小于最大值的80%作为额外约束条件。
4 胶接结构连接强度的铺层方式双层优化设计 4.1 胶接结构拉伸强度及剥离强度相关性验证在实际工程运用中,CFRP复合材料层合板胶接结构主要受到面内拉伸及面外剥离2 种载荷形式。采用蒙特卡罗法在满足铺层方式约束条件的情况下,对CFRP复合材料层合板铺层角度参数进行25次随机采样,计算不同铺层参数下的CFRP复合材料层合板胶接结构的拉伸极限失效载荷和剥离极限失效载荷,结果如图7所示。拉伸载荷和剥离载荷作用下的铺层结构应力图如图8和图9所示。

|
图 7 剥离-拉伸极限失效载荷关系图 Fig. 7 Peel-stretch limit failure load diagram |

|
图 8 拉伸载荷作用下铺层胶接结构应力图 Fig. 8 Stress diagram of the laminated bonding structure under tensile load |

|
图 9 剥离载荷作用下铺层胶接结构应力图 Fig. 9 Stress diagram of the laminated bonding structure under peeling load |
可知,在本文的胶膜参数和CFRP复合材料层合板参数下,CFRP复合材料层合板胶接结构的剥离极限失效载荷与拉伸极限失效载荷成正比,这是因为无论在拉伸载荷、还是在剥离载荷的作用下,胶接方向应力占主要部分,即纤维0°方向的铺层都起到主导作用,故在后文双层优化中,只对CFRP复合材料层合板的最大拉伸强度和胶接结构的面内拉伸强度进行双层迭代优化。
4.2 双层优化流程及参数设计胶接结构连接强度只是CFRP复合材料层合板强度设计中考虑的一部分,所以在通过改变CFRP复合材料层合板的铺层方式从而改变胶接结构连接强度时,不应大幅度改变CFRP复合材料层合板本身的强度。
故本文采用双层优化,先对CFRP复合材料层合板的拉伸强度进行关于铺层方式的优化,将得到的优化结果作为限制条件,再对CFRP复合材料层合板胶接结构面内拉伸强度进行关于铺层方式的优化。
优化问题:寻找最优铺层角度[θ1, θ2, θ3, θ4, θ5, θ6, θ7, θ8, θ9, θ10, θ11, θ12]s。
目标函数:MAX_Fd为单搭胶接结构拉伸极限失效载荷最大。
收敛判断:连续5 代种群里每一代中较大的5个极限失效载荷的平均值Fd变化小于1%为收敛。
约束条件[13]:
1)
2)
3)
4)
5)
流程如图10所示。
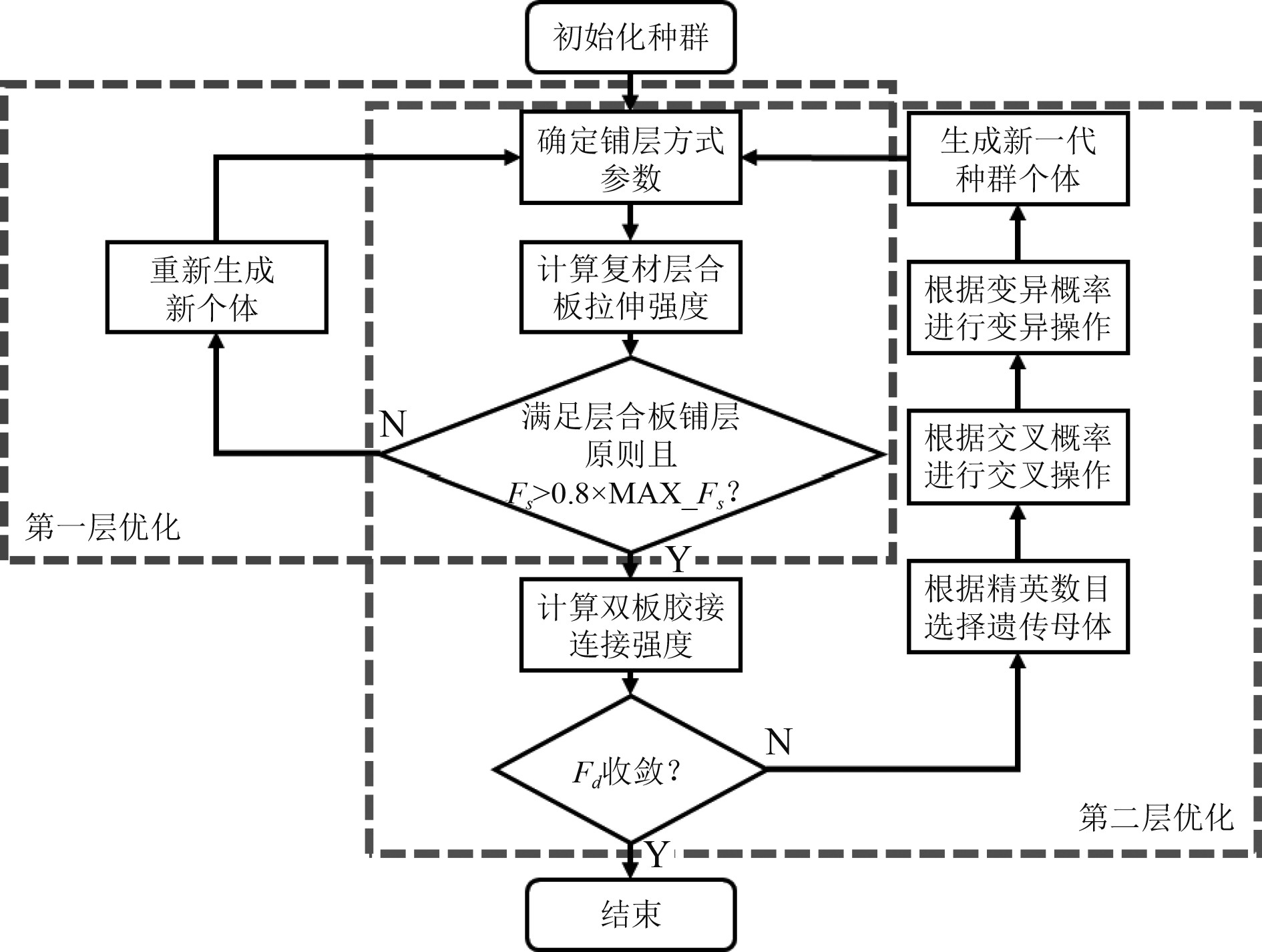
|
图 10 双层优化流程图 Fig. 10 Two-tier optimization flowchart |
沿用表3的遗传算法控制参数进行双层优化,经过一系列的迭代计算之后得到了极限失效载荷和遗传代数的收敛关系,如图11所示。

|
图 11 胶接结构拉伸强度优化结果 Fig. 11 Optimization results of tensile strength of glued structures |
将优化前后的CFRP复合材料层合板胶接结构的拉伸极限失效载荷进行对比,如图12和表4所示。
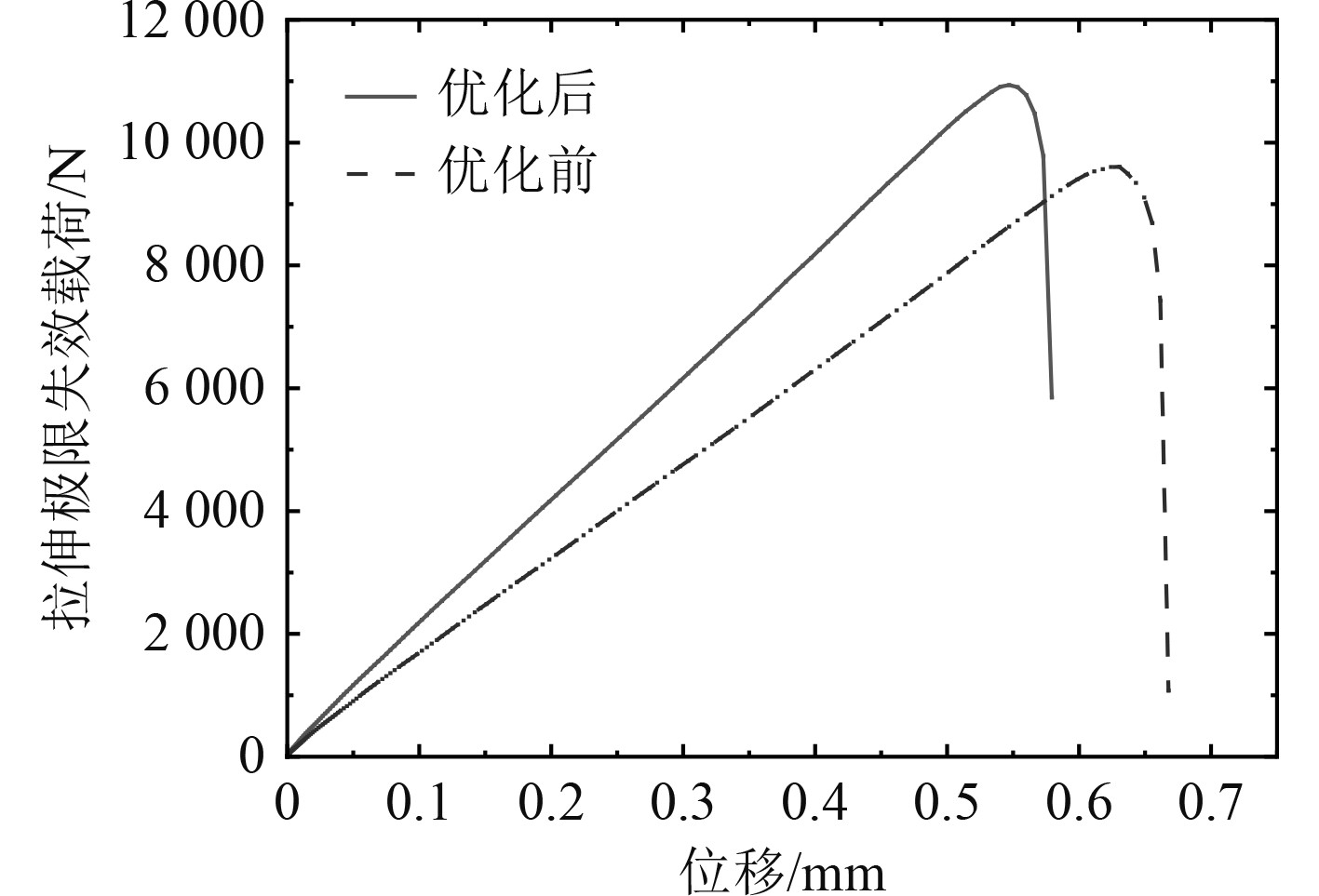
|
图 12 优化前后拉伸极限失效载荷-位移曲线对比 Fig. 12 Tensile limit failure load-displacement curve comparison |
|
|
表 4 优化前后结果对比 Tab.4 Compare results before and after optimization |

|
图 13 胶层剪切失效 Fig. 13 Layer shear failure |
|
|
表 5 前五优化结果对比 Tab.5 Comparison of the top 5 optimization results |
可以发现,复合材料铺层纤维方向为
多岛遗传算法中各参数如岛数、交叉概率、变异概率等均会影响优化效率和稳定性,所以需对遗传算法控制参数的铺层优化影响进行研究。
5.1 岛数影响效应多岛遗传算法中,每一代的总群体个数为岛数乘以每个岛的群体个数。一般而言,在总群体个数不变的情况下,岛数越少,越快收敛,但越容易出现局部收敛,所以应在保证全局收敛的条件下,减少岛数。
将总群体个数取为20个,根据表3的遗传算法参数设置,在其他参数不变的情况下,将岛数改变,得到结果如图14所示。
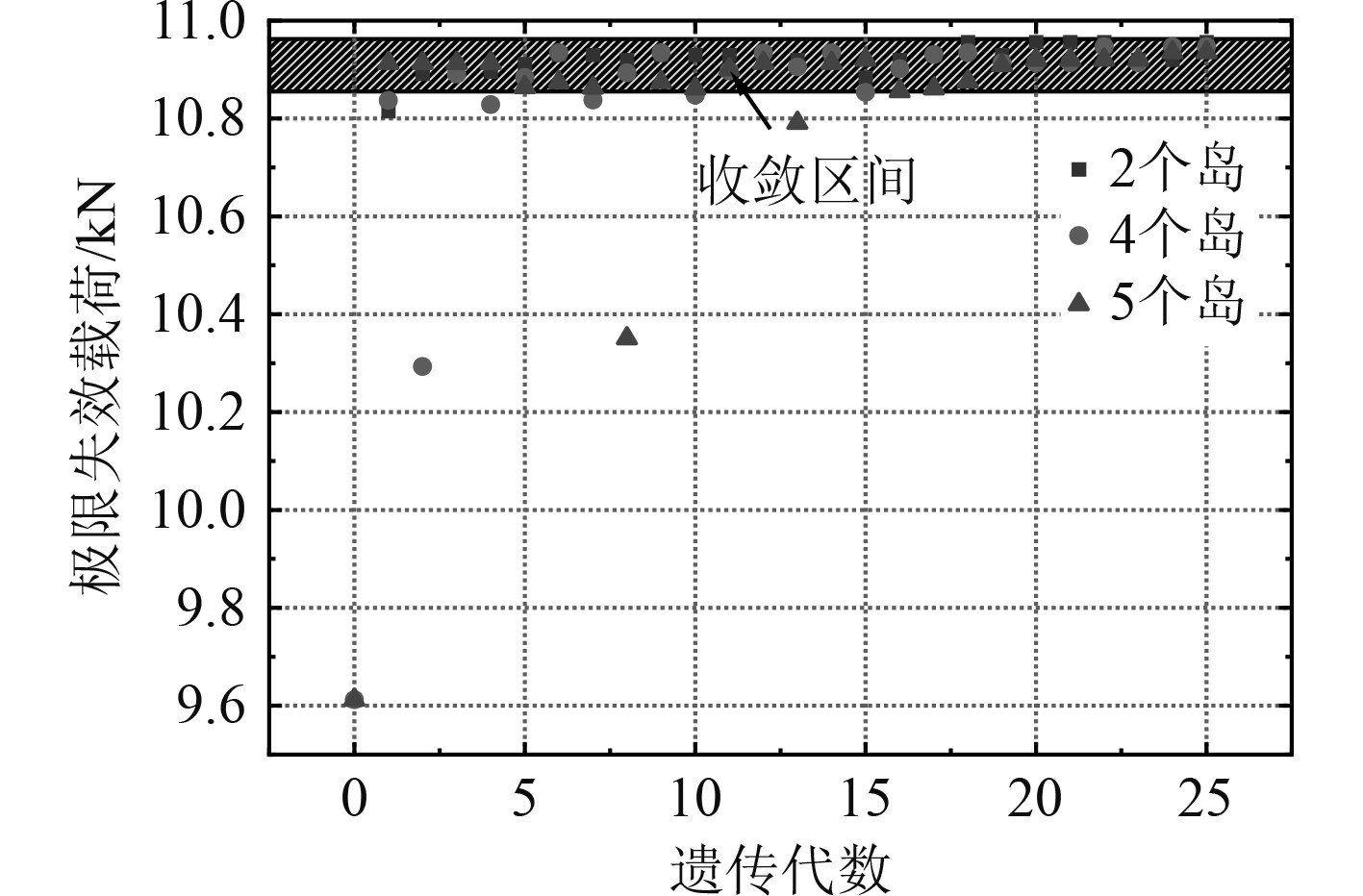
|
图 14 不同岛数下的单搭胶接结构铺层优化结果 Fig. 14 Optimization results of single-stack adhesive structure layups under different island counts |
可知,随着岛数的增大,遗传算法的结果越来越不稳定,岛数为2最后出现非收敛解为第1代,岛数为4最后出现非收敛解为第10代,岛数为5最后出现非收敛解为第13代,所以应该取较少的岛数进行研究。
5.2 交叉概率影响效应交叉概率越高,群体中新结构的引入越快,已获得优良基因结构的丢失速度也相应升高。而交叉概率太低则可能导致搜索阻滞。
根据表3的遗传算法参数设置,在其他参数不变的情况下,将交叉率改变,得到结果如图15所示。

|
图 15 不同交叉率下的单搭胶接结构铺层优化结果 Fig. 15 Optimization results of single-stack adhesive structure layups under different crossover rates |
可知,随着交叉率的增大,优良基因丢失概率增加。0.8交叉率最后出现非收敛解为第10代,0.9交叉率最后出现非收敛解为第12代,1.0交叉率最后出现非收敛解为第16代。由于迭代收敛较快,故可采用较低的交叉率来保证解的稳定性。
5.3 变异概率影响效应变异操作是保持群体多样性的有效手段,交叉结束后,交配池中的全部个体位串上的每位等位基因按变异概率随机改变。变异概率太小,可能使某些基因位过早丢失的信息无法恢复;而变异概率过高,则遗传搜索将变成随机搜索。
根据表3的遗传算法参数设置,在其他参数不变的情况下,将变异率改变,得到结果如图16所示。

|
图 16 不同变异率下的单搭胶接结构铺层优化结果 Fig. 16 Optimization results of single-stack adhesive structure layups under different rates of variation |
可知,随着变异率的增大,遗传算法的结果越来越不稳定,0.05变异率最后出现非收敛解为第1代,0.1变异率最后出现非收敛解为第16代,0.2变异率甚至无法在25代内收敛,而由于本文是一个较快收敛的优化问题,变异率增大带来的快速收敛的优势在本文优化中体现的不明显,所以本文取较小的变异率0.05进行研究。
6 结 语本文采用多岛遗传算法对载荷作用下的CFRP复合材料层合板单搭胶接结构连接强度,进行铺层方式优化,得到以下结论:
1)CFRP复合材料层合板胶接结构的剥离极限失效载荷与拉伸极限失效载荷成正比。
2)在铺层角度和铺层顺序被约束的情况下,CFRP复合材料铺层纤维方向为
3)遗传算法参数对优化效率及稳定性有一定影响,对于本文中可较快收敛的遗传算法优化问题应采用较少的岛数、较低的交叉率和较低的变异率保证其优化求解的快速性和稳定性。
| [1] |
唐玉玲. 碳纤维复合材料连接结构的失效强度及主要影响因素分析[D]. 哈尔滨: 哈尔滨工业大学, 2015.
|
| [2] |
王孝慧, 姚卫星. 复合材料胶接结构有限元分析方法研究进展[J]. 力学进展, 2012, 42(5): 562–571.
|
| [3] |
郭霞, 关志东, 刘遂, 等. 搭接长度对复合材料单搭接胶接接头的影响[J]. 科技导报, 2013, 31(7): 37–41.
|
| [4] |
毛振刚, 侯玉亮, 李成, 等. 搭接长度和铺层方式对CFRP复合材料层合板胶接结构连接性能和损伤行为的影响[J]. 复合材料学报, 2020, 37(1): 121–131.
|
| [5] |
Sülü İ Y. Mechanical behavior of composite parts adhesively jointed with the insert double-lap joint under tensile load[J]. Welding in the World, 2018, 62(2): 403-413. DOI:10.1007/s40194-017-0543-9 |
| [6] |
PARK J, HWANG J, LEE C, et al. Stacking sequence design of composite laminates for maximum strength using genetic algorithms[J]. Composite Structures, 2001, 52(2): 217-231. DOI:10.1016/S0263-8223(00)00170-7 |
| [7] |
郭琰, 黄斌, 钱征华. 基于遗传算法的开孔复合材料层合板铺层优化[J]. 玻璃钢/复合材料, 2018 (12): 5–10.
|
| [8] |
陆振玉, 张恩阳, 刘波. 基于改进自适应遗传算法的复合材料铺层优化设计[J]. 玻璃钢/复合材料, 2016 (2): 53–56.
|
| [9] |
胡春幸. CFRP层合板胶接结构性能研究及遗传算法优化[D]. 郑州: 郑州大学, 2021.
|
| [10] |
GUO W, XUE P, YANG J. Nonlinear progressive damage model for composite laminates used for low-velocity impact[J]. Applied Mathematics and Mechanics, 2013, 34(9): 1145-1154. DOI:10.1007/s10483-013-1733-7 |
| [11] |
BENZEGGAGH M L, KENANE M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus[J]. Composites Science and Technology, 1996, 56(4): 439-449. DOI:10.1016/0266-3538(96)00005-X |
| [12] |
梁祖典, 燕瑛, 张涛涛, 等. 复合材料单搭接胶接接头试验研究与数值模拟[J]. 北京航空航天大学学报, 2014, 40(12): 1786–1792.
|
| [13] |
中国航空研究院. 复合材料结构设计手册[M]. 北京: 航空工业出版社, 2001.
|
 2023, Vol. 45
2023, Vol. 45
