0 引　言

水动力噪声研究主要是为了降低舰船的水下噪声，水动力噪声根据其形成机理可归纳为流噪声和流激噪声两部分^[1]。舰艇中、高速航行时，声呐导流罩外边界层的壁面受脉动压力激励，引起罩壳结构振动，并向罩壳内辐射噪声，该噪声是声呐平台区自噪声的主要成分^[2]，流激振动噪声严重影响了声呐基阵的正常工作，制约了舰船中高来流速度下的作战能力。

传统的透声窗结构常用单层玻璃钢结构，舰船在低Mach数下，流体对结构振动及声辐射影响较小，单层玻璃钢结构能满足工作要求。但较高航速下，湍流边界层（Turbulent Boundary Layer）激励结构振动声辐射更大，为了降低流激振动噪声的影响，有必要对TBL激励结构振声问题进行研究。随着对船舶领域的关注，国内舰船水声透声材料、减振结构等相关研究也相继开展^[3-5]。梅志远等^[6]开展了湍流激励下橡胶贴敷声呐罩自噪声抑制机制研究；胡昊灏等^[7]基于三阶剪切变形理论，研究了水下复合层矩形板水下声辐射问题；李华东^[8]进行了静水力作用下夹芯结构的力学性能规律研究；陈美霞等^[9]研究了湍流激励下结构振动特性的半解析半数值算法。夹芯透声窗具有插入损失小、阻尼因子大、比强度高等优点。而夹芯型结构的设计，需要综合考虑到透声窗的透声性能和湍流脉动压力激励在导流罩内基阵部位产生的自噪声。当前对湍流激励降噪机理与理论算法研究已经有了一定进展，对于结构透声性能或者流激振声特性也有一定研究成果，但现阶段在实际工程应用方面，透声窗结构性能有着更大的要求，因此结合透声窗结构的工作环境，还需开展能同时满足透声和流激振声特性的透声窗结构研究。

水声常用材料包括玻璃钢、碳纤维复合材料（CFRP）、铝合金、橡胶等。CFRP较传统材料而言，比强度（强度/密度）高、比模量高、质量轻、抗疲劳性能好且减振性能优良^[11]。铝合金强度高、刚性好，比强度远大于钢等其他金属结构材料，低温性能好、质量轻^[12]，以上2 种材料运用于舰船首部能提供结构强度。橡胶材料作为阻尼层一般依靠横波传播截止效应抑制湍流脉动压力水动力学成分所致的壳板自噪声，降噪量高低与厚度模态有关，同时可以保持声波高透射^[3]。因此，通过合理铺设以上材料，应该能得到一种透声性能良好、流激振声特性优于传统玻璃钢结构的多层透声窗结构。本文拟采用CFRP、铝合金与橡胶3 种材料，构成一种碳-铝橡胶透声窗结构，利用有限元法，验证了碳-铝橡胶透声窗在具备与传统玻璃钢橡胶结构相近的良好透声性能下，兼顾了更好的流激振声特性，比传统玻璃钢橡胶制透声窗辐射噪声更小，降噪效果更好，为碳-铝橡胶透声窗在舰船上的推广应用提供了数值计算依据。

1 透声及流激振声计算方法 1.1 透声性计算

本文主要利用有限元法对平板结构透声性能进行分析计算。基于声的波传递理论，推导夹层结构透射系数计算公式^[13]。

依据Helmhotz方程，声压和声波振速的表达式分别为：

$ \begin{split} &{P_i} = {A_i}{e^{ - ikix}} + {B_i}{e^{ikix}}，\\ & {u_i} = \frac{1}{z}\left[ {{A_i}{e^{ - ikix}} - {B_i}{e^{ikix}}} \right] \end{split} 。$

(1)

式中： $A$ 、 $B$ 均为常数； ${k_i}$ 为波数， ${k_i} = {\omega _i}/{c_i}$ ； ${z_i}$ 为介质的特性阻抗， ${z_i} = {\rho _i}{c_i}$ ， $i = 1,2...n$ ，根据设计夹层数量选取 $i$ 层层数代入上式计算。

求解上述方程组可得透声系数 ，用来表征透声夹层结构透声性能。

1.2 流激振动噪声

对于声振耦合问题常采用有限元法（Finite Element Method），对结构和流体进行单元离散，可得矩阵形式的流体波动方程为：

$ {\boldsymbol{M_e^f}}{\ddot p_e} + {\boldsymbol{K_e^f}}{p_e} + {\rho _0}{\boldsymbol{R_e^f}}{\ddot u_e} = \varPhi 。$

(2)

式中： ${\boldsymbol{M_e^f}} =\displaystyle \frac{1}{{{c^2}}}\iiint\limits_V {N{N^{\rm{T}}}{\rm{d}}V}$ 为流体质量矩阵； ${\boldsymbol{K_e^f}} =\displaystyle \iiint\limits_V {{B^{\rm{T}}}B{\rm{d}}V}$ 为流体刚度矩阵； ${\boldsymbol{R_e^f}} =\displaystyle \iint\limits_S {N{n^{\rm{T}}}{N^{\rm{T}}}{\rm{d}}S}$ 为流体面上的耦合矩阵。

在流体与结构的交界面上，声压对结构同时也产生一个面力的作用，将其变换到节点上，则结构方程可写为：

$ {\boldsymbol{M_e^s}}{\ddot u_e} + {\boldsymbol{C_e^s}}{\dot u_e} + {\boldsymbol{K_e^s}}{u_e} = {\boldsymbol{F_e^s}} + {\boldsymbol{F_e^f}}。$

(3)

式中： ${\boldsymbol{F_e^f}} = {\boldsymbol{R_e^{f{\rm{T}}}}}{p_e}$ 为流体对结构的作用力； ${\boldsymbol{M_e^s}}$ 为结构的质量矩阵； ${\boldsymbol{K_e^s}}$ 结构的刚度矩阵； ${\boldsymbol{C_e^s}}$ 结构阻尼矩阵。

用统一的矩阵形式表示，有

$ \begin{split}&\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{M_e^s}}}&0 \\ {{{\boldsymbol{\rho}} {\boldsymbol{{R_e^f}}}}}&{{\boldsymbol{M_e^f}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\ddot u}_e}} \\ {{{\ddot p}_e}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{C_e^s}}}&0 \\ 0&{{\boldsymbol{C_e^f}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\dot u}_e}} \\ {{{\dot p}_e}} \end{array}} \right\} + \\ &\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{K_e^s}}}&{ - {{{\boldsymbol{R_e^f}}}^{\rm{T}}}} \\ 0&{{\boldsymbol{K_e^f}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_e}} \\ {{p_e}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{F_e^s}}} \\ 0 \end{array}} \right]。\end{split} $

(4)

式中， $C_e^f$ 为声阻尼矩阵。

基于FEM法计算结构流激振动声辐射，其流程为：首先通过有限元软件对透声窗结构模型以及流体域进行离散建模，利用大涡模拟方法计算结构表面湍流脉动压力并加载至声振耦合模型中，求解透声窗结构流激振动噪声规律。

2 算例验证及计算分析 2.1 透声性分析可靠性验证

首先对透声性计算进行验证，以铝合金为例，首先对夹芯平板的透声性计算内进行验证，芯层材料为橡胶，两侧为钛板，形成橡胶夹芯结构。保持总厚度20 mm不变，两侧钛板厚度依次为1 mm、2 mm、3 mm，橡胶夹芯依次为18 mm、16 mm、14 mm时，计算铝合金橡胶夹芯结构透声系数。

如图1所示，将文献结果与本文计算结果对比，在10000 Hz时透声系数最大误差为0.43%，可见曲线结果吻合良好，验证了本文数值方法的有效性。

2.2 透声性能计算

基于有限元法对声波垂直透过橡胶层合板结构进行透声性能计算，分析不同类型、不同材料等参数的透声系数变化规律。

建立0.2 m×0.2 m×1 m的板结构有限元模型，如图2所示。划分声学有限元网格，大小满足 $L \leqslant {c / {6{f_{\max }}}}$ ，其中 $ c $ 为水中声速1500 m/s， $ {f_{\max }} $ 为计算最大频率1000 Hz，即遵循一个波长至少包涵6 个网格单元的原则，选择网格大小为0.01 m，以海水为声场介质，设定声-结构边界、完美匹配层等边界条件，施加垂直入射的平面波声源，分析计算不同类型平板的透声性能。

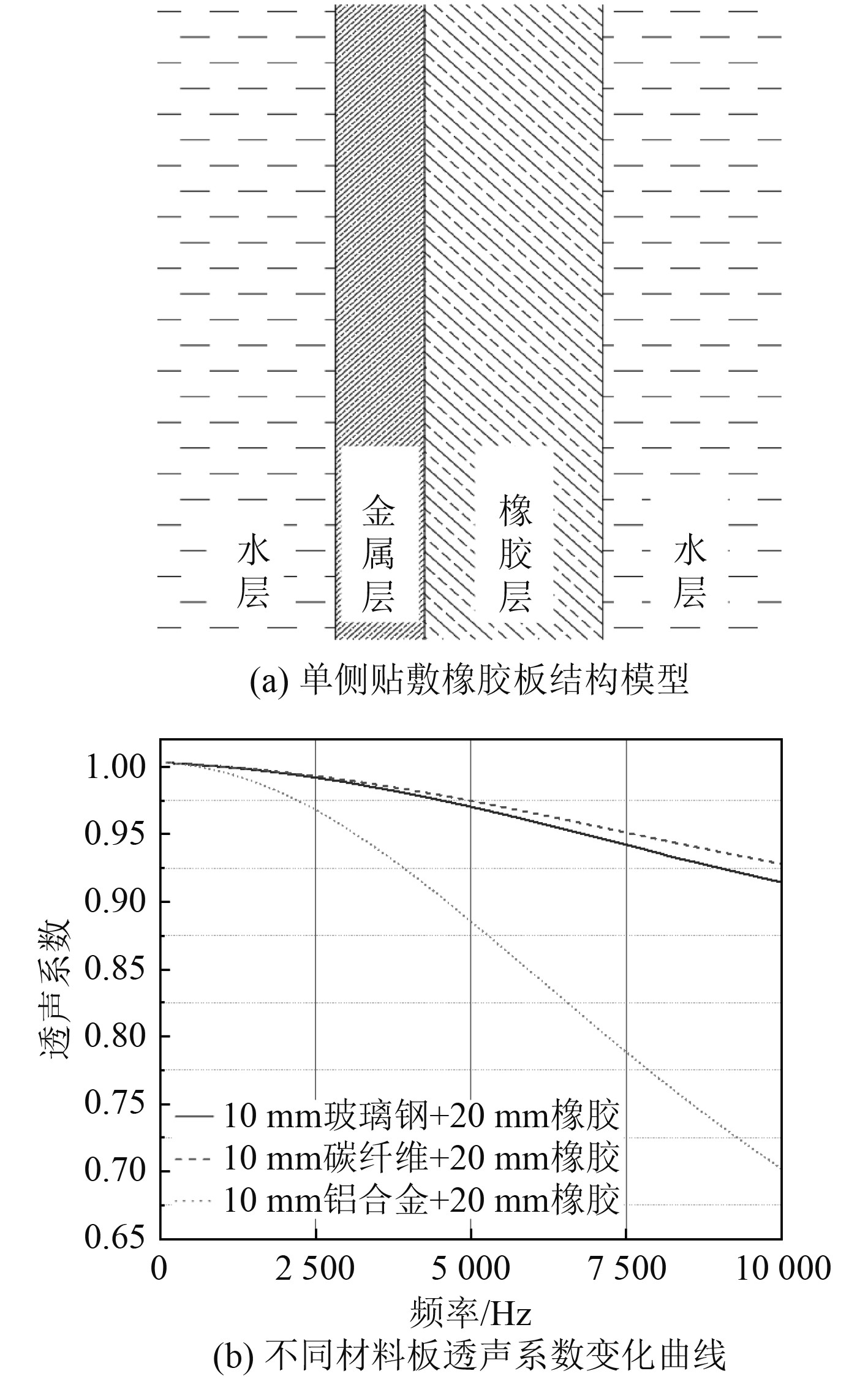
首先设置等厚度10 mm玻璃钢、碳纤维、铝合金材料单侧贴敷20 mm橡胶时，计算3 种不同材料板的透声性能。透声系数对比曲线如图3所示。

可知，在0～10000 Hz范围，单侧贴敷橡胶的各平板透声系数均随着频率的增大而减小；相同10 mm厚度，透声系数由大到小以此为：碳纤维＞玻璃钢＞铝合金，碳纤维比玻璃钢透声系数略优，两者曲线较为接近，但都远大于铝合金，在10000 Hz时三者透声系数值分别达到0.914、0.928、0.702，铝合金板降幅最明显，碳纤维板与玻璃钢板降幅较小。

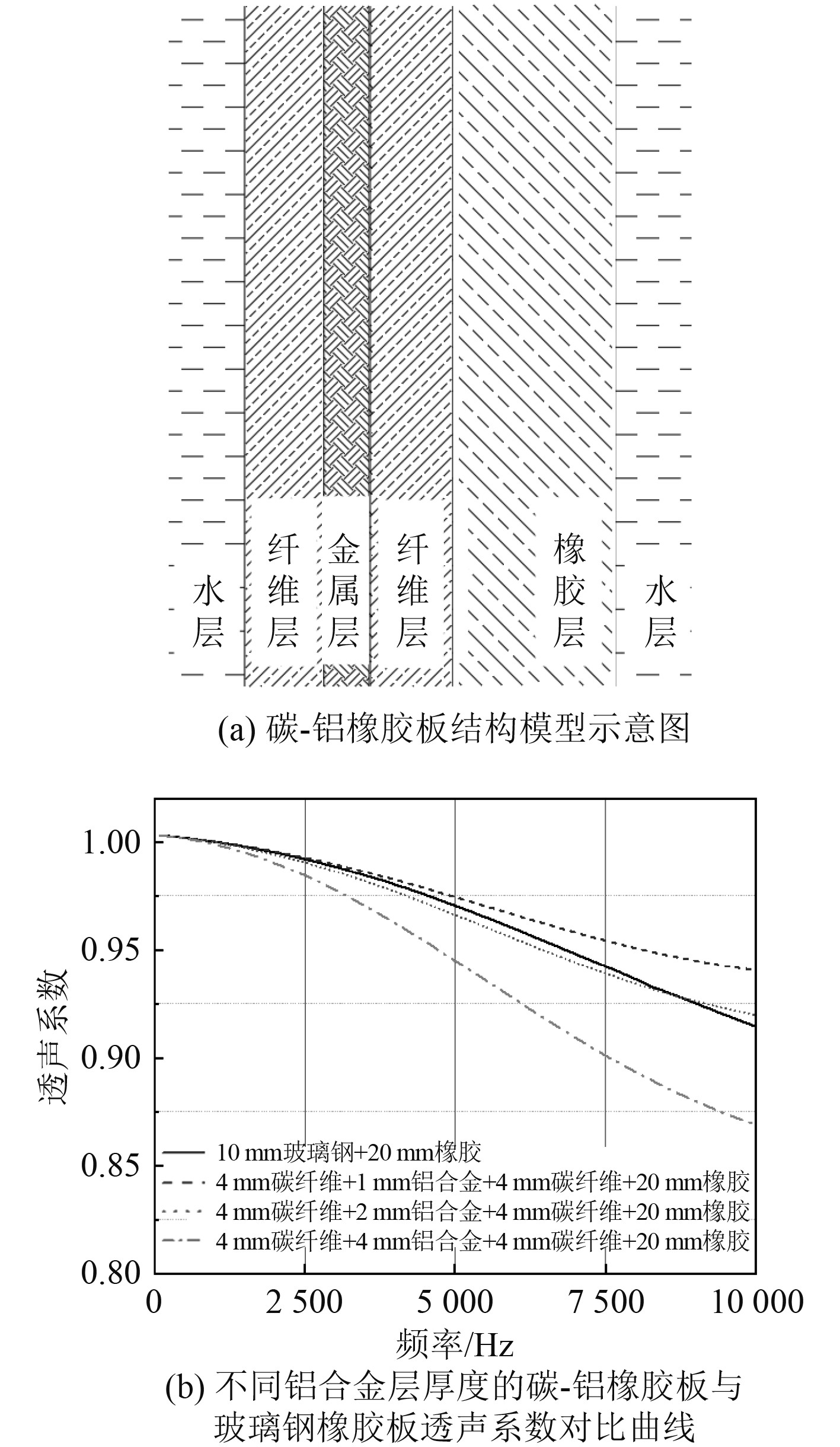
考虑到铝合金结构优异的力学性能，综合透声性能要求，选择碳纤维、铝合金与橡胶材料，设计碳-铝橡胶板。将10 mm玻璃钢贴敷20 mm橡胶结构板作为比较对象，以达到等厚度传统玻璃钢橡胶结构透声性能为目标，优化二者厚度配比，基于结构对称设计及碳纤维透声性能较好的前提，通过改变铝合金层厚度，比较在不同铝合金层厚度下，碳-铝橡胶板与等厚传统单层玻璃钢单侧贴敷橡胶板二者的透声系数变化情况，确定合适的铺层厚度。

如图4所示，在0～10000 Hz范围内，随着频率的升高，碳-铝橡胶板与玻璃钢橡胶板透声性曲线均呈现下降趋势；铝合金层厚度为1 mm与2 mm时，碳-铝橡胶板优于玻璃钢橡胶板透声系数，以玻璃钢橡胶板透声性能为参照，在符合透声性能要求的前提下，结构厚度增加，减振效果通常更好，即铝合金厚度为2 mm工况，因此选择4 mm碳纤维+2 mm铝合金+4 mm碳纤维+20 mm橡胶，综合透声性计算结果表明；碳-铝橡胶板在工作频率范围内可以达到与传统玻璃钢橡胶板相似的透声性能，满足实际工程应用要求，因此还需要进一步探究碳-铝橡胶板流激振动特性。

3 流激振声特性计算 3.1 振动模态分析验证

首先验证结构模型计算可靠且结果准确。选择夹芯结构，即验证夹芯结构自身模态，进行夹芯模型固有频率计算。选择文献[14]中四边简支双层铝橡胶夹芯结构，铝板结构长宽均为0.348 m、0.3048 m，上、下层铝板厚度均为0.000762 m，橡胶层厚度为0.000254 m。表1为模态计算结果与文献解析解对比结果。可知，本文铝橡胶夹芯板模态计算结果与文献解析解最大误差为1.4%，平均误差为1.04%，表明夹芯结构建模计算准确。

3.2 流激振动噪声特性计算

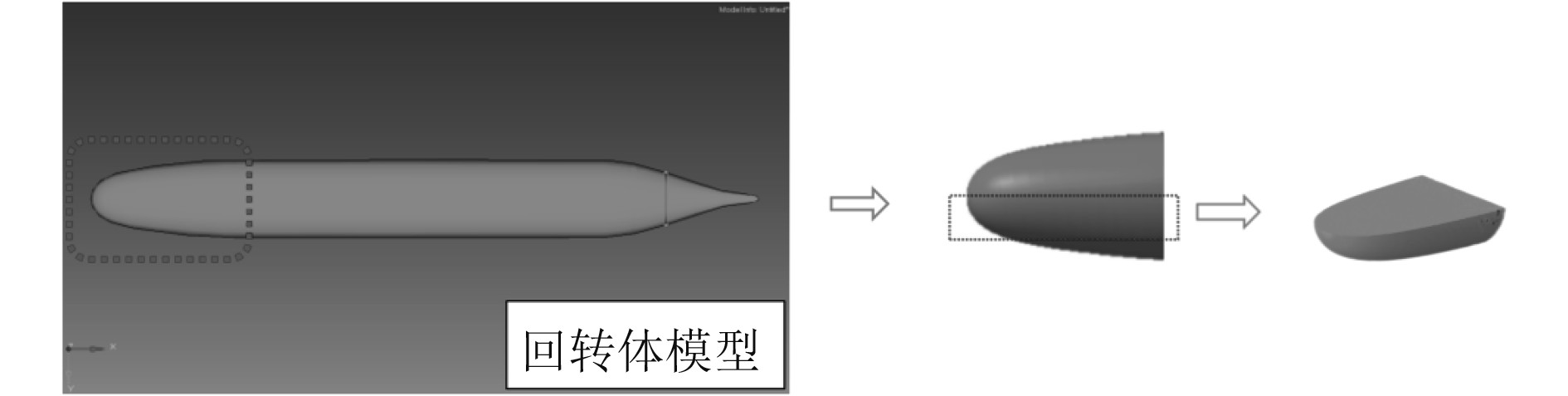
建立水下航行体导流罩模型，沿船长方向截取首部0.6 m区域回转体椭球部，0.6 m处直径为0.44 m。将橡胶层合板形式应用于水下航行体导流罩透声窗部位，加载结构表面湍流脉动压力并计算振声响应。为方便查看透声窗区域结构及内部声压情况，主要针对z方向0～0.15 m透声窗区域展示声呐罩透声窗结构振速云图及内部声场声压云图，如图5所示。

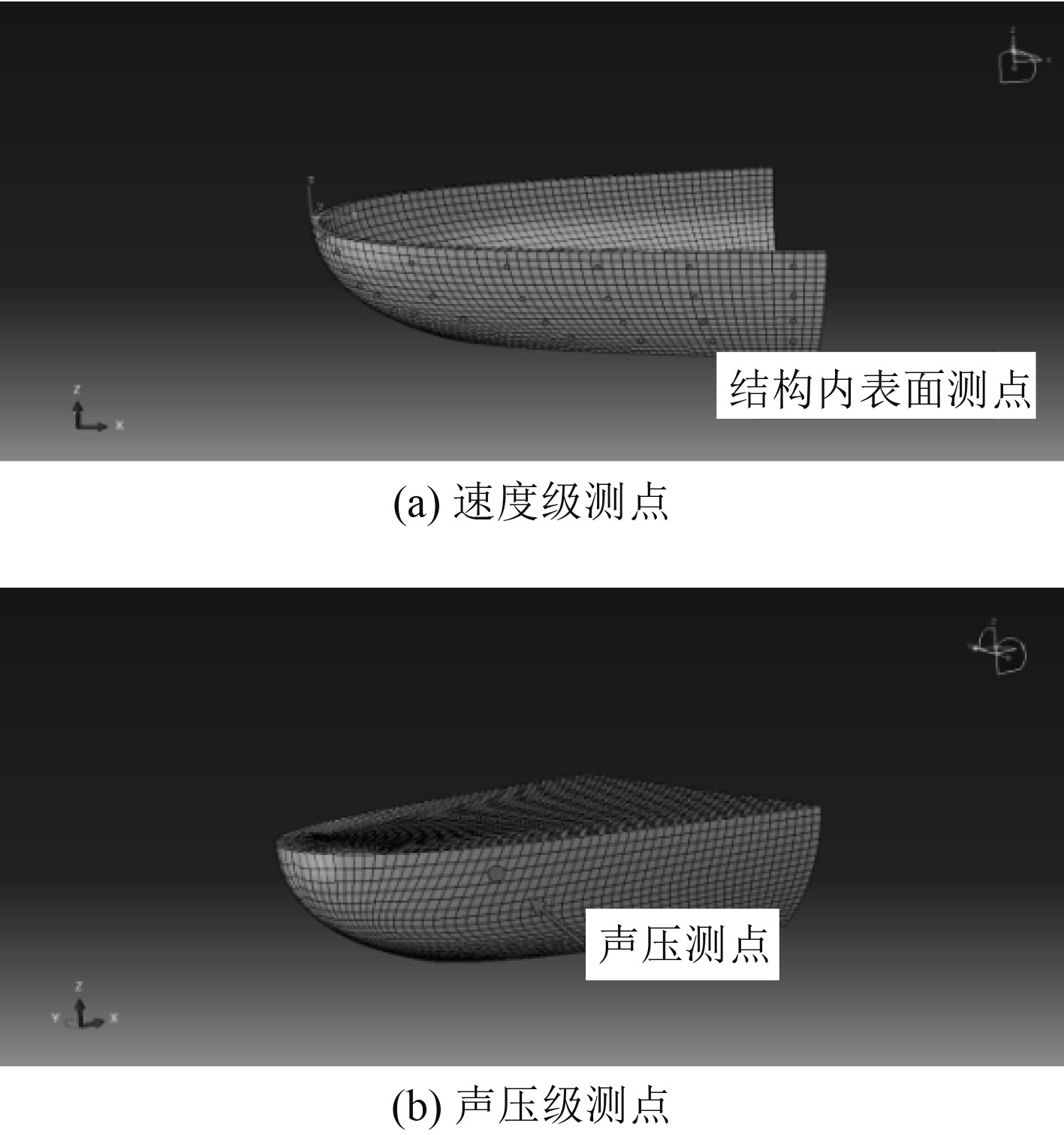
因此，在透声窗部位设置各测点，提取测点数据，分析不同形式结构流激振声特性。透声窗结构表面振速及声场声压测点位置选取如图6所示。

在透声性计算结果基础上，保持结构厚度一致，选用碳-铝橡胶结构（4 mm碳纤维+2 mm铝合金+4 mm碳纤维+20 mm橡胶结构）与传统玻璃钢单侧贴敷橡胶结构（10 mm玻璃钢+20 mm橡胶）对比，在正向来流速度为5 m/s时，计算上述碳-铝橡胶形式透声窗与传统玻璃钢橡胶形式透声窗结构内部测点接收辐射声压曲线变化规律，对比2 种类型声呐罩透声窗结构的流激振声性能。

图7为声呐罩透声窗受TBL激励下结构表面振速云图，图8为透声窗声腔声压云图。表明结构表面振速最大值与较大值时刻变化，造成内场声腔中结构振动辐射噪声声压最大值分布呈现一定随机性。

由图9可知，来流速度为6 m/s时，对比碳-铝橡胶结构与传统玻璃钢橡胶结构，发现两者测点处声压曲线均随频率升高而降低，声压在计算区间范围内趋势与激励谱趋势一致，声压级对比曲线趋势基本相似，2 条曲线相差约14 dB左右，且碳-铝橡胶结构比统玻璃钢橡胶结构声压值更小。可得出结论，6 m/s流速下，碳-铝橡胶形式透声窗结构被激振动更轻微，降噪效果更好。

3.3 来流速度对流激振声特性影响

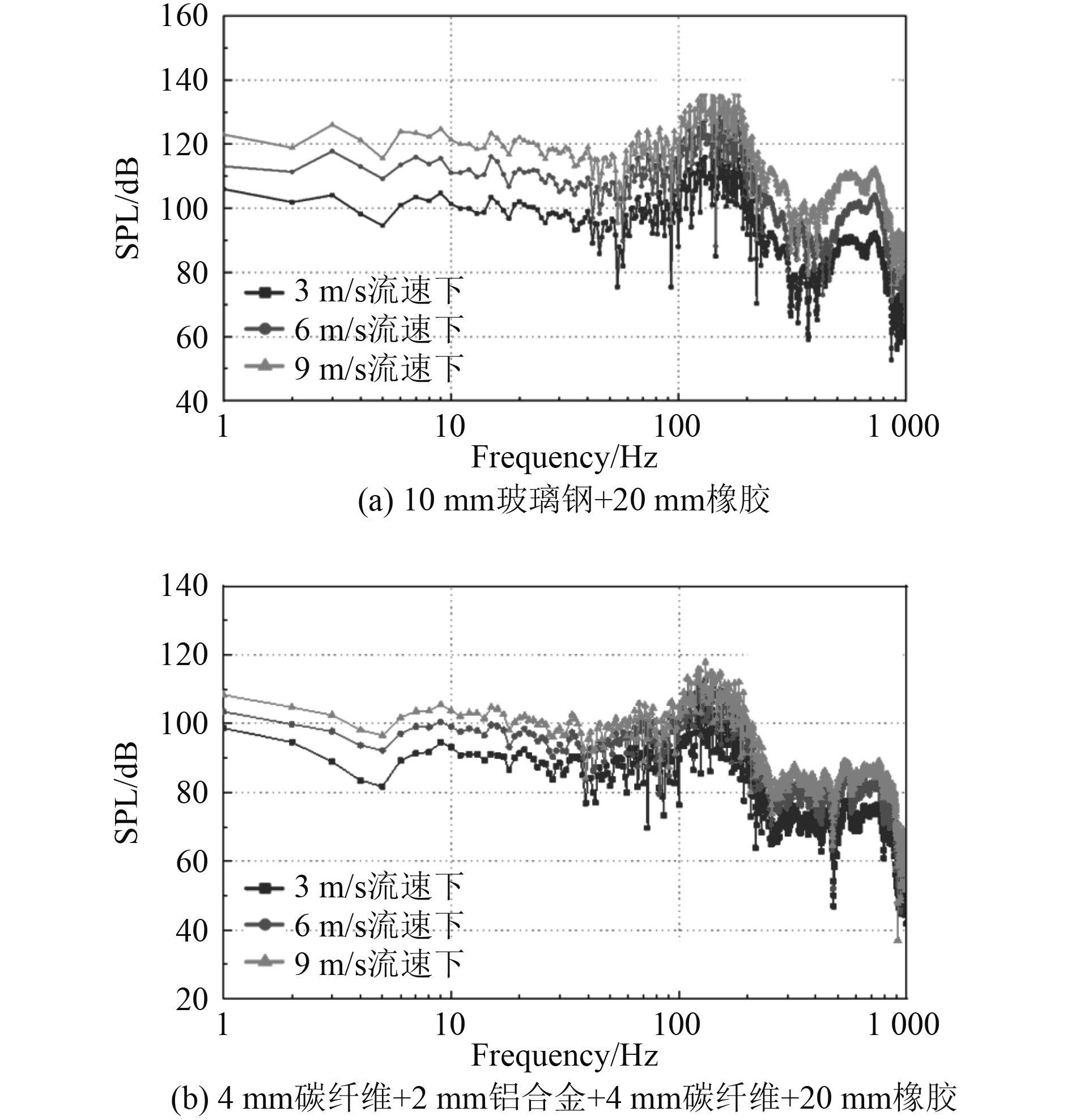
分析流速度分别为3 m/s、6 m/s和9 m/s时，传统玻璃钢橡胶形式与碳-铝橡胶形式透声窗结构流激振动噪声结果，如图10所示。

可知，随着频率升高，测点声压级从大到小依次为3 m/s、6 m/s、9 m/s，3 条曲线响应趋势一致，测点声压级随来流速度升高依次递增，逐级均相差7～8 dB。分析原因为来流速度越高，湍流脉动压力越大，声呐罩透声窗振动越剧烈，流激振动辐射噪声值也越大，测点声压也就越大，与传统玻璃钢贴敷橡胶形式相比，碳-铝橡胶结构表面振动剧烈程度在所测3种航速下均小于前者，表明碳-铝橡胶形式比传统玻璃钢橡胶形式抑振降噪能力更优异，拥有良好的振声特性。

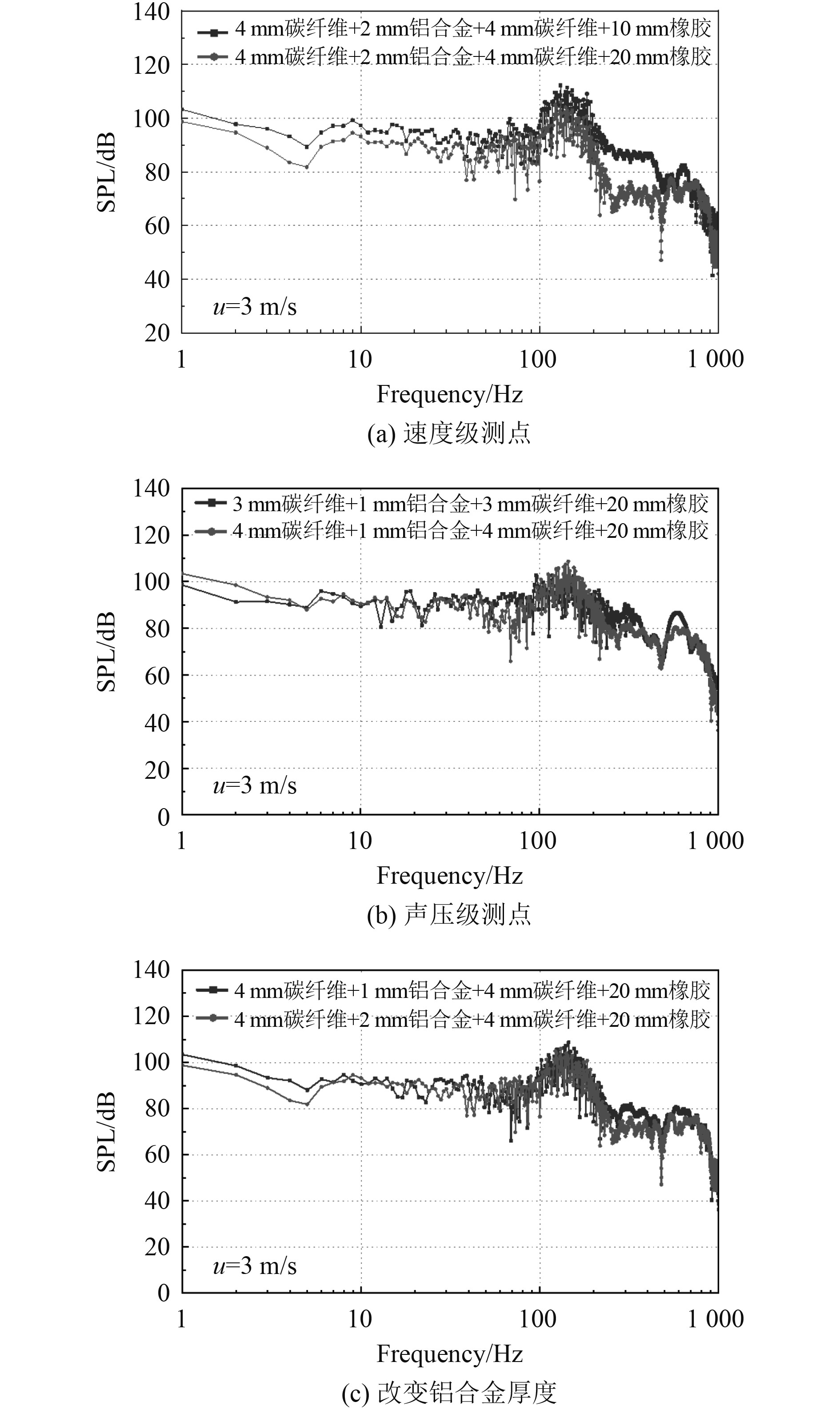
3.4 铺层厚度对流激振声特性影响

改变碳纤维、铝合金、橡胶铺层厚度，探究声呐罩透声窗结构流激振动噪声影响规律。以碳-铝橡胶结构为例（4 mm碳纤维+2 mm铝合金+4 mm碳纤维+20 mm橡胶），保持其余铺层厚度不变，仅改变橡胶阻尼层厚度为5 mm、10 mm时，计算透声窗结构流激振动噪声，对比结果如图11（a）所示。改变左右层碳纤维层厚度各为3 mm、4 mm时，计算透声窗结构流激振动噪声，对比结果如图11（b）所示。改变铝合金层厚度为1 mm、2 mm时，计算透声窗结构流激振动噪声，对比结果如图11（c）所示。

可知：不同铺层材料厚度对流激振动辐射噪声影响较大，随着计算频率的升高，加厚橡胶层、碳纤维层、铝合金层厚度，声压曲线均有下降，在中低频尤为明显；结构振动幅度越小，产生的辐射噪声越小，结构抑振性能越优异。

4 结　语

本文针对碳-铝橡胶形式结构的透声及振声特性，首先利用有限元法对结构透声性进行计算，然后加载湍流脉动压力计算声呐罩透声窗结构流激振动噪声，并与传统玻璃钢橡胶形式对比。最后探究不同厚度、不同来流速度等因素影响下透声窗结构流激振声规律。得出以下结论：

1）在10000 Hz范围内，不同材料透声性能从优到劣依次为碳纤维、玻璃钢、铝合金；从透声性角度分析，碳-铝橡胶板具有媲美等厚度传统玻璃钢橡胶板的透声性能。

2）不同来流速度为3 m/s、6 m/s和9 m/s下，随着流速的增大，引起的声呐罩结构流激噪声逐步递增，响应趋势基本相似，声压级逐级增加8 dB左右。

3）适当加厚橡胶层、碳纤维层及铝合金层，碳-铝橡胶透声窗结构被激振动的幅度减小，辐射噪声值降低，结构抑振能力提高，符合振动响应规律。

4）通过透声与振声特性分析，碳-铝橡胶形式比传统玻璃钢橡胶形式透声窗结构减振降噪能力更优异，拥有更好的振声特性，为声呐罩透声窗结构设计提供数值依据。