在有限元计算中,网格大小对计算精度有较大影响,为了得到某些特定部分更加精确的计算结果而又不影响模型整体的计算效率,此时常常需要对这些特定部分进行局部结构分析。局部结构分析中最常用的是子模型法[1]。子模型法是一种基于整体分析结果的局部分析方法,主要是对整体模型进行局部切割得到一个可以进行单独分析的子模型,再通过更精细的网格划分来实现对局部区域更加精细的分析[2-4]。切割后生成的子模型、子模型边界的位移信息、子模型内部的载荷信息一起构成了子模型的分析模型[5]。该方法可以大大减少对无关区域的分析而把主要的精力汇聚在所关心的局部区域,既节约了计算量也提高了关心区域的计算精度。苏罗青等[6]采用子模型技术对船体贯穿式大开口处的角隅结构进行优化分析,设计变量为角隅的形状及嵌入板的板厚,建立了一系列的局部角隅子模型进行有限元计算,得到了设计变量和结构Mises应力之间的变化规律,为类似的贯穿式大开口角隅结构的设计提供了有益参考。郭磊磊等[7]采用子模型方法对大型薄壁结构模型进行了对比分析,证明了子模型方法可以有效减少计算时间,提高计算精度,有一定的优越性。张志兴等[8]基于子模型方法对钢拱桥关键桥段进行精细化分析,结合最不利工况对关键桥段进行静力分析,得出各构件应力范围,为局部结构的精细化设计提供了有益参考。孙倩等[9]建立了同心圆及准同心圆式耐压液舱结构的有限元分析模型,编程并实例检验了其有限元程序的正确性,其程序可单独作为一个模块来取代复杂的解析法进行应力分析与优化设计。李坤宏等[10]结合CREO、Hypermesh、Ansys对船舶舱壁上的肋骨进行了强度分析及优化设计。本文以典型外置式耐压液舱为研究对象,采用子模型方法对耐压液舱应力梯度较大的部位进行精细化分析及变刚度设计,为耐压液舱结构的优化设计提供参考。
1 耐压液舱结构设计方案校核 1.1 耐压液舱结构设计方案耐压液舱结构基本尺寸如下:耐压液舱半径R1/R*=1.3,耐压船体半径R/R*=1.125,液舱壳板厚度t1/t*=1,减薄量Δt/t*=0.045,耐压船体壳板厚度t/t*=2.3,减薄量Δt/t*=0.06。液舱壳板上相邻纵骨间距b1/l*=0.8,实肋板间距l/l*=1.4。实肋板厚度t2/t*=0.9,舱壁板厚度dt/t*=1.0,纵向隔板厚度t3/t*=1.3,减薄量均为Δt/t*=0.045。其中:R*为基准半径,t*为基准厚度,l*为基准间距。纵骨T型材尺寸⊥
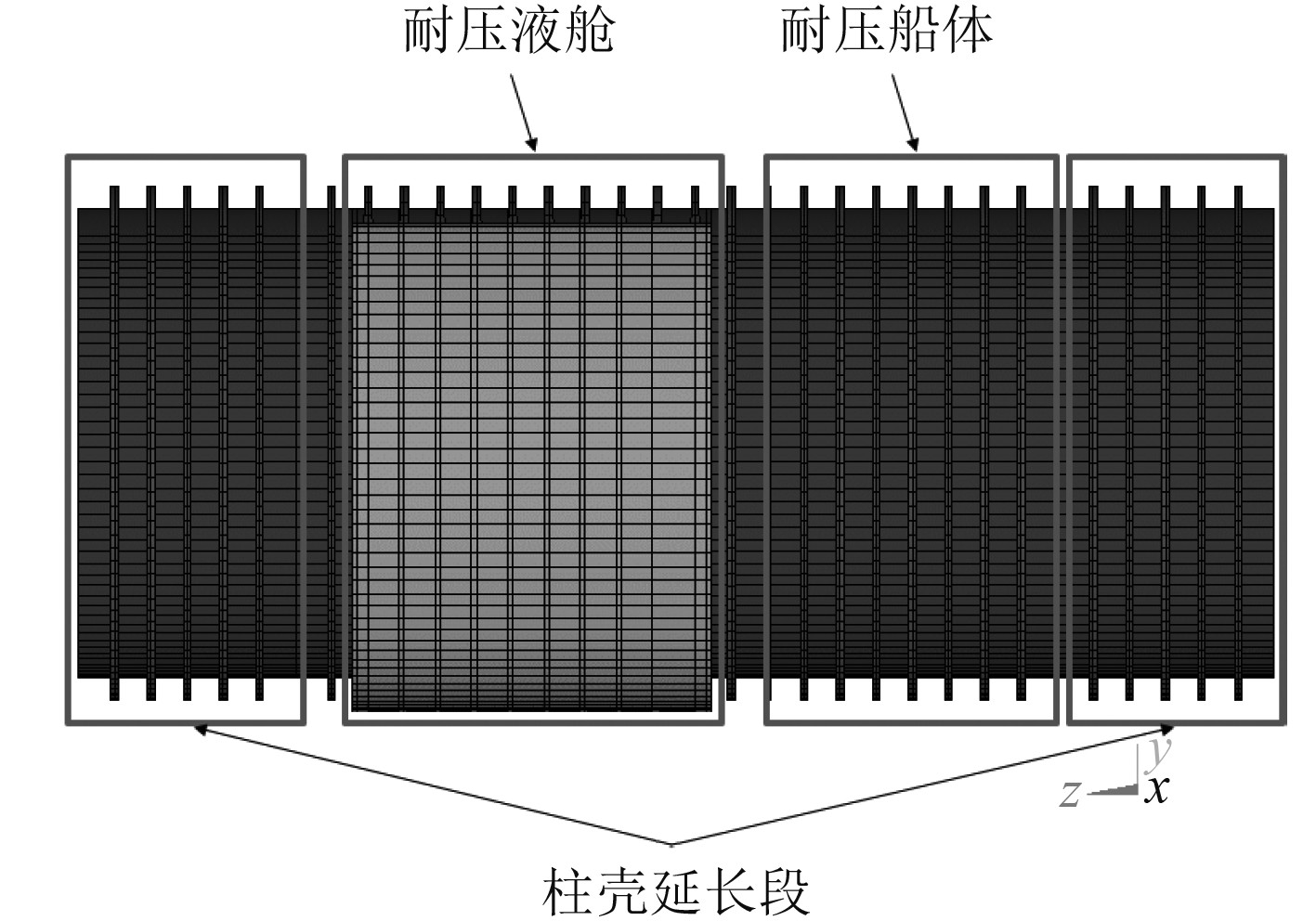
在笛卡尔坐标系下,沿船长方向为Z向,以向船首为正;耐压船体的船宽方向为X向,以向船体右舷为正;耐压船体的垂向为Y向,以向上为正;耐压船体圆柱壳分别向两端各延伸5档肋位,建立耐压液舱的整体几何模型,如图1所示。
|
图 1 几何模型 Fig. 1 Geometric model |
采用理想弹塑性材料,其泊松比取0.3,弹性模量取196 GPa,密度取7 850 kg/m3。纵骨、实肋板及径向加强筋屈服强度为590 MPa,其余构件屈服强度为850 MPa。
整体结构除纵骨T型材面板、实肋板径向加强筋T型材面板、纵向隔板T型材面板及横舱壁T型材面板采用梁单元Beam188外,其他结构均采用壳单元Shell181模拟。整体模型网格大小约为65 mm,壳单元共有464 327个,梁单元共有16 049个。
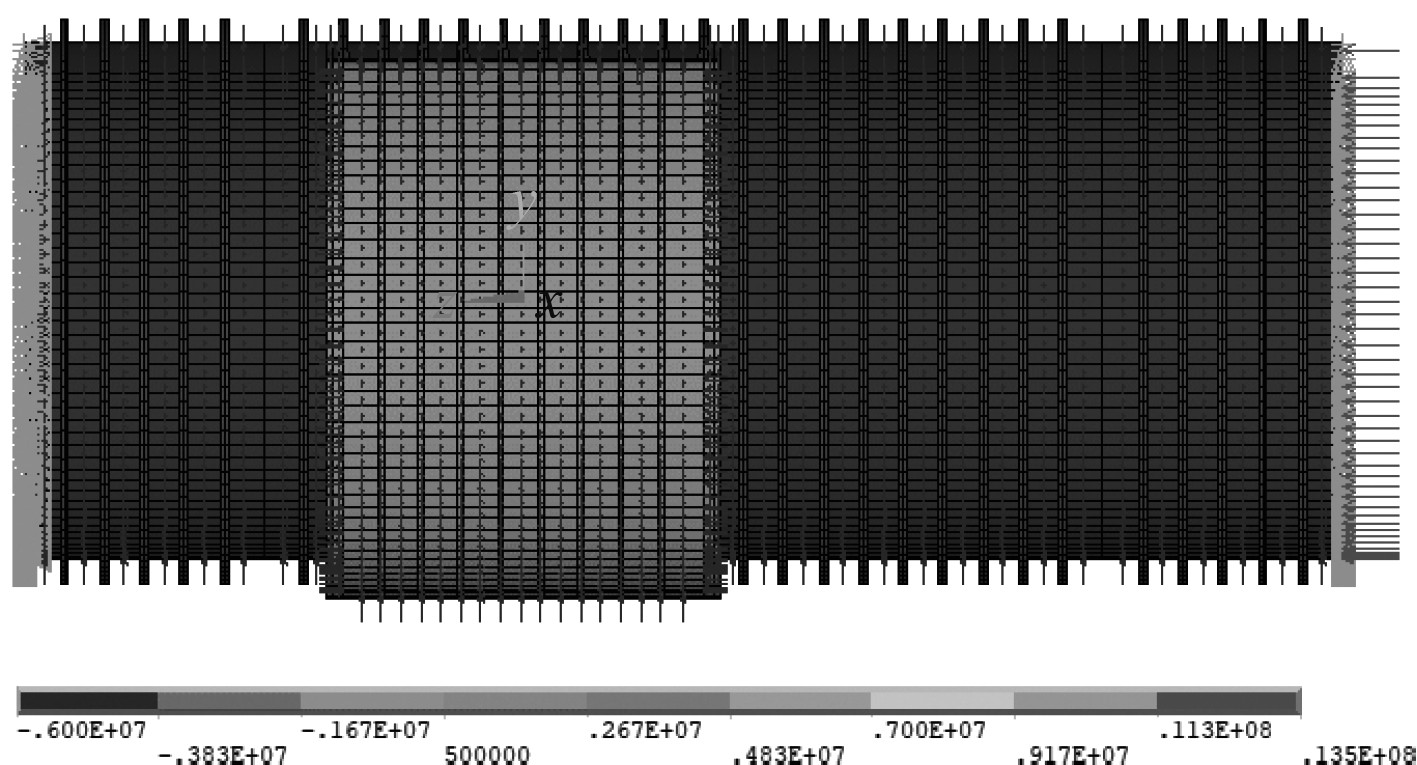
对耐压液舱进行力学分析时,计算压力取Pc/P*=1.2,P*为基准压力。考虑控制液舱设计的空舱工况,即外压施加于液舱壳板、液舱端部横舱壁及除液舱区域外的耐压船体壳板。作用在耐压船体端部的压力等效为在耐压船体壳板右端圆周线上施加的线压力,大小为Pl/Pl*=1.35,Pl*为基准线压力。舱段柱壳左端约束X、Y、Z三个方向的平动自由度,右端约束X、Y两个方向的平动自由度。载荷及约束如图2所示。
|
图 2 载荷及边界条件 Fig. 2 Load and boundary conditions |
在空舱工况下初始结构方案的规范及有限元计算结果如表1所示,其应力云图如图3所示。此外,经有限元计算发现纵骨自由翼缘上的总应力在实肋板根部与横舱壁根部有较大不同,即有限元计算中可体现不同位置纵骨之间的差别。而规范中的实肋板根部纵骨自由翼缘上的总应力无法体现上述不同部位的差别,故在校核结果时增加横舱壁根部纵骨自由翼缘上的总应力这一特征量。
|
|
表 1 初始方案耐压液舱结构应力计算结果 Tab.1 Stress results of pressure tank for initial scheme |

|
图 3 初始方案结构应力云图 Fig. 3 Stress nephogram of the initial scheme |
由表1可知,各项应力均满足规范要求,但如下区域有限元结果与规范值差异较大:
1)实肋板跨中纵骨根部壳板内表面周向应力的规范结果为−831.77 MPa,有限元结果为−693 MPa,二者相差20.02%。考虑到其应力梯度较大而液舱及耐压船体壳板网格大小为65 mm,此网格过大不足以得到精确解,故拟进一步采用子模型方法进行局部高应力的精细化分析。
2)实肋板根部纵骨自由翼缘上总应力的规范结果为−330.32 MPa,有限元结果为−534 MPa,二者相差−38.14%。横舱壁根部纵骨自由翼缘上总应力的规范结果为−330.32 MPa,有限元结果为−418 MPa,二者相差−20.98%。进一步观察可得此处高应力应力集中程度十分大,这是由于实肋板对中跨纵骨有较强的支撑及约束作用故实肋板根部纵骨自由翼缘处存在明显的局部应力集中情况。而端跨纵骨刚度在横舱壁处不连续,且横舱壁径向加强筋的弯曲对端跨纵骨变形有影响导致横舱壁根部纵骨自由翼缘处存在明显的局部应力集中情况。故可考虑增加肘板来降低纵骨自由翼缘上的应力。
若需得到以上所述部位的有限元精确解,网格需加密至很小的量级,这将导致整体模型网格量剧增,故后续将采用子模型方法进行局部高应力的精细化分析。
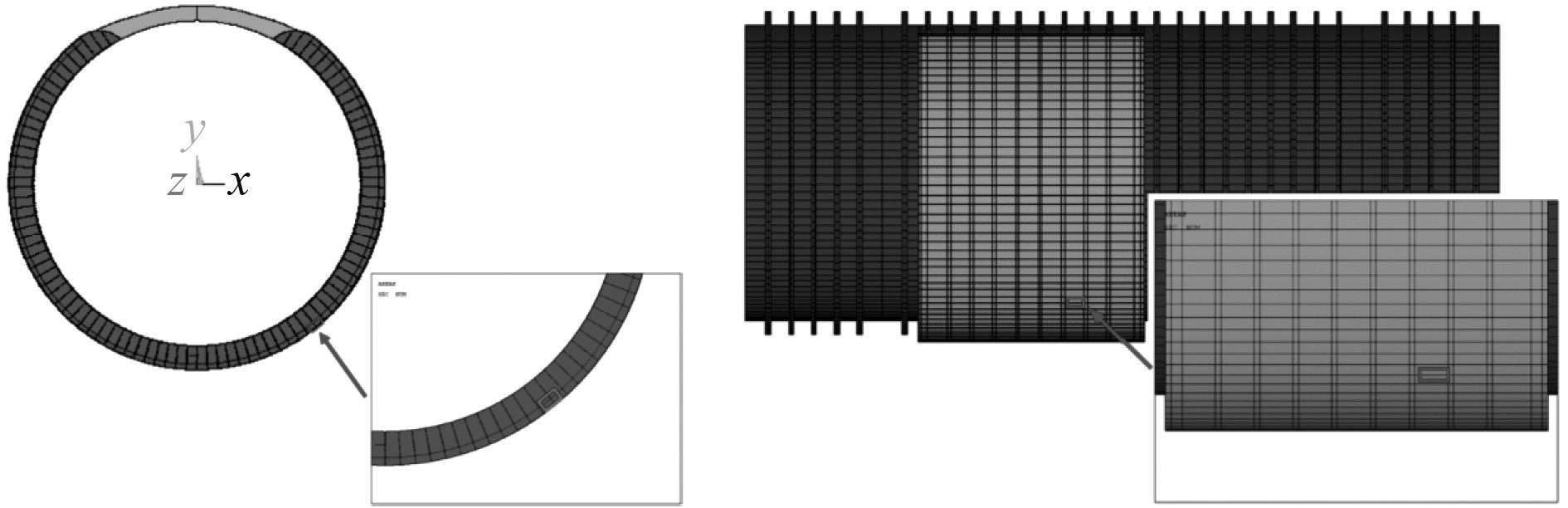
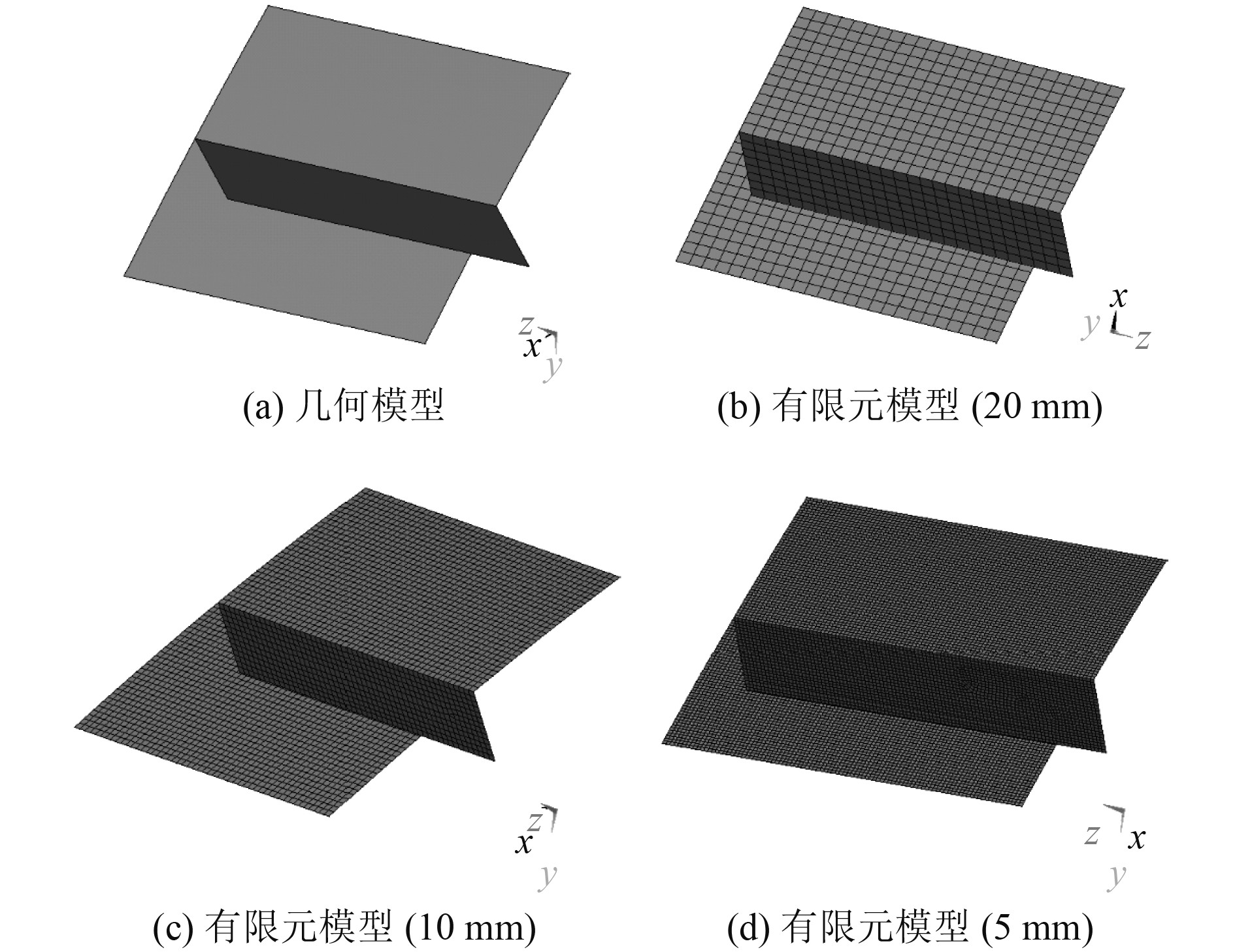
2 基于子模型方法的应力精细化分析为了精细化分析实肋板跨中纵骨根部壳板内表面周向应力,选取含一段纵骨的局部子模型。子模型轴向长度为0.5 m(−1.65~−1.15 m),周向纵骨两侧各0.24 m。分别建立20 mm、10 mm及5 mm网格大小的结构子模型,其位置、几何模型示意图及有限元模型示意图如图4与图5所示。该子模型结构在全局坐标系下的位置、单元类型以及材料参数等均与原整体模型一致。
|
图 4 子模型在整体模型中的位置 Fig. 4 The position of the submodel in the overall model |
|
图 5 子模型几何及有限元模型示意图 Fig. 5 Diagram of submodel geometry and finite element model |
此外还需要对上述子模型的切割边界是否合适进行验证,目前常用的验证方法是对比子模型切割边界上及整体模型中相应位置上的计算结果。如果相应位置的计算结果很接近,则可证明子模型的切割边界合适,反之则需重新确定切割边界的位置来构建新的子模型。
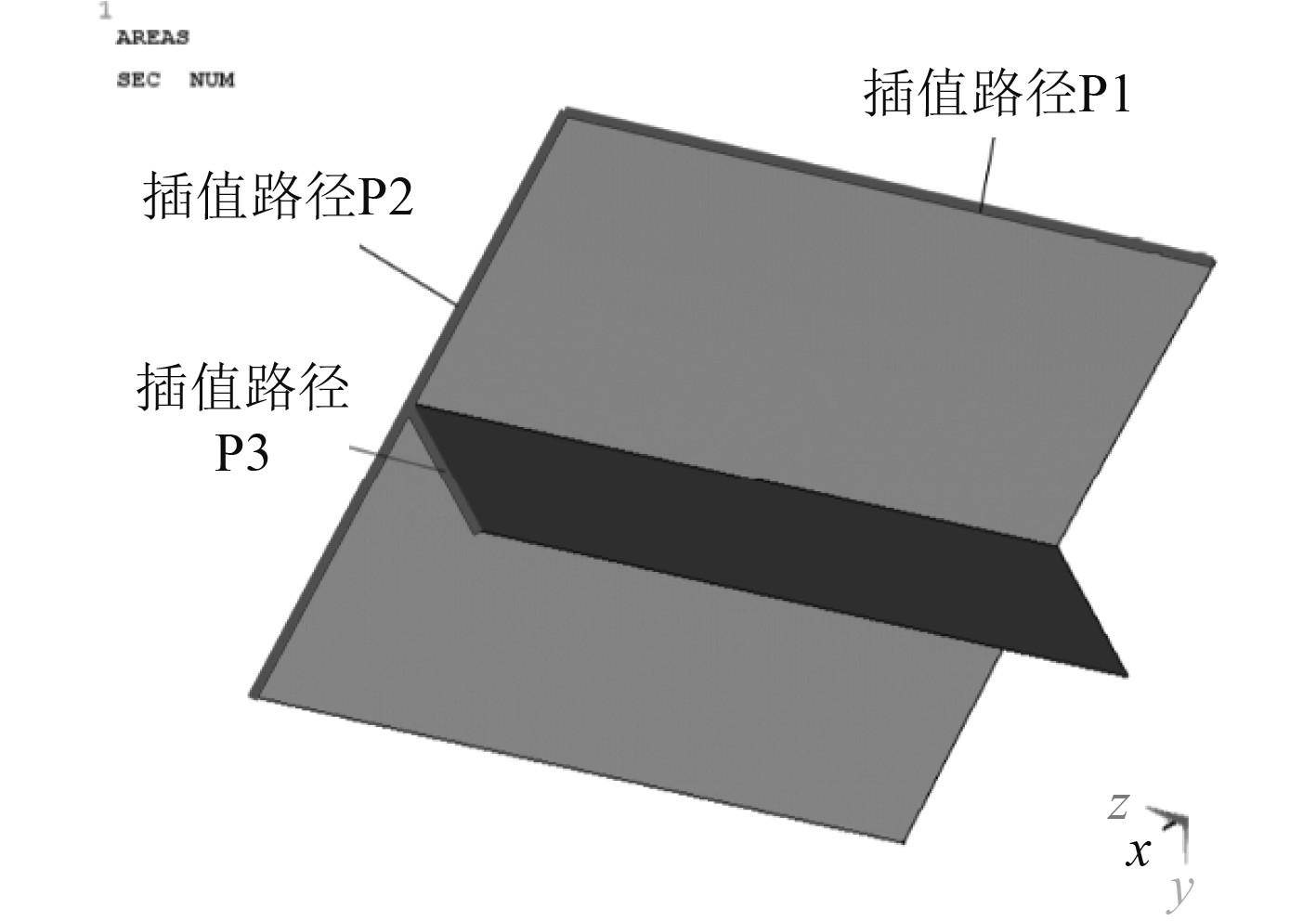
为验证实肋板跨中纵骨根部壳板子模型的切割边界是否合适,按照以上方法选取如图6所示的插值路径并在原整体模型与上述子模型中提取插值路径上对应位置处的Mises应力,其结果如图7所示。图中横坐标表示插值点与路径起始点之间的距离,纵坐标表示插值点处的Mises应力值。
|
图 6 子模型插值路径示意图 Fig. 6 Diagram of submodel interpolation path |
|
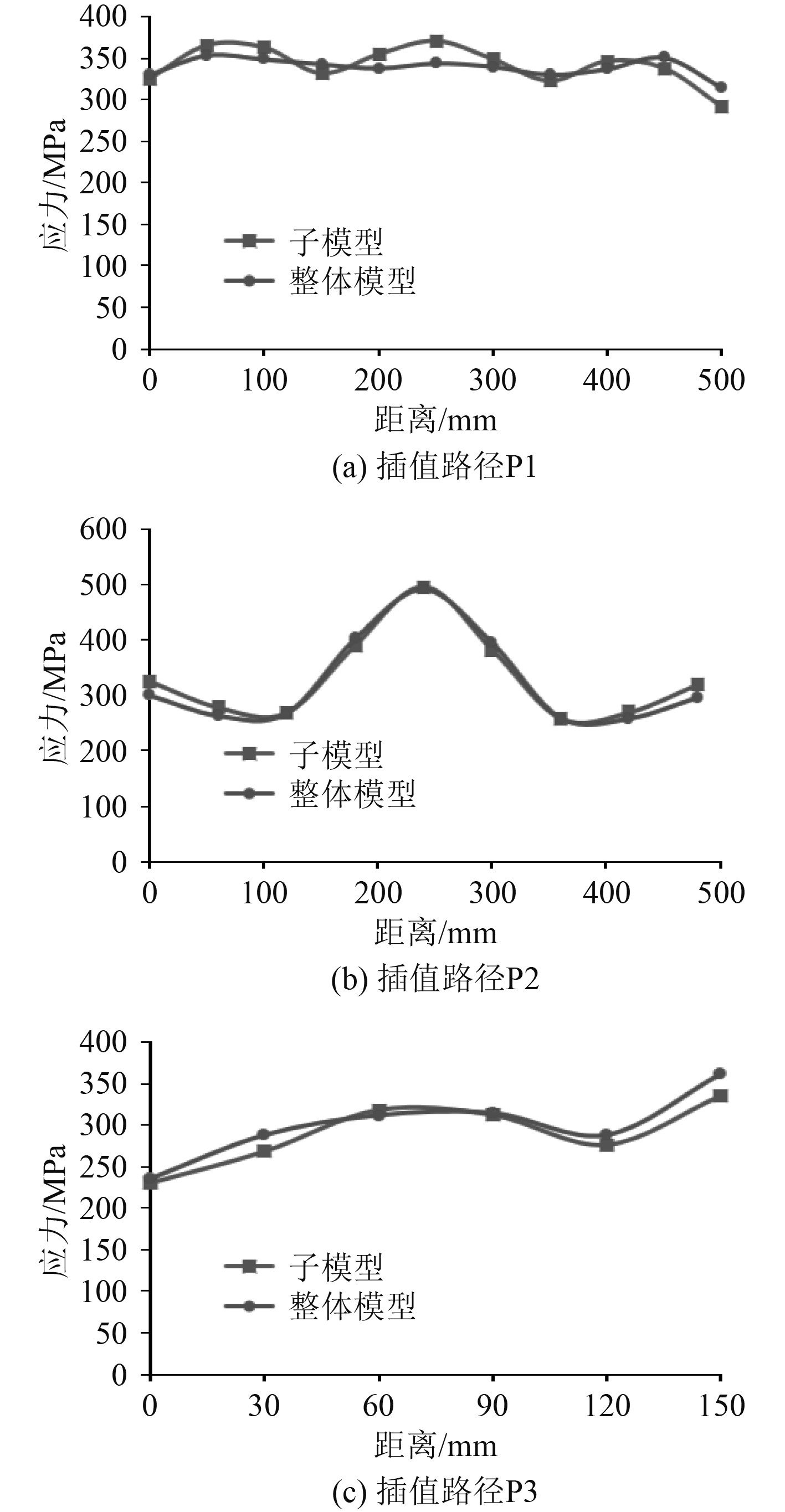
图 7 切割边界路径P1~P3的Mises应力对比图 Fig. 7 Mises stress comparison diagram of cutting boundary path P1~P3 |
由切割边界路径的Mises应力对比图可以看出,子模型与原整体模型在切割边界上的应力大小基本保持一致,因此可以认为子模型的切割边界基本合理。上述子模型的结果如表2所示,实肋板跨中纵骨根部壳板内表面周向应力云图如图8所示。
|
|
表 2 子模型不同网格大小下的计算结果 Tab.2 Calculation results of submodels with different mesh sizes |
|
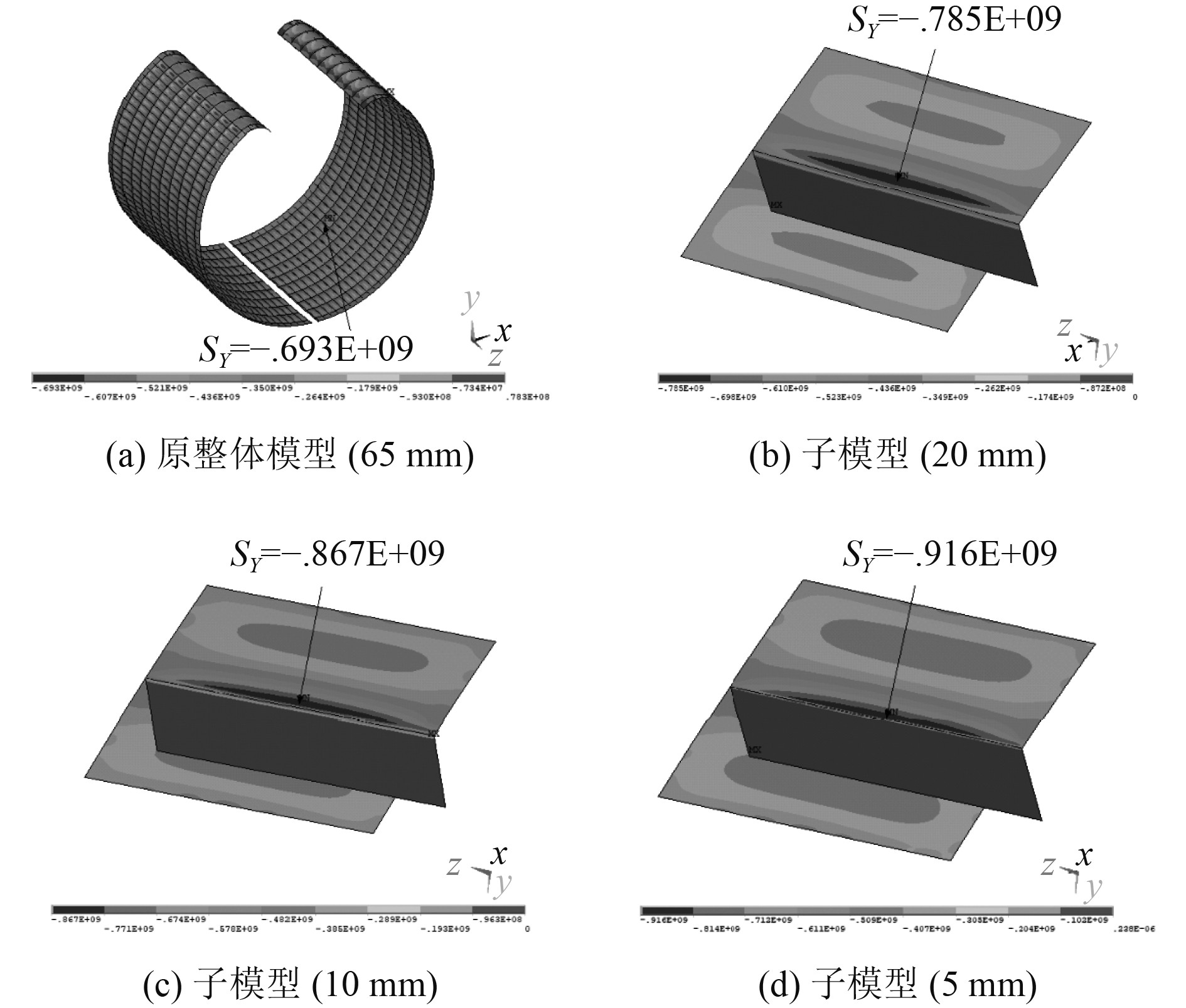
图 8 不同模型及网格大小下的壳板内表面周向应力 Fig. 8 Circumferential stress on inner surface of shell plate with different mesh sizes |
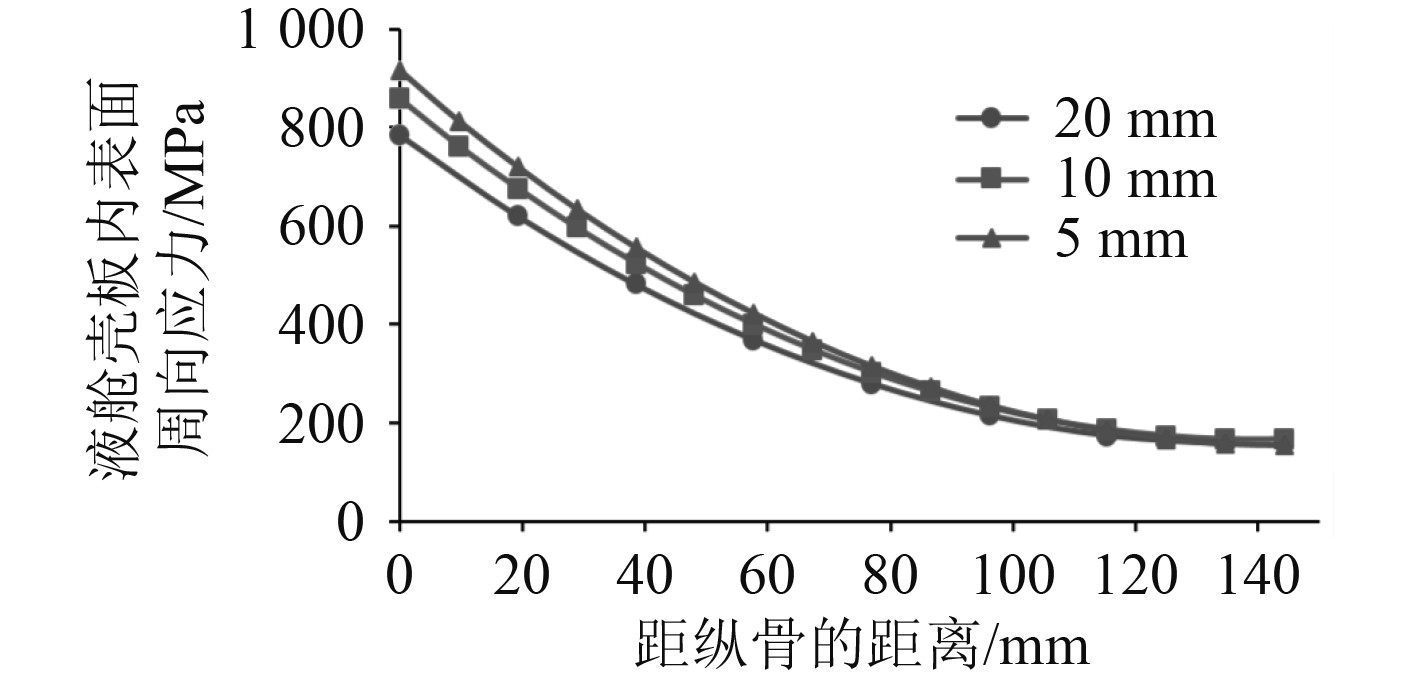
可以看出,实肋板跨中纵骨根部壳板内表面周向应力在网格大小为10 mm时已经收敛,网格再细化对结果影响也不大。子模型中液舱壳板内表面周向应力与距纵骨距离的关系如图9 所示,随着特征点与距纵骨距离的增大,液舱壳板内表面周向应力迅速下降。
|
图 9 壳板内表面周向应力随距纵骨距离的变化曲线图 Fig. 9 Curve of circumferential stress on inner surface of shell plate with distance from longitudinal |
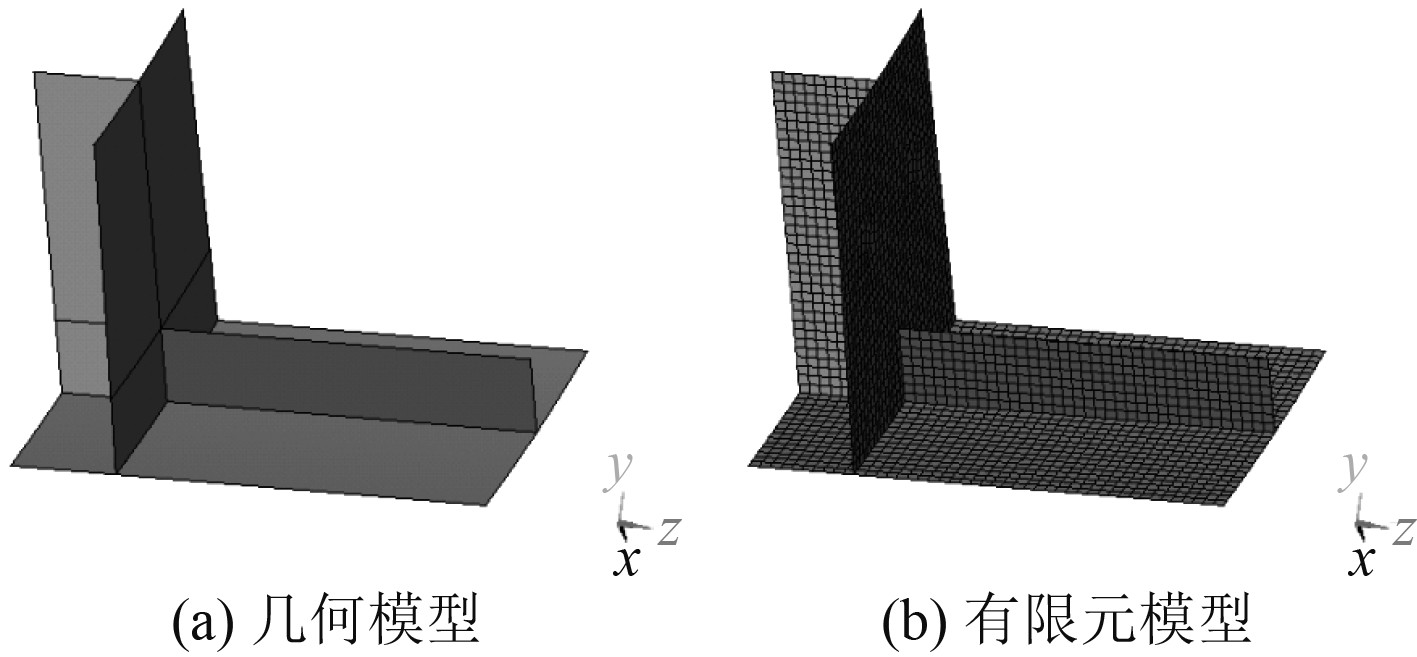
为了精细化分析横舱壁根部纵骨自由翼缘上的总应力,选取含纵骨、横舱壁及横舱壁径向加强筋的局部子模型。子模型轴向长度为0.9 m(−3.35~−2.45 m),周向纵骨两侧各0.3 m,径向长度为0.7 m(4.5~5.2 m)。建立20 mm网格大小的结构子模型,其位置、几何模型示意图及有限元模型示意图如图10与图11所示。该子模型结构在全局坐标系下的位置、单元类型以及材料参数等均与原整体模型一致。

|
图 10 横舱壁处纵骨子模型在整体模型中的位置 Fig. 10 The position of the longitudinal submodel at the transverse bulkhead in the overall model |
|
图 11 横舱壁处纵骨子模型几何及有限元模型示意图 Fig. 11 Diagram of the geometry and finite element model of the longitudinal submodel at the transverse bulkhead |
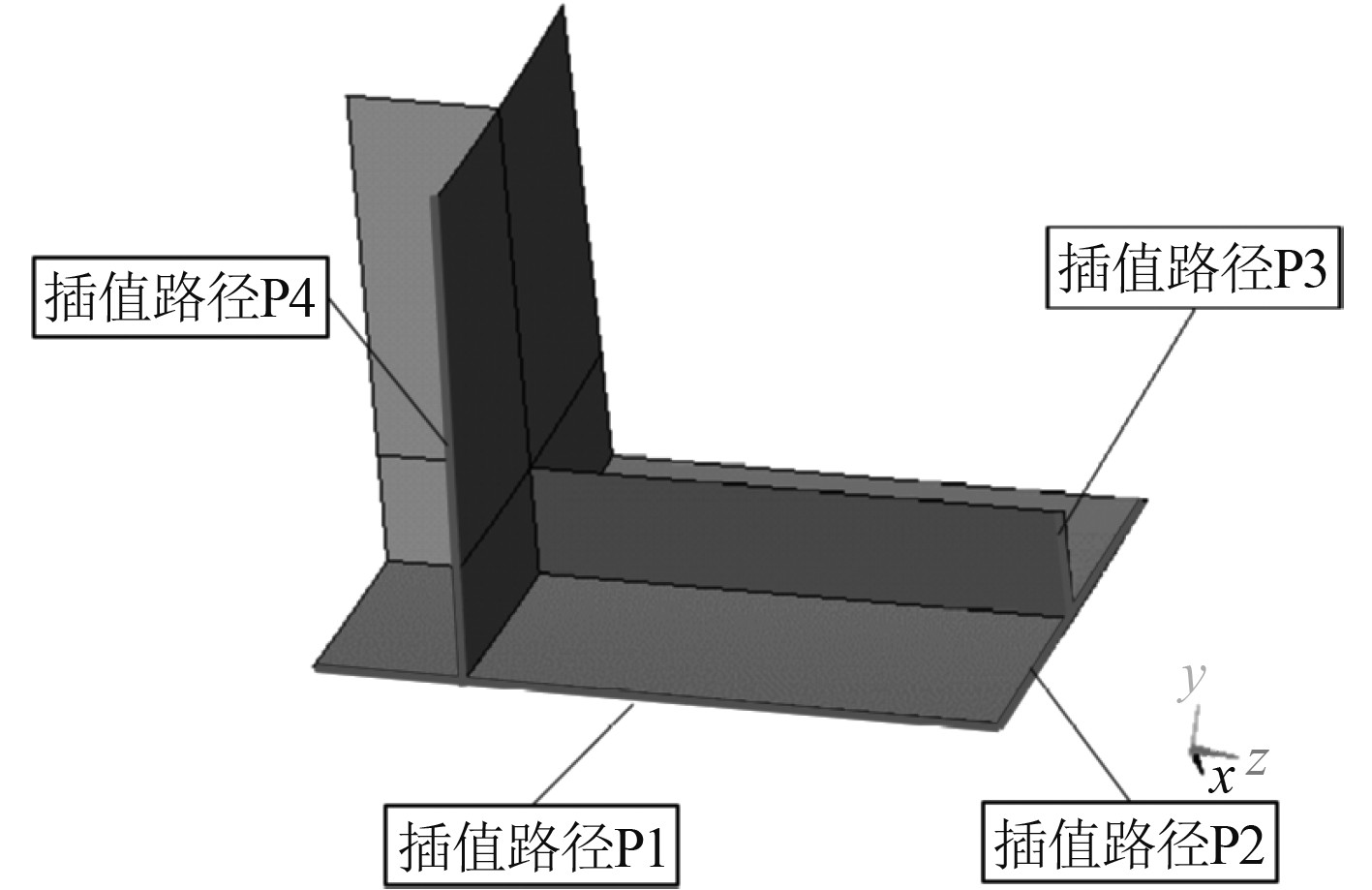
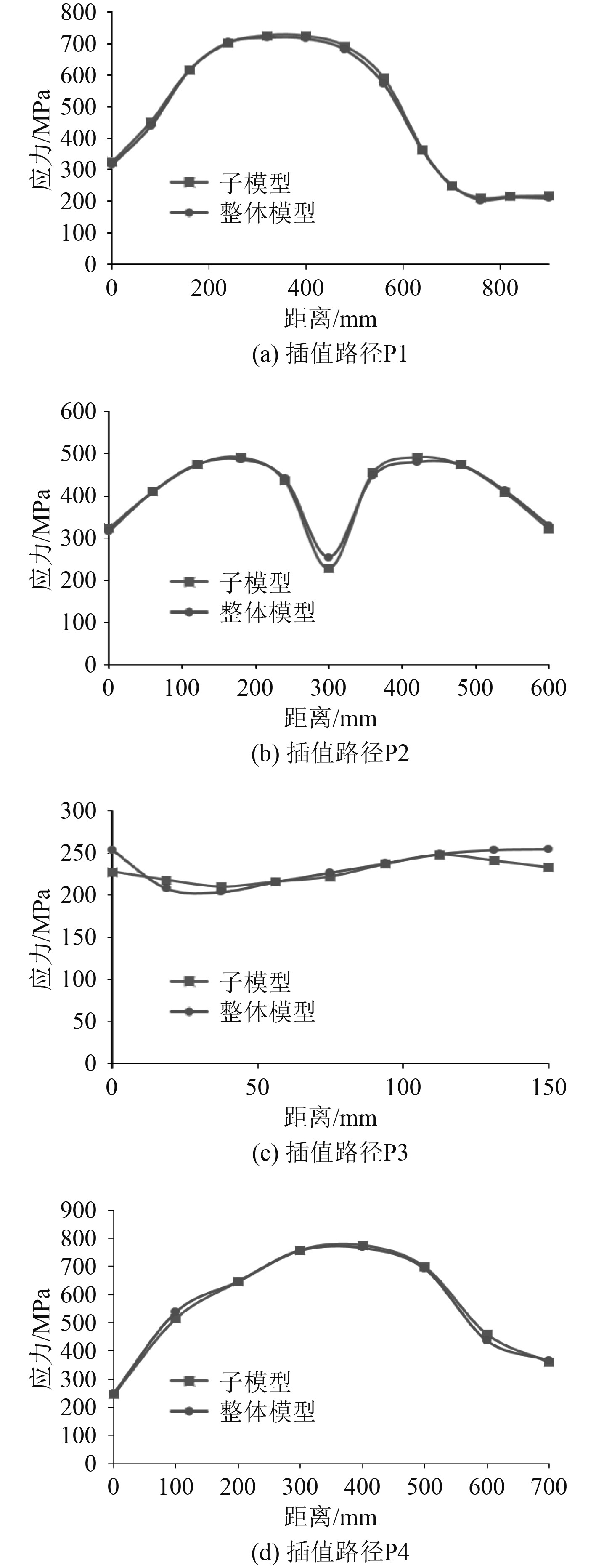
选取如图12所示的插值路径并在原整体模型与上述子模型中提取插值路径上对应位置处的Mises应力,其结果如图13所示。
|
图 12 横舱壁处纵骨子模型插值路径示意图 Fig. 12 Diagram of the interpolation path of the longitudinal submodel at the transverse bulkhead |
|
图 13 横舱壁处纵骨切割边界路径P1~P4的Mises应力对比图 Fig. 13 Mises stress comparison diagram of longitudinal cutting boundary path P1~P4 at transverse bulkhead |
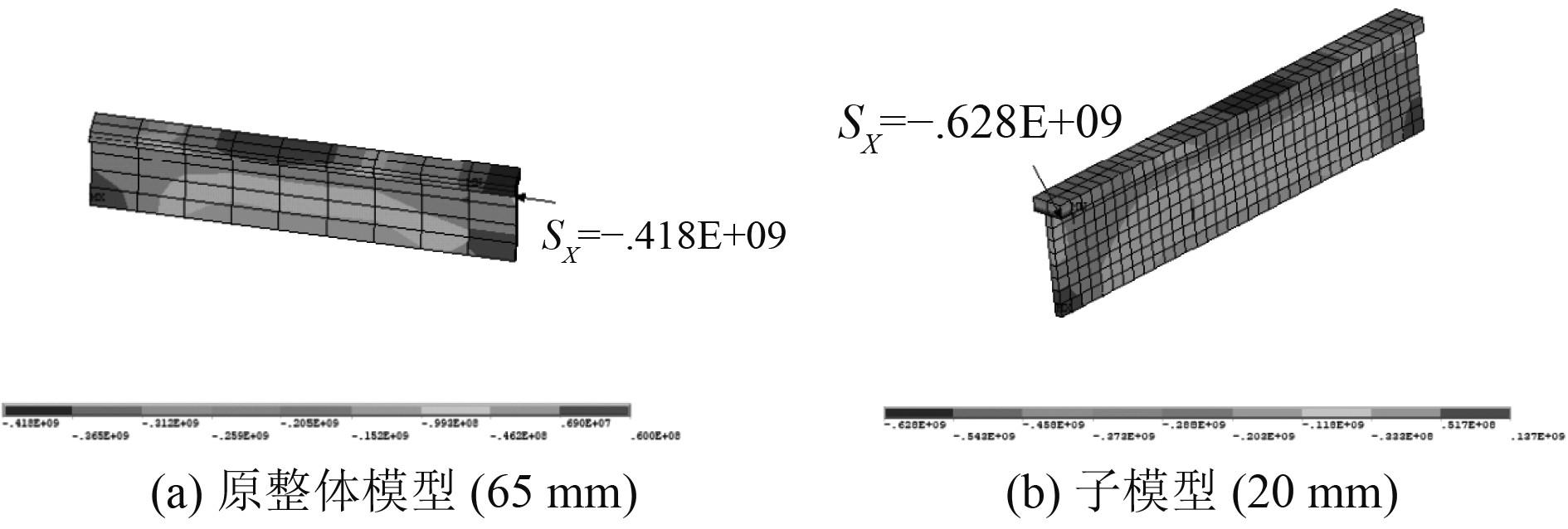
由图13可以看出,横舱壁处纵骨子模型与原整体模型在切割边界上的应力大小基本保持一致,因此可以认为子模型的切割边界合理。上述子模型的计算结果如表3所示,横舱壁根部纵骨自由翼缘上的总应力云图如图14所示。
|
|
表 3 不同模型的计算结果 Tab.3 Calculation results of different models |
|
图 14 不同模型下的横舱壁根部纵骨自由翼缘上的总应力 Fig. 14 Total stress on free flanges of the longitudinals at transverse bulkhead root under different models |
可以看出,随着网格的细化横舱壁根部纵骨自由翼缘上的应力集中状况显著增大,应力有了明显提升。由于端跨纵骨刚度在横舱壁处不连续,且此处横舱壁径向加强筋的弯曲对端跨纵骨变形有影响导致横舱壁根部纵骨自由翼缘处存在明显的局部应力集中情况,通过在横舱壁与纵骨相交处增加肘板的方式来降低此处应力。在上述子模型的基础上考虑如图15所示的肘板,增加肘板后子模型的几何模型示意图及有限元模型示意图如图16所示,计算结果如表4所示,横舱壁根部纵骨自由翼缘上的总应力云图如图17所示。
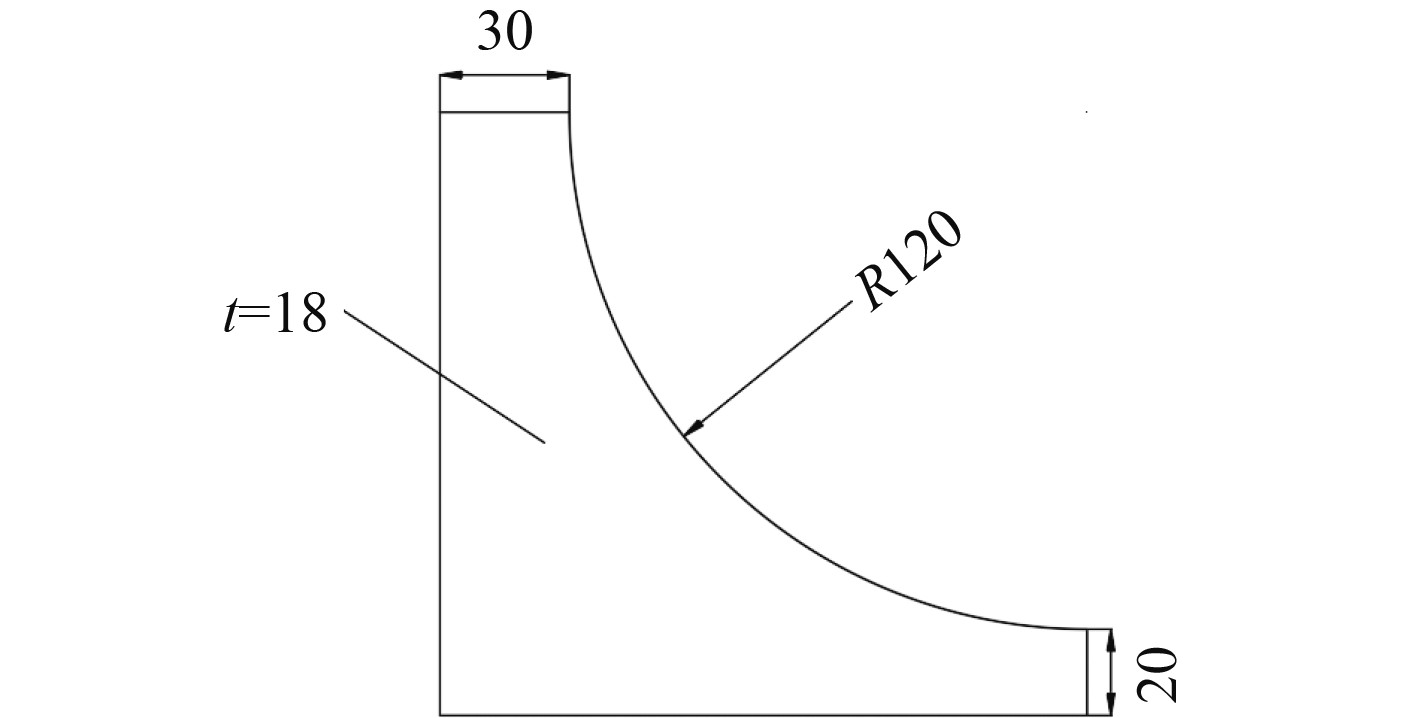
|
图 15 肘板示意图 Fig. 15 Diagram of toggle plate |
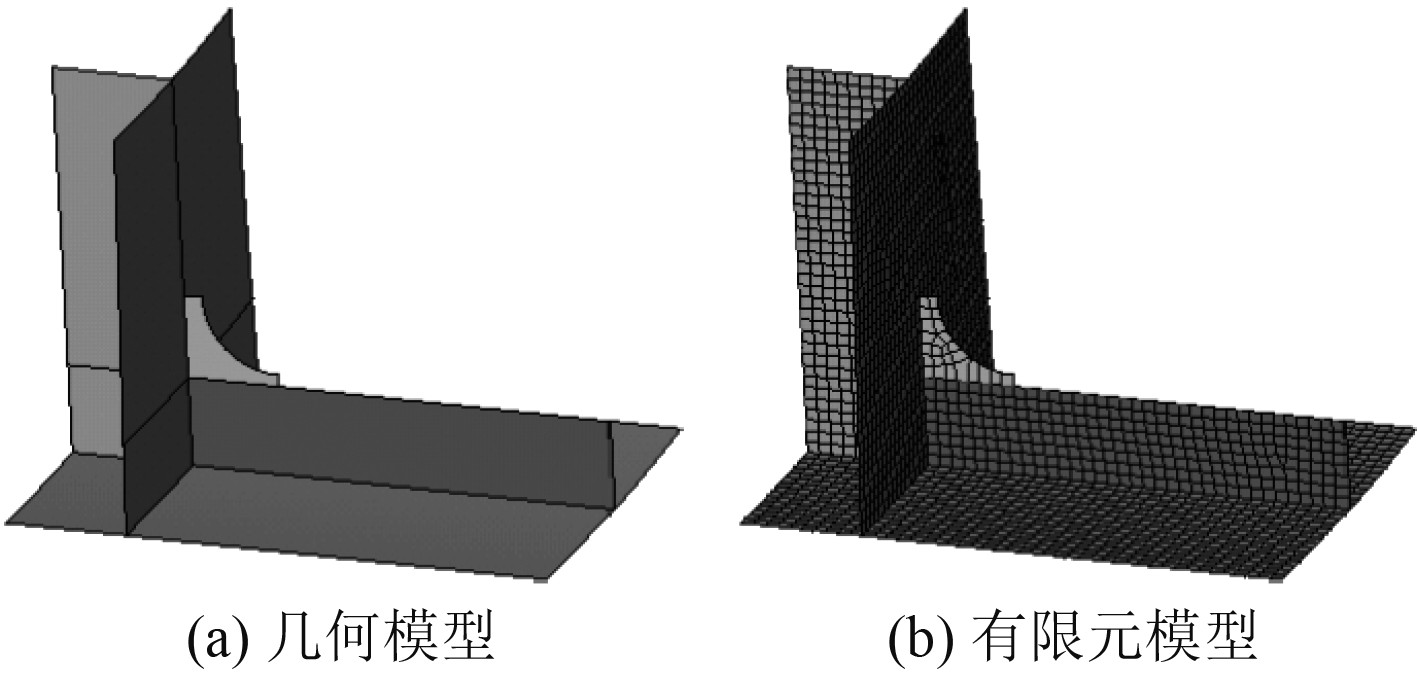
|
图 16 横舱壁处纵骨子模型几何及有限元模型示意图 Fig. 16 Diagram of the geometry and finite element model of the longitudinal submodel at the transverse bulkhead |
|
|
表 4 不同模型的计算结果 Tab.4 Calculation results of different models |
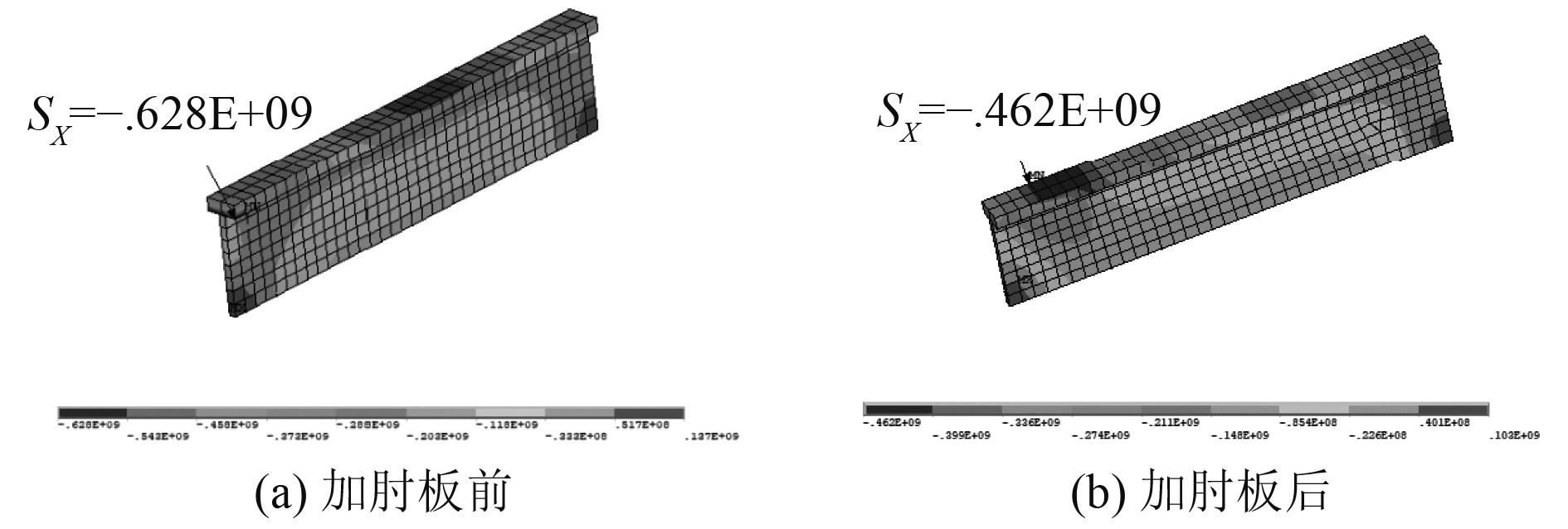
|
图 17 子模型加肘板前后的横舱壁根部纵骨自由翼缘上的总应力 Fig. 17 Total stress on the flanges of longitudinals at the root of transverse bulkheads before and after added with brackets |
可以看出,在纵骨与横舱壁相交处增加肘板后纵骨自由翼缘上的总应力下降了26.43%,而在整体模型横舱壁与纵骨相交处增加肘板后模型总重仅增加了0.118 t。即增加肘板在对整体结构重量影响很小的情况下,取得了较好的效果,说明此方案可行。
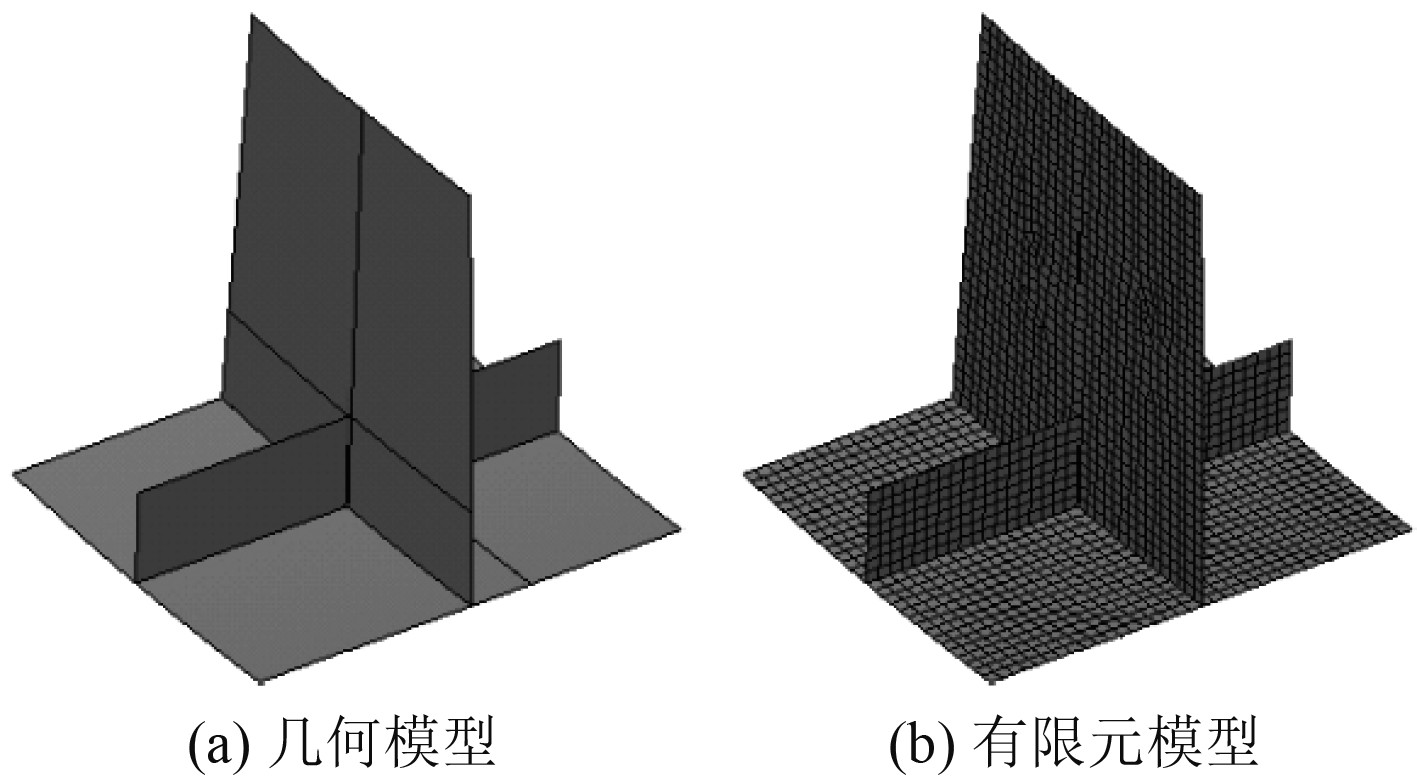
3.2 纵骨与实肋板相交处的变刚度设计为了精细化分析实肋板根部纵骨自由翼缘上的总应力,选取含纵骨及实肋板的局部子模型。子模型轴向长度为0.7 m(−0.7~0 m),周向纵骨两侧各0.3 m,径向长度为0.7 m(4.5~5.2 m)。建立20 mm网格大小的结构子模型,其位置、几何模型示意图及有限元模型示意图如图18与图19所示。该子模型结构在全局坐标系下的位置、单元类型以及材料参数等均与原整体模型一致。
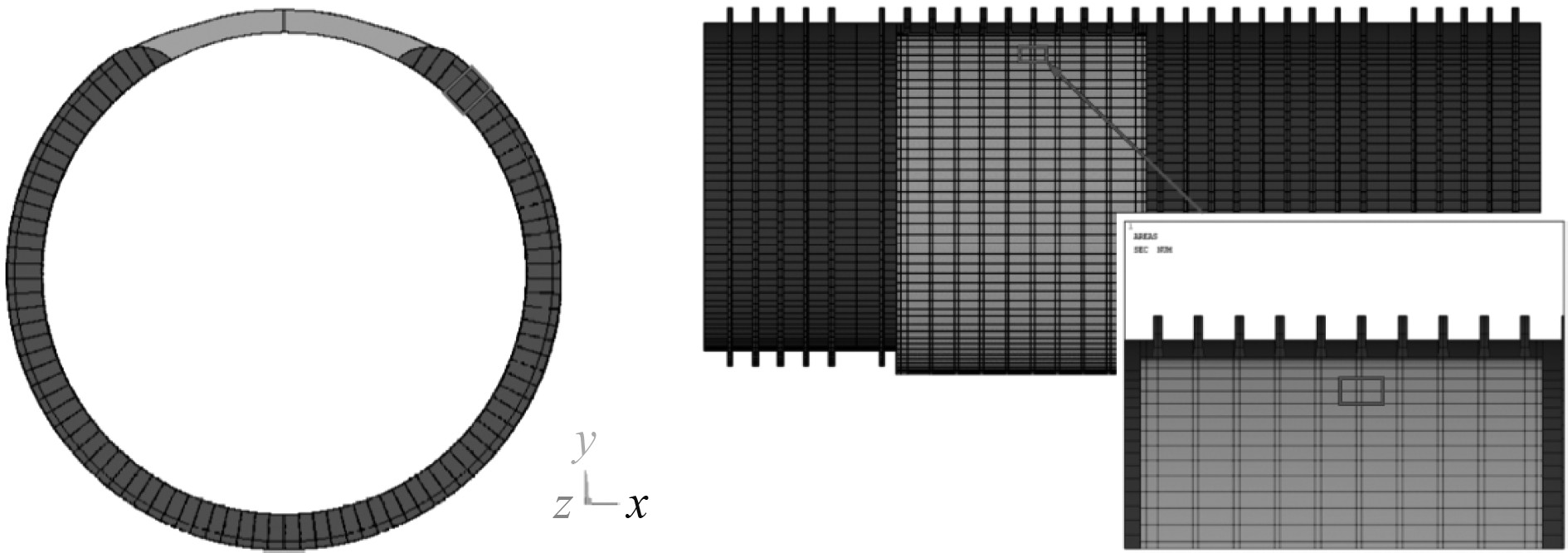
|
图 18 实肋板处纵骨子模型在整体模型中的位置 Fig. 18 The position of the longitudinal submodel at the solid floor in the overall model |
|
图 19 实肋板处纵骨子模型几何及有限元模型示意图 Fig. 19 Diagram of the geometry and finite element model of the longitudinal submodel at the solid floor |
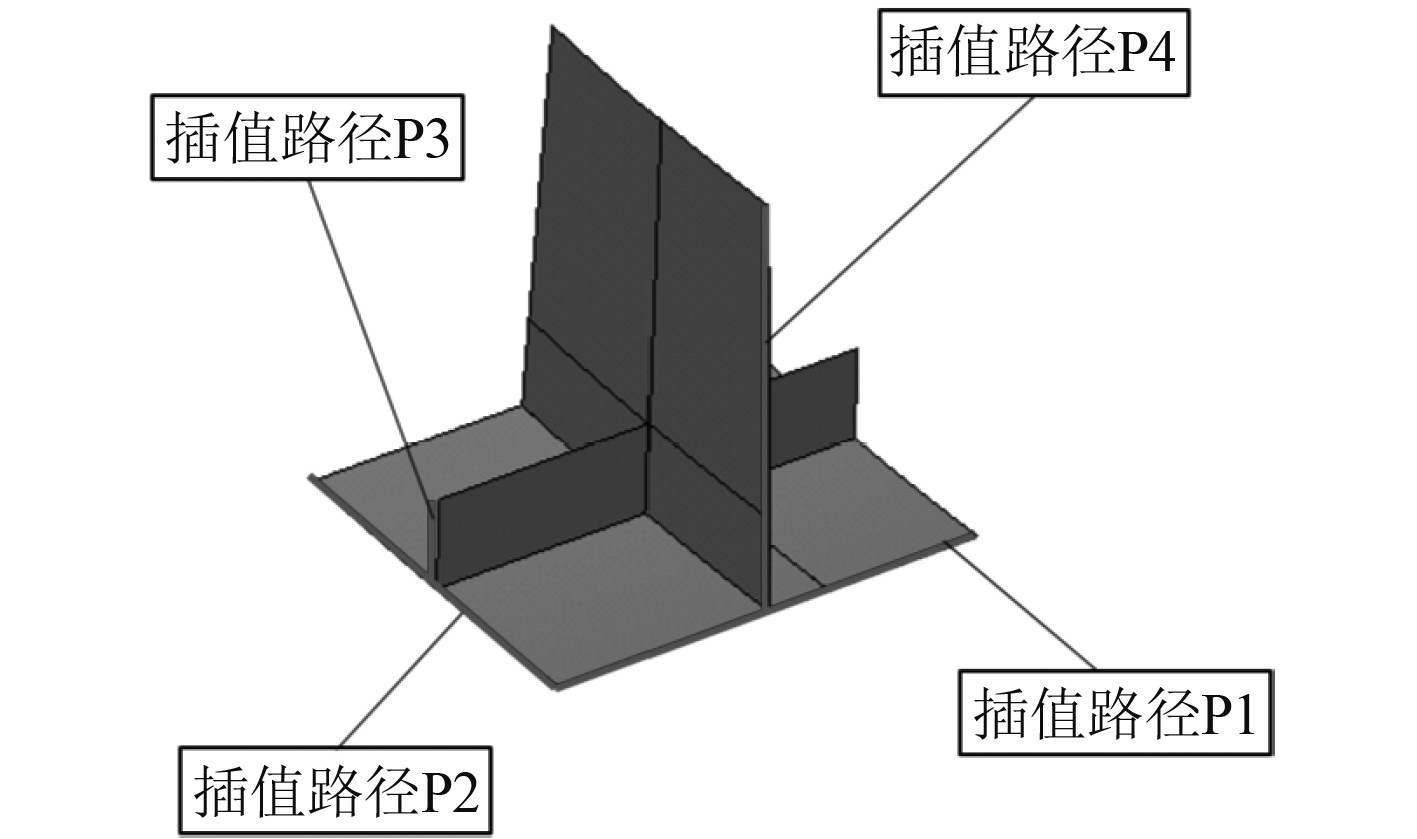
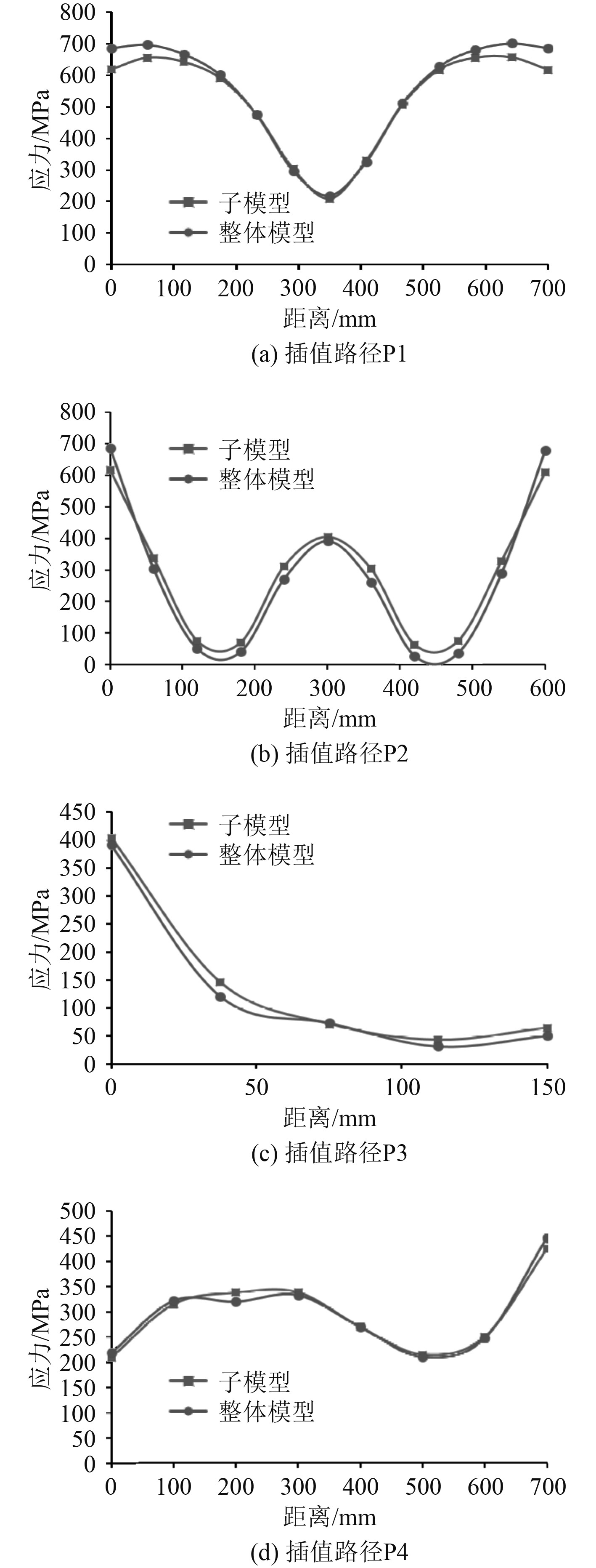
选取如图20所示的插值路径并在原整体模型与上述子模型中提取插值路径上对应位置处的Mises应力,其结果如图21所示。
|
图 20 实肋板处纵骨子模型插值路径示意图 Fig. 20 Diagram of the interpolation path of the longitudinal submodel at the solid floor |
|
图 21 实肋板处纵骨切割边界路径P1~P4的Mises应力对比图 Fig. 21 Mises stress comparison diagram of longitudinal cutting boundary path P1~P4 at the solid floor |
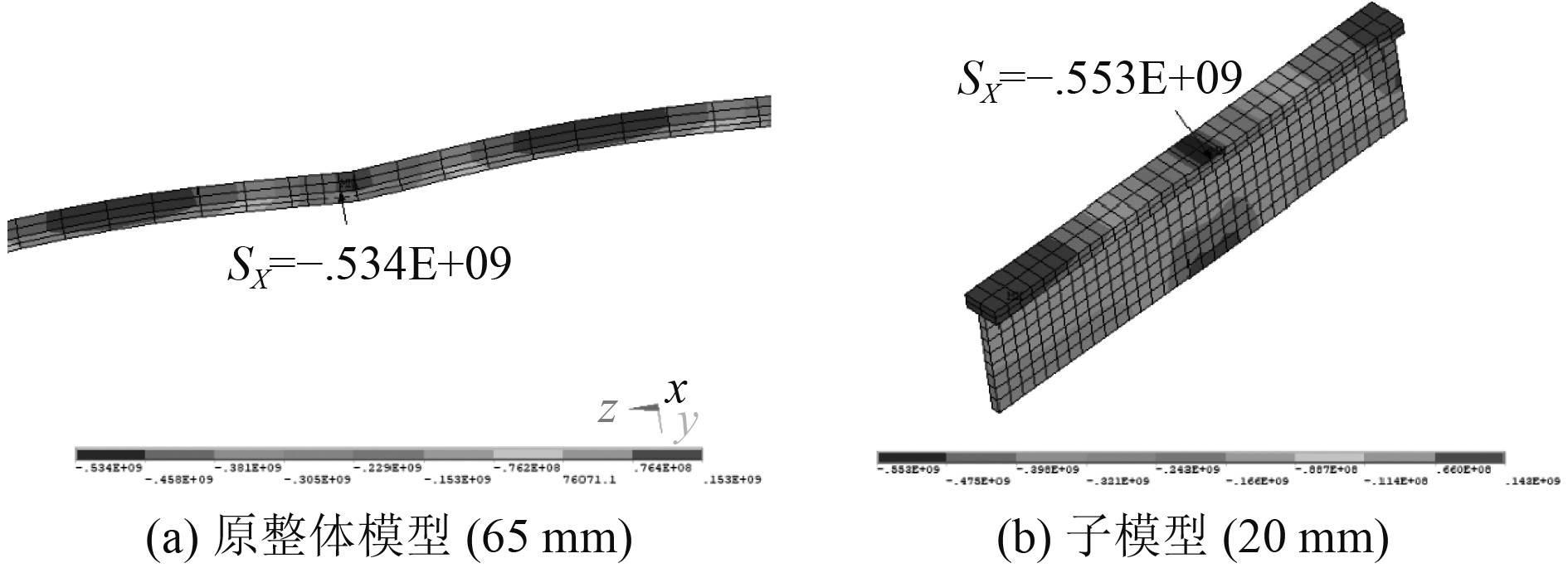
可以看出,子模型与原整体模型在切割边界上的应力大小基本保持一致,因此可以认为子模型的切割边界基本合理。上述子模型的计算结果如表5所示,实肋板根部纵骨自由翼缘上的总应力云图如图22所示。
|
|
表 5 不同模型的计算结果 Tab.5 Calculation results of different models |
|
图 22 不同模型下的实肋板根部纵骨自由翼缘上的总应力 Fig. 22 Total stress on free flanges of the longitudinals at solid floor root under different models |
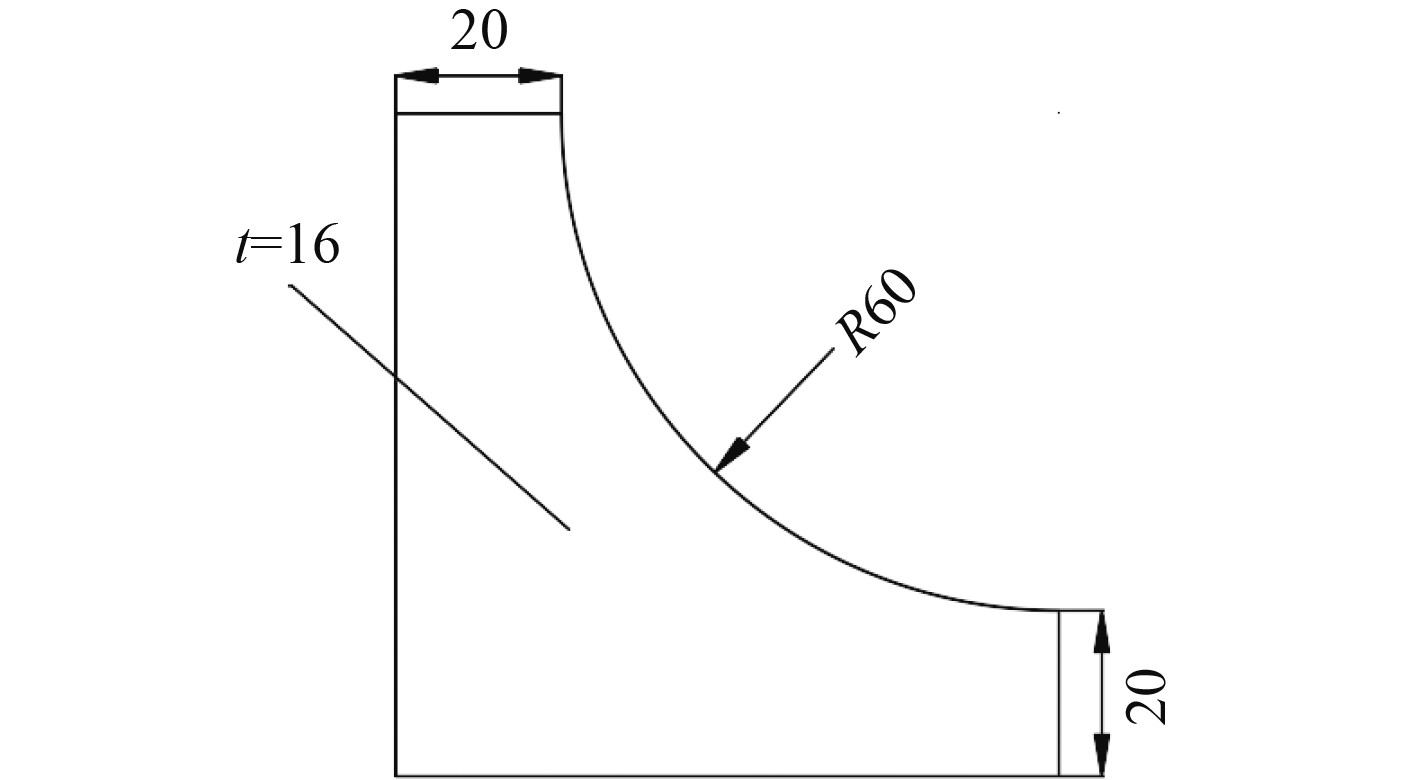
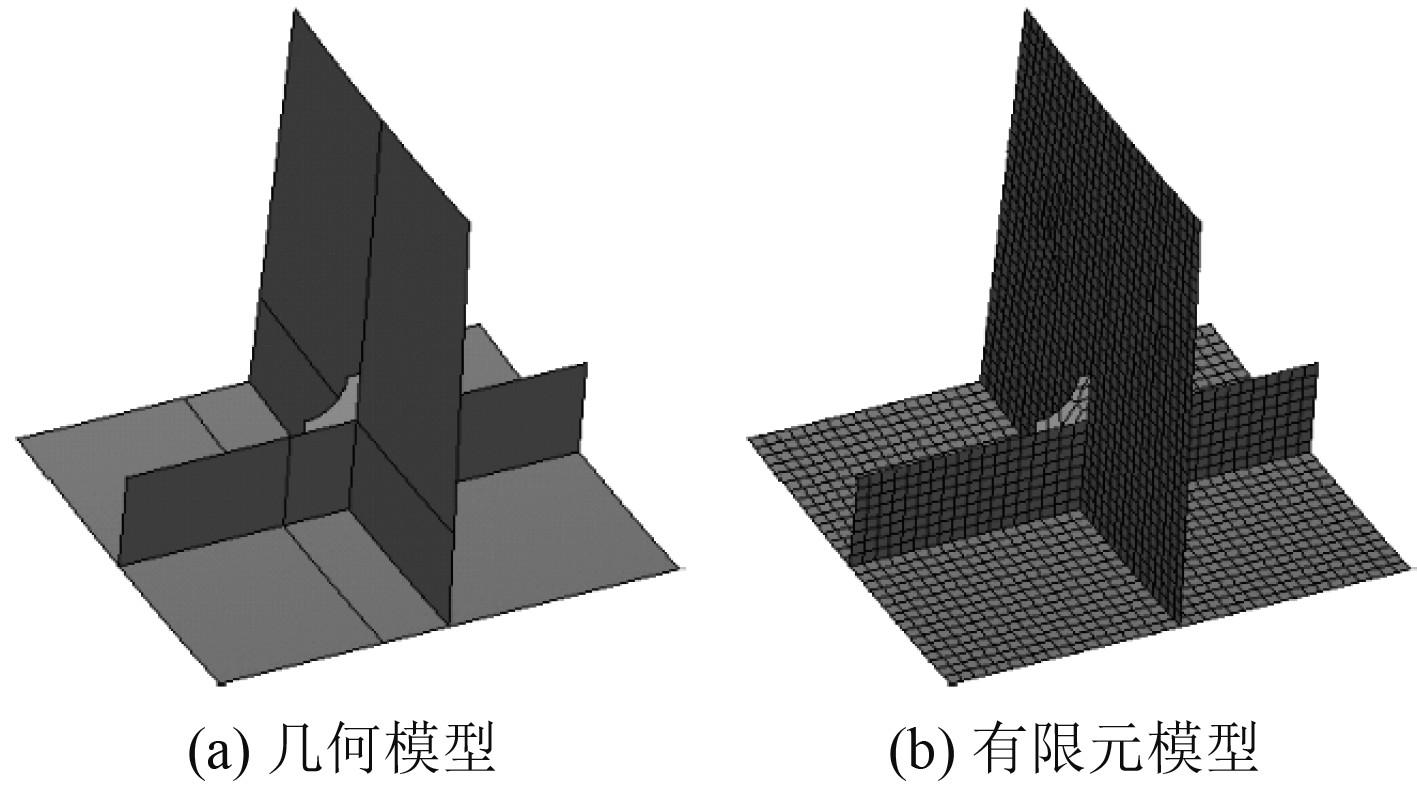
可以看出,由于原整体模型中实肋板根部纵骨网格已局部加密至25 mm,故原整体模型与子模型计算结果较为接近。由于实肋板对中跨纵骨有较强的支撑及约束作用,故实肋板根部纵骨自由翼缘处存在明显的局部应力集中情况,通过在实肋板与纵骨相交处的轴向两侧增加肘板的方式来降低此处应力。在上述子模型的基础上考虑如图23所示的肘板,增加肘板后子模型的几何模型示意图及有限元模型示意图如图24所示,计算结果如表6所示,实肋板根部纵骨自由翼缘上的总应力云图如图25所示。
|
图 23 肘板示意图 Fig. 23 Diagram of toggle plate |
|
图 24 实肋板处纵骨子模型几何及有限元模型示意图 Fig. 24 Diagram of the geometry and finite element model of the longitudinal submodel at the solid floor |
|
|
表 6 不同模型的计算结果 Tab.6 Calculation results of different models |
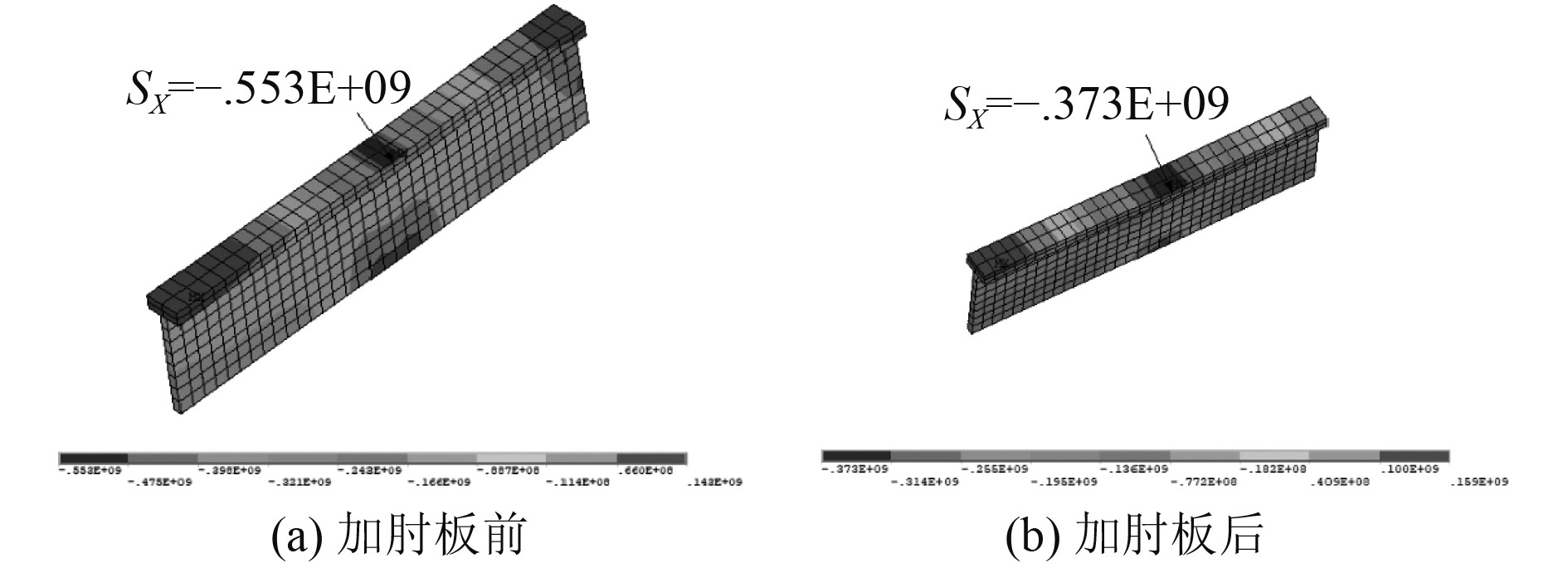
|
图 25 子模型加肘板前后的实肋板根部纵骨自由翼缘上的总应力 Fig. 25 Total stress on the flanges of longitudinals at the root of solid floor before and after added with brackets |
可以看出,在实肋板与纵骨相交处增加肘板后纵骨自由翼缘上的总应力下降了32.55%,而在整体模型实肋板与纵骨相交处增加肘板后整体结构总重仅增加了0.153 t。即增加肘板在对整体结构重量影响很小的情况下,取得了较好的效果,说明此方案可行。
4 结 语本文对耐压液舱结构方案进行力学特性分析后,对规范与有限元结果差异较大的特征应力进行精细化分析,给出了合理解释,并对实肋板根部纵骨自由翼缘上的总应力进行讨论,最后得出以下结论:
1)纵骨根部液舱壳板内表面周向应力的规范结果为−831.77 MPa,整体模型的有限元结果为−693 MPa,二者相差20.02%。对上述部位采用子模型方法进行局部高应力的精细化分析后,有限元子模型的结果为−867 MPa,与规范结果相差4.06%,并发现随着距纵骨周向距离的增大液舱壳板内表面周向应力迅速下降。
2)经有限元计算发现纵骨自由翼缘上的总应力在实肋板根部与横舱壁根部有较大不同,即有限元计算中可体现不同轴向位置纵骨之间的差别。而规范中的实肋板根部纵骨自由翼缘上的总应力无法体现上述不同部位的差别,故在校核结果时应增加横舱壁根部纵骨自由翼缘上的总应力这一特征量。
3)由于端跨纵骨刚度在横舱壁处不连续,且横舱壁径向加强筋的弯曲对端跨纵骨变形有影响导致横舱壁根部纵骨自由翼缘处存在明显的局部应力集中情况。本文通过在纵骨与横舱壁相交处增加肘板的方式来降低此处应力。横舱壁根部纵骨自由翼缘上的总应力在原整体模型中的有限元结果为−418 MPa,子模型中的有限元结果为−628 MPa,增加肘板后子模型中的有限元结果为−462 MPa,降低了26.43%。
4)由于实肋板对中跨纵骨有较强的支撑及约束作用,故实肋板根部纵骨自由翼缘处存在明显的局部应力集中情况。本文通过在纵骨与实肋板相交处的轴向两侧增加肘板的方式来降低此处应力。实肋板根部纵骨自由翼缘上的总应力在原整体模型中的有限元结果为−534 MPa,子模型中的有限元结果为−553 MPa,增加肘板后有限元子模型中的结果为−373 MPa,降低了32.55%。纵骨变刚度设计是重量成本较低的降低纵骨自由翼缘总应力的可选方案。
| [1] |
张胜民. 基于有限元软件Ansys 7.0的结构分析[M]. 北京: 清华大学出版社, 2004: 196–204.
|
| [2] |
GAO Y H. Application of sub-model technique in stress analysis and structure optimization of the supporting region of large spherical tank[J]. Journal of Mechanical Strength, 2010, 32(5): 735-739. |
| [3] |
夏伟, 胡成, 瞿尔仁. Ansys子模型分析技术在处理应力集中时的应用[J]. 工程与建设, 2006 (2): 92–94.
|
| [4] |
高耀东, 杨建鸣, 汪建新. Ansys子模型技术的应用[J]. 包头钢铁学院学报, 2002 (4): 340–342.
|
| [5] |
AN X, LI L, LIU X. Strength analysis of threads on special container based on finite element sub-model method[J]. Journal of Mechanical Strength, 2013, 35(6): 816-822. |
| [6] |
苏罗青, 卢龙文, 乔欢欢. 基于子模型技术的某船贯穿式大开口角隅的结构优化分析[J]. 广东造船, 2020, 39(4): 26–30.
|
| [7] |
郭磊磊, 包家汉, 王勇. 基于子模型法的大型薄壁结构有限元分析[J]. 机械设计与研究, 2013, 29(4): 57–60.
|
| [8] |
张志兴, 邓长根, 巩俊松. 基于子模型法的钢拱桥关键梁段精细化分析[J]. 科学技术与工程, 2021, 21(20): 8656–8662.
|
| [9] |
孙倩, 廖建彬, 蔡振雄. 潜艇耐压液舱区域有限元应力计算[J]. 船海工程, 2007 (2): 17–20.
|
| [10] |
李坤宏, 陈峥. 有限元分析在船舶复杂结构强度计算与优化中的应用[J]. 舰船科学技术, 2020, 42(20): 4-6. LI K H, CHEN Z. Application of finite element analysis in strength calculation and optimization of complex hull structure[J]. Ship Science and Technology, 2020, 42(20): 4-6. |
 2023, Vol. 45
2023, Vol. 45
