0 引　言

船舶利用航行动力定位系统，控制船舶在预期航线上航行。航行动力定位系统无需锚泊系统，通过控制推进装置，改善船舶航行过程中受到的风、浪等扰动^[1]，保持船舶以固定姿态，精准跟踪船舶航行的预期轨迹，满足船舶的航行精度需求^[2]。船舶航行动力系统具有操作简便、定位精度高、机动性强的优点，对海床无破坏，广泛应用于不同类型的船舶中。为了提升船舶航行动力定位系统的定位精度^[3]，以及船舶航行过程中的操纵性能，船舶航行动力系统需要一个全面而精准的数学模型。针对船舶航行动力定位系统构建数学模型，模型的参数识别结果，对于提升系统的运行性能影响显著^[4]。

目前已有众多学者针对船舶运动的参数识别进行研究。祝添权等^[5]将支持向量机方法应用于船舶操纵响应模型参数识别中，该方法针对船舶运行状态，构建了二阶非线性响应模型。选取最小二乘支持向量机识别模型参数。该方法有效识别船舶操作响应模型参数，提升船舶的操纵性能，快速将定位结果切换至下一个路径点的坐标。梅斌等^[6]构建了船舶操纵运动灰箱模型，设置船舶运动数学模型作为灰箱模型的备选模型，确定备选模型与待识别参数之间的相关系数，选取相似准则将观测数值映射至备选模型的输入值域中，利用线性支持向量回归机作为参数误差补偿方法，通过全局优化算法，调节线性支持向量回归机的边界参数，获取最终的参数识别结果。该方法可以满足小舵角情况下的参数识别要求。以上方法虽然均可以实现船舶操作系统的参数识别，但是存在识别过程过于复杂，影响参数识别实时性的缺陷。针对以上研究在参数识别中存在的问题，设计基于船舶航行定位参数识别的非线性运动方程。针对船舶航行动力定位系统，构建参数识别的数学模型，选取粒子群优化算法，对参数识别模型进行优化，提升船舶航行定位参数识别精度，为船舶航行提供保障。

1 船舶航行定位参数识别 1.1 船舶航行动力定位系统的非线性运动方程

船舶航行时的海况较为复杂，通过船舶航行动力定位系统，控制船舶的横荡、纵荡和首摇的水平面3个自由度运动。为了精准描述船舶航行在水平面上的运动，构建大地坐标系 $ {X_E}O{Y_E} $ 和随船坐标系 $ XOY $ 2个坐标系。利用2个坐标系的转换，估算船舶位置、船舶速度以及船舶航行所需的控制力。 $ \phi $ 与 $ r $ 分别为大地坐标系的首摇角和船舶位置， $ \eta = {\left[ {x,y,\phi } \right]^{\rm{T}}} $ 为船舶的位置向量。 $ \upsilon = {\left[ {u,v,r} \right]^{\rm{T}}} $ 为随船坐标系下的速度向量，其中 $ v $ 、 $ u $ 与 $ r $ 分别表示船舶横荡速度、纵荡速度以及首摇角速度。2个坐标系的转换矩阵表达式如下:

$ \dot \eta = {\boldsymbol{R}}\left( \phi \right)\upsilon，$

(1)

式中， $ {\boldsymbol{R}} $ 为旋转矩阵，其表达式如下：

$ R\left( \phi \right) = \left[ {\begin{array}{*{20}{c}} {\cos \phi }&{ - \sin \phi }&0 \\ {\sin \phi }&{ - \cos \phi }&0 \\ 0&0&1 \end{array}} \right] 。$

(2)

依据船舶航行动力定位系统的特性，利用船舶操纵性理论，构建船舶航行动力定位系统的非线性运动方程如下：

$ \begin{gathered} {\boldsymbol{M}}\dot \upsilon + {{\boldsymbol{C}}_R}\upsilon + {{\boldsymbol{C}}_A}\upsilon + {{\boldsymbol{D}}_L}\upsilon + {V_R}\left( {{\upsilon _r},\gamma } \right)= \\ {\tau _1} + {\tau _2} + {\tau _3}。\\ \end{gathered} $

(3)

式中： $ {\boldsymbol{M}} $ 与 $ {D_L} $ 分别为船舶惯性矩阵以及线性水动力阻尼矩阵； $ {C_R} $ 与 $ {C_A} $ 分别为船舶刚体以及船舶附加质量的离心力矩阵； $ {\tau _1} $ 与 $ {\tau _2} $ 分别为船舶航行的波浪力矩阵以及风力矩阵； $ {\tau _3} $ 与 $ \gamma $ 分别为船舶推进器的控制矩阵以及风舷角； $ {V_R} $ 为相对风速。

1.2 基于无迹卡尔曼滤波的参数识别数学模型

利用无迹卡尔曼滤波方法，构建船舶航行定位系统参数识别的数学模型。船舶航行定位系统参数识别的数学模型构建过程如下：

1）初始化

对无迹卡尔曼滤波进行初始化：

$ \left\{ {\begin{array}{*{20}{c}} {{{\hat w}_0} = E\left( {{w_0}} \right)} ，\\ {{P_0} = E \geqslant \left( {\left( {{w_0} - {{\hat w}_0}} \right){{\left( {{w_0} - {{\hat w}_0}} \right)}^{\rm{T}}}} \right)} 。\end{array}} \right. $

(4)

式中： $ {w_0} $ 与 $ {\hat w_0} $ 分别为船舶航行定位系统的初始状态向量以及初始状态向量估计； $ E\left( {} \right) $ 与 $ {P_0} $ 分别为数学期望以及初始状态误差的协方差矩阵。

2）计算船舶航行定位采样点及其权值

船舶航行定位采样点的计算公式如下：

$ {\chi _{k - 1}} = \left[ {{{\hat w}_{k - 1}},{{\hat w}_{k - 1}} + \sqrt {n\beta {P_{k - 1}}} ,{{\hat w}_{k - 1}} - \sqrt {n\beta {P_{k - 1}}} } \right]，$

(5)

权值系数计算公式如下：

$ {\varphi _{0m}} = \frac{\beta }{{n + \beta }} ，$

(6)

$ {\varphi _{0c}} = \frac{\beta }{{n + \beta }} + \left( {1 - {\varepsilon ^2} + \xi } \right) ，$

(7)

$ {\varphi _{im}} = {\varphi _{ic}} = \frac{\beta }{{2\left( {n + \beta } \right)}}。$

(8)

式中： $ {\varphi _{im}} $ 与 $ {\varphi _{ic}} $ 分别为船舶航行定位采样点的一阶与二阶统计特性加权系数； $ n $ 与 $ \varepsilon $ 分别为船舶航行定位参数状态向量的维度以及采样点的分散程度； $ \beta $ 与 $ \xi $ 分别为比例因子以及常数。

3）船舶航行定位采样点更新

船舶航行定位参数的状态预测均值为：

$ {\hat w_{k\left| {k - 1} \right.}} = \sum\limits_{i = 0}^{2n} {{\varphi _{im}}{\chi _{k - 1}}}，$

(9)

船舶航行定位参数的协方差矩阵表达式如下：

$ {P_{k\left| {k - 1} \right.}} = \sum\limits_{i = 0}^{2n} {{\varphi _{ic}}\left( {{\chi _{k - 1}} - {{\hat w}_{k\left| {k - 1} \right.}}} \right)} {\left( {{\chi _{k - 1}} - {{\hat w}_{k\left| {k - 1} \right.}}} \right)^{\rm{T}}}，$

(10)

利用 $ {\hat w_{k\left| {k - 1} \right.}} $ 与 $ {P_{k\left| {k - 1} \right.}} $ 更新采样点的计算公式为：

$ \begin{split} {\chi _{k\left| {k - 1} \right.}} = &\left[ {{{\hat w}_{k\left| {k - 1} \right.}},} \right.{{\hat w}_{k\left| {k - 1} \right.}} + \\ & \left. {\sqrt {\left( {n + \beta } \right){P_{k\left| {k - 1} \right.}}} ,{{\hat w}_{k\left| {k - 1} \right.}} - \sqrt {\left( {n + \beta } \right){P_{k\left| {k - 1} \right.}}} } \right] 。\end{split} $

(11)

4）确定协方差矩阵

船舶航行定位参数状态的测量均值表达式为：

$ {\hat y_k} = \sum\limits_{i = 0}^{2n} {{\varphi _{im}}\left[ {\chi _{i,k\left| {k - 1} \right.}^{\rm{T}}X\left( k \right) - \left( {\chi _{i,k\left| {k - 1} \right.}^{\rm{T}}X\left( {k - 1} \right)} \right)} \right]} $

(12)

测量均值的协方差矩阵表达式如下：

$ \begin{split} {P_y} = &\sum\limits_{i = 0}^{2n} {{\varphi _{ic}}} \left( {\chi _{i,k\left| {k - 1} \right.}^{\rm{T}}X\left( k \right) - \left( {\chi _{i,k\left| {k - 1} \right.}^{\rm{T}}X\left( {k - 1} \right)} \right)} \right)\times \\ &{\left( {\chi _{i,k\left| {k - 1} \right.}^{\rm{T}}X\left( k \right) - \left( {\chi _{i,k\left| {k - 1} \right.}^{\rm{T}}X\left( {k - 1} \right)} \right) - {{\hat y}_k}} \right)^{\rm{T}}} ，\end{split} $

(13)

状态向量的协方差矩阵表达式如下：

$ \begin{split} {P_w} = &\sum\limits_{i = 0}^{2n} {{\varphi _{ic}}} \left( {\chi _{i,k\left| {k - 1} \right.}^{} - {{\hat w}_{k\left| {k - 1} \right.}}} \right) - \\ & {{\hat y}_k}{\left( {\chi _{i,k\left| {k - 1} \right.}^{\rm{T}}X\left( k \right) - f\left( {\chi _{i,k\left| {k - 1} \right.}^{\rm{T}}X\left( {k - 1} \right)} \right)} \right)^{\rm{T}}} 。\end{split} $

(14)

5）更新参数状态向量及协方差矩阵

构建卡尔曼增益矩阵的表达式如下：

$ {K_k} = {P_w}{\left( {{P_y}} \right)^{ - 1}}，$

(15)

待识别船舶航行定位参数的状态向量更新表达式如下：

$ {\hat w_k} = {\hat w_{k\left| {k - 1} \right.}} + {K_k}\left( {{{\hat y}_k} - {{\hat y}_{k\left| {k - 1} \right.}}} \right)，$

(16)

船舶航行定位参数状态向量的协方差矩阵为：

$ {P_k} = {P_{k\left| {k - 1} \right.}} - {K_k}{P_y}K_k^{\rm{T}}。$

(17)

通过以上过程，对船舶航行定位参数进行实时更新，输出船舶航行定位参数识别结果。

1.3 基于粒子群算法的定位参数识别优化

为了使船舶航行定位参数识别的数学模型获取最佳的参数识别结果，利用粒子群优化算法对数学模型的参数进行优化，获取无迹卡尔曼滤波的初始状态误差的协方差矩阵P₀。x_i与v_i分别为粒子位置以及移动速度；q_i与g_i分别为粒子的当前最优位置以及全局最优位置。粒子移动速度和位置的更新公式如下：

$ {v_{i + 1}} = \omega {v_i} + {c_1}{r_1}\left( {{q_i} - {x_i}} \right) + {c_2}{r_2}\left( {{g_i} - {x_i}} \right)，$

(18)

$ {x_{i + 1}} = {x_i} + {v_{i + 1}}。$

(19)

式中： $ {c_1} $ 、 $ {c_2} $ 与 $ {r_1} $ 、 $ {r_2} $ 分别为学习因子和随机数； $ \omega $ 为惯性权重。惯性权重的更新公式如下：

$ \omega = {\omega _{\max }} - k\left( {{\omega _{\max }} - {\omega _{\min }}} \right)/{k_{\max }} 。$

(20)

式中： $ k $ 与 $ {k_{\max }} $ 分别为迭代次数和最大迭代次数； $ {\omega _{\max }} $ 与 $ {\omega _{\min }} $ 分别为最大权重和最小权重。

粒子群优化算法的优化目标为无迹卡尔曼滤波算法的初始状态误差的协方差矩阵。随机生成粒子群，利用粒子的适应度函数，选择粒子的最优位置。选取船舶航行定位预测值和测量值的绝对误差，作为粒子的适应度值，确定卡尔曼滤波算法的协方差矩阵。利用所确定的协方差矩阵，更新待识别参数的状态向量，输出最终的船舶航行定位参数识别结果。

2 实例分析

为了验证设计模型的参数识别性能，选取某执行环保任务的工作船作为研究对象。该船的用途为回收浮油、回收固体垃圾、控制浮油污染。该船舶回收溢油作业的航速为1～5 kn，续航力为500 nmile。选取Matlab，作为船舶航行定位参数识别的测试软件。

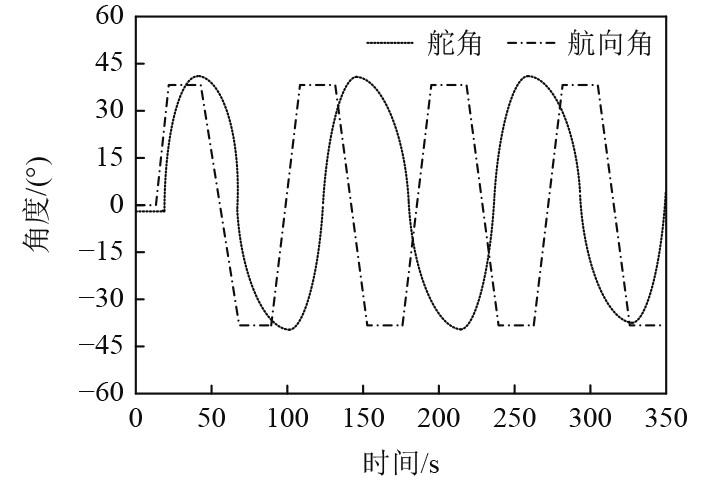
设置船舶的航行速度为12 m/s，对该船舶进行25°/25°的Z型操舵实验。船舶操舵实验的结果如图1所示。由图1可知，采用本文模型构建的船舶航行动力定位系统的非线性运动方程，可以模拟船舶的实际航行情况。船舶航行动力定位系统具有较高的可操纵性，满足船舶的基本运动规律，适用于后续的参数识别。

采用本文模型对船舶航行定位参数识别，参数识别结果如图2所示。可知，采用本文模型可以有效识别船舶航行的船舶惯性矩阵等定位参数。

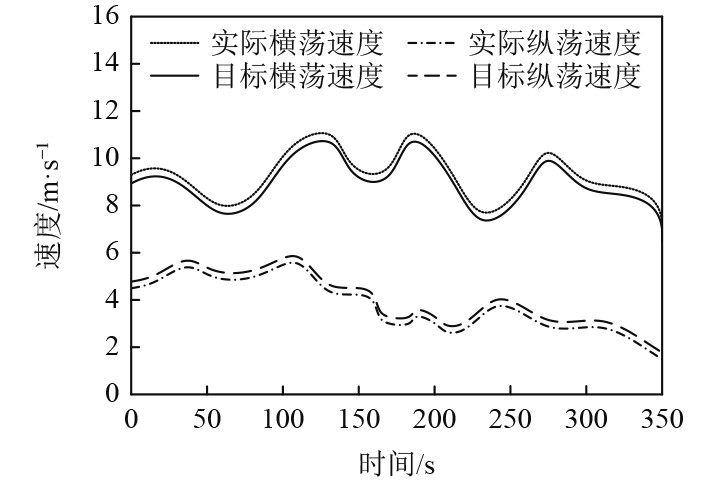
依据本文模型对船舶航行定位参数的识别结果，确定船舶航行时的横荡速度和纵荡速度，将实际速度结果与目标速度对比，对比结果如图3所示。可知，依据本文模型的船舶航行定位参数识别结果，船舶横荡速度和纵荡速度的实际结果与目标速度相差较小。实验结果表明，采用本文模型可以依据船舶航行定位参数识别结果，提升船舶的航行性能，缩小船舶航行实际速度与目标速度之间的差异。本文模型可以精准识别船舶航行定位参数，识别精度较高，满足船舶航行的实际需求。

采用本文模型依据船舶航行定位参数识别结果，进行船舶航行定位测试。船舶航行的航迹图如图4所示。结果表明，采用本文模型识别船舶航行定位参数，船舶航行定位结果与航行目标相差较小。

3 结　语

本文探讨船舶航行动力定位系统的非线性运动方程，设计了识别船舶航行动力定位系统参数的数学模型，利用粒子群优化算法，优化所构建的参数识别模型，提升船舶航行动力定位系统的参数识别性能。通过实验验证，该模型可以满足船舶航行动力定位系统的参数识别需求，提升船舶动力定位系统的运行性能，利用精准的航行定位结果，保障船舶依据目标航行轨迹精准航行。