2. 北京机械工业自动化研究所有限公司,北京 100120;
3. 大连船舶重工集团有限公司,辽宁 大连 116021
2. Beijing Machinery Industry Automation Research Intitute Co., Ltd., Beijing 100120, China;
3. Dalian Shipbuilding Industry Corporation Co., Ltd., Dalian 116021, China
惯性导航系统(INS)作为自主式导航系统,具有良好的隐蔽性、较高的短时导航精度、连续的信号输出等特点,且能提供平台自身的姿态数据,但长时间运行存在累积误差。卫星导航能够提供精确的定位信息,有效辅助惯导提高系统精度,但由于卫星导航抗干扰能力有限,在受到干扰下难以可靠精确地定位授时。在卫星导航拒止情况下,采用数据链/惯导的组合导航系统,能够在一定程度上提高系统整体导航定位精度和可靠性[1-2]。
数据链导航系统的基本原理是基于伪码测距进行定位,这与卫星导航系统原理相同。编队中,利用数据链导航可实现相对/绝对导航,数据链导航可一定程度上弥补惯导长时间无法进行校准和卫星导航特殊情况下受干扰的状况,但自身也受编队导航源几何位置分布、时间质量等影响[3]。
因此,针对数据链导航功能存在的不足,综合考虑导航定位的精度与可靠性,构建数据链/惯导/卫导多源融合导航系统,以提高系统导航的实时性并扩展导航区域范围。完成导航系统功能设计、滤波算法研究,最终通过仿真验证系统的定位精度、实时性、可靠性提高效果。
1 组合导航系统功能设计数据链导航作为一种导航手段,能够提供较高精度导航信息,但存在一些不足:1)垂向定位精度较低;2)无法提供平台姿态信息且位置信息更新率较低;3)如不在编队导航中引入地理基准,则无地理导航能力,给使用带来不便;4)系统工作区域受限。
1)数据链/惯导组合导航系统
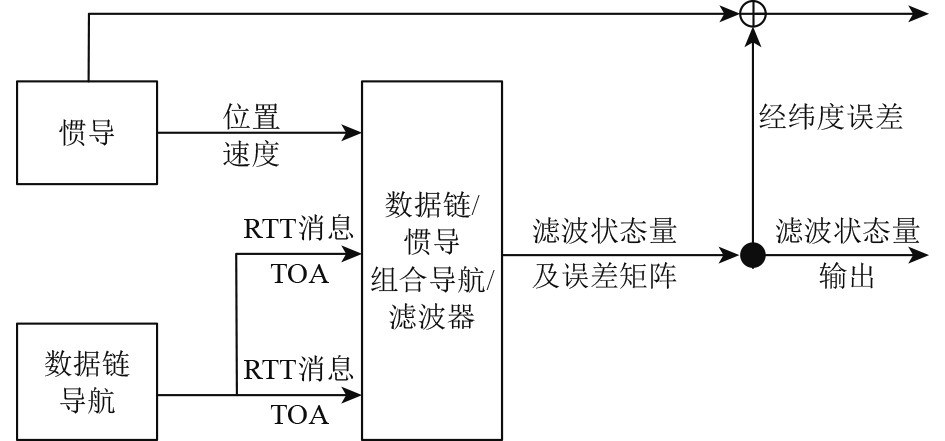
数据链/惯导组合导航是指通过编队中各个成员按一定周期向其他成员发送P消息,某一成员接收到其他成员消息后,根据测量得到TOA信息,结合自身惯导系统的信息,采用数据链/惯导组合导航滤波器,对成员自身的位置、速度、钟差等状态量进行实时滤波估计,从而得到成员之间相对位置信息[4-6]。结构如图1所示。
|
图 1 数据链/惯导组合导航系统滤波器结构 Fig. 1 Filter structure of data link / inertial navigation system |
选取的状态量为:平台误差角、速度、位置、陀螺漂移、加速度计误差以及信号接收机的时钟偏差和时钟偏差率。
卡尔曼滤波的状态方程为惯导系统的误差传播方程,滤波器的观测量确定为:数据链的TOA伪距与惯导计算的伪距之差、TOA伪距与源位置计算的伪距之差。则系统观测方程为:
| $ \begin{gathered} {Z_\rho } = {\rho _{TOA}} - {\rho _{SINS}} = \\ {a_\lambda }\delta \lambda + {a_L}\delta L + {a_h}\delta h + \delta t + {\nu _\rho }。\\ \end{gathered} $ |
其中:
2)数据链与卫导选取原则
数据链导航与卫导工作原理相似,通过故障检测与容错设计方式进行数据链导航与卫星导航选取。基于选取的结果再与惯导进行组合,对于平台整体导航能力的提升具有良好的应用价值。
3)数据链/惯导/卫导组合导航系统
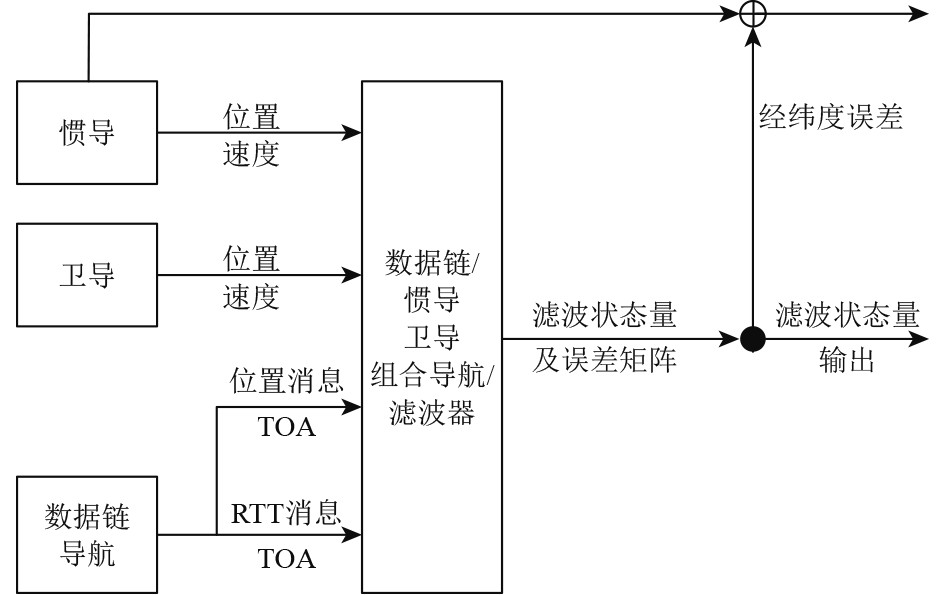
数据链/惯导/卫导组合导航,首先进行数据链导航与卫导选取,结合自身惯导系统的信息以及接收到的卫导/数据链导航数据,采用组合导航滤波器,对成员自身的位置、速度、钟差等状态量进行实时滤波估计,从而得到成员之间相对位置信息。图2为该组合导航系统结构框图。
|
图 2 数据链/惯导/卫导组合导航系统滤波器结构 Fig. 2 Filter structure of data link / INS / GNSS integrated navigation system |
数据链/惯导/卫导组合导航系统中,容错设计旨在提高系统可靠性[7]。
数据链/卫导/SINS组合导航系统在实际使用中,卫导会因临时关闭、障碍遮挡、天气、干扰等原因,失去可用性。类似这种可恢复性突变故障,可采用基于
1)状态
考虑带有故障的离散动态系统数学模型:
| $ \left\{ \begin{gathered} X(k) = \varPhi (k,k - 1)X(k - 1) + \varGamma (k - 1)W(k - 1) ,\\ Z(k) = H(k)X(k) + V(k) + {f_{k,\varphi }}\eta 。\\ \end{gathered} \right. $ |
式中:
2)故障检测
针对数据链/卫导/SINS构成的分散滤波器,为每个姿态子滤波器增加故障检测模块。
一旦判定某子系统发生故障,该子系统数据不再进入主滤波器参与信息融合,对剩余未发生故障的子系统数据进行局部状态估计融合,得到组合导航输出。在系统检测出子系统故障完成故障隔离期间,对该子系统进行修复。若故障修复完毕,经故障恢复准则判定该子系统数据可靠,系统重新将该子系统数据纳入滤波器进行融合。
2.2 存在野值时的容错设计故障的检测、隔离是根据滤波器的故障检测函数值进行的[8-9]。
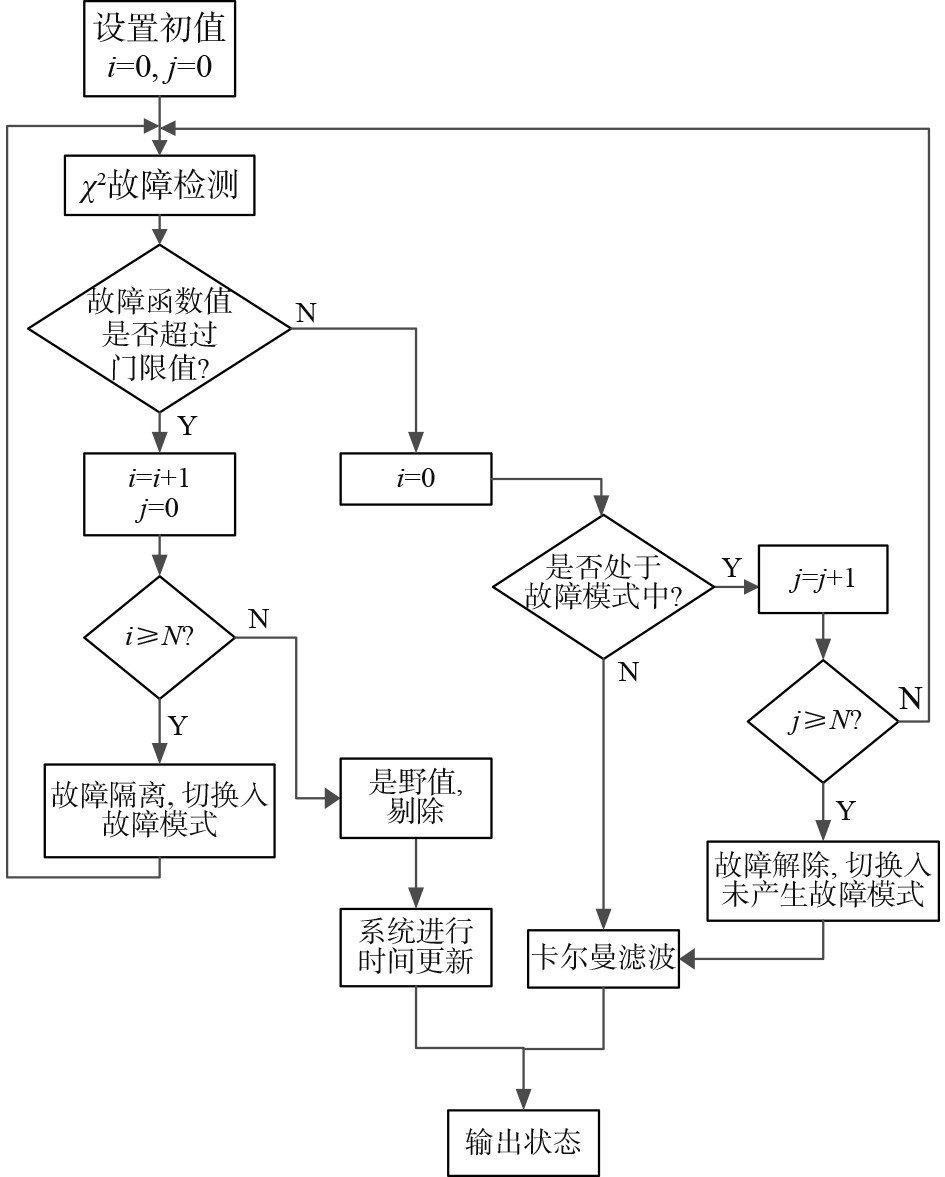
容错算法主要内容:故障发生判定规则——在连续的N个检测周期内(N的取值需要综合考虑故障检出率及导航系统性能),全部N个故障检测值大于等于阈值(预先设定),则判定系统发生故障。此时导航系统的工作模式切换到故障模式(仅针对某个故障的导航子系统),将该子系统输出的导航数据按照野值处理,直至故障恢复。故障恢复判定——连续的N个检测周期内,全部N个检测值小于阈值,则判定该子系统故障恢复。此时导航系统的工作模式切换到正常工作模式。图3为容错算法的流程图。
|
图 3 容错算法流程图 Fig. 3 Flow chart of fault-tolerant algorithm |
数据链/卫导/SINS组合导航的导航系统在使用时会使得某一子系统不定时暂时性失效或精度下降的情况,针对这种可能发生的使用场景,组合导航算法必须实现各子系统的在线故障隔离和重构的功能。组合导航分散滤波是一种可靠性高且各个子系统数据有相对独立性的算法,可以用于数据链/卫导/SINS组合导航系统。此外,该系统涉及多传感器,而不同类型传感器采样频率通常不同,即组合导航系统是多采样系统。
3.1 一种新的自适应分散Kalman滤波算法在滤波器中的导航系统标称模型与真实模型之间具有较大差异,这主要是由于导航系统本身是非线性时变系统,又不可避免的存在传感器误差。本文基于自适应在线调整渐消因子的方法,提出一种自适应多传感器组合导航系统分散滤波算法。
1)衰减记忆的集中滤波算法
时间、量测更新同步的具体方法如下:
| $ {{\boldsymbol{\hat X}}_c}{\text{(}}k|k - 1{\text{)}} = {{{{\boldsymbol{\varPhi }}}}_g}{\text{(}}k,k - 1{\text{)}}{{\boldsymbol{\hat X}}_c}{\text{(}}k - 1|k - 1{\text{)}} ,$ |
| $ \begin{gathered} {{\boldsymbol{P}}_c}{\text{(}}k|k - 1{\text{)}} = \lambda {\text{(}}k{\text{)}}{{\boldsymbol{\varPhi }}_g}{\text{(}}k,k - 1{\text{)}}{{\boldsymbol{P}}_c}{\text{(}}k - 1|k - 1{\text{)}} \cdot \\ {\text{ }}{\boldsymbol{\varPhi }}_g^{\text{T}}{\text{(}}k,k - 1{\text{)}} + {{\boldsymbol{\varGamma }}_g}{\text{(}}k - 1{\text{)}}{{\boldsymbol{Q}}_g}{\text{(}}k - 1{\text{)}}{\boldsymbol{\varGamma }}_g^{\text{T}}(k - 1{\text{)}},\\ \end{gathered} $ |
| $ {\boldsymbol{P}}_c^{ - 1}{\text{(}}k|k{\text{)}} = {\boldsymbol{P}}_c^{ - 1}{\text{(}}k|k - 1{\text{)}} + {\boldsymbol{H}}_c^{\rm{T}}{\text{(}}k{\text{)}}{\boldsymbol{R}}_c^{ - 1}{\text{(}}k{\text{)}}{{\boldsymbol{H}}_c}{\text{(}}k{\text{)}},$ |
| $ \begin{gathered} {{{\boldsymbol{\hat X}}}_c}{\text{(}}k|k{\text{)}} = {{\boldsymbol{P}}_c}{\text{(}}k|k{\text{)[}}{\boldsymbol{P}}_c^{ - 1}{\text{(}}k|k - 1{\text{)}}{{{\boldsymbol{\hat X}}}_c}{\text{(}}k|k - 1{\text{)}} + \\ {\text{ }}{\boldsymbol{H}}_c^{\rm{T}}{\text{(}}k{\text{)}}{\boldsymbol{R}}_c^{ - 1}{\text{(}}k{\text{)}}{{\boldsymbol{Z}}_c}{\text{(}}k{\text{)]}} 。\\ \end{gathered} $ |
2)渐消因子的自适应计算
渐消因子
| $ \lambda = \left\{ {\begin{array}{*{20}{c}} {{\lambda ^*}},&{{\lambda ^*} > 1} ,\\ 1,&{{\lambda ^*} \leqslant 1} 。\end{array}} \right. $ |
4)分散化自适应滤波算法
基于总体残差和局部残差分量分别调整渐消因子和信息分配因子的分散滤波自适应算法总结如下:
导航系统在初始化后,进行子滤波器
1)捷联惯导的数据链修正方法
①数据链/SINS组合模式
数据链导航方式与惯导系统在性能上具有很强的互补性,而且数据链提供的服务不受地域限制,能较为稳定地为惯导系统提供辅助导航信息。
数据链/惯性导航系统组合,按不同组合方法由多种方案。
第1种用数据链导航结果重调惯导。一般为用数据链导航给出的导航信息校准惯导系统的输出,或采用加权平均的方式将惯导和数据链输出的导航信息进行组合。
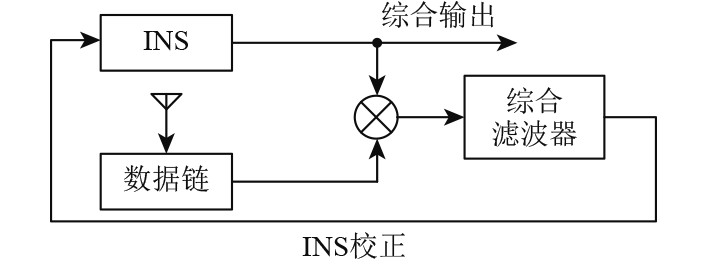
第2种数据链/惯导的位置、速度信息融合。基于卡尔曼滤波器进行位置、速度信息融合,组合导航系统框图如图4所示,系统量测值为数据链导航和惯导输出的位置、速度差,对惯导系统误差进行估计和校正。
|
图 4 数据链/INS位置、速度综合 Fig. 4 Position and velocity synthesis of data link / INS |
2)位置速度修正
采用卡尔曼滤波器进行数据链/SINS的组合,将惯性导航系统的误差方程作为系统状态方程。
位置速度综合的位置量测方程为:
| $ \begin{gathered} {{\boldsymbol{Z}}_{Gp}} = \left[ {\begin{array}{*{20}{l}} {({\phi _I} - {\phi _G}){R_M}} \\ {({\lambda _I} - {\lambda _G}){R_N}\cos {\phi _G}} \\ {{h_I} - {h_G}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{l}} {{R_M}\delta \phi + {\eta _n}} \\ {{R_N}\cos {\phi _G}\delta \lambda + {\eta _e}} \\ {\delta \,h + {\eta _u}} \end{array}} \right] = {{\boldsymbol{H}}_{Gp}}{\mathbf{X}} + {{\boldsymbol{V}}_{Gp}} 。\end{gathered} $ |
式中:
| $ {{\boldsymbol{H}}_{GP}} = \left[ {\begin{array}{*{20}{c}} {{\rm{diag}}\left[ {\begin{array}{*{20}{c}} {{R_M}}&{{R_N}\cos {\phi _G}}&1 \end{array}} \right]}&{{{\boldsymbol{O}}_{3 \times 12}}} \end{array}} \right],$ |
| $ {{\boldsymbol{V}}_{GP}} = {\left[ {\begin{array}{*{20}{c}} {{\eta _n}}&{{\eta _e}}&{{\eta _u}} \end{array}} \right]^{\text{T}}} 。$ |
定义速度量测矢量为:
| $ {{\boldsymbol{Z}}_{Gv}} = \left[ {\begin{array}{*{20}{c}} {{V_{Ie}} - {V_{Ge}}} \\ {{V_{In}} - {V_{Gn}}} \\ {{V_{Iu}} - {V_{Gu}}} \end{array}} \right] = {{\boldsymbol{H}}_{Gv}}{\boldsymbol{X}} + {{\boldsymbol{V}}_{Gv}} 。$ |
式中:
| $ {{\boldsymbol{H}}_{Gv}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{O}}_{3 \times 3}}}&{diag[\begin{array}{*{20}{c}} 1&1&1 \end{array}]}&{{{\boldsymbol{O}}_{3 \times 3}}} \end{array}} \right],$ |
| $ {{\boldsymbol{V}}_{Gv}} = {\left[ {\begin{array}{*{20}{c}} {\delta {v_e}}&{\delta {v_n}}&{\delta {v_u}} \end{array}} \right]^{\text{T}}} 。$ |
2)捷联惯导的卫星导航(卫导)修正方法
卫星导航(GPS、北斗)等导航方式,是目前应用较为广泛的导航策略,可方便为载体提供位置、速度信息测量,用以构成组合导航系统。
3)数据链/卫导/SINS组合导航
由于卫导导航与数据链导航的观测方程一致,因此卫导的加入并不会增加数据链/SINS组合导航系统可观性。然而卫导、数据链导航的导航原理不同,因此当某一种测量方式不可用时,可切换至另一种测量方式完成导航工作,构成组合导航系统敏感器机理冗余。
鉴于卫导对位置、速度测量精度较高、研究较为成熟,因此以卫导为主观测敏感器。当卫导出现故障时,切换至数据链进行导航,将是数据链/卫导/SINS组合导航的首选方式。
4 系统性能仿真验证1)仿真背景
在编队航行的环境下,共2艘船、2架飞机、1架无人机组成编队协同飞行(航行)。假设船配有高精度惯导系统与卫星导航系统、飞机与无人机配有中低精度惯导系统与卫星导航系统,编队导航成员处于数据链/卫导/惯导组合导航模式。在任务执行过程中,无人机卫导系统受到干扰,无法收到信号。因此无人机切换到数据链/惯导组合导航模式,其他编队成员仍处于数据链/卫导/惯导组合导航模式。
2)仿真条件
编队各组网成员的初始值设定如表1所示。设置船的航行轨迹为加速、匀速直航、转弯和匀速直航,设置飞机与无人机飞行轨迹为盘旋轨迹,仿真时长为1 h。假设所有成员的初始位置、速度、姿态误差均如表2所示。
|
|
表 1 各组网成员初始位置、速度、姿态设置 Tab.1 Initial oosition, speed, and posture settings for each retwork member |
|
|
表 2 初始误差设置 Tab.2 Initial error setting |
设置数据链导航相关误差:TOA测量12.5 ns,时钟短期精度50 ns中时间质量误差50 ns。惯性导航器件误差参数和卫导误差参数进行设置,如表3和表4所示。
|
|
表 3 各组网成员惯导/卫导误差参数 Tab.3 Inertial/satellite navigation error parameters of each network member |
|
|
表 4 各组网成员惯导/卫导误差参数 Tab.4 Inertial/satellite navigation error parameters of each network member |
3)仿真结果
由图5~图7可知,编队成员卫导信号受干扰的情况下,编队导航定位精度远高于单一平台的导航定位精度。
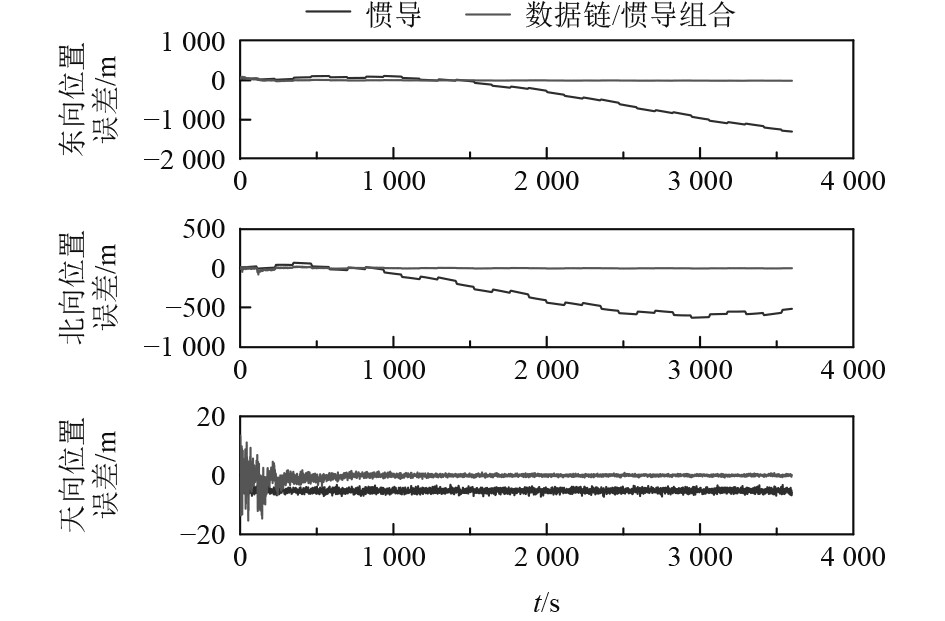
|
图 5 无人机受干扰后,无人机利用编队导航定位精度与平台导航对比 Fig. 5 The positioning accuracy comparison of UAV using formation navigation and self-navigation after interference |
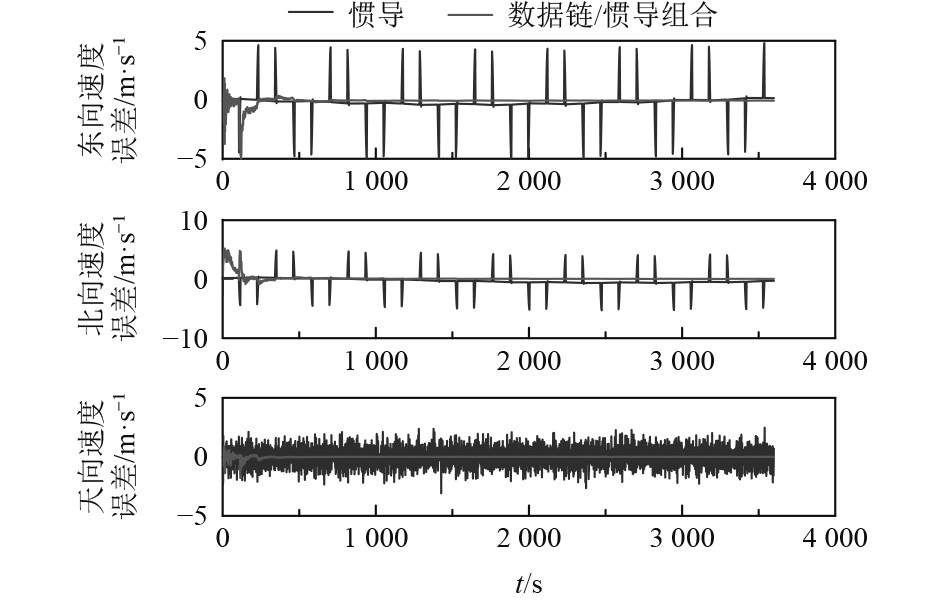
|
图 6 无人机受干扰后,无人机利用编队导航速度误差与平台导航对比 Fig. 6 The velocity accuracy comparison between UAV formation navigation and self-navigation after interference |
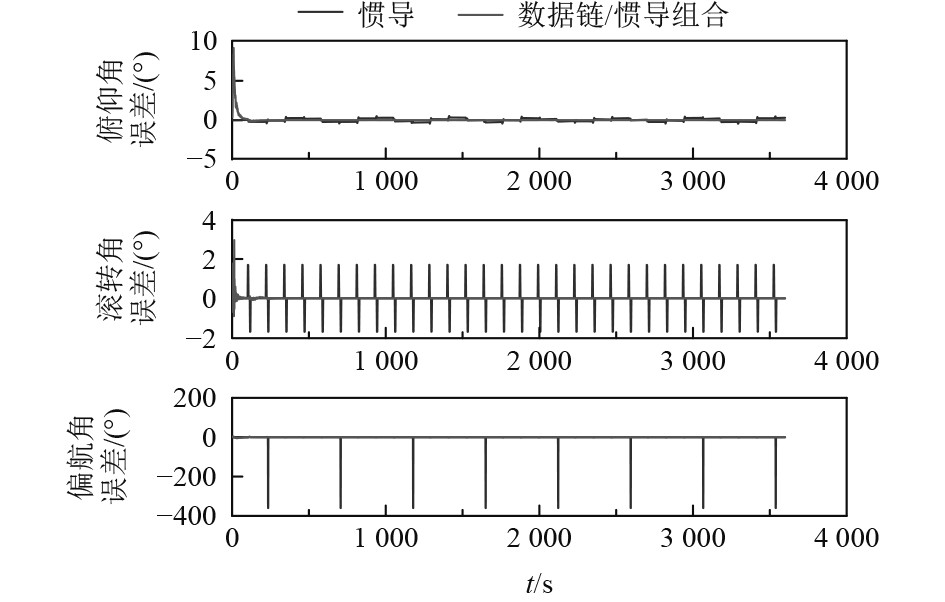
|
图 7 无人机受干扰后,无人机利用编队导航姿态误差与平台导航对比 Fig. 7 The attitude error comparison between UAV formation navigation and self-navigation after interference |
如图8~图11所示,在假定的仿真背景下,编队中船与飞机组合导航方式几乎未发生改变,因此导航精度几乎未发生改变。可得结论,编队成员卫导信号未受干扰的情况下,编队导航定位精度相当于单一平台的导航定位精度。
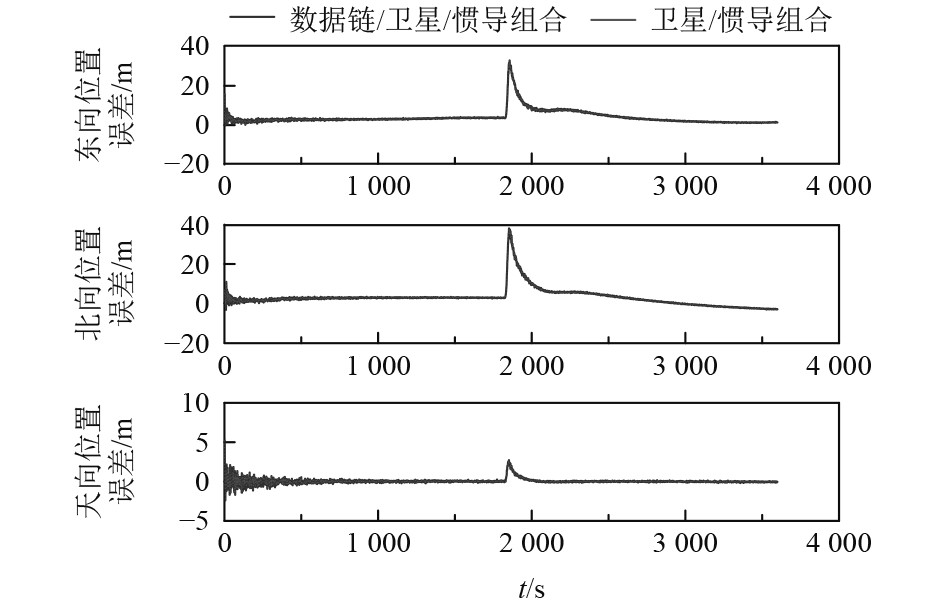
|
图 8 无人机受干扰后,船1利用编队导航定位精度与平台导航对比 Fig. 8 Comparison of positioning accuracy between formation navigation and platform navigation for ship 1 after UAV is disturbed |
|
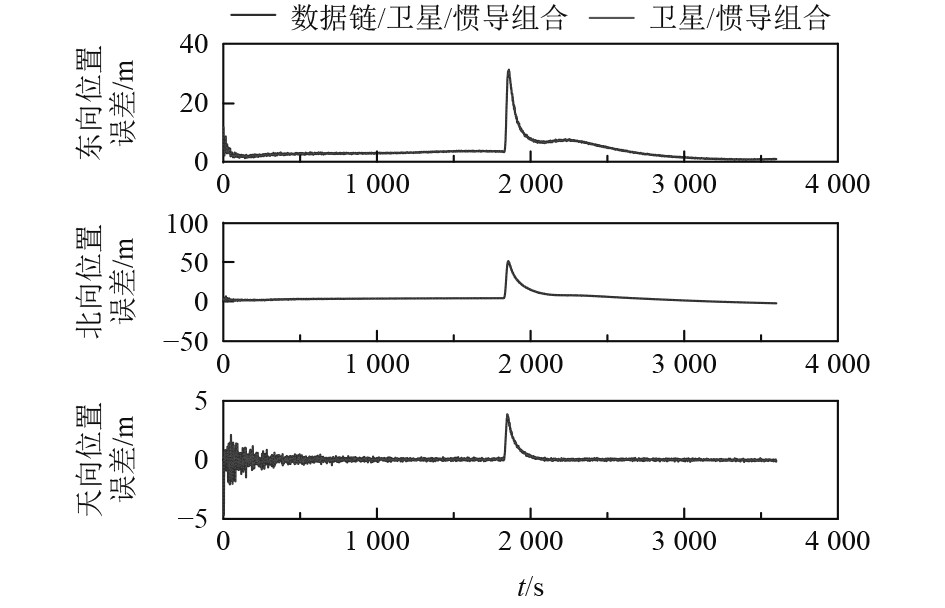
图 9 无人机受干扰后,船2利用编队导航定位精度与平台导航对比 Fig. 9 Comparison of positioning accuracy between formation navigation and platform navigation for ship 2 after UAV is disturbed |
|
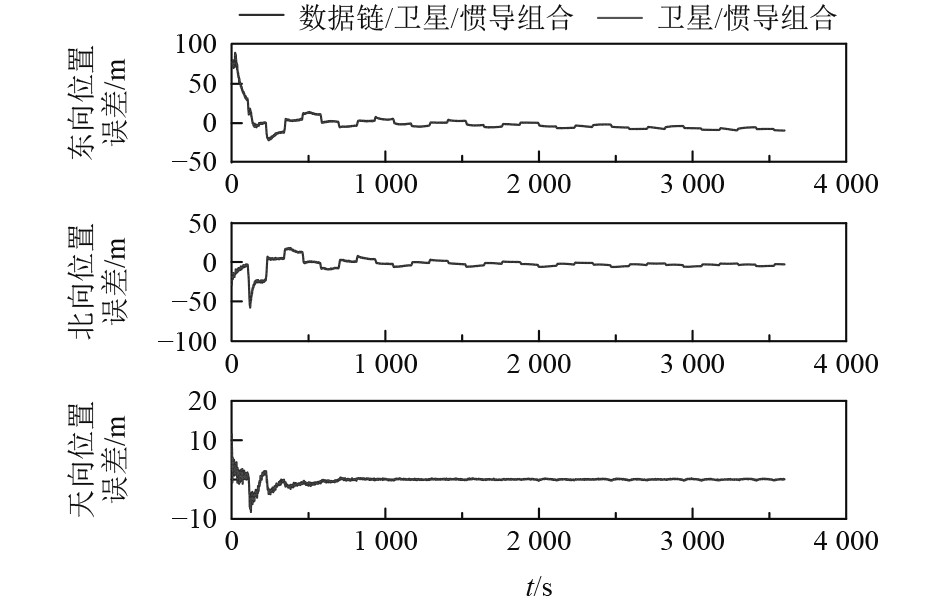
图 10 无人机受干扰后,飞机1利用编队导航定位精度与平台导航对比 Fig. 10 Comparison of positioning accuracy between formation navigation and platform navigation for plane 1 after UAV is disturbed |
|
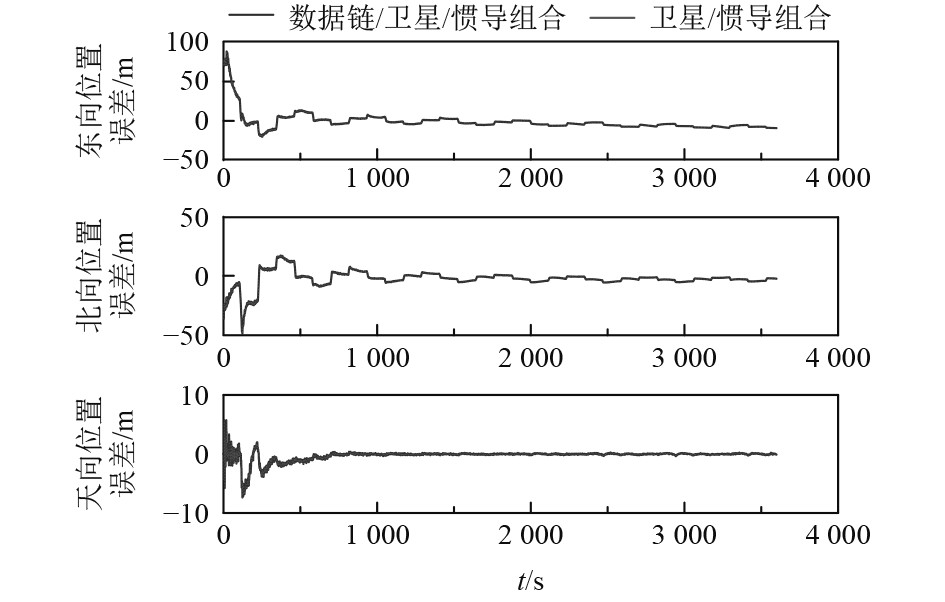
图 11 无人机受干扰后,飞机2利用编队导航定位精度与平台导航对比 Fig. 11 Comparison of positioning accuracy between formation navigation and platform navigation for plane 2 after UAV is disturbed |
综上,可得结论,编队导航定位精度不低于单一舰艇平台的导航定位精度。
5 结 语本文提出基于数据链的多源导航信息融合系统,主要采用联邦卡尔曼滤波结构,给出了一种自适应分散Kalman滤波算法,并基于残差
| [1] |
李玉成. 基于因子图的多源融合导航算法研究与实现[D]. 成都: 电子科技大学, 2022.
|
| [2] |
晏超然, 黄雪梅, 张康. 基于惯导/数据链测距的相对导航方法研究[J]. 计算机仿真, 2020, 37(5): 55-60+109. DOI:10.3969/j.issn.1006-9348.2020.05.012 |
| [3] |
周子寒. 基于数据链相对信息的无人车协同导航与路径规划算法研究[D]. 南京: 南京航空航天大学, 2021.
|
| [4] |
郝菁. 基于惯导/数据链协同的无人机集群导航定位算法研究[D]. 北京: 中国电子科技集团公司电子科学研究院, 2019.
|
| [5] |
王小刚, 郭继峰, 崔乃刚. 基于数据链的智能导弹协同定位方法 [J]. 中国惯性技术学报. 2009(3).
|
| [6] |
晁锐, 吴明强, 孟涛. 基于数据链的组合导航技术研究 [J]. 火力与指挥控制. 2009(3).
|
| [7] |
陈剑峰. 水下航行器组合导航系统容错方法研究[D]. 西安: 西北工业大学, 2007.
|
| [8] |
王其, 徐晓苏. 系统容错技术在水下航行器组合导航系统中的应用 [J]. 中国惯性技术学报. 2008(2).
|
| [9] |
熊智, 邵慧, 华冰, 等. 改进故障隔离的容错联邦滤波 [J]. 航空学报. 2015(3).
|
 2023, Vol. 45
2023, Vol. 45
