2. 海军装备部驻无锡地区军事代表室,江苏 无锡 214142
2. Naval Equipment Department Military Representative Office in Wuxi, Wuxi 214142, China
在援潜救生中,侧扫声呐可便携式搭载于参与救援的水面舰船,对事故区域进行扫测,为快速、高效、安全地实施援潜救生作业提供信息支撑,是水下搜索、考察等的重要工具。侧扫声呐拖体的水动力性能会影响产品的扫测效果,国内外学者针对相关问题进行了大量研究。袁毅之等[1]通过理论与模型试验相结合的方法,对带翼拖体的稳定性进行研究,得到各种带翼拖体正浮稳定拖曳点的位置。洪有财等[2]对声呐拖体的拖曳稳定性进行研究,推导出计算拖体静姿态角和静恢复力矩的公式,给出获得相关水动力参数的方法和途径。孙现有等[3]通过理论研究的方法讨论了浮式翼拖体的被动拖曳稳定性问题,为浮式翼拖体的结构设计提供了建议。卢军[4]采用理论与仿真相结合的方法对主动式声呐阵列的姿态进行预报。
本文采用有限元仿真的方法,对某便携式侧扫声呐拖体进行水动力仿真,分析声呐拖体的水动力性能,通过力矩平衡方程,预报声呐拖体的拖曳稳态纵倾角。对不同助潜翼和尾翼角度的声呐拖体模型进行仿真计算,最终将6 kn航速内声呐拖体的拖曳稳态纵倾角控制在10°以内,仿真结果与试验误差在10%以内,证明了仿真结果的准确性。仿真与试验相结合的方法可减少多次试验的时间与成本,为后期声呐拖体的拖曳姿态研究提供参考。
1 理论基础 1.1 守恒定律流体流动遵循基本的守恒定律,主要包括:质量守恒定律、动量守恒定律和能量守恒定律。处于湍流状态的流体,系统还要遵守附加的湍流运输方程[5]。
质量守恒方程:
| $ \frac{\partial \rho }{\partial t}+\nabla \left(\mathrm{\rho }{\boldsymbol{u}}\right)=0 。$ | (2) |
式中:ρ为流体密度;t为时间;u为速度矢量。
动量守恒定律:
| $ \rho \frac{\mathrm{d}\mathit{u}}{\mathrm{d}t}=\rho {\boldsymbol{f}}-\nabla {\boldsymbol{P}}+\nabla {\boldsymbol{\tau }} 。$ | (3) |
式中:f为作用在微元体上所有的所有质量上的力;τ为微元表面粘性应力;P为流体微元体上的压力。
能量守恒方程:
| $ \rho \frac{\mathrm{d}e}{\mathrm{d}t}=-{\boldsymbol{P}}\nabla {\boldsymbol{u}}+\mathrm{\varnothing }+q-\nabla q 。$ | (4) |
式中:
在进行水动力计算时,选择标准k-ε模型作为湍流计算模型,标准k-ε模型适用于高雷诺数的湍流计算,具备计算精度较高、使用范围广泛的特点[6]。
湍流动能k方程[7]为:
| $ \frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial {x}_{i}}\left(\rho {U}_{i}k\right)=\frac{\partial }{\partial {x}_{j}}\left(\frac{{u}_{eff}}{{\mathrm{\delta }}_{k}}\frac{\partial k}{\partial {x}_{k}}\right)+{G}_{k}-\mathrm{\rho }\varepsilon 。$ | (5) |
湍动能耗散率ε的方程为:
| $ \frac{\partial }{\partial t}\left(\rho \varepsilon \right)+\frac{\partial }{\partial {x}_{i}}\left(\rho {U}_{i}\varepsilon \right)=\frac{\partial }{\partial {x}_{j}}\left(\frac{{u}_{\mathrm{e}\mathrm{f}\mathrm{f}}}{{\mathrm{\delta }}_{\varepsilon }}\frac{\partial \varepsilon }{\partial {x}_{j}}\right)+{\rho} \Bigg(C_{{\varepsilon}1}{G}_{k}-{\mathrm{C}}_{\mathrm{\varepsilon }2}\frac{{\mathrm{\varepsilon }}^{2}}{k}\Bigg) 。$ | (6) |
式中:ρ为密度;t为时间;ueff为粘性系数;Gk为由层流速度梯度产生的湍流动能;Cε1、Cε2是常量;δk和δε是k方程和ε方程的湍流Prandtl数。
1.3 力矩平衡方程由于声呐拖体在水中拖曳时承受重力,浮力和水动力三者共同作用,在稳定状态下,三者相对于吊点的力矩应达到平衡,即和力矩为0。由文献[8]可知,拖体在水中的力矩平衡方程为:
| $ G{l}_{2}\mathrm{cos}{(\theta }_{n}+\theta )-F{l}_{1}\mathrm{cos}{(\theta }_{m}+\theta )+M=0 。$ | (7) |
式中:G为拖体重力;F为拖体浮力;
根据式(6),当确定了拖体重力、浮力、重心、浮心4种数据后,可绘制出稳态纵倾角
通过有限元仿真,可得到拖体与水平面呈不同攻角时,水动力相对于吊点产生的力矩,将此仿真曲线与式(6)的理论计算曲线绘制于同一张图中,曲线交点的横坐标即为拖体拖曳的稳态纵倾角。
2 便携式侧扫声呐拖体计算模型 2.1 便携式侧扫声呐拖体组成便携式侧扫声呐拖体主要包括:电子舱、换能器组件、手柄、拖揽头和附件(助潜翼、尾翼和垂尾)等,其示意图如图1所示。电子舱为水密壳体,为内部电子线路提供安装空间,电子线路部分与高低频换能器配合用于扫测水下目标物。助潜翼主要用于增加声呐拖体的下潜深度,尾翼用于增加横摇稳定性,垂尾主要用于增加转向稳定性。

|
图 1 便携式侧扫声呐拖体示意图 Fig. 1 Schematic diagram of portable side scan sonar towed body |
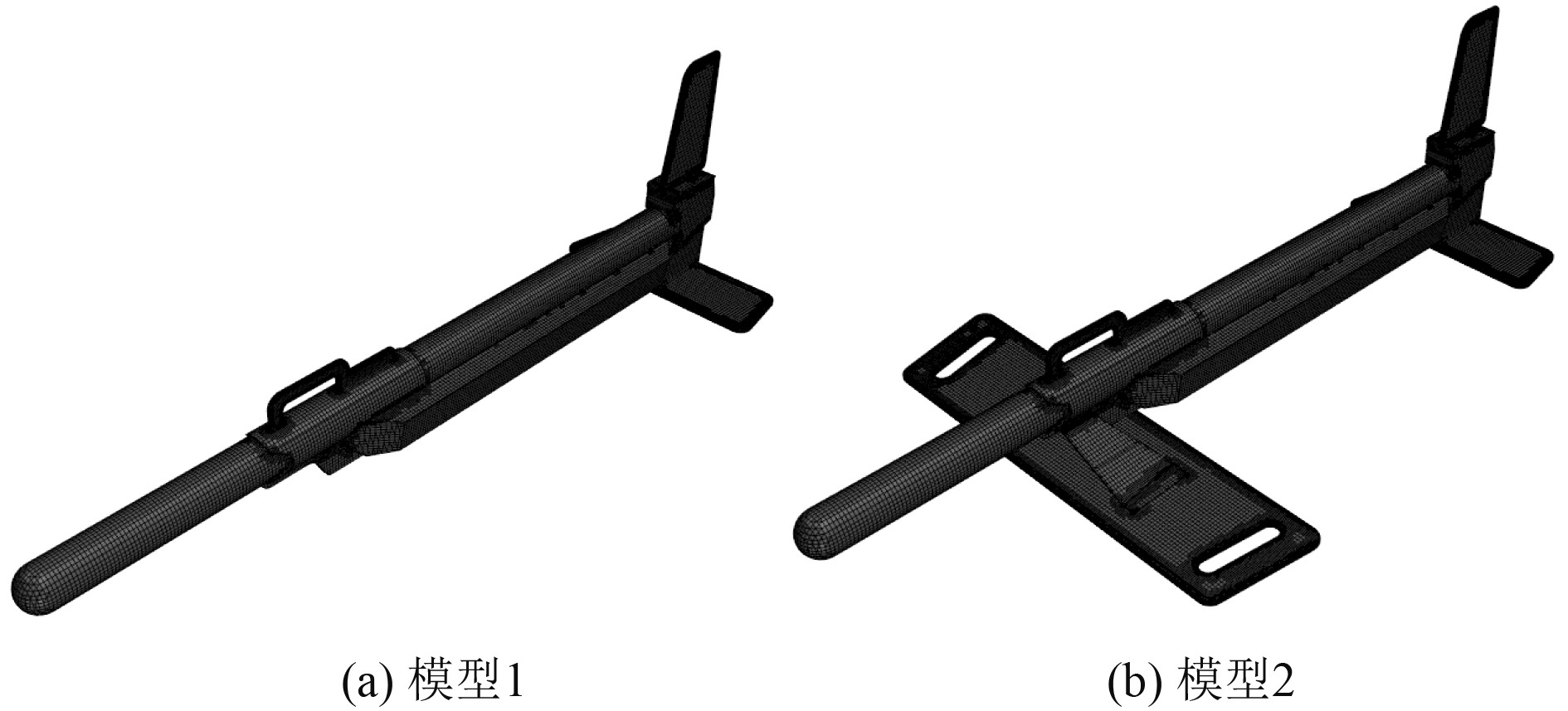
本文主要针对该便携式侧扫声呐拖体在不同攻角下的水动力力矩进行仿真。声呐拖体在水下工作时可选择不加装助潜翼(模型1)和加装助潜翼(模型2)2 种状态,分别适用于浅水与较深水拖曳,针对2 种模型分别进行仿真。
采用三维设计软件建立便携式侧扫声呐拖体的三维几何模型,对模型进行前处理,建立封闭的流体仿真模型,模型前处理完成后对其进行边界层设置和网格划分。便携式侧扫声呐拖体体网格模型如图2所示。
|
图 2 便携式侧扫声呐拖体有限元模型 Fig. 2 Finite element model of portable side scan sonar towed body |
由于助潜翼、尾翼与拖体之间的攻角不同,拖曳时形成的水动力不同,纵倾角也会不同。因此,在优化拖曳姿态时,对不同助潜翼和尾翼角度的模型也进行了计算,并与初步设计的模型2进行对比,以选取较优结果。计算模型如表1所示。
|
|
表 1 计算模型 Tab.1 Calculation model |
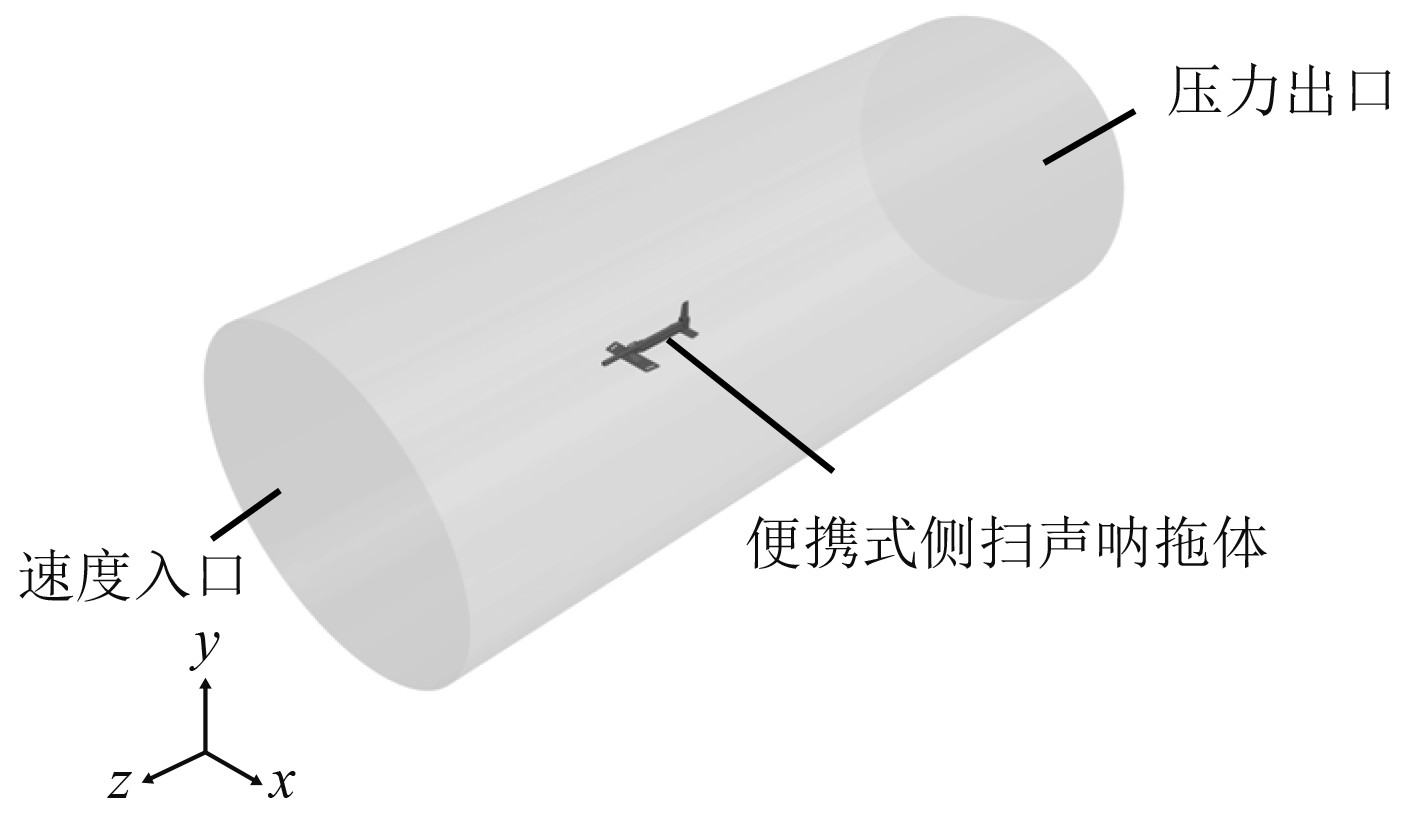
根据声呐拖体的主体形状选择水动力计算的外流域为圆柱形,设置流域入口为速度入口,出口为压力出口,流域外壁面设置为滑移壁面,其余默认为固壁。有限元计算边界条件及流域示意图如图3所示。
|
图 3 有限元计算边界条件及流域示意图 Fig. 3 Finite element calculation boundany conditions and watershed schematic diagram |
采用有限元软件对带附件的便携式侧扫声呐拖体模型进行水动力分析,6 kn航速下,侧扫声呐拖体表面速度分布与流线图如图4所示。6 kn航速下声呐拖体表面总压分布云图如图5所示。

|
图 4 声呐拖体表面速度分布与流线图 Fig. 4 Velocity distribution and streamline diagram of sonar surface |

|
图 5 声呐拖体表面总压分布云图 Fig. 5 Cloud chart of total pressure distribution on sonar surface |
由图4和图5可以看出,侧扫声呐拖体在助潜翼上表面周边、把手边缘、换能器前端、垂尾前部等位置流速较大。同时在这些位置出现了表面压力较大的负压区。通过改直角为圆角,增大圆角等方案,可使结构更圆滑,从而减小流阻力。
3.2 水动力性能计算为研究不同角度的助潜翼和尾翼对拖体水动力的影响,将仿真得到的水动力分为垂向(垂直水平面)和水平(迎流)2 个方向,得到6 kn速度内模型1~模型5水平与垂直方向的水动力变化曲线,如图6所示。

|
图 6 水动力仿真结果 Fig. 6 Hydrodynamic simulation results |
可知:模型1声呐拖体不加装助潜翼时,主要受水平方向的流阻力作用,垂向力近似为0,此时声呐拖体仅靠自重下沉,下沉深度较浅,可用于浅水拖曳;随着速度的增加,水平力与垂向力均增加,且垂向力增加较显著;对比模型3~模型5可以看出助潜翼角度增加,垂向力增加显著,说明助潜翼对增加声呐拖体的下沉深度有较大作用。但助潜翼和尾翼角度并不能无限制增大,因为当角度达到一定程度时,相应垂向力的增加效果会减弱。此时水平力会增加较为明显,因此应当综合考虑2 个方向的力,选取合适角度的助潜翼和尾翼。
4 拖曳姿态的仿真与试验数据对比由于模型1未加装助潜翼,水动力对声呐拖体的影响较小,在设计时控制重力和浮力的力矩平衡后,拖曳姿态较好,因此本文主要研究加装助潜翼的声呐拖体拖曳纵倾角。
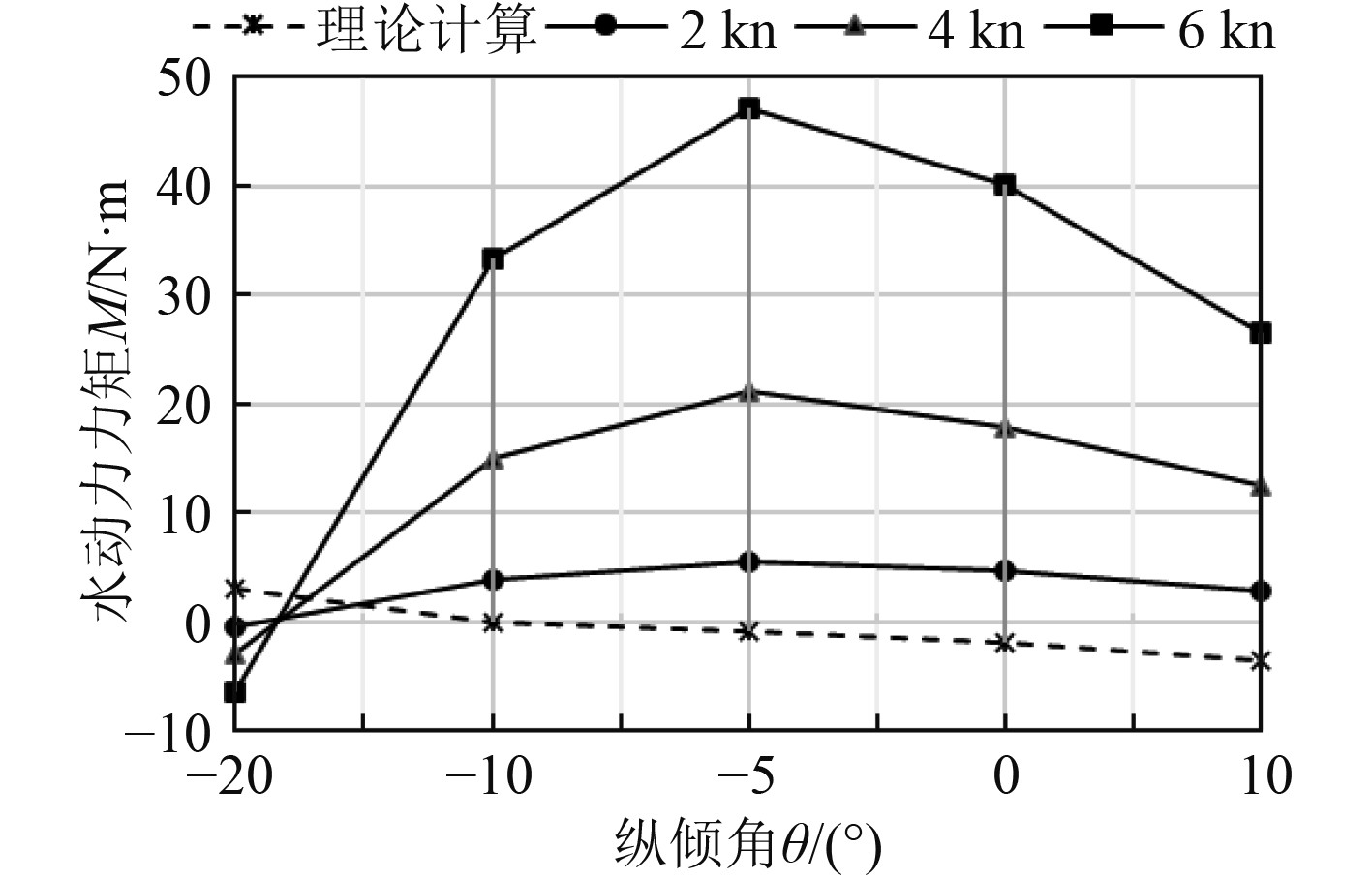
对带助潜翼的模型2进行拖曳纵倾角仿真与试验研究。首先,通过水动力仿真得到拖体与水平面呈不同攻角(拖体仰首时攻角取正值,俯首时攻角取负值)时的水动力力矩,得到1组攻角与水动力力矩的仿真关系曲线1;再根据式(7)绘制出理论计算的纵倾角与水动力力矩的关系曲线2,曲线1和曲线2交点的横坐标即为不同速度下拖体的稳态纵倾角,仿真结果如图7所示。
|
图 7 模型2纵倾角与水动力力矩的关系曲线 Fig. 7 Relation curve between the trim angle and hydrodynamic moment of model 2 |
将声呐拖体在水中进行拖曳试验,得到声呐拖体在实际拖曳时的稳态纵倾角。将试验值与仿真值进行对比,结果见表2。
|
|
表 2 模型2纵倾角仿真与试验结果对比 Tab.2 Comparison of model 2 trim angle simulation and test results |
可以看出,模型2纵倾角度仿真数据与试验值误差较小,在10%以内,因此仿真结果具有可靠性,可为后期声呐拖体姿态的优化提供参考。
5 声呐拖体拖曳姿态优化根据表2可知,在6 kn拖曳速度下,拖体纵倾角为15°。由于尾翼与助潜翼分别位于吊点前后,产生的水动力力矩方向相反,可通过不断优化助潜翼与尾翼的角度对声呐的拖曳姿态进行调整,以优化拖体的拖曳姿态,减小其拖曳时的纵倾角。
对模型 3~模型 5进行水动力分析,计算不同速度下,模型 3~模型 5的拖曳稳态纵倾角、水动力力矩仿真结果如图8所示,纵倾角数据见表3。

|
图 8 模型 3~模型5纵倾角与水动力力矩的仿真曲线 Fig. 8 Simulation curve of trim angle and hydrodynamic moment of model 3~model 5 |
|
|
表 3 模型3~模型5纵倾角仿真结果 Tab.3 Simulation results of trim angle of model 3~model 5 |
由图8可以看出,当助潜翼角度为7°,尾翼为10°时(即模型 4),拖体纵倾角最小。在6 kn航速内纵倾角均小于10°,且该状态下声呐拖曳纵倾角变化较小,稳定性良好。另外,由图8(a)可以看出,模型3两种曲线有两处交点,此时应取交点横坐标为负值的结果,即拖体在俯首状态的结果。因为拖体下水后由于水动力的作用在拖曳时会呈俯首状态,在俯首时先达到稳定平衡状态。
为进一步验证模型4仿真结果的准确性,对模型4的实物拖体进行水下拖曳试验,将试验结果与仿真结果进行对比,见表4。
|
|
表 4 模型4的纵倾角仿真与试验对比 Tab.4 Comparison between simulation and test of trim angle of model 4 |
可以看出,模型4仿真结果与试验结果误差较小,小于10%,因此仿真结果具备准确性,可提前预报拖体的稳态纵倾角。
6 结 语本文针对一种新型的便携式侧扫声呐拖体进行水动力仿真与试验研究,得到以下结论:
1)通过理论与仿真相结合的方法可提前预报声呐拖体水下拖曳的稳态纵倾角,仿真结果与试验误差在10%以内,具备准确性,可为后期声呐拖体的拖曳姿态研究提供参考。
2)通过对助潜翼和尾翼的角度进行优化,得到一种水下拖曳稳态纵倾角较小的声呐拖体。加装助潜翼后,在6 kn航速内,该声呐拖体的拖曳稳态纵倾角在10°以内,且不同航速下的纵倾角变换较小,具备较好的拖曳稳定性。
3)助潜翼和尾翼角度增加可为声呐拖体提供较大的下沉力,但同时声呐拖体的迎流阻力也相应增加,且速度越大,水平力与垂向力增加也越明显,应根据拖缆拉力选取合适角度的助潜翼和尾翼。
| [1] |
袁毅之, 徐一中, 蔡丽华. 带翼声纳拖体的稳定性问题及三点拖曳方式[J]. 海洋工程, 1984(2): 48-57. YUAN Yi-zhi, XU Yi-zhong, CAI Li-hua. Stability of towed body of winged sonar and three-point towing mode[J]. The Ocean Engineering, 1984(2): 48-57. DOI:10.16483/j.issn.1005-9865.1984.02.005 |
| [2] |
洪有财, 陈小星, 龚凯, 等. 声纳拖体拖曳稳定性研究[J]. 声学与电子工程, 2013(2): 24-27. HONG You-cai, CHEN Xiao-xing, GONG Kai, et al. Study on towed stability of sonar towed body[J]. Acoustics and Electronics Engineering, 2013(2): 24-27. |
| [3] |
孙现有, 刘显龙. 浮式翼拖曳体总体设计与稳定性分析[J]. 水雷战与舰船防护, 2018, 26(1): 50-53. SUN Xian-you, LIU Xian-long. Overall design and stability analysis of floating wing towed body[J]. Mine Warfare & Ship Self-defence, 2018, 26(1): 50-53. |
| [4] |
卢军. 主动式声纳列阵拖曳系统姿态数值计算[J]. 海洋工程, 2001, 19(3): 85-90. DOI:10.16483/j.issn.1005-9865.2001.03.019 |
| [5] |
孙丽, 刘贵杰, 王猛, 等. AUV导流罩外流场数值仿真与几何参数优化[J]. 计算机仿真, 2011, 28(5): 188-192. SUN Li, LIU Gui-jie, WANG Meng, et al. Numerical simulation of external flow field and geometry parameters optimization of AUV dome on bow[J]. Computer Simulation, 2011, 28(5): 188-192. DOI:10.3969/j.issn.1006-9348.2011.05.046 |
| [6] |
杜礼明, 张进. 基于降低航行阻力的声呐导流罩外形优化[J]. 舰船科学技术, 2013, 35(4): 75-79. DU Li-ming, ZHANG Jin. Numerical optimization of sonar dome profile based on reducing its sailing resistance[J]. Ship science and technology, 2013, 35(4): 75-79. |
| [7] |
HSIEH.K T,. RAJAMANI.R K Mathematical model of the hydrocyclone based on physics of fluid flow[J]. AICHE Journal, 1991, 37(5): 735-746. DOI:10.1002/aic.690370511 |
| [8] |
黄一清, 许冲, 张沛心, 等. 拖体拖曳稳态纵倾角计算仿真及试验研究[J]. 船舶工程, 2022, 44(1): 137-141. HUANG Yi-qing, XU Chong, ZHANG Pei-xin, et al. Calculation simulation and experiment of steady-state trim angle of towed body[J]. Ship Engineering, 2022, 44(1): 137-141. |
 2023, Vol. 45
2023, Vol. 45
