当前,随着减震、降噪技术的发展,执行任务的水下目标也越来越难以被被动声呐探测到。主动声呐正在慢慢成为人类感知水下信息的重要探测手段。针对水下高速移动的小目标,回波信号一般是具有高多普勒频移的微弱信号。在输入信号为已知的确定信号时,由于匹配滤波器具有最大的输出信噪比,因此通常是高斯噪声背景下、理想信道中的最优滤波器[1]。赵智珊[2-3]提出了匹配滤波器频域自适应线谱增强(FDAMF),从匹配滤波器的自身特性和海洋信道两方面改善了检测性能。蒋西海[4]针对使用窄带信号作为发射信号存在可利用的带宽有限,不能充分发挥自适应线谱增强性能的问题,提出将FDAMF与宽带信号相结合来检测远程目标。
然而由于回波信号具有很高的多普勒频移,匹配滤波器对频移信号一般不具有适应性,回波和样本失配将导致多普勒滤波器检测性能下降,并且在混响背景,由于混响是由发射信号引起的,其频谱与发射信号几乎相同,单纯使用匹配滤波器进行信号检测,其性能也会严重退化。
针对上述问题,本文首先使用匹配滤波器组对动目标进行检测。为了能获得更好的检测效果,进一步对匹配滤波后的线谱使用被动检测手段——AR谱估计[5-6],并给出了实验仿真。结果表明,该方法在低信噪比下仍具有很好的检测效果。赵智珊[3]已经给出证明,目标信号在频域经过匹配滤波后输出为包含单频成分的信号分量,因此针对该单频信号分量可以使用功率谱估计对其进行检测。这么考虑主要是基于2个优点:1)输入信号经过匹配滤波器后,输出信噪比会达到最大,再使用谱分析的检测效果会优于单纯使用谱分析的检测效果;2)AR谱估计相比于经典谱估计具有分辨率高、适应短时数据和时变谱分析等优点。因此,使用匹配滤波和AR谱估计联合的水下动目标检测具有更好的检测效果。
1 匹配滤波器组在对匹配滤波器的设计过程中,采用的是滤波器输出信噪比最大准则[7],其思路是在发射信号确定,平稳噪声的相关函数或功率谱密度已知,采用最大信噪比准则,建立匹配滤波器的传输函数。
设信号模型:
| $ x(t) = s(t) + n(t),$ | (1) |
其中:
| $ y(t) = {s_y}(t) + {n_y}(t) ,$ | (2) |
根据输出信噪比最大准则:
| $ {R_{SN}} = \frac{S}{N} = \frac{{{{\left| {{s_y}(t)} \right|}^2}}}{{E\left[ {{{\left| {{n_y}(t)} \right|}^2}} \right]}} 。$ | (3) |
其中:
| $ {s_y}(t) = \frac{1}{{2{\text{π}} }}\int_{ - \infty }^\infty {S(\omega )H(\omega ){{{e}}^{{{j}}\omega t}}} {\text{d}}\omega ,$ | (4) |
| $ E\left[ {{{\left| {{n_y}(t)} \right|}^2}} \right] = \frac{1}{{2{\text{π}} }}\int_{ - \infty }^\infty {N(\omega ){{\left| {H(\omega )} \right|}^2}} {\text{d}}\omega ,$ | (5) |
于是式(3)可化为
| $ {R_{SN}} = \frac{{{{\left| {\dfrac{1}{{2{\text{π}} }}\displaystyle\int_{ - \infty }^\infty {S(\omega )H(\omega ){{{e}}^{{{j}}\omega t}}} {\text{d}}\omega } \right|}^2}}}{{\dfrac{1}{{2{\text{π}} }}\displaystyle\int_{ - \infty }^\infty {N(\omega ){{\left| {H(\omega )} \right|}^2}} {\text{d}}\omega }}。$ | (6) |
该问题可用变分法或许瓦尔兹不等式解决:
| $ \begin{split} & {\left| {\frac{1}{{2{\text{π}} }}\int_{ - \infty }^\infty {S(\omega )H(\omega ){e^{j\omega t}}} {\text{d}}\omega } \right|^2} \leqslant \frac{1}{{2{\text{π}} }}\int_{ - \infty }^\infty {{{\left| {H(\omega )} \right|}^2}} {\text{d}}\omega \times \\ & \quad\frac{1}{{2{\text{π}} }}\int_{ - \infty }^\infty {{{\left| {S(\omega ){e^{j\omega {t_0}}}} \right|}^2}} {\text{d}}\omega,\end{split} $ | (7) |
当
传输函数
冲激响应
由此可见白噪声背景下匹配滤波器的传输函数为输入的已知确定信号频谱的共轭,并附加相移
对于发射信号为多普勒敏感型信号,并且探测目标为高速运动目标时,就需要对信号进行相应的多普勒补偿,因此匹配滤波器组更适合对高速目标的检测。
其设计思路如下:通过建立不同的多普勒频移目标回波库,将接收到的信号与目标回波库的具有不同频偏的参考信号进行匹配滤波,通过最大值法,即可得到最优结果,从而估计出回波频率。
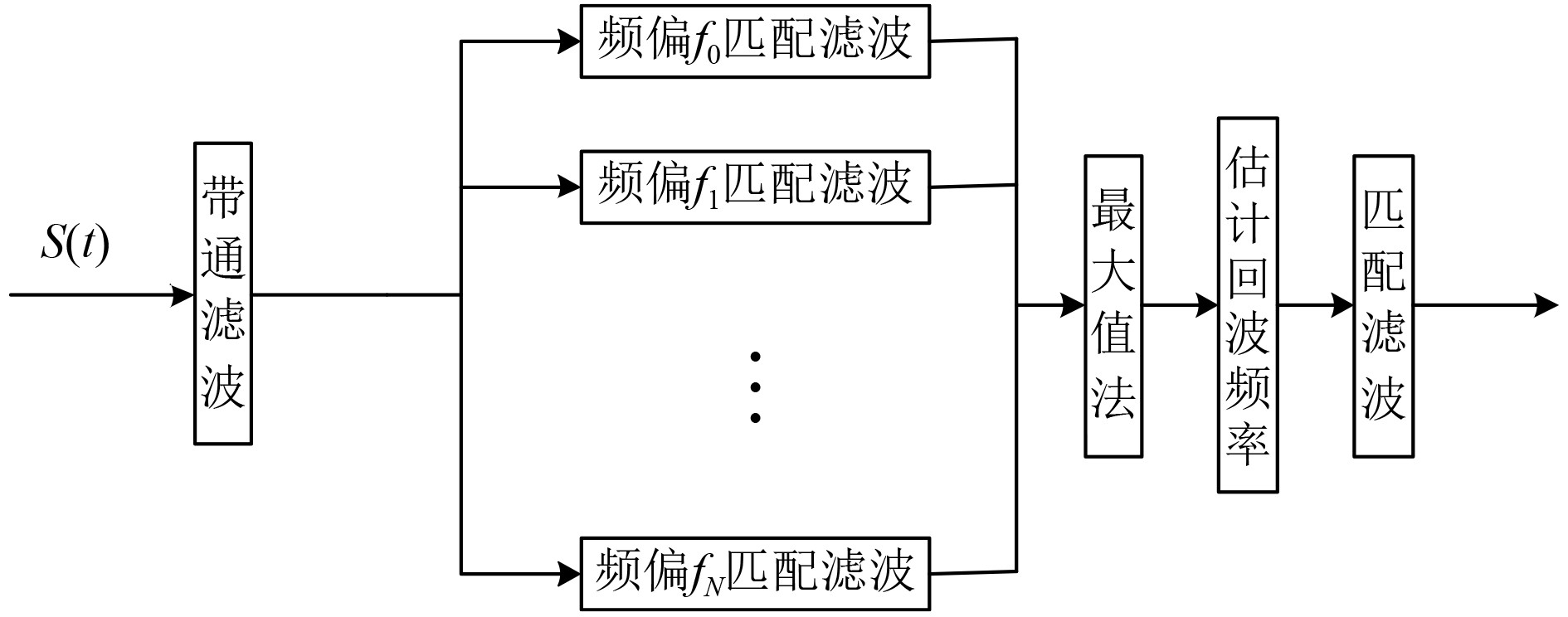
|
图 1 基于匹配滤波器组的目标检测流程 Fig. 1 Target detection process based on matched filter bank |
功率谱估计是根据有限的数据在频域内提取淹没在噪声中的有用信号。AR模型计算过程是线性的,使用熟知的高效算法实现,计算方便。除此之外,当估计出参数后,由参数构成的AR模型便自动产生、估计观察区间以外的数据。因此,AR谱估计在实用上仍受到广泛的重视。
时间序列
| $ {x_j} = {\alpha _1}{x_{j - 1}} + {\alpha _2}{x_{j - 2}} + \cdots + {\alpha _n}{x_{j - n}} + {\mu _j} 。$ | (8) |
其中:
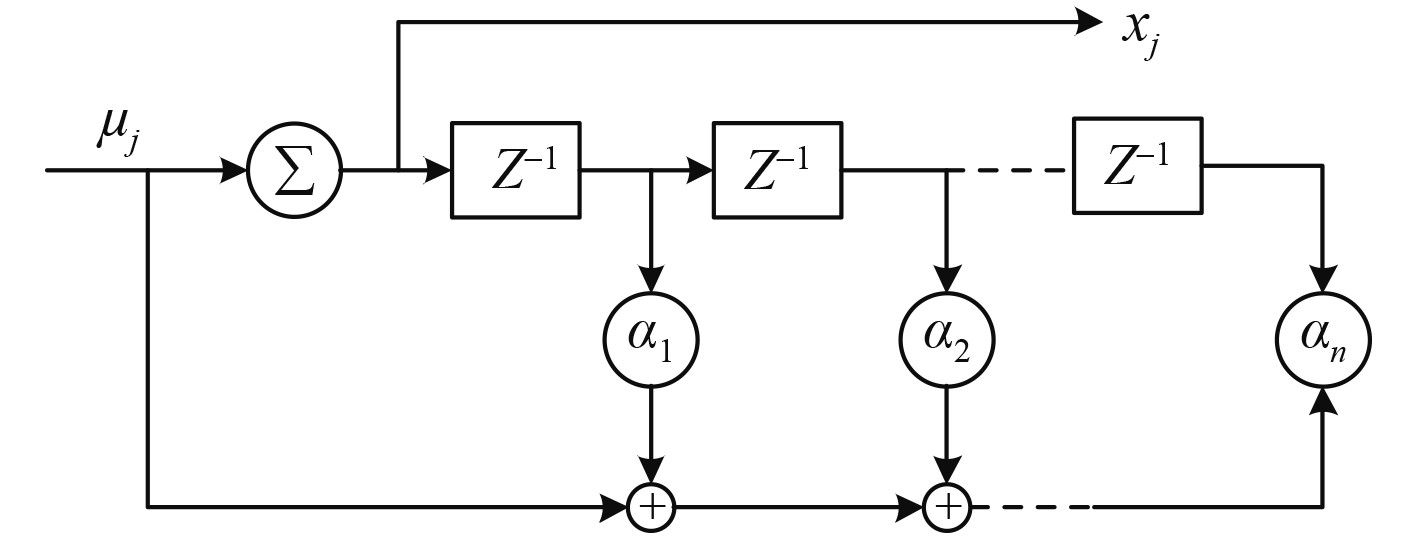
|
图 2 产生AR序列的模型 Fig. 2 Model for generating AR sequence |
也可写为:
| $ x(j) = - \sum\limits_{k = 1}^n {{\alpha _k}x(j - n) + {\mu _j}} ,$ | (9) |
| $ H(z) = \frac{1}{{A(z)}} = \frac{1}{{1 + \displaystyle\sum\limits_{k = 1}^n {{\alpha _k}{z^{ - 1}}} }},$ | (10) |
由此推出AR过程的功率谱密度为:
| $ {P_{AR}}(f) = {\left| {H({e^{j2{\text{π}} f\Delta t}})} \right|^2}{P_n}(f) = \frac{{{\sigma ^2}\Delta t}}{{{{\left| {1 + \displaystyle\sum\limits_{k = 1}^n {{a_k}{e^{j2{\text{π}} f\Delta t}}} } \right|}^2}}}。$ | (11) |
可以看出,只需估计出参数
设匹配滤波器组接收到频率
| $ x(t) = s(t) + n(t) ,$ | (12) |
| $ X({\omega _m}) = S({\omega _m}) + N(\omega )。$ | (13) |
其中:
在频域中,对回波在不同的频率段做匹配滤波:
| $ \left\{\begin{gathered} Y({\omega _1}) = H({\omega _1})X({\omega _m}) = H({\omega _1})S({\omega _m}) + H({\omega _1})N(\omega ) ,\\ Y({\omega _2}) = H({\omega _2})X({\omega _m}) = H({\omega _2})S({\omega _m}) + H({\omega _2})N(\omega ) ,\\ \qquad\qquad\qquad\qquad \vdots \\ Y({\omega _k}) = H({\omega _k})X({\omega _m}) = H({\omega _k})S({\omega _m}) + H({\omega _k})N(\omega ) 。\\ \end{gathered}\right. $ | (14) |
设在
| $ H({\omega _m}) = k{S^*}({\omega _m}){e^{ - j\omega {t_0}}} ,$ | (15) |
于是进一步有:
| $ \begin{split} Y({\omega _m}) =& kS({\omega _m}){S^*}({\omega _m}){e^{ - j\omega {t_0}}} + kN(\omega ){S^*}({\omega _m}){e^{ - j\omega {t_0}}} = \\& k{\left| {S({\omega _m})} \right|^2}{e^{ - j\omega {t_0}}} + kN(\omega ){S^*}({\omega _m}){e^{ - j\omega {t_0}}} 。\\[-10pt] \end{split} $ | (16) |
可以看出,目标信号在频域经过匹配滤波后输出
假设信号为:
| $ x(t) = A{e^{j{\omega _m}t}} + n(t) 。$ | (17) |
式中:A为信号的幅值;
| $ {\boldsymbol{X}}(n) = {[x(n),{\text{ }}x(n - 1),{\text{ }} \cdots {\text{ ,}}x(n - M + 1)]^{\rm{T}}} = Aa + v 。$ | (18) |
式中:
| $ \begin{split} {R_{XX}} = &E\left\{ {{\boldsymbol{X}}{{\boldsymbol{X}}^{\rm{H}}}} \right\} = E\left\{ {(A{\boldsymbol{a}} + {\boldsymbol{v}}){{(A{\boldsymbol{a}} + {\boldsymbol{v}})}^{\rm{H}}}} \right\}= \\ & {A^2}{\boldsymbol{a}}{{\boldsymbol{a}}^{\rm{H}}} + {\sigma ^2}I = {A^2}{{\boldsymbol{a}}^*}{{\boldsymbol{a}}^{\rm{T}}} + {\sigma ^2}{\boldsymbol{I}}, \end{split} $ | (19) |
为计算的方便,将上式写为:
| $ R = I + SNR \cdot {{\boldsymbol{a}}^*}{{\boldsymbol{a}}^{\rm{T}}},$ | (20) |
式中:
| $ {R^{ - 1}} = I - \frac{{SNR}}{{1 + SNR \cdot M}}{{\boldsymbol{a}}^*}{{\boldsymbol{a}}^{\rm{T}}} ,$ | (21) |
由
| $ {G_{AR}}(\omega ) = (1 - \frac{{SNR}}{{1 + SNR \cdot M}})/{\left| {1 - \frac{{SNR}}{{1 + SNR \cdot M}}{\mu _m}(\omega - {\omega _m})} \right|^2} ,$ | (22) |
式中,
式(22)表示谱密度,在
| $ {P_{AR}} = {G_{AR}}({\omega _0}) = (1 + SNR \cdot M)[1 + SNR \cdot (M - 1)]。$ | (23) |
可以看出,AR谱估计得到的线谱峰值是阶数和信噪比的函数,并且与信号信噪比的平方成正比,因此提高信噪比能够大幅度提高信号的谱峰峰值,使得对信号的检测更容易。
4 仿真数据分析仿真时假定目标以50 kn内的任意速度进行航行,使用频率为60 kHz的单频信号作为发射信号,目标回波信号的信噪比设定为−15 dB。
将回波信号和纯噪声分别通过匹配滤波器组后,取其最大值作为匹配得到的最终结果,由此可得图3 (a);将匹配滤波后的结果进一步使用AR谱估计可以得到图3 (b)。可以看出,在相同的信噪比下,联合检测对抑制噪声信号的效果更好。图4为在虚警概率为5%的条件下,2种方法的检测概率随着信噪比增加的变化趋势。可以看出,匹配滤波器与AR谱估计的联合检测效果要优于匹配滤波检测效果。
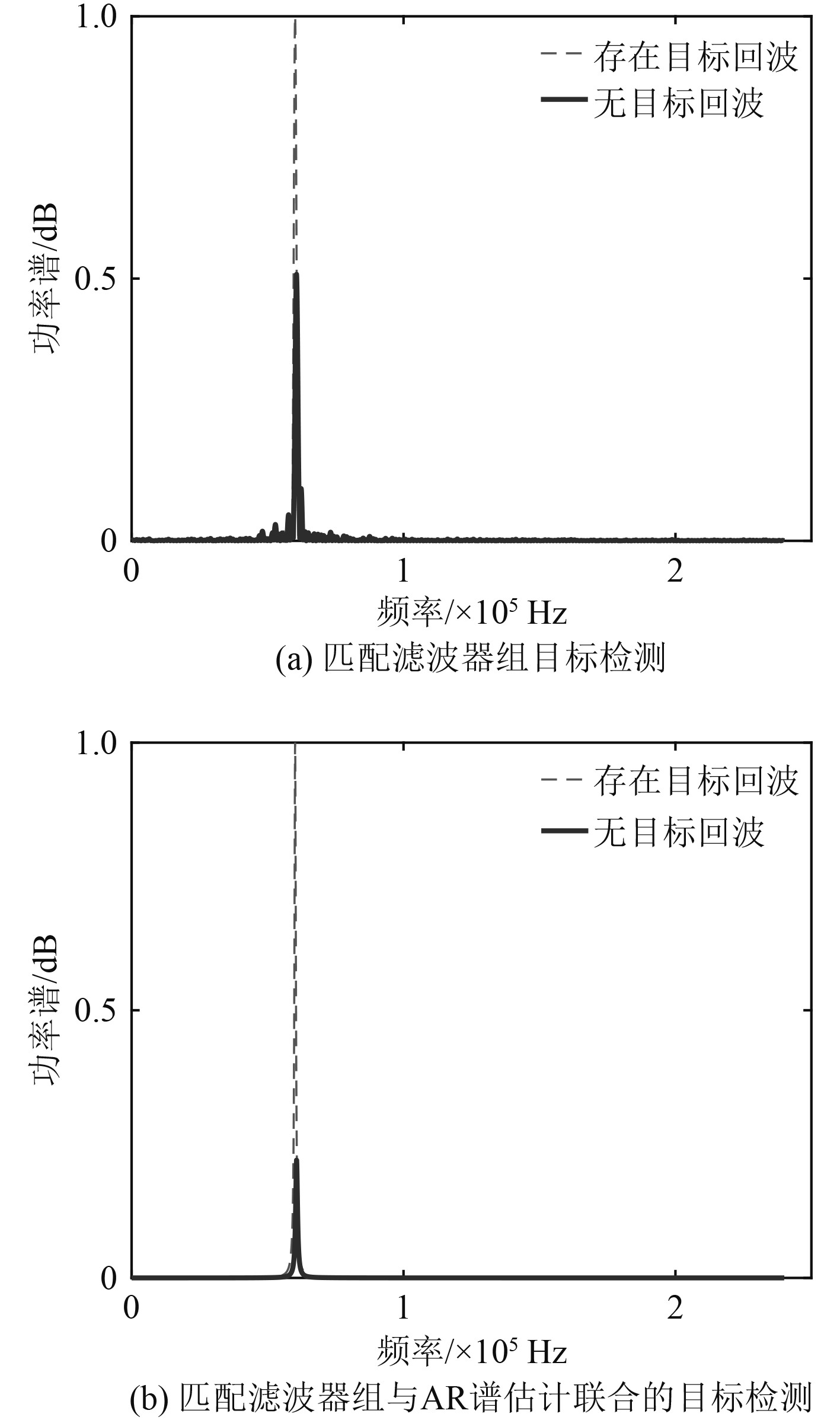
|
图 3 归一化后谱峰对比图 Fig. 3 Comparison of normalized spectral peaks |
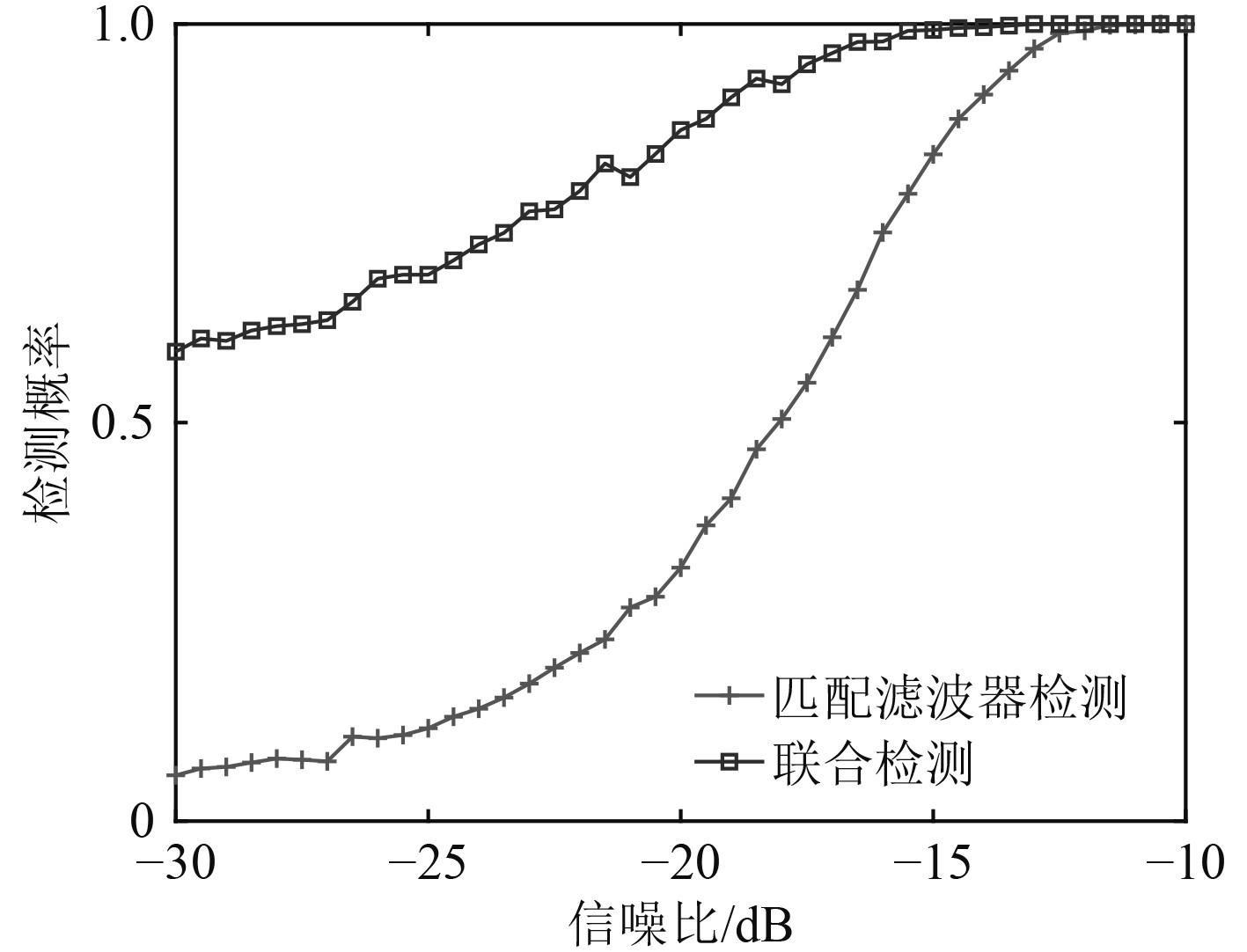
|
图 4 检测概率与输出信噪比的关系图 Fig. 4 Relationship between detection probability and output SNR |
本文介绍匹配滤波器组的基本思想和AR谱估计的基本知识,进一步分析指出匹配滤波后使用AR谱估计检测性能更优越的原理。通过仿真发现,联合检测方法能够提高回波信号的谱峰峰值,从而增加了检测概率,给出的ROC曲线验证了这一结论。
| [1] |
张蒙, 王海斌, 汪俊. 混响背景中回波信号检测方法研究[C]//. 中国声学学会水声学分会2019年学术会议论文集. 2019: 242−244.
|
| [2] |
ZHAO Z S, ZHAO A B, HUI J, et al. A frequency-domain adaptive matched filter for active sonar detection[J]. Sensors, 2017, 17(7): 1565. DOI:10.3390/s17071565 |
| [3] |
赵智珊. 基于匹配滤波器的频域自适应线谱增强技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [4] |
蒋西海, 王晓林, 严琪. 水下小孔径阵列远程目标检测方法研究[J]. 声学技术, 2021(1): 39-43. JIANG Xihai, WANG Xiaolin, YAN Qi. Research on remote target detection method of underwater small aperture array[J]. Technical Acoustics, 2021(1): 39-43. DOI:10.16300/j.cnki.1000-3630.2021.01.006 |
| [5] |
王志刚, 丁义明. 信噪比在AR模型定阶方法选择中的研究[J]. 数学物理学报, 2020, 40(3): 811-823. WANG Zhigang, DING Yiming. Research on signal-to-noise ratio in order selection of AR model[J]. Acta Mathematica Scientia, 2020, 40(3): 811-823. DOI:10.3969/j.issn.1003-3998.2020.03.024 |
| [6] |
KHORSHIDI S, KARIMI M, NEMATOLLAHI A R. New autoregressive (AR) order selection criteria based on the prediction error estimation[J]. Signal Processing, 2011, 91(10): 2359-2370. DOI:10.1016/j.sigpro.2011.04.021 |
| [7] |
赵树杰, 赵建勋. 信号检测与估计理论[M]. 北京: 清华大学出版社, 2005: 150−157.
|
| [8] |
刘晞远, 胡昊颖, 吴珊, 等. AR模型的谱分辨率及小信噪比下的性能分析[J]. 舰船电子工程, 2018(7): 126-131. LIU Xiyuan, HU Haoying, WU Shan. Performance Analysis on Spectrum Resolution Ratio and Small Noise-signal Ratio of AR Model-based Power Spectrum Estimation[J]. Ship Electronic Engineering, 2018(7): 126-131. DOI:10.3969/j.issn.1672-9730.2018.07.031 |
| [9] |
刘明晓, 王旭光. 基于Matlab实现的AR模型功率谱估计[J]. 电子设计工程, 2017(17): 129-132. LIU Ming-xiao, WANG Xu-guang. The realization of AR model power spectrum estimation based on MATLAB[J]. Electronic Design Engineering, 2017(17): 129-132. DOI:10.3969/j.issn.1674-6236.2017.17.031 |
 2023, Vol. 45
2023, Vol. 45
