风能属于发展前景较优的可再生能源,且其发展速度较快,在发电领域应用广泛[1]。船舶动力系统中,利用风能发电不仅可以缓解能源紧张问题,还能缓解水环境污染问题[2]。但风能发电的随机性与波动性较大,影响船舶动力系统发电的稳定性,导致船舶航向安全受到威胁[3]。为此,构建风力发电模型,分析船舶动力系统风力发电的影响因素。宋子秋等[4]通过分析风、冰与风力机的耦合特性,构造静态和动态的风力发电模型。该模型可有效分析冰载荷影响下,风力发电的变化情况,冰载荷越大,风力机输出功率越小,以变桨方式,可有效控制风力机冰载荷。季一润等[5]利用动态聚合建模方法,依据风机的发电特性,构造风力发电模型。该模型可有效分析风力发电情况。但上述模型在风速分布不均匀情况下,便无法精准描绘风机的动态特性,降低其适用范围。为解决上述问题,构建船舶动力系统自动化风力发电模型,通过结合风速型、风力机与发电机3个模型,充分考虑风速对船舶动力系统自动化风力发电的影响,提升风力模型构建效果。
1 船舶动力系统自动化风力发电模型 1.1 船舶动力系统的风速模型通过四分量法建立船舶动力系统的风速模型,公式如下:
| $ v = {v_m} + {v_g} + {v_r} + {v_a} 。$ | (1) |
其中:
| $ {v_m} = \bar v ,$ | (2) |
其中,
| $ {v_g} = \left\{ \begin{aligned} & 0,\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits{\mathop {}\nolimits_{}}t < {T_{gs}} ,\\ & \frac{{{v_{g,\max }}}}{2} - \frac{{{v_{g,\max }}}}{2}\cos \left( {\frac{{2{\text{π}} t - 2{\text{π}} {T_{gs}}}}{{{T_{ge}} - { T_{gs}}}}} \right),\mathop {}\nolimits{T_{gs}} \leqslant t < {T_{ge}} ,\\ & 0,\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits{\mathop {}\nolimits_{}}t \geqslant {T_{ge}}。\end{aligned} \right. $ | (3) |
其中:
| $ {v_r} = \left\{ \begin{aligned} & 0,\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits{\mathop {}\nolimits_{}}t < {T_{rs}} ,\\ & \frac{{{v_{r,\max }}}}{2} - \frac{{{v_{r,\max }}}}{2}\cos \left( {\frac{{2{\text{π}} t - 2{\text{π}} {T_{rs}}}}{{{T_{re}} - {T_{rs}}}}} \right),\mathop {}\nolimits{T_{rs}} \leqslant t < {T_{re}} ,\\ & 0,\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits\mathop {}\nolimits{\mathop {}\nolimits_{}}t \geqslant {T_{re}} 。\end{aligned} \right. $ | (4) |
其中:
船舶动力系统风力发电机主要由风轮、传动系统与感应电机组成。风轮负责收集风能[6],将其变更成机械能,经由传动系统带动感应电机转子旋转,生成电能[6]。按照贝兹理论,结合构建的风速模型,得到风轮模型,公式如下:
| $ P = \frac{{{\text{π}} \gamma \rho {v^3}{R^2}Y\left( {f,\kappa } \right)}}{2}。$ | (5) |
其中:
| $ f = \frac{{\omega R}}{v},$ | (6) |
其中,
风轮生成的风力矩为:
| $ N = \frac{P}{\omega } = \frac{{{\text{π}} \gamma \rho {v^2}{R^3}Y'\left( {f,\kappa } \right)}}{2} ,$ | (7) |
其中,
| $ Y'\left( {f,\kappa } \right) = \frac{{Y\left( {f,\kappa } \right)}}{f} 。$ | (8) |
船舶动力系统的传动系统负责连接风轮与感应电机,用于传输机械能[8]。依据构建的风轮模型,设计传动系统的运动方程为:
| $ {O}_{h}\frac{{\rm{d}}{\omega }_{h}}{{\rm{d}}t}=\frac{\eta }{\alpha }N-{N}_{G}\text{,}{O}_{l}\frac{{\rm{d}}{\omega }_{l}}{{\rm{d}}t}=N-\frac{\alpha }{\eta }{N}_{G} 。$ | (9) |
其中:
| $ {\omega _h} = \alpha {\omega _l} ,$ | (10) |
| $ \begin{split} &{O_h} = \frac{{\eta {O_1} + \eta {O_a}}}{{{\alpha ^2}}} + {O_2} + {O_b} ,\\ &{O_l} = {O_1} + {O_a} + \frac{{{\alpha ^2}{O_2} + {\alpha ^2}{O_b}}}{\eta } 。\end{split} $ | (11) |
其中:
依据构建的传动系统模型,构建船舶动力系统自动化风力发电的稳态模型,构建结果如下:
静态时,船舶动力系统自动化风力发电时的定子有功功率为:
| $ \begin{split}\hat P =& \left\{ \frac{{U_1^2}}{Z}O\left[ {\frac{{{c_1}c_2^2}}{{{s^2}}} + \frac{{x_m^2c_2^2}}{s} + {c_1}{{\left( {{x_2} + {x_m}} \right)}^2}} \right] \right.+\\ &\left.\frac{{{U_1}{U_2}}}{{sZ}}{x_m}\left( {A\sin \theta - B\cos \theta } \right) \right\} 。\end{split}$ | (12) |
其中:
| $ \left\{ \begin{split} &A = \frac{{{c_1}{c_2}}}{s} - \left( {{x_1}{x_m} + {x_m}{x_2}} \right),\\ &B = {x_m}\left( {{c_1} + \frac{{{c_2}}}{s}} \right) + {c_1}{x_2} + \frac{{{c_2}}}{s}{x_1} ,\\ &C = {\left( {A + B} \right)^2} 。\end{split} \right. $ | (13) |
船舶动力系统自动化风力发电时的定子无功功率为:
| $\begin{split} \hat Q =& \left\{ \frac{{U_1^2}}{Z}O\left[ {\left( {{x_2} + {x_m}} \right)\left( {{x_1}{x_m} + {x_m}{x_2}} \right) + \frac{{c_2^2}}{{{s^2}}}{{\left( {{x_1} + {x_m}} \right)}^2}} \right] +\right.\\ &\left.\frac{{{U_1}{U_2}}}{{sZ}}{x_m}\left( {A\sin \theta - B\cos \theta } \right) \right\},\\[-15pt]\end{split} $ | (14) |
结合式(12)与式(14)即船舶动力系统自动化风力发电的稳态模型。
依据传动系统模型,构建船舶动力系统自动化风力发电的暂态模型,构建结果如下:
暂态时,船舶动力系统自动化风力发电时的定子有功、无功功率
| $ {\widehat{Q}}_{s}=O\left({u}_{ds}{i}_{ds}+{u}_{qs}{i}_{qs}\right)\text{,}{\widehat{P}}_{s}=O\left({u}_{qs}{i}_{ds}-{u}_{ds}{i}_{qs}\right) 。$ | (15) |
其中:
暂态时,船舶动力系统自动化风力发电时的转子有功、无功功率
| $ {\widehat{Q}}_{r}=O\left({u}_{dr}{i}_{dr}+{u}_{qr}{i}_{qr}\right)\text{,}{\widehat{P}}_{r}=O\left({u}_{qr}{i}_{dr}-{u}_{dr}{i}_{qr}\right) 。$ | (16) |
其中,
令感应电机
| $ \left\{ \begin{split} & \frac{{{\rm{d}}{i_d}}}{{{\rm{d}}t}} = - \frac{{{R_s}}}{L}{i_d} + Ow{i_q} + \frac{1}{L}{u_d} ,\\ & \frac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}} = - \frac{{{R_s}}}{L}{i_d} - Ow\left( {{i_d} + \frac{1}{L}\phi } \right) + \frac{1}{L}{u_q} 。\end{split} \right. $ | (17) |
其中:
以Matlab作为仿真软件,在软件内根据船舶动力系统的特征和参数,建立动力系统的数学模型,并在其中添加风力发电模块。仿真过程中,设置船舶动力传输系统的传动速率为93%,动力系统效率为40%。构建的风力发电机组的基础参数包括:风轮直径为20 m,发电机额定功率为800 kW,发电机效率为35 %,电池组容量为500 kW·h,电池组电压等级为96 V低压直流。同时,该风力发电模块以某日的实际风速作为因素参数,将其与船舶动力系统进行耦合。具体的模型仿真风速变化情况如图1所示。
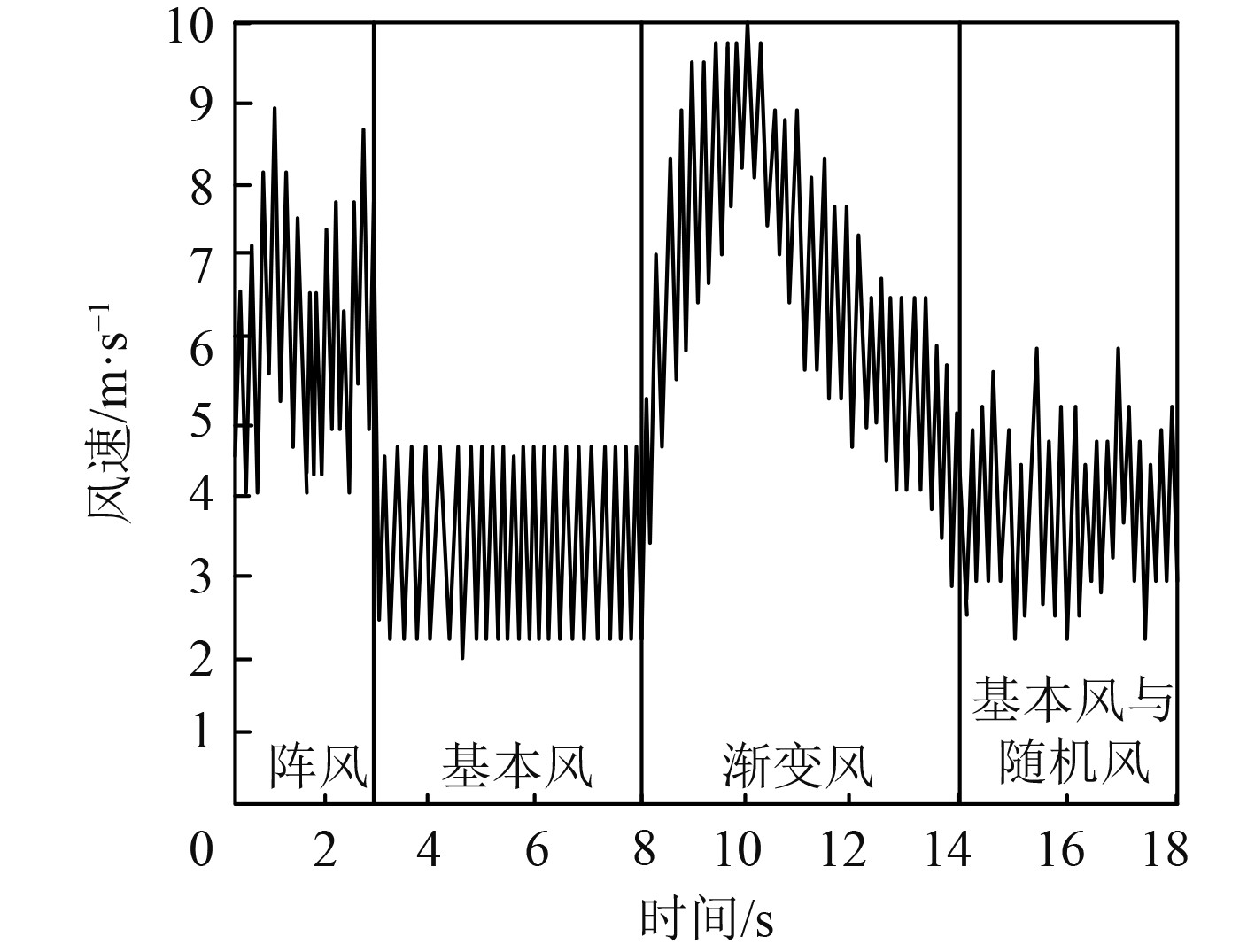
|
图 1 风速曲线 Fig. 1 Resultant wind speed curve |
由图1可知,本文模型可有效建立风速模型,由该风速曲线了解到:0~6 h风速较大且波动较大,范围在4~9 m/s左右。这个时间段内的风速较高,可能会对船舶和风力发电机组产生较大的风载荷和振动。6~11 h风速较小且波动较小,范围在2~5 m/s左右。这个时间段内的风速相对稳定,对船舶和风力发电机组产生的负荷和振动较小。11~15 h风速逐渐增大且波动范围较大,范围在2~10 m/s左右。这个时间段内的风速呈现逐渐增大的趋势,可能对船舶和风力发电机组产生不断增大的负载和振动。15~24 h风速波动区间在3~10 m/s左右。这个时间段内的风速呈现波动的特征,对船舶和风力发电机组的负载和振动产生影响。实验证明,本文模型可有效合成风速曲线,为后续研究风速变化下的能源产出结果提供风速数据。
风力发电系统中,风力通过风力发电机的转动来驱动发电机产生电能。转动惯量对风力发电系统的响应速度、稳定性和功率输出等方面产生影响。因此,利用本文模型构建船舶动力系统的传动系统模型,得到高速端与低速端的转动惯量,高速端与低速端的转动惯量如图2所示。根据图1和图2可知,本文模型可有效得到船舶动力系统中传动系统的高速端与低速端的转动惯量,且高端与低速端转动惯量的变化趋势基本一致。不同风速类型下,传动系统高速端的转动惯量,均高于低速端的转动惯量。当风速变化时,船舶动力系统中的转动惯量也随之发生改变。随着风速的增加,高速端与低速端的转动惯量也出现增加的趋势。这是由于较高的风速可以产生更大的风力,使得转动惯量对叶片负载的影响更加明显。当风速增大时,风力对叶片的作用力也增大,需要更大的转矩去抵消叶片受到的风力,使得转动惯量对转矩需求的影响更加显著。而图2中,高速端在15~24 h时出现了与风速不完全一致的波动。这是由于风速出现下降,低风速不利于改善系统的旋转惯性,容易因突变风速而引起振荡现象,影响系统的稳定性。
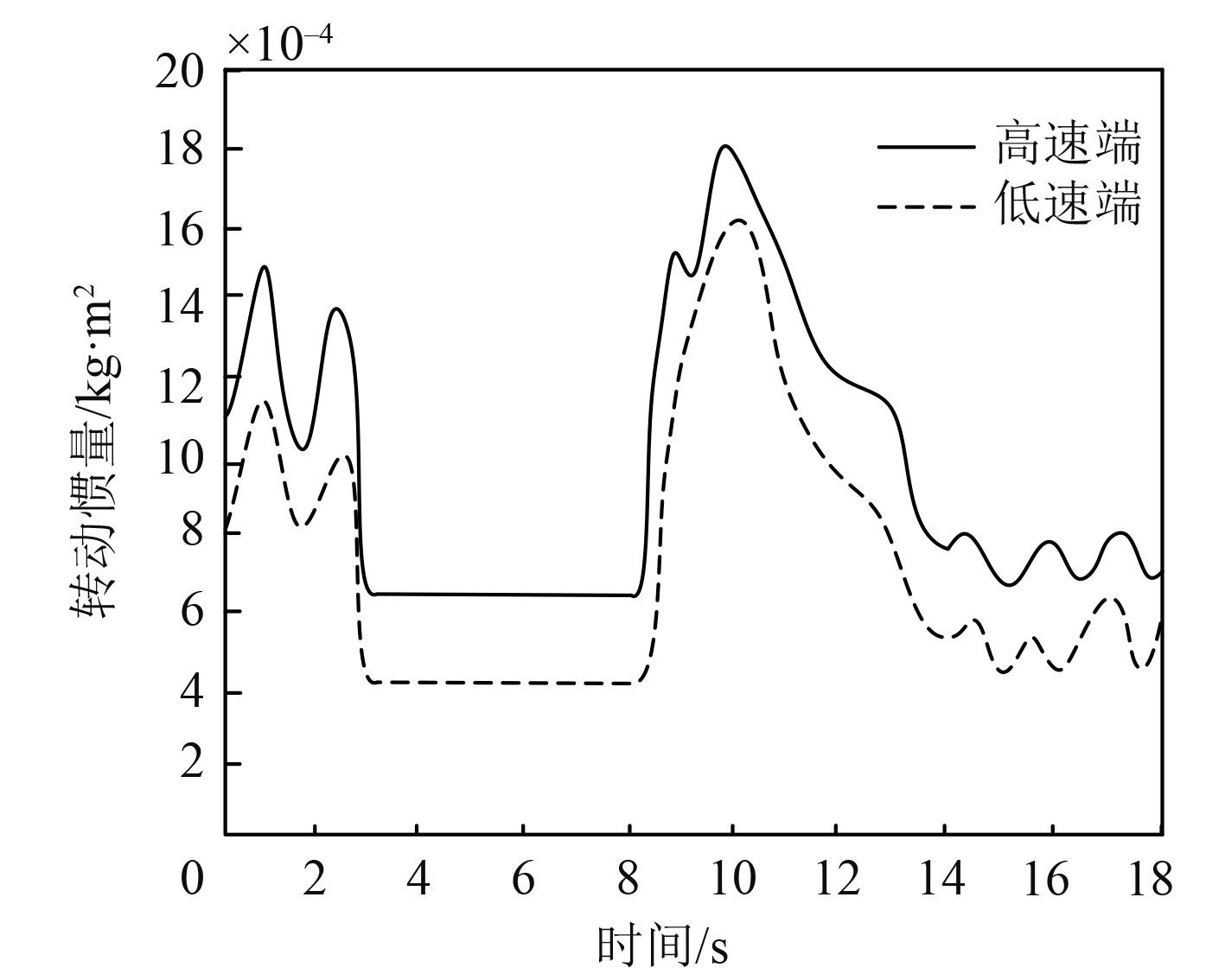
|
图 2 高速端与低速端的转动惯量 Fig. 2 Moment of inertia at high speed and low speed |
对于风力发电系统来说,能源产出通常指的是通过转化风能而获得的电能产出量。因此在风速扰动下,利用本文模型构建自动化风力发电模型,得到该船舶动力系统单个发电机组的电能产出量结果如图3所示。根据图1和图3可知,本文模型可有效得到自动化风力发电的电能产出量。该船舶动力系统自动化电能产出量随风速的增大而提升,最高风速时,自动化风力发电功率最大,在21.86 kW左右,最低风速时自动化风力发电功率最小,在20.62 kW左右。实验证明,本文模型可有效得到风速扰动下的电能产出量,且风速越大,能源产出越大,有助于确定系统的利用率。
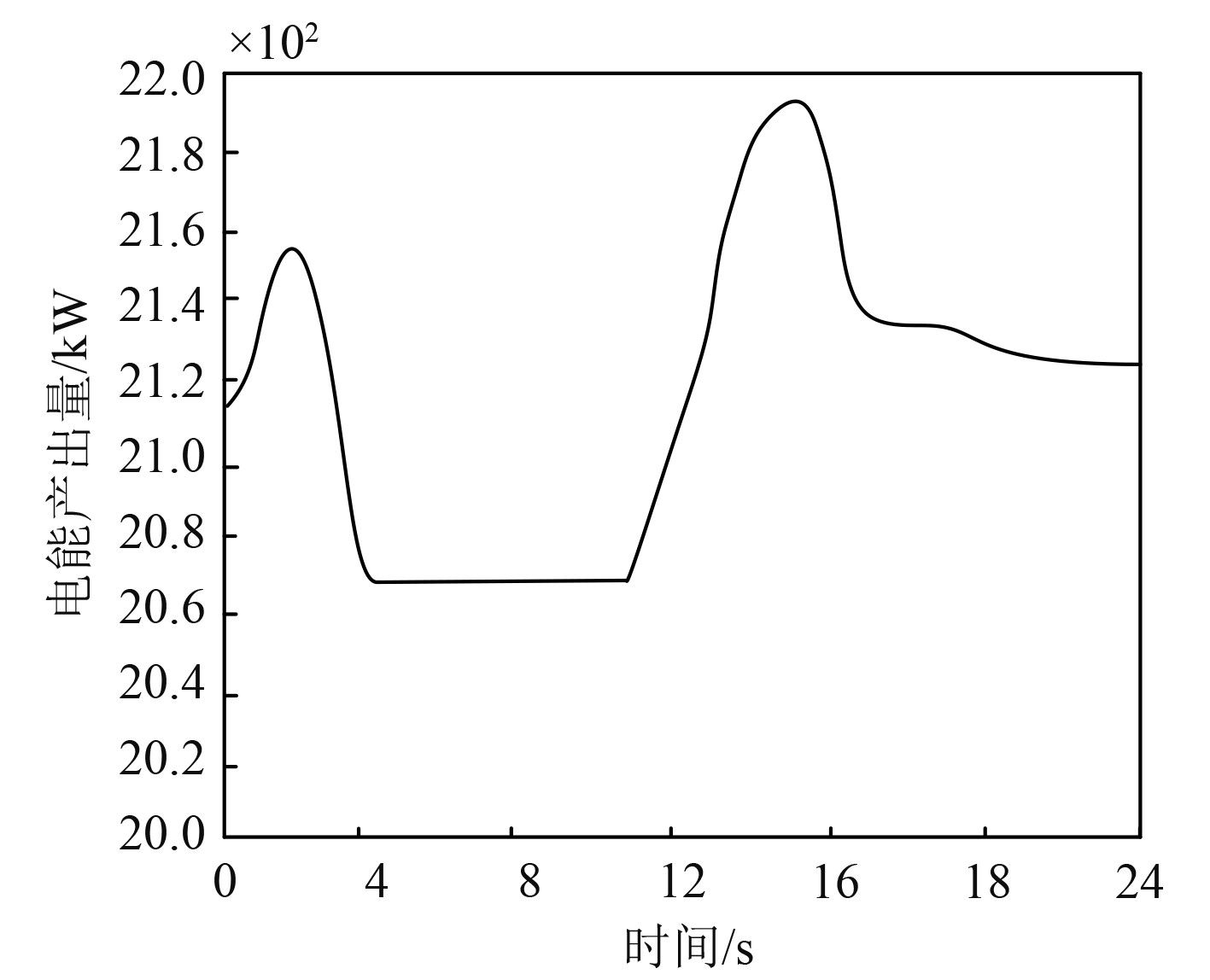
|
图 3 自动化风力发电的功率响应特性 Fig. 3 Power response characteristics of automated wind power generation |
风能属于清洁的可再生能源,可有效缓解环境污染问题,在船舶发电领域中应用越来越多。但其发电稳定性较差,为此构建船舶动力系统自动化风力发电模型,得到高速端与低速端的转动惯量以及风速扰动下的电能产出量,为提升风力发电稳定性提供参考。
| [1] |
杨元龙, 孙玲, 张晓滨, 等. 基于数字孪生的舰船蒸汽动力总体模型框架研究[J]. 中国舰船研究, 2021, 16(2): 157-167. YANG Yuanlong, SUN Ling, ZHANG Xiaobin, et al. Analysis on the overall model framework of ship steam power based on digital twin[J]. Chinese Journal of Ship Research, 2021, 16(2): 157-167. DOI:10.19693/j.issn.1673-3185.01884 |
| [2] |
周少伟, 吴炜, 张涛, 等. 舰船动力系统数字孪生技术体系研究[J]. 中国舰船研究, 2021, 16(2): 151-156. ZHOU Shaowei, WU Wei, ZHANG Tao, et al. Digital twin technical system for marine power systems[J]. Chinese Journal of Ship Research, 2021, 16(2): 151-156. |
| [3] |
张惊朝, 戴靠山, 施袁锋. 基于状态空间模型的大型风力机运行模态及不确定性分析[J]. 结构工程师, 2022, 38(1): 14-23. ZHANG Jingzhao, DAI Kaoshan, SHI Yuanfeng. Operational modal analysis with uncertainty quantification using state-space model for large-scale wind turbines[J]. Structural Engineers, 2022, 38(1): 14-23. |
| [4] |
宋子秋, 刘吉臻, 胡阳, 等. 考虑冰载荷的近海固定桩风电机组运行特性建模与分析[J]. 中国电机工程学报, 2021, 41(12): 4144-4153. SONG Ziqiu, LIU Jizhen, HU Yang, et al. Modeling and analysis of bottom fixed platform offshore wind turbine under ice loads[J]. Proceedings of the CSEE, 2021, 41(12): 4144-4153. |
| [5] |
季一润, 槐青, 袁茜, 等. 基于虚拟同步型风力发电机组的风电场动态聚合模型研究[J]. 电力系统及其自动化学报, 2023, 35(2): 37-44. JI Yirun, HUAI Qing, YUAN Qian, et al. Dynamic aggregation model of wind farm based on VSG wind turbines[J]. Proceedings of the CSU-EPSA, 2023, 35(2): 37-44. |
| [6] |
陈婕, 张怡, 房方, 等. 基于仿射扰动反馈的风力发电机组多目标随机模型预测控制[J]. 中国电机工程学报, 2023, 43(2): 496-507. CHEN Jie, ZHANG Yi, FANG Fang, et al. Affine-disturbance-feedback-based multi-objective stochastic model predictive control of wind turbine[J]. Proceedings of the CSEE, 2023, 43(2): 496-507. |
 2023, Vol. 45
2023, Vol. 45
