2. 上海外高桥造船海洋工程有限公司 生产管理部,上海 200131
2. Production management department, Shanghai Waigaoqiao Shipbuilding and Offshore Engineering Co., Ltd, Shanghai 200131, China
浮式钻井生产储卸油装置(Floating Drilling Production Storage and Offloading System,FDPSO),即在FPSO的基础上增加钻井功能,是集海上油气处理、储油和卸油、发电、供热、控制、生活功能为一体的浮式容器状生产系统,具有初期投资小、建造周期短、储油能力强、适应水深范围广、迁移方便、可重复使用等多方面优点,并广泛适用于深海、浅海及边际油田[1]。我国目前已经开发或即将开发的海上油气田,大部分属于边际油田的范畴。因此,FDPSO比较适用于我国目前的海上油气田开发。经过长期发展,出现多种新型式FDPSO,包括深水八角形FDPSO、沙漏式FDPSO、多筒式FDPSO、圆筒式FDPSO。通过对圆筒型FDPSO进行运动响应分析可知,圆筒型FDPSO既存在投资小、成本低、周期短等优势也存在些许不足,如圆筒型FDPSO的垂荡运动幅度较大。
为了研究开发出具有国际先进水平的FDPSO总体方案,王世圣等[2]开展了深水八角形FDPSO的概念设计研究,分析了不同尺寸的垂荡板对八角形FDPSO固有特性的影响以及不同浮体直径对浮体运动性能的影响。研究结果表明,垂荡板尺寸的增加,对浮体固有周期的改变非常明显。赵志娟[3]针对船型FPSO耐波性差的特点,结合目前已有的新概念浮式生产装置的优势,从浮式生产装置的外形和功能上进行创新,设计了一种适合在我国南海进行作业的新型多筒式FDPSO。经过计算分析可知,多筒式FDPSO的固有周期能远离其波浪周期。姚宇鑫[4]提出一种新型沙漏式浮式生产储油系统,分析了垂荡运动响应及黏性阻尼和非线性刚度对沙漏型浮体垂荡运动性能的影响,为新型浮式生产装置的主浮体外形设计提供了参考依据和准则。刘利琴[5]延用SEVEN型FPSO的外形,但改变了垂荡板的结构,去除了筒体和垂荡板相连部分的坡脚,加装有倾斜角度的垂荡板,研究不同海况下垂荡板倾斜角度的变化对其阻尼特性及减摇效果的影响。研究发现,锥角越小对结构垂荡运动的抑制效果越好,不同海况下10°锥角能较好抑制结构的纵摇运动。
由于圆筒型FDPSO较差的垂荡性能会导致其作业过程受到严重影响,本文针对加装了延伸筒体和箱型减动结构的圆筒型FDPSO,开展不同高度和不同宽度的减动结构条件下圆筒型FDPSO垂荡运动的CFD数值模拟分析。根据数值模拟得到的FDPSO垂荡运动和垂向受力时历曲线,分析减动结构宽带和高度对垂荡运动的影响。根据数值模拟得到的流场信息,阐明减动结构尺寸影响FDPSO垂荡运动的物理机制。
1 数学模型和数值方法 1.1 不可压缩粘性流体的控制方程在本文的数值模拟研究中,浮式钻井生产储卸油装置垂荡运动的水动力载荷通过求解装置外部不可压缩粘性流体来获得。三维条件下,对于均质不可压缩流体,流体的密度在运动过程中保持不变,则三维不可压缩粘性流体的
| $ \mathrm{d}\mathrm{i}\mathrm{v}\mathit{v}=0 ,$ | (1) |
| $ \mathrm{\rho }\frac{{\rm{D}}v}{{\rm{D}}t}=\rho {\mathit{F}}_{b}-gradp+\mathrm{\mu }{\nabla }^{2}v。$ | (2) |
式中:
本文数值模拟涉及水和空气两相流的研究,采用欧拉-欧拉模型(Euler-Euler model)描述计算域内的两相流体,并采用VOF方法且引入相体积分数
VOF模型的分数函数为:
| $ \left\{ \begin{aligned} &\alpha = 0 \quad {\text{air}} ,\\ & 0 < \alpha < 1 \quad {\text{interface}} ,\\ & \alpha = 1 \quad {\text{water}} 。\end{aligned} \right. $ | (3) |
VOF模型函数的输运方程遵循的对流方程为:
| $ \frac{\partial \alpha }{\partial t}+\nabla \cdot \left({\boldsymbol{U}}\alpha \right)+\nabla \cdot \left({{\boldsymbol{U}}}_{\mathrm{r}}\left(1-\alpha \right)\alpha \right)=0 。$ | (4) |
其中,
上述连续性方程和动量方程中的密度和粘度是通过对两相流体所占比例加权平均后得到的,函数如下:
| $ \mathrm{\rho }=\mathrm{\alpha }{\rho }_{w}+(1-\mathrm{\alpha }){\rho }_{a},$ | (5) |
| $ \mathrm{\mu }={\alpha \mu }_{w}+(1-\alpha ){\mu }_{a}。$ | (6) |
式中,下标
采用由北海海浪联合计划测量分析得到的JONSWAP谱描述不规则波[7]。波浪参数的设置如表1所示。
|
|
表 1 波浪参数 Tab.1 Wave parameters |
在CFD数值模拟研究中,浮体在流体中运动的求解至关重要。在只考虑浮体单自由度运动的情况下,可基于达朗贝尔原理的直接平衡法建立FDPSO的运动方程:
| $ m\ddot{y}+\mathrm{c}\dot{y}+ky={F} 。$ | (7) |
其中:m为浮体的质量;y为浮体在运动方向上的位移;c为粘滞阻尼系数;k为刚度系数;F为浮体在运动方向所受的激励力。
当FDPSO做垂荡运动时,力F由水动力
| $ {F}={F}_{v}+{F}_{a} ,$ | (8) |
| $ {F}_{a}=-{m}_{a}\ddot{y} 。$ | (9) |
将式(8)和式(9)代入式(7)中,可得到FDPSO垂荡运动方程:
| $ (m+{m}_{a})\ddot{y}+\mathrm{c}\dot{y}+ky={F}_{v} ,$ | (10) |
而FDPSO的固有周期为:
| $ T=\frac{1}{f}=2 \text{π} \sqrt{\frac{m+{m}_{a}}{k}} 。$ | (11) |
为了减小FDPSO的垂荡性能,可以通过增加结构附加质量的方法增大平台垂荡固有周期,使平台垂荡运动固有周期远离其波浪周期。
2 物理模型以表2中的平台实际尺寸按照1∶77.8的缩尺比建立模型,基于SolidWorks建立的平台三维几何模型剖面图如图1所示。
|
|
表 2 物理参数 Tab.2 Physical parameters |
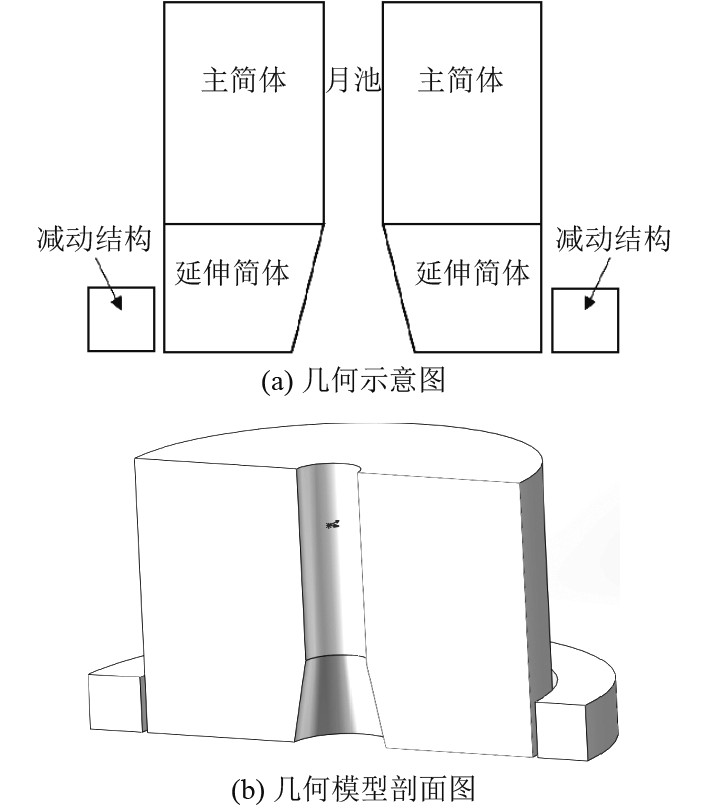
|
图 1 几何模型示意图 Fig. 1 Schematic diagram of the geometric model |
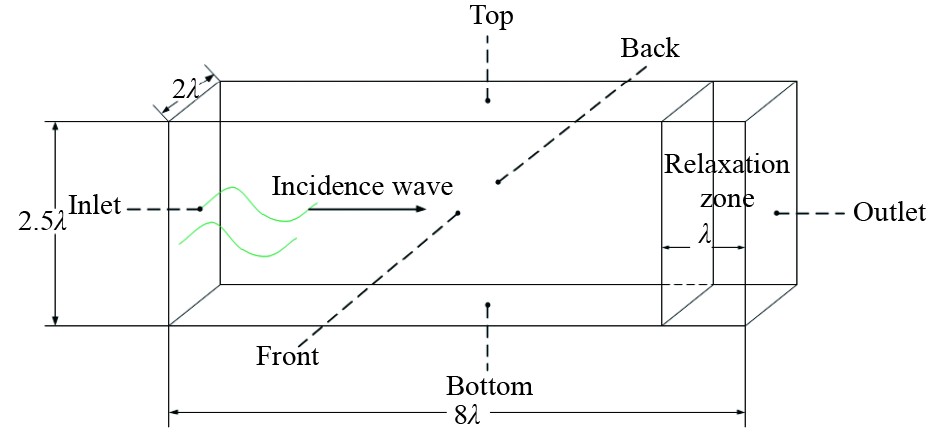
本文所用模型为轴对称结构,故取一半模型进行计算域设置和网格划分。计算域的尺寸为
|
图 2 计算域草图 Fig. 2 Computational domain sketch |

|
图 3 流体网格 Fig. 3 Fluid mesh |
为了对网格数量进行收敛性分析,本文考虑在静水中的垂荡衰减情况[8],针对有间隙减动结构宽度和高度均为10 m时生成3种不同数量的网格。按照网格数量的不同分为网格1、网格2、网格3,如表3所示。
|
|
表 3 圆筒型FDPSO算例网格收敛性验证数值 Tab.3 Mesh convergence verification numerical value of cylindrical FDPSO example |
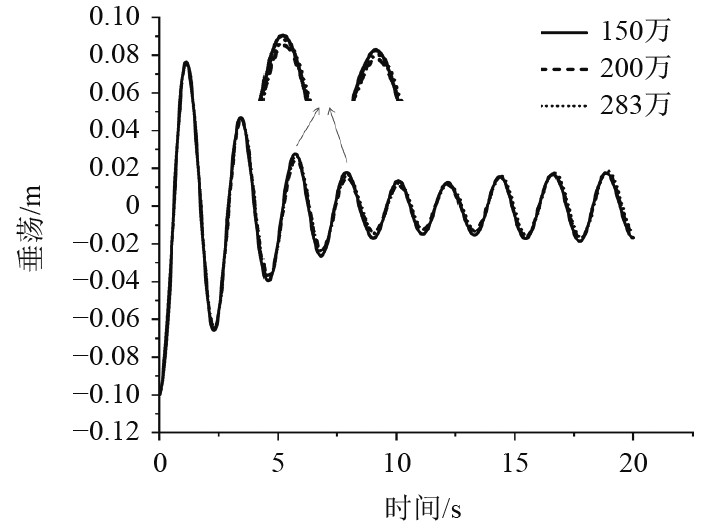
分别采用150万、200万、283万3种不同网格密度模型计算垂荡自由衰减曲线,如图4所示。
|
图 4 不同网格密度模型垂荡自由衰减曲线 Fig. 4 Heave free attenuation motion curve of models with different mesh densities |
可以看出,网格数量增加使网格精细度也随之增加,采用200万网格数与采用283万网格数所得的计算结果基本吻合,而150万网格数的计算结果有些许误差。同时考虑计算效率,后续使用200万网格数进行计算。
3.3 结果分析本文所采用的圆筒型FDPSO带有延伸筒体与减动结构,在只考虑浮式生产装置垂荡运动的情况下,进行减动结构尺寸变化对圆筒型浮式生产装置垂荡运动抑制敏感性分析。首先,固定减动结构高度(10 m),对减动结构宽度10~15m之间取值(10、11、12、13、14、15 m),开展多工况数值算例;另外,固定减动结构宽度(10 m),对减动结构高度10~15 m之间取值(10、11、12、13、14、15 m),开展多工况数值算例,不同减动结构尺寸下FDPSO的排水量见表4。
|
|
表 4 减动结构各个尺寸模型排水重量 Tab.4 Drainage weight of each size model of anti-motion structure |
通过对减动结构宽度为10、11、12、13、14、15 m的模型垂荡运动进行数值模拟,得到其垂荡时历曲线。图5为宽度10、12、15的模型的垂荡运动时历曲线。取

|
图 5 不同减动结构宽度垂荡时历曲线 Fig. 5 Heave time history curves of different |
对不同减动结构宽度垂荡时历曲线进行统计,可以得到不同减动结构宽度模型的垂荡固有周期,如表5所示。根据缩尺比换算得到实尺度平台运动的固有周期。减动结构宽度为10 m时,其垂荡固有周期为17.91 s;宽度为11 m时固有周期为18.79 s;宽度为12 m时固有周期为20.11 s;宽度为13 m时固有周期为21.34 s。表5数据表明,减动结构宽度的增加使圆筒型FDPSO垂荡运动的固有周期增大。相比于减动结构宽度为10 m的模型,其他几种宽度的模型的固有周期分别增加4.93%、12.32%、19.21%。
|
|
表 5 不同减动结构宽度的垂荡固有周期 Tab.5 Heave natural period of different anti-motion structure width |
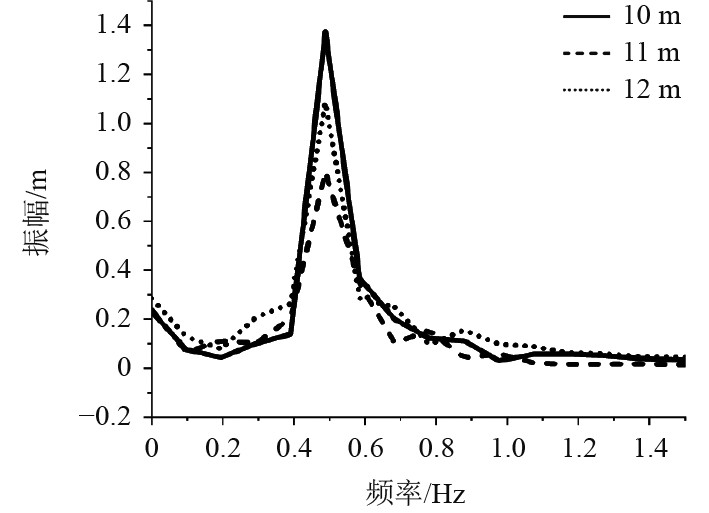
|
图 6 不同减动结构宽度运动幅值 Fig. 6 Heave time history curves of different |
表6比较了减动结构宽10 m和宽15 m的垂荡运动的最大值与最小值。可知,在只考虑浮体垂荡运动的情况下,当减动结构宽度从10 m增加为15 m时,浮体的垂向受力幅值有所减小,减小了平台的垂荡运动,减动结构宽度为15 m的平台的垂荡运动较结构宽度为10 m的平台降低了47.7%。
|
|
表 6 宽10 m和宽15 m垂荡运动比较 Tab.6 Comparison of heave motion between 10 m and 15 m width |
采用CFD方法对浮体垂荡运动进行数值模拟。减动结构高度不变(10 m),宽度为11 m和14 m的模型在第5个运动周期内的涡量图如图7所示。由图7可知,浮体在运动过程中,减动结构和延伸筒体的边缘尖角处以及间隙中产生旋涡。当FDPSO从平衡位置向下运动至最低位置时(5~5.25T),减动结构顶部尖角处产生方向向上的旋涡,减动结构底部尖角处产生的旋涡在浮体底部形成堆积,间隙处的旋涡向上运动;当FDPSO从最低位置向上运动至平衡位置时(5.25~5.5T),向上运动的过程中,旋涡逐渐开始脱落,减动结构上方尖角处脱落的旋涡逐渐在减动结构上方堆积,减动结构下方尖角处脱落的旋涡向后方运动,减动结构尖角处和间隙处随及产生新的旋涡;当FDPSO从平衡位置向上运动至更高位置时(5.5~5.75T),减动结构外侧尖角处产生方向向下的旋涡;当FDPSO从最高位置向下运动至平衡位置时(5.75~6.0T),减动结构尖角处产生方向向上的旋涡,并随着时间增加旋涡逐渐脱落。前期脱落的旋涡继续远离圆筒型FDPSO,并逐渐消散在周围流场中。整体而言,运动过程中由边缘尖角和间隙处产生的涡旋结构呈现向周围流场耗散传播的趋势[8]。宽度大的模型涡量的产生与耗散相较于宽度小的模型有所增加。

|
图 7 不同宽度减动结构模型涡量分布 Fig. 7 The vortex field distribution of different anti-motion structure width |
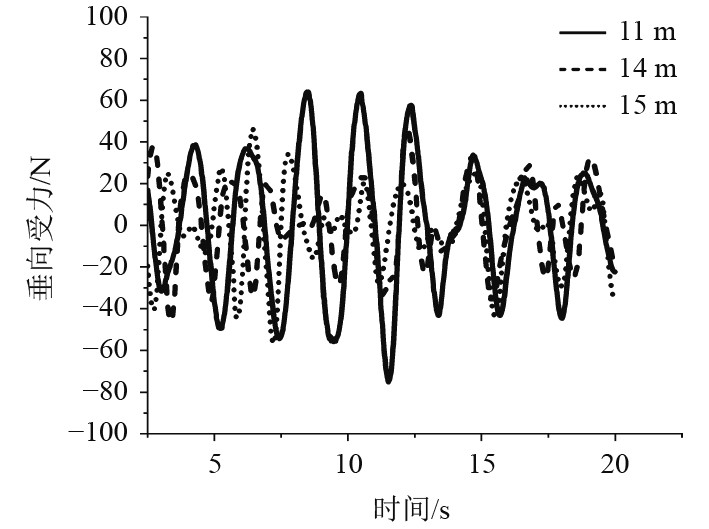
图8为不同减动结构宽度模型垂向受力的时历曲线。在研究过程中考虑流体粘性的作用,液体的粘性会对运动中的物体产生阻力,即粘压阻力,相对运动会使减动结构前后形成压力差,减动结构宽度的增加,会使前后的粘性压差逐渐增大,从而使得粘性引起的摩擦阻力发生变化,而使浮式生产装置的垂向受力幅值有所减小。
|
图 8 不同减动结构宽度垂向受力时历曲线 Fig. 8 Time-history curves of vertical force with different width of anti-motion structure |
综上所述,圆筒型FDPSO减动结构宽度的增加,增大了结构垂荡运动固有周期,使其远离波浪主能量周期范围,能够有效减缓平台的垂荡运动。
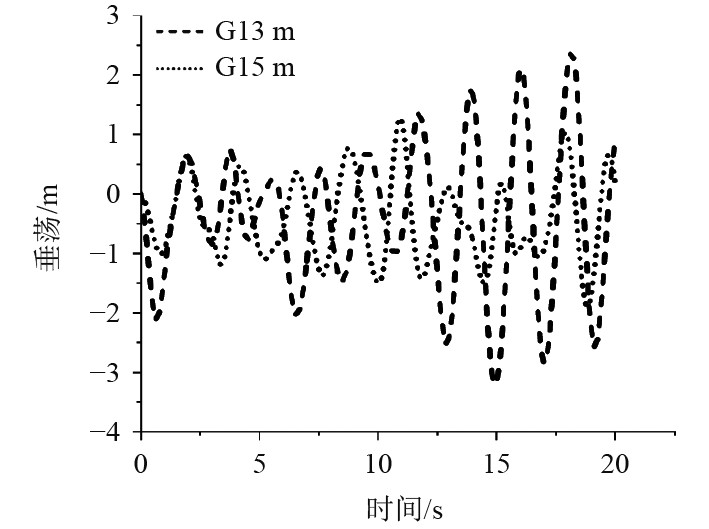
3.3.2 减动结构高度对模型垂荡运动的影响通过对减动结构高度为10、11、12、13、14、15 m的模型垂荡运动进行数值模拟,得到其垂荡时历曲线,图9为高度13、15 m模型的垂荡运动时历曲线。取
|
图 9 不同减动结构高度垂荡时历曲线 Fig. 9 Heave time history curves of different |
|
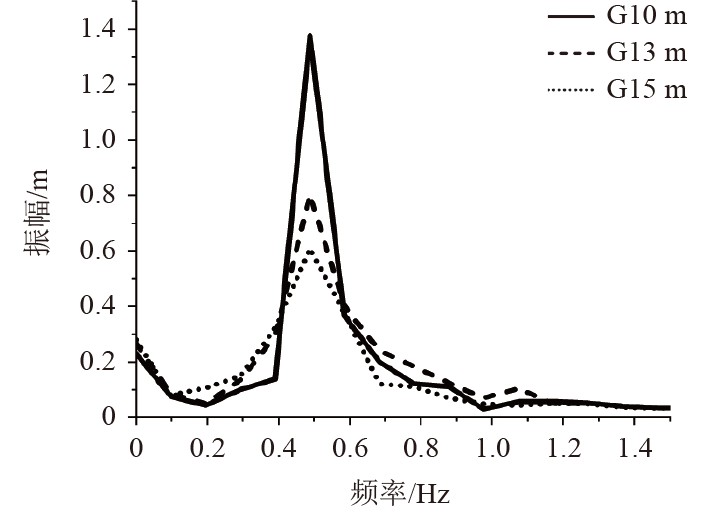
图 10 不同减动结构高度运动幅值 Fig. 10 Heave time history curves of different |
对不同减动结构高度垂荡时历曲线进行统计,可以得到不同减动结构高度模型的垂荡固有周期,如表7所示。根据缩尺比换算得到实尺度平台运动的固有周期。减动结构高度为10 m时,其垂荡固有周期为17.91 s;高度为13 m时,固有周期为18.52 s;高度为15 m时,固有周期为19.23 s。表7数据表明,减动结构高度的增加使圆筒型FDPSO垂荡运动的固有周期增大。相比于减动结构高度为10 m的模型,其他几种高度模型的固有周期分别增加3.45%、7.93%。
|
|
表 7 不同减动结构高度的垂荡固有周期 Tab.7 Heave natural period of different anti-motion structure height |
表8比较了减动结构高13 m和高15 m的垂荡运动的最大值与最小值。可知,在只考虑浮体垂荡运动的情况下,当减动结构高度从13 m增加为15 m时,浮体的垂向受力幅值有所减小,减小了平台的垂荡运动,减动结构高度为15 m的平台的垂荡运动较结构高度为13 m的平台降低了43.1%。
|
|
表 8 高13 m和高15 m垂荡运动比较 Tab.8 Comparison of heave motion between 13 m and 15 m heights |
减动结构宽度不变(10 m)、高度为12 m和15 m的模型在第6个运动周期内的涡量图如图11所示。可知,浮体在运动过程中,减动结构和延伸筒体的边缘尖角处以及间隙中产生旋涡。当FDPSO从平衡位置向下运动至最低位置时(6~6.25T),减动结构顶部尖角处产生方向向上的旋涡,减动结构底部尖角处产生的旋涡在浮体底部形成堆积,间隙处的旋涡向上运动;当FDPSO从最低位置向上运动至平衡位置时(6.25~6.5T),向上运动的过程中,旋涡逐渐开始脱落,减动结构上方尖角处脱落的旋涡逐渐在减动结构上方堆积,减动结构下方尖角处脱落的旋涡向后方运动,减动结构尖角处和间隙处随及产生新的旋涡;当FDPSO从平衡位置向上运动至更高位置时(6.5~6.75T),减动结构外侧尖角处产生方向向下的旋涡;当FDPSO从最高位置向下运动至平衡位置时(6.75~7.0T),减动结构尖角处产生方向向上的旋涡,并随着时间增加旋涡逐渐脱落。前期脱落的旋涡继续远离圆筒型FDPSO,并逐渐消散在周围流场中。整体而言,运动过程中由边缘尖角和间隙处产生的涡旋结构呈现向周围流场耗散传播的趋势。高度增加引起的涡量的产生与耗散有所增加,但相比宽度增加所引起的涡量变化不明显。

|
图 11 不同高度减动结构模型涡量分布 Fig. 11 The vortex field distribution of different anti-motion structure height |
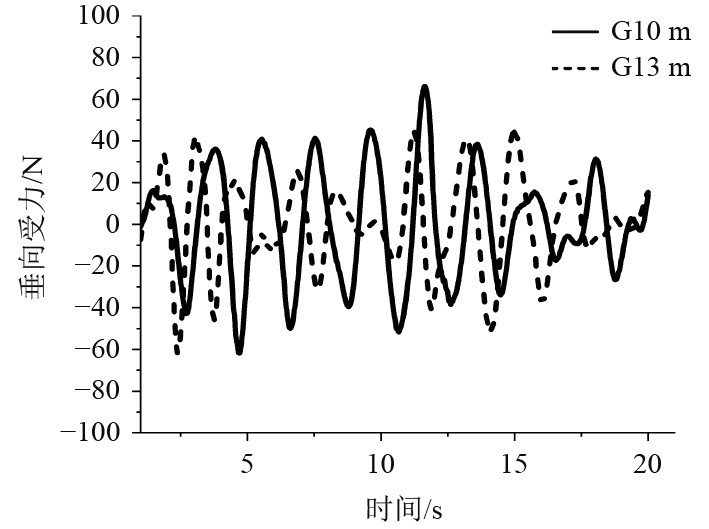
图12为不同减动结构高度模型垂向受力的时历曲线。本文在研究过程中考虑流体粘性的作用,液体的粘性会对运动中的物体产生阻力,即粘压阻力,相对运动会使减动结构前后形成压力差,减动结构宽度的增加,会使前后的粘性压差逐渐增大,从而使得粘性引起的摩擦阻力发生变化,而使浮式生产装置的垂向受力幅值有所减小,但减动结构高度变化对其前后粘性压差影响较小。
|
图 12 不同减动结构高度垂向受力时历曲线 Fig. 12 Time-history curves of vertical force with different height of anti-motion structure |
综上所述,圆筒型FDPSO减动结构高度的增加,能够增大结构垂荡运动固有周期,但较其宽度增加所引起的固有周期的增大幅度来讲,其高度增加所引起的固有周期增大幅度较小。
4 结 语本文采用计算流体力学软件STAR-CCM+对带不同宽度减动结构和不同高度减动结构的新型圆筒型FDPSO在不规则波作用下的垂荡运动进行数值模拟。根据计算结果,得出如下结论:
1)在固定减动结构高度的情况下,增加减动结构宽度能够有效增大新型圆筒型FDPSO垂荡运动固有周期,使其远离波浪主能量周期范围,即宽度的增加对浮式生产装置的垂荡运动有抑制作用。
2) 在固定减动结构宽度的情况下,减动结构高度的增加也在一定程度上增大了新型圆筒型FDPSO垂荡运动固有周期,对其垂荡运动有抑制作用。
3)新型圆筒型FDPSO在运动过程中,在延伸筒体与减动结构边缘尖角处产生旋涡,尤其在减动结构与延伸筒体的间隙处产生大量旋涡。
4)带高宽度减动结构模型周围旋涡的产生与脱落相比低宽度减动结构模型有明显增加,导致减动结构摩擦阻力的增加;高度变化引起的旋涡的产生与脱落相比于宽度变化相对较弱,高度的增大导致减动结构摩擦阻力的增加。
| [1] |
王天英, 冯永训. 新概念FPSO最新研究进展[J]. 船海工程, 2011, 40(5): 184-188+192. DOI:10.3963/j.issn.1671-7953.2011.05.052 |
| [2] |
王世圣, 赵晶瑞, 谢彬, 等. 深水八角形FDPSO 总体性能分析[J]. 船海工程, 2014, 43(3): 183-186+189. DOI:10.3963/j.issn.1671-7953.2014.03.045 |
| [3] |
赵志娟. 多筒式FDPSO概念设计及水动力性能研究[D]. 天津: 天津大学, 2012.
|
| [4] |
姚宇鑫, 王文华, 黄一. 新型沙漏式浮体的垂荡运动响应特性分析[J]. 华中科技大学学报(自然科学版), 2015, 43(7): 129–132.
|
| [5] |
刘利琴, 张晓蕊, 唐友刚, 等. 基于CFD方法的FDPSO锥型垂荡板阻尼特性[J]. 中国海洋平台, 2019, 34(3): 25-31. DOI:10.3969/j.issn.1001-4500.2019.03.005 |
| [6] |
郭磊. 基于VOF方法的液舱流动数值模拟[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [7] |
杜一豪, 纪翀, 姜胜超, 等. 不规则波下船舶运动响应特征数值分析[J]. 海洋工程, 2021, 39(3): 31-41. DOI:10.16483/j.issn.1005-9865.2021.03.004 |
| [8] |
白杰, 李焱, 曲志森, 等. 新型圆筒型FPSO垂荡抑制结构优化设计[J]. 海洋工程, 2020, 38(1): 20-29. DOI:10.16483/j.issn.1005-9865.2020.01.003 |
 2023, Vol. 45
2023, Vol. 45
