2. 华中科技大学船舶与海洋工程学院,湖北 武汉 430074;
3. 中国舰船研究设计中心,湖北 武汉 430074
2. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China;
3. China Ship Development and Design Center, Wuhan 430074, China
无人水下航行器(Unmanned Underwater Vehicle, UUV)作为深海探索强有力的工具,在智能水下检测[1]、水下清洗[2]等领域发挥着重要作用。通常,UUV可分为有缆水下航行器(Remote Operated Vehicle, ROV)和自主式水下航行器(Autonomous Underwater Vehicle, AUV)[3]。前者大多为开架式结构,通过一根脐带缆与母船通信、供能,后者由于没有电缆,需要自带能源在水下工作,其工作时间受到能源的限制,因此需考虑回收、能源补给、通信等问题[3]。
为了扩展UUV水下作业的能力,大型UUV携带多台小型AUV协同作业正成为一个重要的研究趋势。AUV在完成一定范围内的作业后,自动回收到作为搭载平台的UUV内。因此,AUV的回收控制是实现大型UUV对AUV的搭载和协同作业的关键技术之一。
高剑等[4]研究了基于航路点的AUV回收控制问题,设计自适应滑模控制器,使得AUV沿着规划的航路点运动到回收器中。然而其仅考虑了固定回收站,且将AUV限制为水平运动。针对AUV移动回收站的回收控制问题,齐贝贝等[5]设计了一种模型预测控制算法,对AUV添加状态约束、输入约束,基于模型设计预测控制器实现了AUV水平面内的回坞控制。针对AUV的回收路径控制,潘伟等[6]通过将AUV的运动模型解耦,简化为水平模型、垂直模型,并分别设计模糊滑模、S面控制器,并对其进行了试验仿真验证。Ye等[7]设计了基于视觉的AUV对接系统。其在对接站上安装LED灯,于AUV头部搭载双目摄像头,通过视觉定位方法完成了对AUV的引导。其设计的控制器通过模糊算法自适应调整,水池试验验证其对接成功率大于80%。
上述方法大多都仅考虑AUV的水平回收控制,亦或者回收站静止的情况,但在实际情况中,回收站通常是运动的,且与AUV不在同一个水平面上。因此本文在UUV运动的情况下,基于模型和反步法,设计一种三维运动跟踪控制,解决AUV的回收控制问题。与上述大多数路径跟踪问题不同,本文考虑的是AUV三维轨迹跟踪与母平台运动条件下的回收问题,所设计的控制器无需对AUV模型解耦。可用于解决超大型UUV在运动条件下对AUV的回收问题。
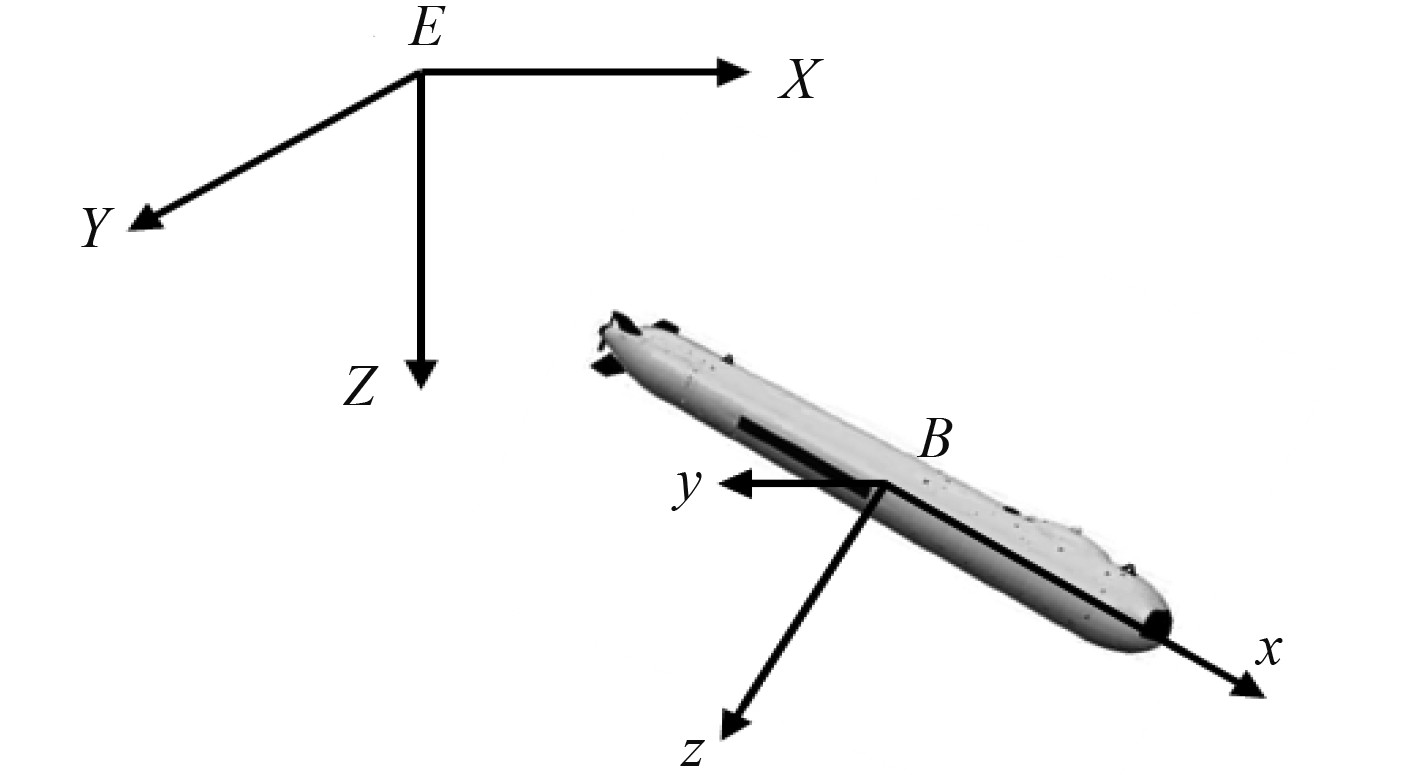
1 运动建模在讨论AUV的运动学问题之前,为方便描述,建立固定坐标系
|
图 1 地球坐标系和随体坐标系 Fig. 1 Earth fixed frame and body fixed frame |
考虑欠驱动AUV运动学模型如下:
| $ \dot {\boldsymbol{\eta}} = {\boldsymbol{J}}({\boldsymbol{\eta}} ){\boldsymbol{\upsilon}},$ | (1) |
| $ {\boldsymbol{J}}({\boldsymbol{\eta}} ) = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{J}}_1}}&{\boldsymbol{O}} \\ {\boldsymbol{O}}&{{{\boldsymbol{J}}_2}} \end{array}} \right],{\dot {\boldsymbol{J}}_1} = {{\boldsymbol{J}}_1}{\boldsymbol{\upsilon}} _2^*,{\boldsymbol{\upsilon}} _2^* = \left[ {\begin{array}{*{20}{c}} 0&{ - r}&q \\ r&0&{ - p} \\ { - q}&p&0 \end{array}} \right] 。$ | (2) |
其中:
| $ {\boldsymbol{M}}\dot {\boldsymbol{v}} + {\boldsymbol{C}}({\boldsymbol{v}}){\boldsymbol{v}} + {\boldsymbol{D}}({\boldsymbol{v}}){\boldsymbol{v}} + {\boldsymbol{G}}({\boldsymbol{\eta}} ) + {{\boldsymbol{\tau}} _d} = {\boldsymbol{\tau}} 。$ | (3) |
其中:
UUV搭载了水声定位装置、惯导、声学多普勒速度仪(DVL),考虑在其背部配备一个回收笼,上面安装LED灯阵列。AUV上搭载了水声定位装置、惯导、水下摄像头、DVL。水声定位装置、视觉定位可测得AUV相对于UUV的位置信息,视觉和惯导加DVL可获得AUV相对于UUV的欧拉角、速度以及角速度。假设UUV始终在水平面内作直线运动,速度恒定,考虑如下回收场景:
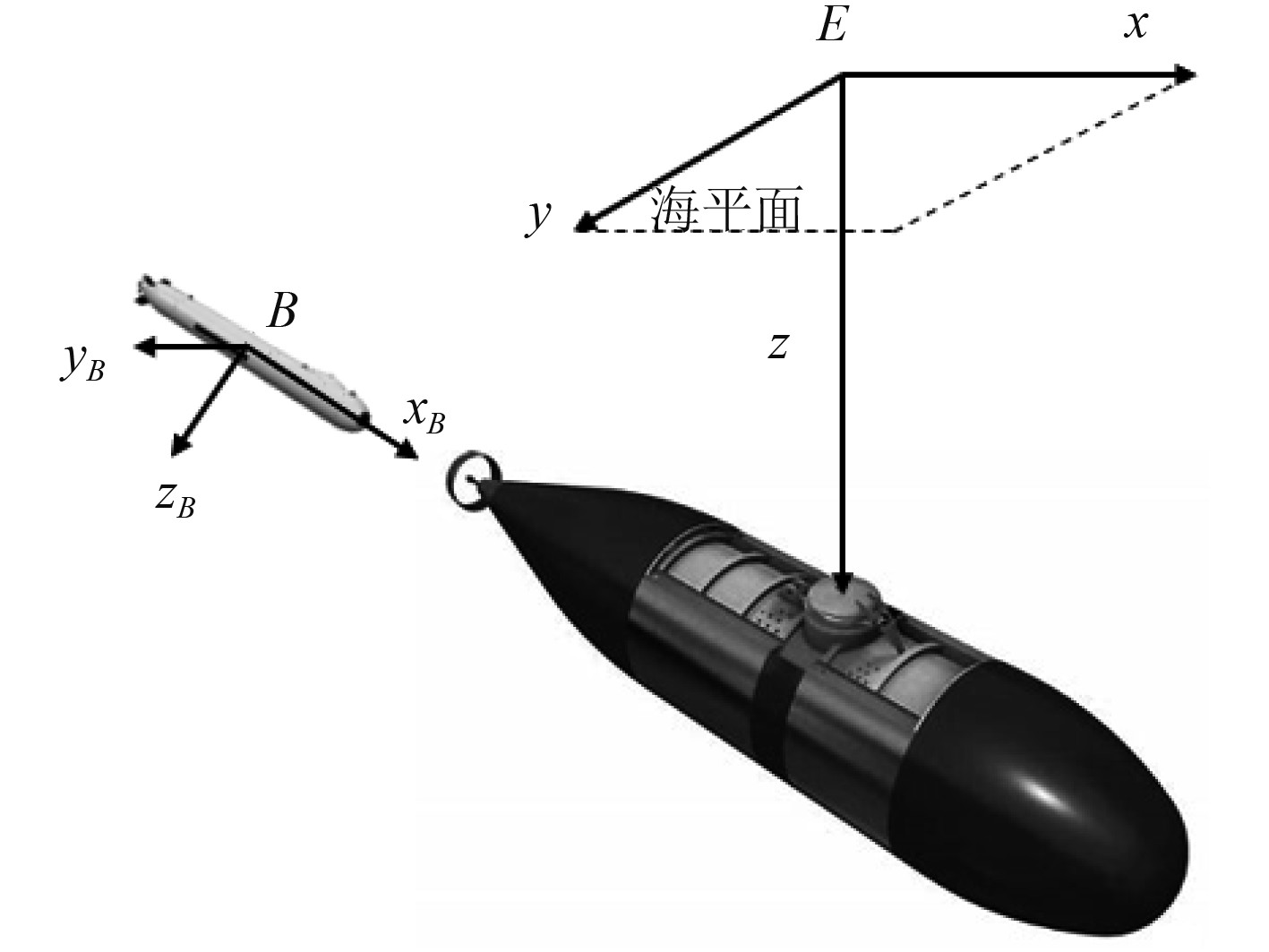
在即将开始进行回收工作时,以UUV竖直方向上海平面上的固定点为
|
图 2 回收坐标系 Fig. 2 Recovery frame |
考虑到水声定位不够精确但应用范围广,而视觉定位精确却范围受限,本文提出如下的回收策略:
1)初对齐
首先定义期望目标点
2)精确回收
进入精确回收阶段,此时期望目标点转变为
针对欠驱动AUV的控制,基于反步法设计控制器[8]。设期望轨迹为
| $ {{\boldsymbol{\eta }}_{1e}} = {{\boldsymbol{\eta}} _1} - {{\boldsymbol{\eta}} _d} ,$ | (4) |
| $ {{\boldsymbol{e}}_\eta } = {\boldsymbol{J}}_1^{\rm{T}}{{\boldsymbol{\eta}} _{1e}} 。$ | (5) |
其中,
| $ {{\boldsymbol{z}}_1} = {{\boldsymbol{e}}_\eta } - {\boldsymbol{\rho}} ,$ | (6) |
对
| $ {\dot {\boldsymbol{z}}_1} = - {\boldsymbol{\upsilon}} _2^*{{\boldsymbol{e}}_\eta } + {\boldsymbol{J}}_1^{\rm{T}}{\dot {\boldsymbol{\eta}} _{1e}} - \dot {\boldsymbol{\rho}},$ | (7) |
结合式(5)~式(7)可得:
| $ {\dot {\boldsymbol{z}}_1} = - {\boldsymbol{\upsilon}} _2^*{{\boldsymbol{z}}_1} + {\boldsymbol{P}}{\left[ {\begin{array}{*{20}{c}} {{u}}&q&r \end{array}} \right]^{\rm{T}}} + {\left[ {\begin{array}{*{20}{c}} 0&v&w \end{array}} \right]^{\rm{T}}} - {\boldsymbol{J}}_1^{\rm{T}}{\dot {\boldsymbol{\eta}} _d} - \dot {\boldsymbol{\rho}} 。$ | (8) |
其中:
| $ {\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&0&{ - \rho } \\ 0&\rho &0 \end{array}} \right] 。$ | (9) |
定义速度误差:
| $ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{v}}} _e} = {\left[ {\begin{array}{*{20}{c}} {{u_e}}&{{q_e}}&{{r_e}} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}} {u - {u_d}}&{q - {q_d}}&{r - {r_d}} \end{array}} \right]^{\rm{T}}} 。$ | (10) |
设计期望速度:
| $ {\left[ {\begin{array}{*{20}{c}} {{u_d}}&{{q_d}}&{{r_d}} \end{array}} \right]^{\rm{T}}} = {{\boldsymbol{P}}^{ - 1}}( - {\boldsymbol{K}}{{\boldsymbol{z}}_1} - {\left[ {\begin{array}{*{20}{c}} 0&v&w \end{array}} \right]^{\rm{T}}} + {\boldsymbol{J}}_1^{\rm{T}}{\dot {\boldsymbol{\eta}} _d} + \dot {\boldsymbol{\rho}} ) ,$ | (11) |
则式(8)可化简为:
| $ {\dot {\boldsymbol{z}}_1} = - {\boldsymbol{\upsilon}} _2^*{z_1} + {\boldsymbol{P}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{v}}} _e} - {\boldsymbol{K}}{{\boldsymbol{z}}_1}。$ | (12) |
设计李雅普诺夫函数为:
| $ {V_1} = \frac{1}{2}{{\boldsymbol{z}}_1}^{\rm{T}}{{\boldsymbol{z}}_1},$ | (13) |
其导数为:
| $ {\dot {\boldsymbol{V}}_1} = {{\boldsymbol{z}}_1}^{\rm{T}}(P{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{v}}} _e} - {\boldsymbol{K}}{{\boldsymbol{z}}_1}) 。$ | (14) |
观察式(14)可知,如果速度误差
令期望速度为:
| $ {{\boldsymbol{v}}_d} = [\begin{array}{*{20}{c}} {{u_d}}&{{\alpha _2}}&{{\alpha _3}}&{{\alpha _4}}&{{q_d}}&{{r_d}} \end{array}]。$ | (15) |
其中:
令
| $ {{\boldsymbol{z}}_2} = {\boldsymbol{v}} - {{\boldsymbol{v}}_d} ,$ | (16) |
设计李雅普诺夫函数为:
| $ {V_2} = \frac{1}{2}{{\boldsymbol{z}}_2}^{\rm{T}}{\boldsymbol{M}}{{\boldsymbol{z}}_2},$ | (17) |
对其求导可得:
| $ {\dot V_2} = {{\boldsymbol{z}}_2}^{\rm{T}}({\boldsymbol{M}}\dot {\boldsymbol{v}} - {\boldsymbol{M}}{\dot {\boldsymbol{v}}_d})。$ | (18) |
结合式(3)和式(18)可得:
| $ {\dot V_2} = {{\boldsymbol{z}}_2}^{\rm{T}}( - {\boldsymbol{C}}({\boldsymbol{v}}){\boldsymbol{v}} - {\boldsymbol{D}}({\boldsymbol{v}}){\boldsymbol{v}} - {\boldsymbol{G}}({\boldsymbol{\eta}} ) - {{\boldsymbol{\tau}} _d} + {\boldsymbol{\tau}} - {\boldsymbol{M}}{\dot {\boldsymbol{v}}_d}) 。$ | (19) |
令
| $ {\boldsymbol{\omega}} = {\boldsymbol{C}}({\boldsymbol{v}}){\boldsymbol{v}} + {\boldsymbol{D}}({\boldsymbol{v}}){\boldsymbol{v}} + {\boldsymbol{G}}({\boldsymbol{\eta}} ) + {{\boldsymbol{\tau }}_d} 。$ | (20) |
式(20)可化简为:
| $ {\dot V_2} = {{\boldsymbol{z}}_2}^{\rm{T}}( - {\boldsymbol{\omega}} + {\boldsymbol{\tau}} - {\boldsymbol{M}}{\dot {\boldsymbol{v}}_d})。$ | (21) |
设计AUV的输入为:
| $ {\tau _i} = {\omega _i} + {M_{ii}}{\dot {\boldsymbol{v}}_{di}} - {c_i}{z_i},i = 1,5,6 。$ | (22) |
令辅助量
| $ {M_{ii}}\dot \alpha = - {\omega _i} + {c_i}{z_i},i = 2,3,4 ,$ | (23) |
则式(21)可化简为:
| $ {\dot V_2} = - {z_2}^{\rm{T}}{\boldsymbol{c}}{{\boldsymbol{z}}_2} 。$ | (24) |
其中:
由上述分析可知,当AUV的输入
为防止输出饱和,对输出进一步处理:
| $ {\boldsymbol{\tau}} = 400\frac{{\boldsymbol{\tau}} }{{{{\left\| {\boldsymbol{\tau}} \right\|}_2}}},{\left\| {\boldsymbol{\tau}} \right\|_2} > 400 。$ | (25) |
该处理降低了误差收敛的速度,对稳定性无影响。
4 仿 真AUV模型参数来源于文献[8],
| $ {{\boldsymbol{\eta}} _d} = \left\{ {\begin{array}{*{20}{c}} {{{[\begin{array}{*{20}{c}} { - 5 + 0.5t}&0&{20}&0&0&0 \end{array}]}^{\rm{T}}},t < 120} ,\\ {{{\boldsymbol{\eta}} _d} = {{[\begin{array}{*{20}{c}} {0.5t}&0&{20}&0&0&0 \end{array}]}^{\rm{T}}},t > 120} 。\end{array}} \right. $ |
AUV的初始状态为:
| $ {\boldsymbol{\eta}} = {[\begin{array}{*{20}{c}} { - 20}&{ - 10}&0&0&0&0 \end{array}]^{\rm{T}}} 。$ |
|
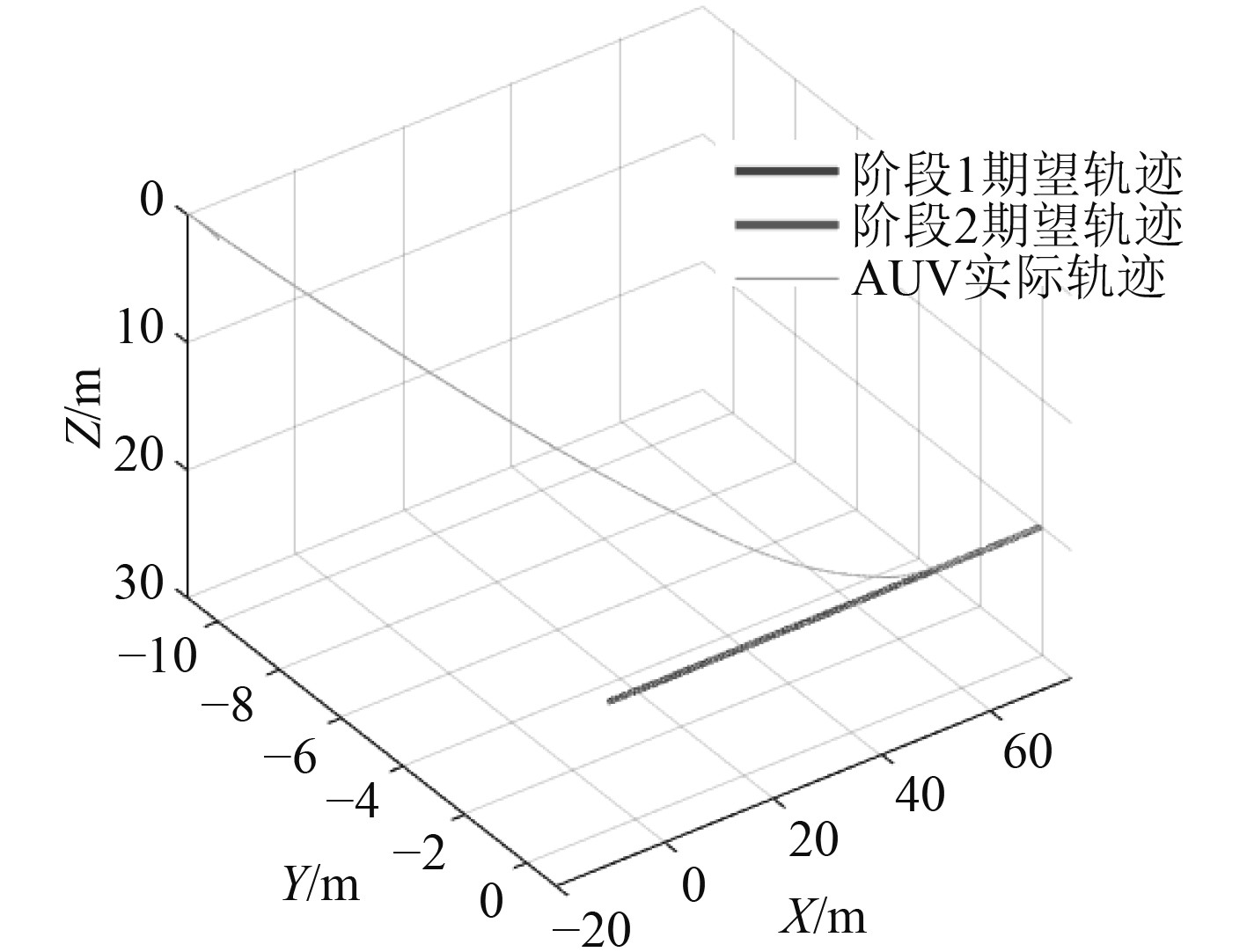
图 3 AUV的三维轨迹运动图 Fig. 3 3D trajectory of AUV |
|
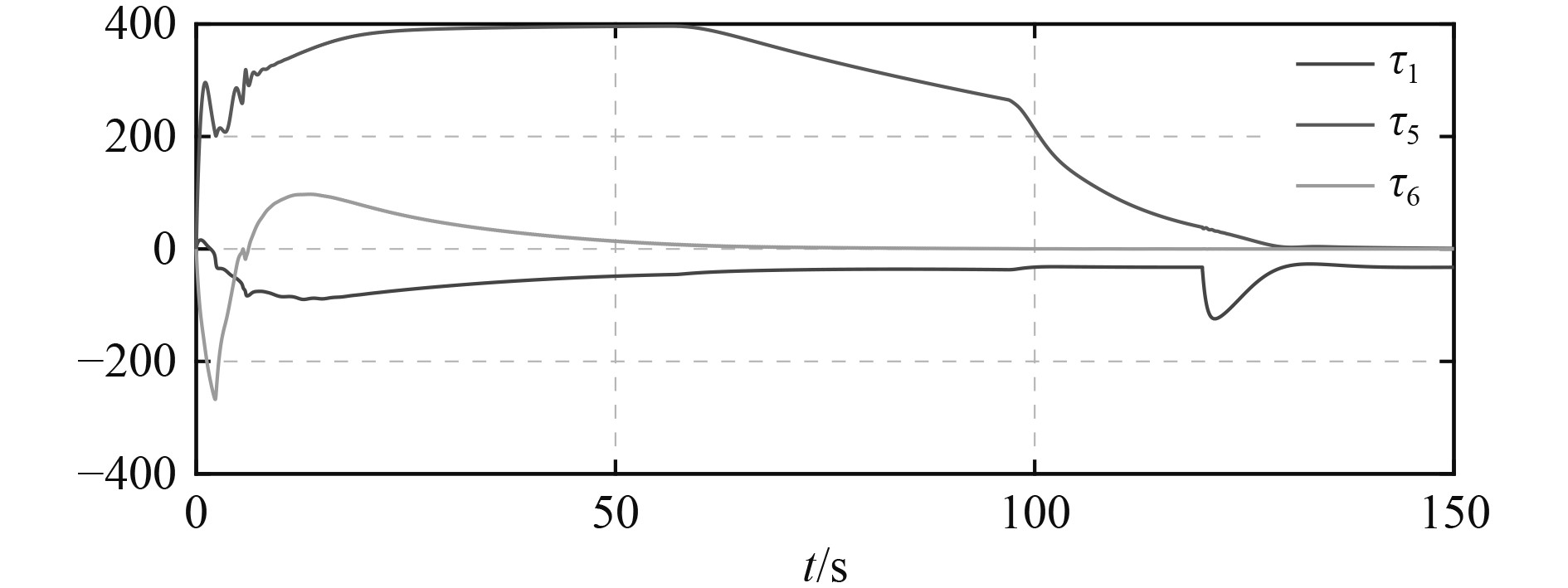
图 6 控制输入 Fig. 6 Inputs of control |
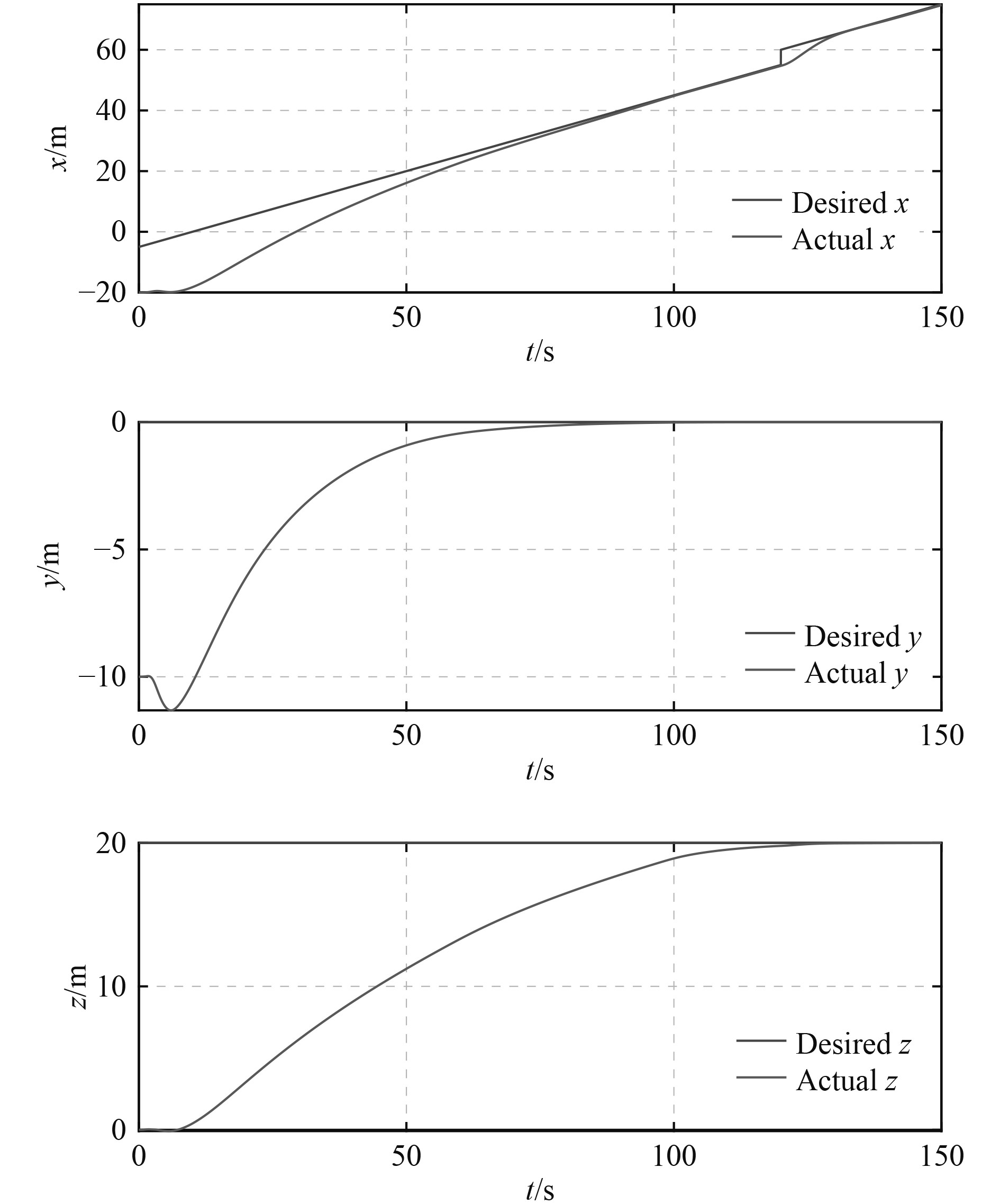
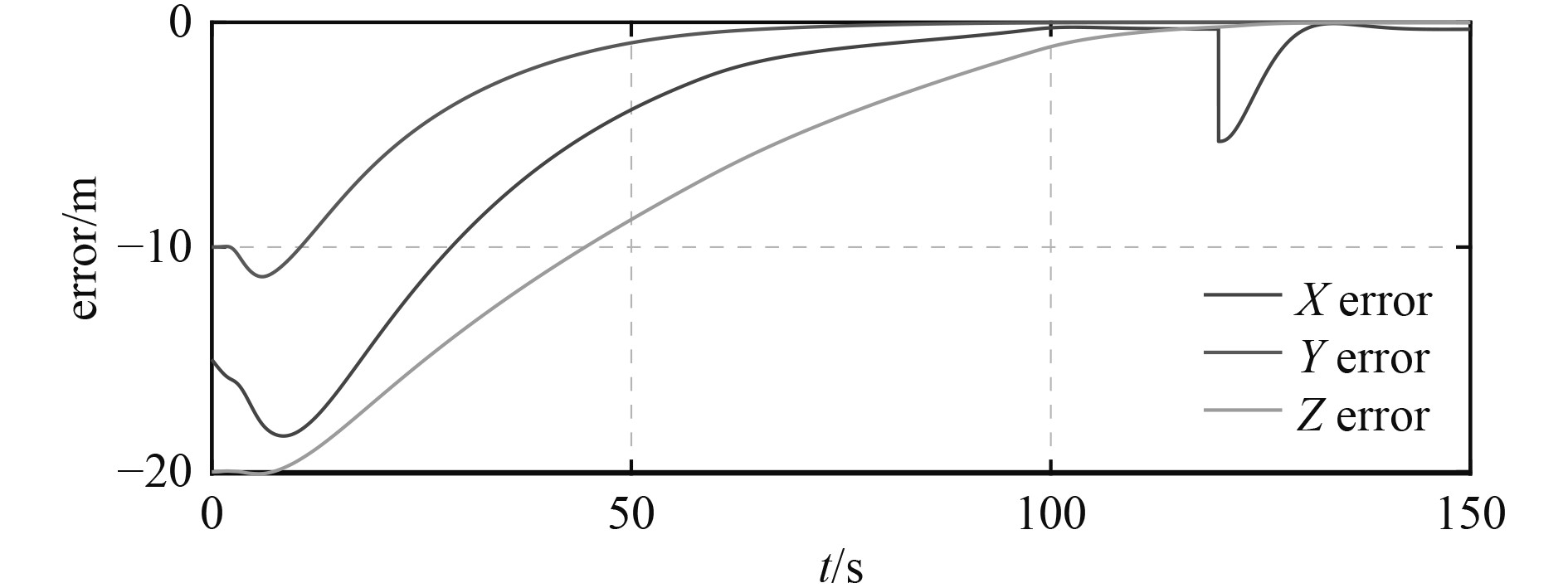
由图3~图6可知,AUV在有着较大初始误差的情况下,跟踪上了作直线运动的UUV。图3给出了AUV的三维轨迹跟踪曲线。AUV首先跟踪上阶段1的期望轨迹,使得AUV与UUV运动于同一条直线上。随后跟踪上阶段2的期望轨迹,完成AUV的回收。图4为期望位置、实际位置的时间曲线,图5为轨迹跟踪误差曲线。可知,位置误差渐进收敛。此外,大约在120 s左右,期望轨迹发生了突变,代表回收过程进入了阶段2,AUV通过大概10 s使误差收敛到0。图6为控制输入,可以看出所设计的控制器较为光滑,易实现。根据上述仿真结果及其分析可知,在考虑了外界海流的情况下,所提出的回收策略、控制器解决了运动回收基站,欠驱动AUV的三维轨迹跟踪回收问题。
|
图 4 期望位置、实际位置的时间曲线 Fig. 4 Desired position and actual position vs time |
|
图 5 轨迹跟踪误差曲线 Fig. 5 Trajectory tracking error |
本文研究大型UUV在运动条件下的欠驱动AUV三维轨迹跟踪与回收问题。首先对AUV进行建模,建立了AUV的运动学、动力学模型。其次对回收过程进行分析,根据大型UUV、AUV所搭载的传感器的特点,将回收过程分为了2个阶段。基于上述模型和回收策略,通过反步法设计了三维运动控制器,并进行仿真验证。根据结果可知,所设计的回收策略及控制方法可解决搭载平台运动条件下欠驱动AUV的三维跟踪及回收问题。
| [1] |
MONTANARI M, EDWARDS JR, SCHMIDT H. Autonomous underwater vehicle-based concurrent detection and classification of buried targets using higher order spectral analysis[J]. IEEE Journal of Oceanic Engineering, 2006, 31(1): 188-199. DOI:10.1109/JOE.2006.872216 |
| [2] |
CHEN HX, TANG GY, HUANG YM, et al. Adaptive model-parameter-free nonsingular fixed-time sliding mode control for underwater cleaning vehicle[J]. Ocean Engineering, 262.
|
| [3] |
潘光, 黄明明, 宋保维, 等. AUV回收技术现状及发展趋势[J]. 鱼雷技术, 2008, 16(6): 10-14. |
| [4] |
高剑, 李勇强, 李璐琼, 等. 基于航路点跟踪的AUV回收控制[J]. 火力与指挥控制, 2013, 38(8): 4. DOI:10.3969/j.issn.1002-0640.2013.08.028 |
| [5] |
齐贝贝, 宋敏, 王林林, 等. 基于模型预测控制的移动回收站对接控制算法[J]. 自动化与仪表, 2022, 37(11): 5. |
| [6] |
潘伟, 曾庆军, 姚金艺, 等. 全驱动自主水下机器人回收路径跟踪模糊滑模控制[J]. 船舶与海洋工程, 2022, 38(5): 6. |
| [7] |
YE L, JIANG Y, JIAN C, et al. AUV docking experiments based on vision positioning using two cameras[J]. Ocean Engineering, 2015, 110: 163-173. DOI:10.1016/j.oceaneng.2015.10.015 |
| [8] |
LI Y, WEI C, WU Q, et al. Study of 3 dimension trajectory tracking of underactuated autonomous underwater vehicle[J]. Ocean Engineering, 2015, 105: 270-274. DOI:10.1016/j.oceaneng.2015.06.034 |
 2023, Vol. 45
2023, Vol. 45
