2. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003
2. College of Ship and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang, 212003, China
天然气使用前要经过汽化才能为能源消费端所使用,LNG换热器是这一过程的关键设备。传统的印刷板式换热器(Printed Circuit Heat Exchanger,PCHE)通过化学蚀刻以及扩散焊技术制备,受限于蚀刻工艺,其截面形状多为半圆形。随着增材制造技术的兴起,3D打印形状多样的微通道换热器已可实现,且相对于扩散焊的片片焊接成型,整体成型的3D打印,结构强度更高,有着较大的优势。
换热性能是评估换热器优劣的一个重要指标,最近几年,学者们对换热器的研究主要集中于对流道结构的研究,通过设计不同形式的流道结构提高换热器的综合性能,流道截面形状多为半圆形。
Figley等[1]数值模拟研究了直通道PCHE的热工水力性能,定义并计算热效率和总传热系数以描述PCHE的总传热性能。Kim等[2]研究了不同形式直通道PCHE的热工水力性能,推导出了PCHE的效率随几何参数、材料性能和流动条件的函数表达式。Zhao等[3]和贾丹丹等[4-5]模拟了超临界LNG在3种形式PCHE内的流动换热特性,研究发现翼型翅片对换热性能有较大提升,交错布置通道内翼型翅片时,性能最优。Yoon等[6]数值模拟半圆形Z型PCHE的流动换热特性,提出了f与Nu在层流流动的关联式,发现几何形状对f的影响较大,换热器总体设计对Nu影响较大。
Zhao等[7]数值模拟了直通道PCHE内超临界氮气的流动换热特性,利用实验数据拟合了f与Nu的关联式。张霄[8]研究了直通道PCHE内超临界氮气的流动换热特性,通过实验,拟合了氮气传热的经验关联式。Kim等[9]研究了Z型PCHE中氦的流动换热性能,建立了f与Nu的关联式,并利用关联式得到了最优换热器。
目前大多数学者的研究都是针对化学蚀刻加扩散焊制备的PCHE,对于增材制造技术制造的微通道换热器研究较少。本文基于增材制造技术制造的微通道换热器,采用STAR-CCM+数值模拟软件,对工质在微通道内的流动传热进行仿真,建立三维物理模型,研究截面形状、截面面积、入口质量通量以及压力对其流动换热的影响。
1 超临界甲烷热物性变化规律LNG的临界压力为4.59 MPa、临界温度为–82.6℃。LNG换热器工作压力在其临界压力之上,此时换热器芯体内的LNG可认为处于广义超临界状态,超临界流体的传热特性受热物性的影响显著。由于LNG中甲烷占绝大多数,本文用纯净物甲烷代替LNG,研究的甲烷温度变化范围为121~380 K,压力变化范围为12~20 MPa,在大温差的条件下甲烷的热物性变化剧烈,14 MPa压力下甲烷的几种热物性如图1所示。整个换热过程中,压降相对较小,甲烷的热物性可认为是随着温度的改变而改变,在数值模拟计算中拟合超临界甲烷热物性表达为温度的多项式函数。

|
图 1 14 MPa下甲烷热物性参数变化规律图 Fig. 1 Variation of thermophysical parameters of methane at 14 MPa |
流道内对流换热过程满足质量、动量、能量守恒方程。其控制方程如下:
质量守恒方程
| $ \frac{\partial }{{\partial {x_i}}}(\rho {u_i}) = 0 ,$ | (1) |
动量守恒方程
| $ \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) + \frac{{\partial p}}{{\partial {x_i}}} = \rho {g_i} + \frac{\partial }{{\partial {x_i}}}\Bigg[(\mu + {\mu _t})\frac{{\partial {u_i}}}{{\partial {x_j}}}\Bigg] ,$ | (2) |
能量守恒方程
| $ \frac{\partial }{{\partial {x_i}}}({u_i}(\rho E + p)) = \frac{\partial }{{\partial {x_i}}}({k_{eff}}\frac{{\partial T}}{{\partial {x_i}}} + {\mu _i}{\tau _{ij}}){\text{ + }}{S_h} 。$ | (3) |
湍流模型采用SST k-ω模型,如下式:
| $ \frac{{D\left( {\rho {\text{k}}} \right)}}{{D{\text{t}}}}{\text{ = }}\frac{\partial }{{\partial {{\text{x}}_j}}}\left[ {\left( {\mu + {\sigma _{\text{k}}}{\mu _{\text{t}}}} \right)\frac{{\partial {\text{k}}}}{{\partial {{\text{x}}_j}}}} \right] + {\tau _{{{ij}}}}\frac{{\partial {{\text{u}}_{{i}}}}}{{\partial {{\text{x}}_j}}} - {\beta ^*}\rho \omega {\text{k}} ,$ | (4) |
| $\begin{split} \frac{{D\left( {\rho \omega } \right)}}{{D{\text{t}}}}= & \frac{\partial }{{\partial {{\text{x}}_j}}}\left[ {\left( {\mu + {\sigma _{\omega 1}}{\mu _{\text{t}}}} \right)\frac{{\partial \omega }}{{\partial {{\text{x}}_j}}}} \right] + \frac{\gamma }{{{{\text{v}}_{\text{t}}}}}{\tau _{{{ij}}}}\frac{{\partial {{\text{u}}_{{i}}}}}{{\partial {{\text{x}}_j}}} -\\ &{\beta ^*}\rho {\omega ^2} + 2\left( {1 - {F_1}} \right)\rho {\sigma _{\omega 2}}\frac{1}{\omega }\frac{{\partial {\text{k}}}}{{\partial {{\text{x}}_j}}}\frac{{{\partial _\omega }}}{{\partial {{\text{x}}_j}}} 。\end{split}$ | (5) |
换热器芯体由众多几何结构尺寸相同的微通道规则排列形成,对换热器所有芯体进行建模计算难以实现。图2为半圆形直流道换热器芯体结构示意图,在规则排列条件下,可认为各个通道内LNG流动换热特性相同,为简化计算分析,研究对象选取为长度398 mm,不同水力直径的单根直流道,研究超临界LNG在不同流道形状(半圆型、正方形、圆形、椭圆形)以及不同尺寸微通道内的对流传热特性,不同截面尺寸如表1所示。图3给出了半圆形与正方形截面直通道几何模型,图4为直通道进口尺寸示意图。为了保证计算结果的可对比性,相邻冷热通道与相邻冷通道选用相同壁厚,相邻冷热通道壁面厚度1 mm即上下壁面厚度为0.5 mm,相邻冷通道壁面厚度0.5 mm即左右壁面厚度为0.25 mm。

|
图 2 半圆形直流道换热器示意图 Fig. 2 Schematic diagram of semicircular DC channel heat exchanger |
|
|
表 1 不同截面形状截面尺寸 Tab.1 Section dimensions of different section shapes |

|
图 3 半圆形及正方形直通道整体几何模型 Fig. 3 Overall geometric models of semicircular and square straight-through channels |
超临界甲烷冷通道入口的边界条件设置为质量通量进口,出口的边界条件设置为压力出口,左右壁面绝热。上下壁面施加常热流密度,热流密度通过换热器换热功率及换热面积计算得出。固体材料选用STAR-CCM+材料库中的奥氏体不锈钢。

|
图 4 半圆形及正方形直通道进口尺寸示意图 Fig. 4 Schematic diagram of inlet dimensions of semicircular and square straight-through passage |
流体域与固体域的网格使用STAR-CCM+生成,考量网格无关性以保证仿真结果的准确。表2列出了正方形截面5种不同网格数量划分及出口平均温度。出口平均温度较稳定,考虑计算精度和计算时间,本文采用网格数量为4256154的网格划分进行计算与分析。
|
|
表 2 网格独立性验证 Tab.2 Grid independence verification |
采用STAR-CCM+来进行数值仿真。SIMPLE算法用于耦合速度和压力,QUCIK格式用于求解动量方程,其他离散格式均为二阶精度。控制方程残差下降到10−6且出口温度、速度恒定时,认为计算达到收敛。
2.5 数据处理数据处理选取对流换热系数h、努塞尔数Nu和范宁摩擦系数f等。
对流换热系数为:
| $ h = \frac{q}{T_w - T_b} = \frac{q}{{T_w - \left( {{T_{{\text{out}}}} + {T_{{\text{in}}}}} \right)/2}} 。$ | (6) |
式中:q为来自上下壁面的常热流密度;Tw为壁面平均温度;Tb为超临界甲烷的进出口平均温度。
努塞尔数为:
| $ Nu = \frac{{h{D_h}}}{{{\lambda _f}}} 。$ | (7) |
式中:Dh为水力直径;λf为流体平均导热系数。
范宁摩擦系数
| $ f = \frac{{\Delta {P_f}{D_h}}}{{2L{\rho _b}v_b^2}} 。$ | (8) |
式中:
性能评价指标PEC[10]定义如下:
| $ PEC = (N{u_{{i}}}/N{u_0})/{({f_{{i}}}/{f_0})^{1/3}} 。$ | (9) |
对比分析Zhao[7]实验中的模型考量仿真准确性,实验与模拟温差对比如表3所示,最大相对误差为3.2%,表明本文计算模型有较好的精度。
|
|
表 3 实验与模拟结果的相对误差 Tab.3 Relative errors of experimental and simulation results |
将通道长度为398 mm的直通道沿流动方向每39.8 mm为一个单位分为10个节距,用Np表示。以不同截面积(0.64 mm2、1.0 mm2、1.44 mm2、1.96 mm2)椭圆流道为对象,压力14 MPa,质量通量95 kg/(m2·s),上下壁面热流密度45000 W/m2,研究超临界甲烷在椭圆流道内的局部流动与换热特性。由图5可知:出口温度与出口速度随着截面积的增大而增大,在流道的后半段温度升高超临界甲烷密度降低,流速上升较快;截面积越大,低温核心区域面积越大。

|
图 5 椭圆形流道不同截面积下局部平均温度和平均速度 Fig. 5 Local average temperature and average velocity under different cross-sectional areas of elliptical runner |
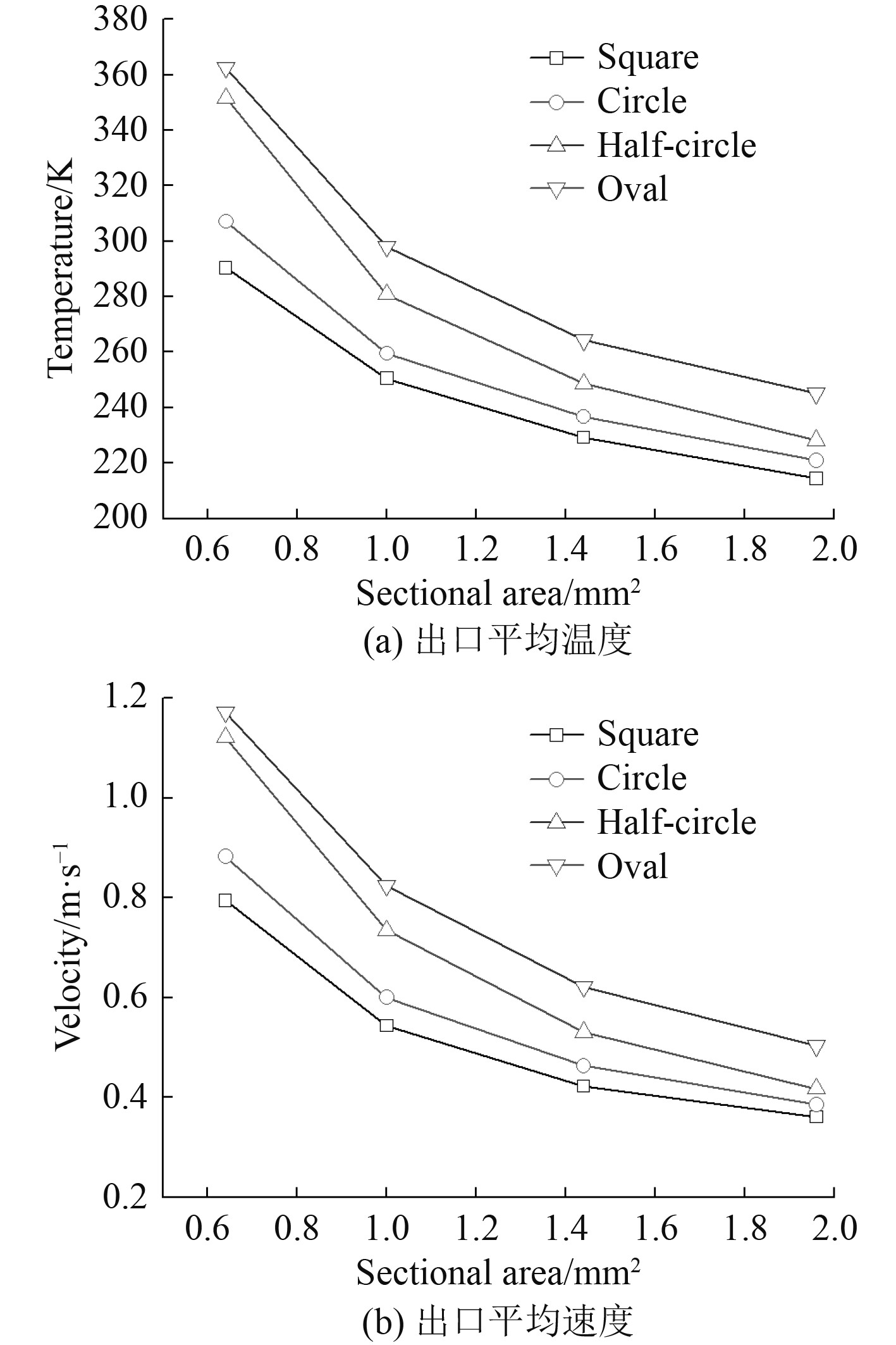
如图6所示,相同的入口质量通量,通道横截面积增大,通道出口温度降低。这是由于随着截面积的增大,单位时间内进入通道的超临界甲烷质量增加,上下壁面的受热面积同时也在增大,但其进口质量增幅更大,从而导致出口温度降低。出口速度与出口温度有着相同的变化趋势,密度随温度的升高而降低,出口温度越高密度越小,相应的出口速度越大。
|
图 6 不同截面形状、不同截面积下出口平均温度和出口平均速度 Fig. 6 Average outlet temperature and average outlet velocity under different cross section shapes and different cross section areas |
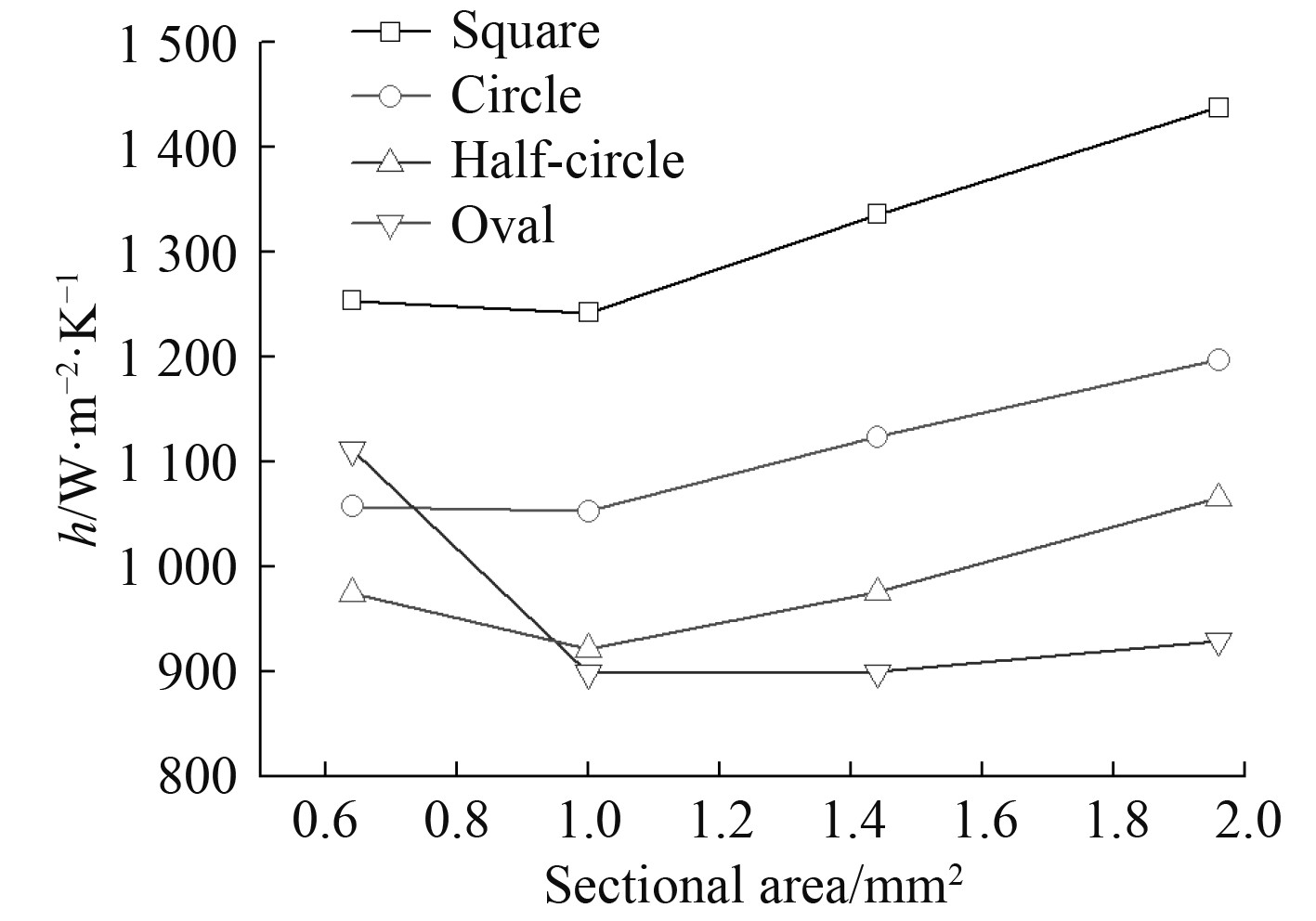
由于受热壁面面积的不同,从出口温度的高低无法评定几种截面形状流道的换热性能。由图7可知,相同截面积下,相较于其他几种通道,正方形通道的总体换热系数更大,在截面积为0.64 mm2时,半圆形通道总体换热系数高于圆形与椭圆形。
|
图 7 不同截面形状、不同截面积下整体换热系数 Fig. 7 Overall heat transfer coefficient under different cross section shapes and cross section areas |
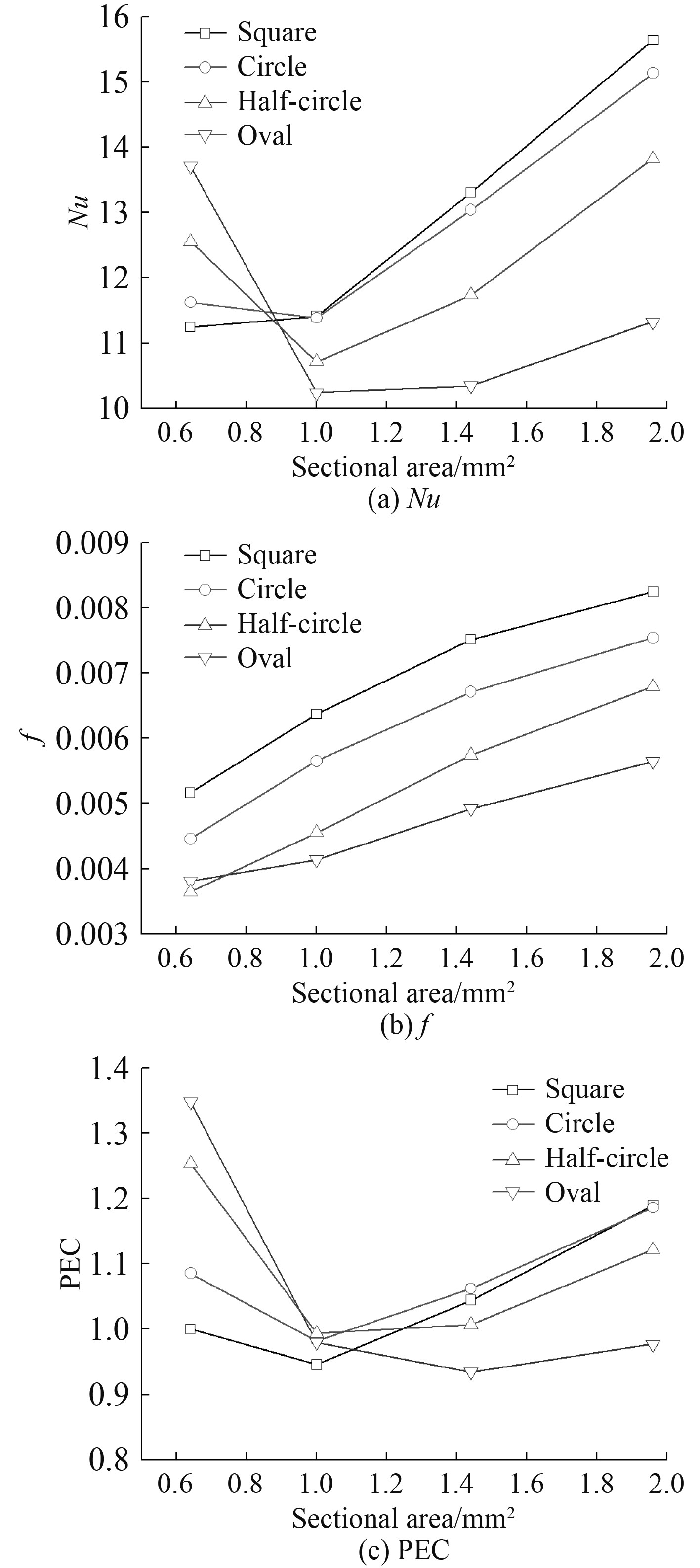
为综合评定不同截面形状的流动与压降性能,采用无量纲数塞尔数(Nu)、范宁摩擦系数(f)、性能评价指标(PEC)进行分析。Nu越大表征流道换热性能越好;f越小表征通道流动性能越好;PEC越大通道综合性能越好。如图8所示,不同截面形状的Nu先减小后增大。在截面积为0.64 mm2时,半圆形通道有着更好的换热性能。随着截面积的增大,正方形通道的换热性能始终优于其他几种通道,其次为圆形、椭圆形、半圆形。f变化的总体趋势是随截面积的增大而增大,对比Nu可以看到,不同截面形状的通道换热性能越好其压降性能就相对较差。采用综合性能评价指标PEC分析其换热压降综合性能,基准通道选择进口截面积为0.64 mm2的正方形通道。随着截面积的增大,PEC整体变化趋势是先减小后增大。在进口截面积为0.64 mm2时,相较于正方形流道其他3种流道有更好的综合性能,尤其是半圆形流道PEC达到1.35。半圆形流道PEC在截面积1 mm2及之后都低于1,表明在较大水力直径的通道内,半圆形流道的综合换热性能较低,其他几种流道较优。
|
图 8 不同截面形状、不同截面积下整体Nu、f及PEC Fig. 8 Overall Nu, f and PEC under different cross section shapes and cross section areas |
在95~235 kg/(m2·s)进口质量通量范围内,研究质量通量对超临界甲烷在截面积为0.64 mm2的椭圆微细流道内的流动与换热影响。如图9所示,壁面平均温度和出入口平均温度随质量通量增大而降低。在质量通量为95 kg/(m2·s),两者的温差为46.2 K,质量通量为235 kg/(m2·s),两者的温差为22.6 K,换热系数与两者温差成反比,在模拟的入口质量通量范围内,质量通量的增大会提高通道的整体换热系数。

|
图 9 不同质量通量下壁面平均温度、出入口平均温度和整体换热系数 Fig. 9 Average wall temperature, average inlet and outlet temperature and overall heat transfer coefficient under different mass fluxes |
在进口质量通量在235 kg/(m2·s),进口温度121 K,选取截面积为0.64 mm2的椭圆流道,研究压力(12、14、16、18、20 MPa)对流动换热影响。如图10所示,出口平均温度和通道整体换热系数随压力的升高而增大,压力从12 MPa变化到20 MPa,出口平均温度增加22.3 K,换热系数增大约10%。这是由于随着压力的升高,在临界温度附近,定压比热容的峰值降低较为明显,温度升高较容易。以12 MPa为基准,计算得到PEC,PEC都小于1,且随入口压力的升高而降低,表明在较低的压力下,通道综合换热性能较优。

|
图 10 不同压力下出口平均温度、整体换热系数和PEC Fig. 10 Average outlet temperature, overall heat transfer coefficient and PEC under different pressures |
以甲烷代替LNG,采用单通道进行模化,在考量了仿真准确性后,采用出口温度、换热系数、PEC等参数对流动换热性能进行评定,得到结论如下:
1)不同截面形状的流道,截面积相同时,正方形流道与其它流道相比换热系数提高约12.8%~28.6%。换热系数与PEC随截面积的增大先减小后增大。在截面积为0.64 mm2时,半圆形及椭圆形流道PEC分别达到1.35和1.25。
2)质量通量从95 kg/(m2·s)增大至235 kg/(m2·s),壁面与流体的平均温差减小23.6 K,换热系数从974.4 W/(m2·K)增大至1991.1 W/(m2·K)。
3)压力从12 MPa升高到20 MPa,出口平均温度增加22.3 K,换热系数增大约10%,但PEC减小约12%,综合性能降低。
| [1] |
JUSTIN FIGLEY, XIAODONG SUN, SAI K. Mylavarapu, et al. Numerical study on thermal hydraulic performance of a printed circuit heat Exchanger[J]. Progress in Nuclear Energy, 2013(68): 89-96. |
| [2] |
WOOJIN KIM, YOUNG-JIN BAIK, SANGWOO JEON, et al. A mathematical correlation for predicting the thermal performance of cross, parallel, and counter flow PCHEs[J]. International Journal of Heat and Mass Transfer, 2017(106): 1294-1302. |
| [3] |
ZHONGCHAO ZHAO, KAI ZHAO, DANDAN JIA, et al. Numerical investigation on the flow and heat transfer characteristics of supercritical liquefied natural gas in an airfoil fin printed circuit heat exchanger[J]. Energies, 2017, 10(11): 18-28. |
| [4] |
贾丹丹. 印刷板式换热器强化换热理论分析与实验研究[D]. 镇江: 江苏科技大学, 2017.
|
| [5] |
贾丹丹, 赵忠超, 张永等. 超临界 LNG 在印刷板式汽化器微细流道内的流动与换热性能数值研究[J]. 船舶工程, 2017(39): 35-40. |
| [6] |
SU-JONG YOON, JAMES O'BRIEN, MINGHUI CHEN, et al. Development and validation of Nusselt number and friction factor correlations for laminar flow in semi-circular zigzag channel of printed circuit heat exchanger[J]. Applied Thermal Engineering, 2017(123): 1327-1344. |
| [7] |
ZHONGCHAO ZHAO, XIAO ZHANG, KAI ZHAO, et al. Numerical investigation on heat transfer and flow characteristics of supercritical nitrogen in a straight channel of printed circuit heat exchanger[J]. Applied Thermal Engineering, 2017(126): 717-729. |
| [8] |
张霄. 印刷板式汽化器汽化性能分析与研究[D]. 镇江: 江苏科技大学, 2017.
|
| [9] |
In Hun Kim, Hee Cheon No. Physical model development and optimal design of PCHE for intermediate heat exchangers in HTGRs[J]. Nuclear Engineering and Design, 2012(243): 243-250. |
| [10] |
WEBB R L, Performance evaluation criteria for use of enhanced heat transfer surfaces in heat exchanger design[J]. Pergamon, 1981(24): 715–726.
|
 2023, Vol. 45
2023, Vol. 45
