现如今,如何提高船舶自动化水平,以保障船舶在海上航行时的可靠性已成为控制理论应用于航海领域的主要研究内容[1-2]。在欠驱动路径跟踪控制问题中,研究主要致力于处理海洋环境干扰和船舶模型不确定性等因素对控制系统的影响[3]。首先,船舶载重量、航行速度和水流速度的变化可引起船舶水动力系数的变化,这种干扰带来体系内部的不确定性。其次,船舶航向过程中风、浪、流会产生干扰力和干扰力矩作用在船体外部,不便估测,为控制器设计带来不便。国内外学者对船舶路径跟踪控制器设计提出了各种方法,王仁强等[4]利用反步法的思想,通过将控制器的设计与Lyapunov函数相结合,并对所引入的虚拟控制输入逐步递推最终得到控制律。该方法针对复杂非线性系统可以较为有效的设计控制器。在航向控制系统中,考虑到执行器输入饱和特性的情况,林郁等[5]采用反演控制算法,加入饱和内补偿辅助系统,设计了船舶航向鲁棒控制器。所设计的控制器在保障性能的前提下,很大程度简化了系统结构。李宗宣等[6]将改进的径向基函数(Radical Basis Function, RBF)神经网络与滑模控制相结合,设计航向控制器,对总不确定项进行逼近,同时有效抑制因滑模面变化过大而产生的抖振。邓华等[7]利用改进的遗传算法对神经网络进行优化,提高了RBF神经网络的逼近性能,并对控制输入进行补偿。沈智鹏等[8]和张晓玲等[9]考虑船舶所受外界环境干扰未知以及系统计算量过大引起的“微分膨胀”问题,提出了一种自适应动态面滑模控制器,利用低通滤波器求解虚拟控制的导数,简化便于控制器的设计。韩俊庆等[10]和秦贝贝等[11]分别利用视线导航法和扩张状态观测器与自抗扰技术结合,用于解决航向控制中的外部和内部扰动问题。实验证明,所设计控制器能很好抵抗外界干扰,并有效减少了控制输出抖振现象,最终实现高精度的航迹跟踪控制。除此之外,模型预测控制[12]、模糊控制[13]等技术也逐渐运用到船舶运动控制中。
参考上述研究成果,结合文献[14],在设计滑模控制器时引入积分滑模面来提高收敛速度,同时采用自适应技术对内外不确定项进行自适应补偿。通过设计改进后非线性观测器,对难以测量的速度进行观测。
1 船舶数学模型大部分数学模型通常缺乏通用性,导致许多仿真实验有时会损害水动力数据对仿真的适应能力。为了避免这种情况,考虑到模型试验的简单性、精确性,以及对水动力特性的适用性,提出一种欠驱动船舶仿真方法的数学模型——MMG分离式模型[15]。
欠驱动船舶在实际运动过程中被认为是有6个自由度的刚体。然而,对于大多数船舶的运动和控制问题,可以忽略起伏、俯仰和横摇运动。因此,将船舶数学模型简化为3个自由度,只考虑船舶的前进、横漂和首摇运动[16]。描述船舶的操纵运动时,通常采用如图1所示的2种不同的坐标系,其中O-X0Y0Z0为惯性坐标系,O为船舶起始点,船舶中心线与X0轴夹角为船舶首向角φ,o-xyz为运动坐标系。其中,船舵与船舶中心线的夹角为舵角,绕oz轴旋转的为转首角速度r,U为船舶运动合速度,其在运动坐标轴上的分量分别为前进速度u和横漂速度vm。漂移角为β=arctan(-vm/u)。

|
图 1 船舶运动平面图 Fig. 1 Ship motion plan |
在海洋环境影响下的MMG数学模型表达式为:
| $ \left\{ \begin{aligned} & \dot x = u\cos \varphi - v\sin \varphi {\text{ = }}\sqrt {{u^2} + {v^2}} \cos (\varphi + \beta ) ,\\& \dot y = u\sin \varphi + vcos\varphi {\text{ = }}\sqrt {{u^2} + {v^2}} \sin (\varphi + \beta ) ,\\& u = \frac{{{m_{22}}}}{{{m_{11}}}}vr - \frac{{{X_u}}}{{{m_{11}}}}u - \frac{{{X_{\left| u \right|u}}}}{{{m_{11}}}}\left| u \right|u + \frac{1}{{{m_{11}}}}{F_u} + {d_{wu}} ,\\& v = \frac{{{m_{11}}}}{{{m_{22}}}}ur - \frac{{{Y_v}}}{{{m_{22}}}}v - \frac{{{Y_{\left| v \right|v}}}}{{{m_{22}}}}\left| v \right|v + {d_{wv}} ,\\& r = \frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}uv - \frac{{{N_r}}}{{{m_{33}}}}r - \frac{{{N_{\left| r \right|r}}}}{{{m_{33}}}}\left| r \right|r + \frac{1}{{{m_{33}}}}{T_r} + {d_{wr}} 。\end{aligned} \right. $ | (1) |
式中:m11、m22、m33为船舶各个方向上的附加质量;Xu、Yv、Nr、Xuu、Yvv、Nrr为水动力阻尼系数;Fu、Tr分别为操纵装置的推进力和转船力矩;dwu、dwv、dwr分别为风、浪、流等外界环境因素作用在船体上的等效干扰。
船舶设计模型使用Norrbin非线性数学模型,考虑到操舵伺服系统会影响控制器的性能,所以在设计模型中考虑舵机伺服系统特性,加入一阶惯性方程,则最终船舶设计模型如下:
| $ \left\{ \begin{aligned} & \dot \varphi {\text{ = }}r ,\\& \ddot \varphi + \frac{1}{T}\dot \varphi + \frac{\alpha }{T}{{\dot \varphi }^3}{\text{ = }}\frac{K}{T}\delta + f ,\\& f = (\vartriangle K{\text{ + }}\vartriangle T{\text{ + }}d) ,\\& \dot \delta = - \frac{{{K_e}}}{{{T_e}}}\delta + \frac{{{K_e}}}{{{T_e}}}{\delta _r} 。\end{aligned} \right. $ | (2) |
式中:T为船舶追随性指数;K为船舶旋回性指数;α为模型非线性系数;f为总干扰项;∆K, ∆T为模型参数摄动;d为外界环境干扰, Ke为舵机控制增益;Te为舵角时间常数;δ为舵角;δr为命令舵角;
| $ \left\{ \begin{aligned} &{{\dot x}_1} = {x_2} ,\\& {{\dot x}_2} = - \frac{\alpha }{T}{x_2}^3 - \frac{1}{T}{x_2} + \frac{K}{T}u + f 。\end{aligned} \right. $ | (3) |
为方便控制系统设计,考虑到船舶的运动特性,对系统做出如下假设:
1)船舶质量均匀,忽略海浪对船体的影响作用。
2)船舶的实时位置(x,y)是可以被获得的,且路径光滑。
3)船舶速度和外界干扰难以测量。对于前进速度u、横漂速度vm、外界海洋环境扰动f存在未知常量
4)船舶加速度远小于船舶位移。
2.1 自适应滑模控制器设计控制器在设计时需要满足以下控制目标:在4个假设的条件下,通过跟踪船舶参考首向角,保持船舶的航向控制,准确跟踪规定路径过程。在此基础上,最大程度抑制控制器抖振,节省控制器输出能量,实现更好的操舵,获得更好的控制性能。最后,选择适当系数使得系统整体稳定,保证误差量渐近收敛。
船舶在路径跟踪时会产生横向偏差ye,其为船舶行驶路径与所设计路径之间的差值:
| $ {y_e} = y - {y_d} 。$ | (4) |
本文选取参考路径为定值常数,
| $ {\dot V_0} = {y_e}\dot y = {y_e}\sqrt {{u^2} + {v^2}} sin(\varphi {\text{ + }}\beta )。$ | (5) |
为了使控制系统稳定,结合文献[17]设计如下船舶参考首向角:
| $ {\varphi _{\text{d}}}{\text{ = - }}{{{k}}_{\text{0}}}\arcsin ({k_1}{y_e}) - \beta 。$ | (6) |
其中:k0、k1 为设计参数,且均为正数。
设计滑模控制器,定义误差变量,并对其进行时间求导得:
| $ \left\{ \begin{gathered} e = {x_1} - {\varphi _d} ,\\ \dot e = {x_2} - {{\dot \varphi }_d} ,\\ \ddot e = {{\dot x}_2} - {{\ddot \varphi }_d} 。\\ \end{gathered} \right. $ | (7) |
积分滑模优势就是能保证系统状态一开始就在滑模面上,缩减了系统收敛时间,同时避免了普通滑模控制因受扰动作用重新平衡后产生的稳态误差。定义如下积分滑模面:
| $ s = {x_2} - \int [ {\ddot \varphi _d} - {b_0}\dot e - {b_1}e]{\rm{d}}t ,$ | (8) |
对其求导得:
| $ \dot s = {\dot x_2} - {\ddot \varphi _d}{\text{ + }}{b_0}\dot e{\text{ + }}{{\text{b}}_1}e = \ddot e + {b_0}\dot e + {b_1}e。$ | (9) |
其中,b0和b1为非零正数。为了解决系统加入积分项带来的抖振,选取指数趋近律来设计控制器则有
| $ {{\rm{sgn}}} (t) = \left\{ \begin{gathered} - 1,t \lt 0 ,\\ 0,t = 0 ,\\ 1,t \gt 0 。\\ \end{gathered} \right. $ | (10) |
将式(3)和式(9)代入得:
| $ \begin{split} & - \frac{\alpha }{T}{x_2}^3 - \frac{1}{T}{x_2} + \frac{K}{T}u + f - {{\ddot \varphi }_d} + {b_0}\dot e + {b_1}e =\\& - \eta {{\rm{sgn}}} (s) - ks。\end{split} $ | (11) |
由式(11)可知,设计律可设计为:
| $ \begin{split} & u = \frac{T}{K}\Bigg(\frac{1}{T}{x_2} + \frac{\alpha }{T}{x_2}^3 - \hat f + {{\ddot \varphi }_d} - {b_0}\dot e - {b_1}e -\\& \eta {{\rm{sgn}}} (s) - ks\Bigg)。\end{split} $ | (12) |
式中,
定义Lyapunov函数
| $ \begin{gathered} {{\dot V}_1} = s \dot s + \frac{1}{\gamma }\tilde f \dot {\hat f } = s(\ddot e + {b_0} \dot e + {b_1}e) + \frac{1}{\gamma } \tilde f \dot{ \hat f} 。\\ \end{gathered} $ | (13) |
将式(12)代入,可得:
| $ \begin{aligned}[b] & {{\dot V}_1} = s( - \eta {{\rm{sgn}}} (s) - ks + f - \hat f) - \frac{1}{\gamma }\tilde f\dot {\hat f } =\\ & - \eta \left| s \right| - k{s^2} - \tilde f\Bigg(\frac{1}{\gamma }\dot{ \hat f} - s\Bigg) 。\end{aligned} $ | (14) |
由式(14)可知,为了使
| $ \dot{ \hat f }= \gamma s 。$ | (15) |
针对船舶在航行过程中速度难以测量的问题,利用非线性观测器对船舶速度进行观测。通过式(1)可知,可通过求出船舶位置导数的估计值进而估测横漂速度vm和前进速度u。
| $ \left\{ \begin{aligned} &\hat u = \hat {\dot x}\cos \varphi + \hat {\dot y}\sin \varphi,\\ & {{\hat v}_m} = - \hat {\dot x}\sin \varphi + \hat {\dot y}\cos \varphi 。\\ \end{aligned} \right. $ | (16) |
以x为例参考文献[14],设计一种改进的非线性观测器。
| $ \left\{ \begin{aligned} &\dot {\hat x} = \hat {\dot x} - {c_0}(\hat x - x),\\ & \dot {\hat {\dot x}} = - {c_1}{\left| {\hat x - x} \right|^q}{{\rm{sgn}}} (\hat x - x) 。\\ \end{aligned} \right. $ | (17) |
其中:c0、c1、q为控制器参数,且c0、c1>0,0<q<1。
2.2 控制器稳定性分析选择式(18)所示的Lyapunov函数:
| $ \begin{gathered} {V_2} = \frac{1}{2}{y_e} + \frac{1}{2}{s^2} + \frac{1}{{2\gamma }}{{\tilde f}^2} + \frac{1}{2}{(\hat {\dot x} - \dot x)^2} + \frac{1}{2}\lambda {(\hat x - x)^2} ,\\ \end{gathered} $ | (18) |
对其求导得:
| $ \begin{split} {{\dot V}_2} =& {y_e}{{\dot y}_e} + s \dot s + \frac{1}{\gamma }{\tilde f} \dot {\tilde f} + ({\hat {\dot x}} - \dot x)(\dot {\hat {\dot x}} - \ddot x) + \\ &\lambda (\hat x - x)(\dot {\hat x} - \dot x) 。\end{split} $ | (19) |
将式(6)、式(12)和式(15)代入化简得:
| $ \begin{split} & {{\dot V}_2} = - {y_e}\sqrt {{u^2} + {v_m}^2} \sin ({a_0}\arcsin ({a_1}{y_e})) - \\&ks - \eta s{{\rm{sgn}}} (s) - \lambda {c_0}{(\hat x - x)^2}- \\& (\hat {\dot x }- {\dot x})({c_1}{\left| {\hat x - x} \right|^q}{{\rm{sgn}}} (\hat x - x) -\\& \lambda (\hat x - x)) - \ddot x(\hat {\dot x} - \dot x) 。\end{split} $ | (20) |
因为反三角函数的单调性和符号函数的严格有界性,可推出
对于欠驱动船舶设计模型,本文提出的控制算法式(12)和自适应律式(15)可保证控制系统中所有状态变量在假设建立的前提下全局一致并最终有界,证明完毕。
3 仿真实验 3.1 仿真实验对象以“育龙”船作为仿真实验对象,相关模型参数为:T=216,K=0.478,α=30,Ke=1,Te=2.5 s;船舶初始状态:vm=7.2 m/s, u=0, r=0, φ=0, (x0,y0)=(0,0);外部环境干扰:风速Vwind=10 m/s, 流速Vflow=1.5 m/s,风向和流向如图2所示。

|
图 2 风向、流向示意图 Fig. 2 Wind and flow direction diagram |
图3为船舶运动控制系统设计流程图,其中各类控制器参数为:k0=0.002,k1=π/3,k=0.006,η=0.0015,γ=0.0001,b0=0.008,b1=0.001,c0=0.5,c1=0.001,q=0.5。
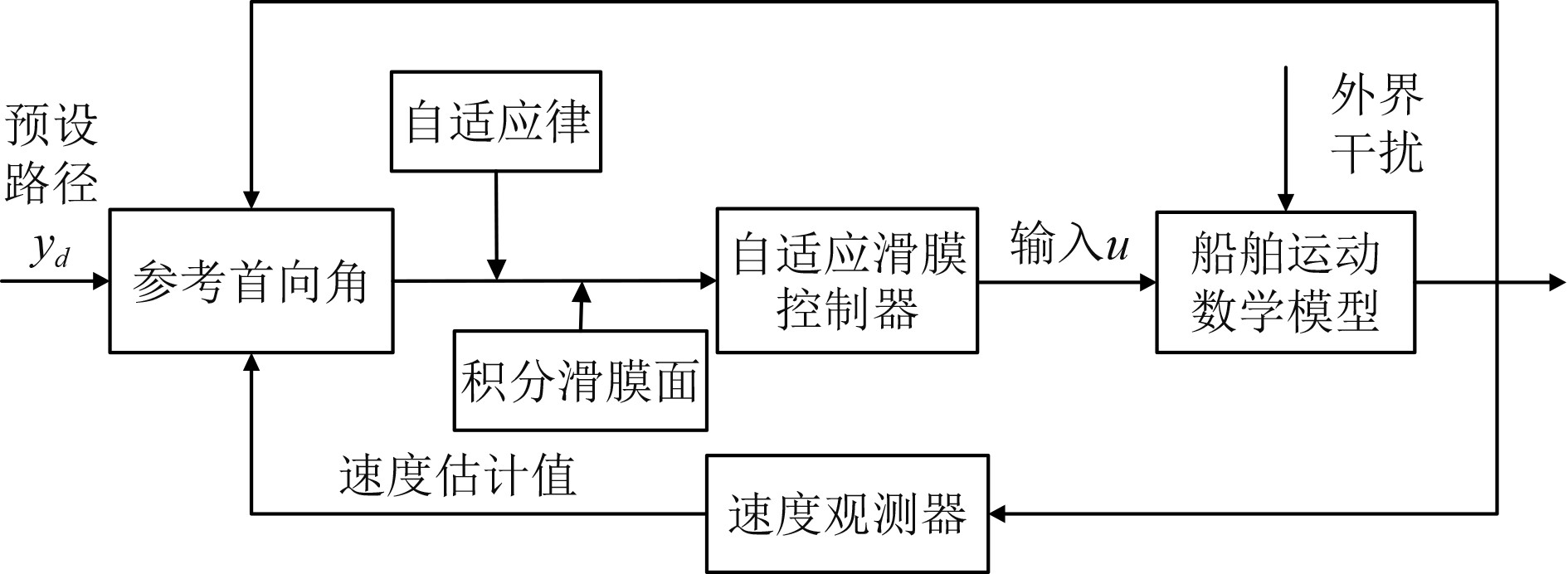
|
图 3 控制器设计流程图 Fig. 3 Controller design flow diagram |
应用 Matlab/Simulink 平台进行船舶运动控制仿真,与普通滑模控制策略进行比较。对比结果如图4~图8所示。
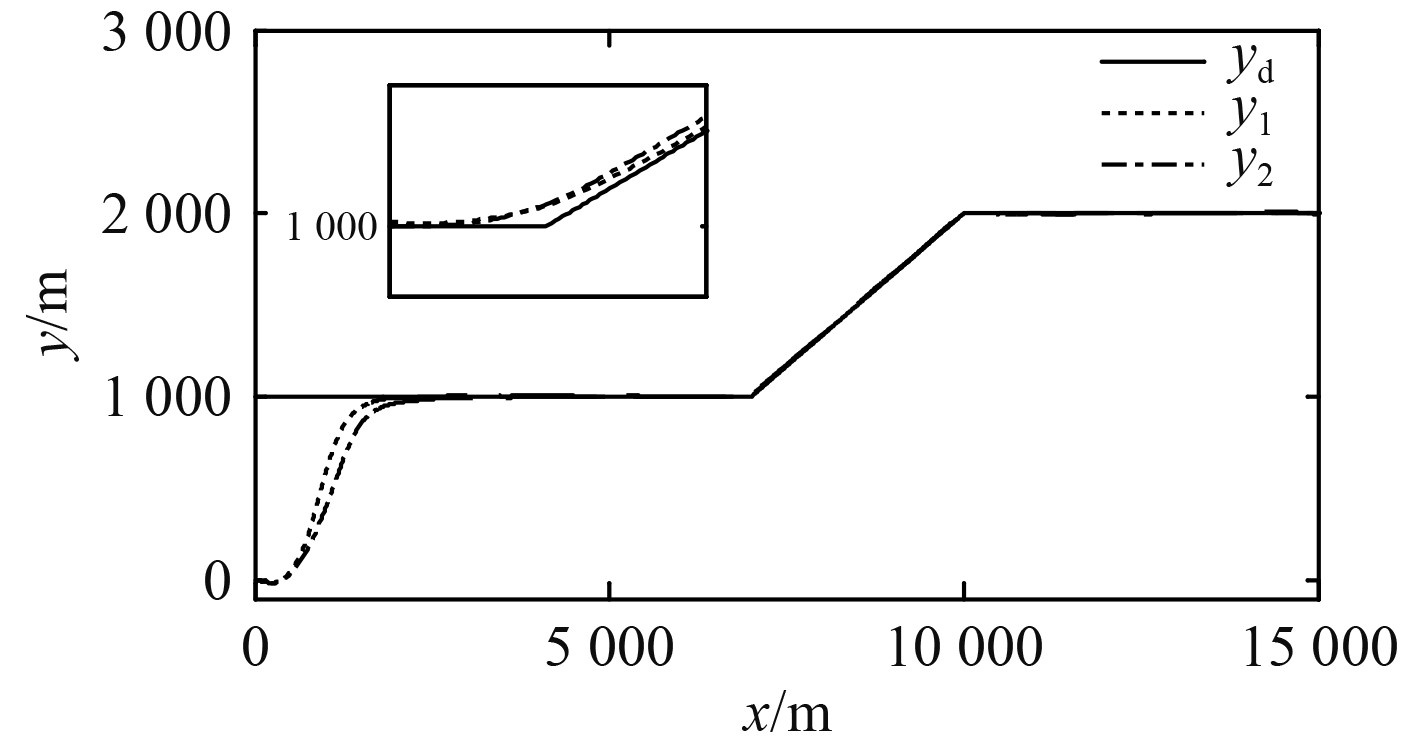
|
图 4 路径跟踪误差图 Fig. 4 Path following error diagram |
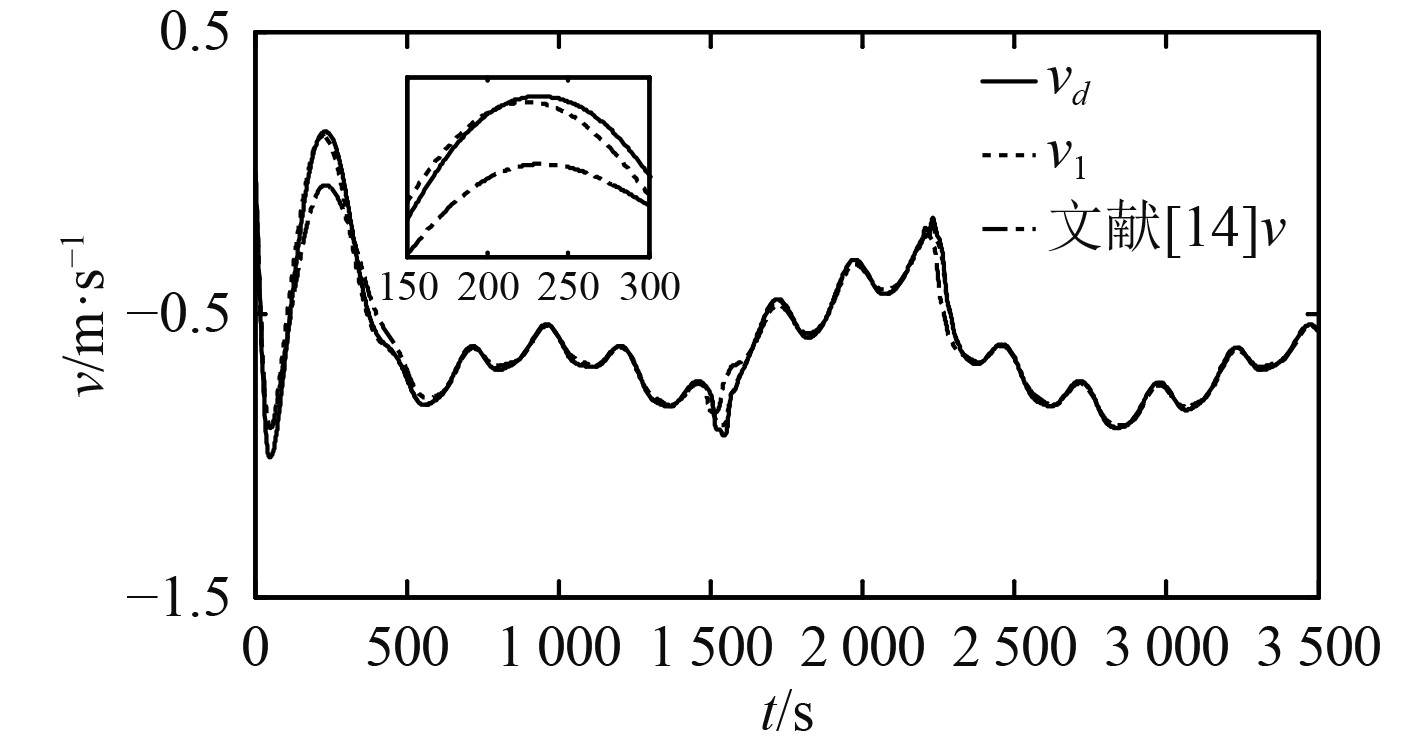
|
图 8 横漂速度观测值 Fig. 8 Drifting velocity observed value |
由图4和图5可知,在2种控制器均能够跟踪预设路径的情况下,基于积分面的自适应滑模控制器较普通滑模控制器跟踪效果更好,且到达稳定所需的时间更少。由图6可知,为使船舶能够准确跟踪既定航线,需不断进行操舵行为。通过公式

|
图 5 路径偏差图 Fig. 5 Path deviation diagram |
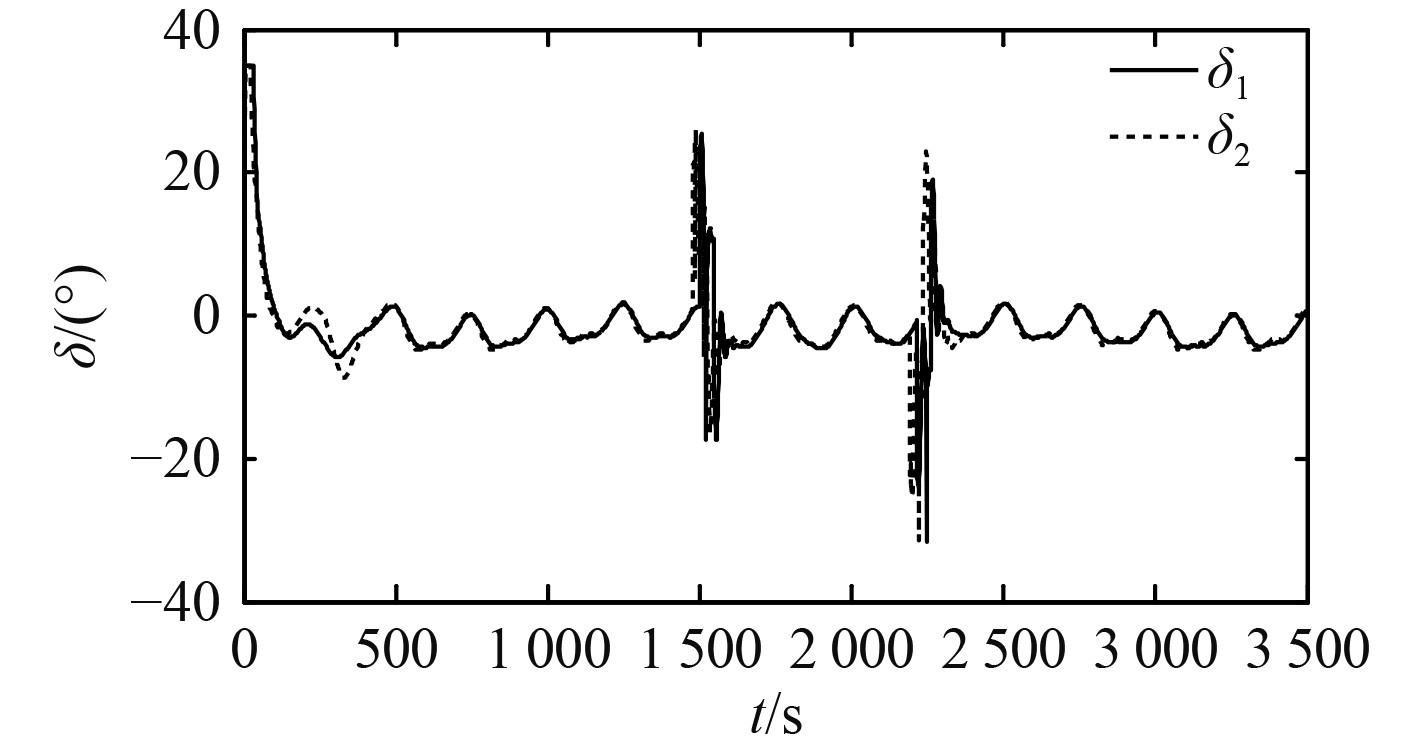
|
图 6 舵角变化图 Fig. 6 Rudder Angle change diagram |

|
图 7 前进速度观测值 Fig. 7 Forward velocity observed value |
针对欠驱动船舶数学模型不确定性和外界环境干扰对船舶运动控制的影响,结合改进的速度观测器,设计带积分面的自适应滑模控制器,并进行仿真实验。结果表明,在给定期望参考航向角前提下,所设计的控制策略能良好的跟踪参考航向角,使船舶跟踪误差迅速收敛,渐进跟踪到期望路径的范围内。舵机响应曲线平滑,同时速度观测器能够对航行速度进行精确的观测,证明所设计控制算法的有效性,符合实际工程的需要。
| [1] |
田佰军, 刘正江, 郑云峰. 考虑暂态/稳态性能的船舶航向保持控制[J]. 哈尔滨工程大学学报, 2016, 37(5): 640-645. TIAN Bai-jun, LIU Zheng-jiang, ZHENG Yun-feng. Robust course-keeping control for ships with the prescribed transient/steady performance[J]. Journal of Harbin Engineering University, 2016, 37(5): 640-645. DOI:10.11990/jheu.201507026 |
| [2] |
FOSSEN T I, PETTERSEN K Y, GALEAZZI R. Line-of Sight path following for dubins paths with adaptive sideslip compensation of drift forces[J]. IEEE Transactions on Control Systems Technology, 2015, 23(2): 820-827. DOI:10.1109/TCST.2014.2338354 |
| [3] |
DO K D, PAN J. Robust path-following of underactuated ships: theory and experiments on a model ship[J]. Ocean Engineering, 2006, 33(10): 1354-1372. DOI:10.1016/j.oceaneng.2005.07.011 |
| [4] |
王仁强, 陈进涛. 船舶航向非线性反演自适应滑模控制[J]. 舰船科学技术, 2014, 36(3): 136-138+142. WANG Ren-qiang, CHEN Jin-tao. Ship heading nonlinear inversion adaptive sliding mode control[J]. Ship Science and Technology, 2014, 36(3): 136-138+142. DOI:10.3404/j.issn.1672-7649.2014.03.028 |
| [5] |
林郁, 苗保彬. 基于Backstepping和输入饱和的船舶航向跟踪控制[J]. 大连海事大学学报, 2014(3): 28-32. DOI:10.3969/j.issn.1006-7736.2014.03.006 |
| [6] |
李宗宣, 卜仁祥, 章沪淦. 结合改进RBF与虚拟圆弧的船舶路径滑模控制[J]. 西北工业大学学报, 2021, 39(1): 216-223.
|
| [7] |
邓华, 王仁强, 胡甚平, 等. 分布式遗传的船舶航向神经网络优化控制[J]. 上海海事大学学报, 2020, 41(4): 15-19+49. DOI:10.13340/j.jsmu.2020.04.003 |
| [8] |
沈智鹏, 毕艳楠, 郭坦坦, 等. 带非线性观测器的欠驱动船舶自适应动态面输出反馈轨迹跟踪控制[J]. 系统工程与电子技术, 2019, 41(2): 409-416. DOI:10.3969/j.issn.1001-506X.2019.02.24 |
| [9] |
张晓玲, 沈智鹏, 毕艳楠. 带扰动观测器的船舶轨迹跟踪自适应动态面滑模控制[J]. 船舶工程, 2018, 40(7): 81-87. DOI:10.13788/j.cnki.cbgc.2018.07.081 |
| [10] |
韩俊庆, 李伟, 孟凡彬, 等. 基于Super-twisting的欠驱动船舶滑模自抗扰控制[J]. 舰船科学技术, 2022, 44(8): 73-78. HAN Jun-qing, LI WEI, MENG Fan-bin, et al. Sliding mode active disturbance rejection control for underactuated ship based on Super-twisting[J]. Ship Science and Technology, 2022, 44(8): 73-78. DOI:10.3404/j.issn.1672-7649.2022.08.015 |
| [11] |
秦贝贝, 陈增强, 孙明玮, 等. 基于自适应神经模糊推理系统的船舶航向自抗扰控制[J]. 智能系统学报, 2020, 15(2): 255-263. DOI:10.11992/tis.201809047 |
| [12] |
王锐利, 林大志. 解析模型预测控制在欠驱动船舶路径跟踪控制中的研究[J]. 舰船科学技术, 2016, 38(6): 73-75. WANG Yan-li, LIN Da-zhi. Research on analytic model predictive control for path tracking control of underactuated Ship [J]. Ship Science and Technology, 2016, 38(6): 73-75. |
| [13] |
QIU De-hui, WANG Qing-lin, YANG JIE. Adaptive fuzzy control for path tracking of underactuated ships based on dynamic equilibrium state theory[J]. International Journal of Computational Intelligence Systems, 2011, 4 (6): 1148-1157.
|
| [14] |
SUN Hao-nan, CHEN Shi-cai, WU Wei-bing. Approach law sliding mode control for path following of underactuated ships with state observer[C]//China Automation Congress. 2021: 4408-4413.
|
| [15] |
YASUKAWA H, YOSHIMURA Y. Introduction of MMG standard method for ship maneuvering predictions[C]//Journal of Marine Science and Technology, 2015, 20(1): 37-52.
|
| [16] |
贾欣乐, 杨盐生. 船舶运动数学模型——机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999: 234–250.
|
| [17] |
章沪淦, 卜仁祥, 李宗宣. 带状态观测器的船舶路径跟踪预测滑模控制[J]. 计算机仿真, 2021, 38(9): 262-266+271. ZHANG Hu-gan, BU REN-xiang, LI Zong-xuan. Predictive sliding mode control for ship path track-ing with state observer [J]. Computer Simulation, 2021, 38(9): 262-266+271. |
 2023, Vol. 45
2023, Vol. 45
