冲击载荷在船舶航行的过程中,会使船舶板架结构产生损伤和裂纹,海洋环境腐蚀又将加速裂纹的扩展,在冲击载荷与海洋环境腐蚀的共同作用下,船舶板架结构的力学性能将加速下降,导致结构寿命缩短,威胁船舶板架安全[1-3]。
本文结合船舶材料体系和服役环境特点,选取某特殊钢集团专门为船舶生产的38CrMoAl圆钢(Φ32 mm)作为研究对象,采用分离式霍普金森压杆设备对38CrMoAl钢试验件进行冲击载荷加载[4-6]。
以38CrMoAl钢材料作为测试试验件,从应力、应变、应变率与应力波几个方面对变载荷作用下的船舶板架结构冲击展开模拟研究,其基于变载荷作用的各项应力关系下式:
| $ \sigma (t) = \frac{{{A_1}}}{{2{A_0}}}E({\varepsilon _{\text{i}}} + {\varepsilon _{\text{r}}} + {\varepsilon _{\text{t}}}) = \frac{{{A_1}}}{{{A_0}}}E{\varepsilon _{\text{t}}} \text{,} $ |
| $ \varepsilon (t) = \frac{c}{{{l_0}}}\int_0^t {({\varepsilon _{\text{i}}} - {\varepsilon _{\text{r}}} - {\varepsilon _{\text{t}}}){\text{d}}t} = - \frac{{2c}}{{{l_0}}}\int_0^t {{\varepsilon _{\text{r}}}} {\text{d}}t \text{,} $ |
| $ \dot \varepsilon (t) = \frac{c}{{{l_0}}}({\varepsilon _{\text{i}}} - {\varepsilon _{\text{r}}} - {\varepsilon _{\text{t}}}) = - \frac{{2c}}{{{l_0}}}{\varepsilon _{\text{r}}} \text{。} $ |
为了验证试验获得的38CrMoAl钢材料J-C本构模型和断裂参数的有效性,在ABAQUS有限元仿真软件中建立38CrMoAl钢动态试验模型,并采用显式动力学算法对试验获取的J-C本构模型和断裂参数进行验证。
1 显式动力学算法ABAQUS有限元软件中的显式非线性动态求解方法,可以应用在变载荷作用下的相关数据求解。在具体研究思路上,可以采用差分处理的方式对运动方程进行时间积分。通过应用前一个时步的运动条件直接求解下一个时步的运动条件,相对于隐式算法,该算法不需要进行迭代计算,计算速度快,计算所需资源少,稳定性好,也不存在收敛问题。因此被广泛应用于动态力学的仿真计算中,获得了很好的效果。显式动力学有限元算法的计算过程如下:
假设开始时为t时刻,程序求解动力学平衡方程式为
| $ M\ddot u = P - I \text{,} $ |
基于以上数据计算加速度为
| $ {\ddot u_{(t)}} = {(M)^{ - 1}}{(P - I)_{(t)}} \text{。} $ |
式中:M为质量;
| $ {\dot u_{(t + \frac{{\Delta t}}{2})}} = {\dot u_{(t - \frac{{\Delta t}}{2})}} + \frac{{\Delta {t_{(t + \Delta t)}} + \Delta {t_{(t)}}}}{2}{\ddot u_{(t)}} 。$ |
对速度进行积分,可得到时步结束时的位移为
| $ {u_{(t + \Delta t)}} = {u_{(t)}} + \Delta {t_{(t + \Delta t)}}{\dot u_{(t + \frac{{\Delta t}}{2})}} 。$ |
根据应变速率ε,计算单元的应变增量dɛ,再由本构关系计算应力σ:
| $ {\sigma _{(t + \Delta t)}} = f({\sigma _{(t)}},{\rm{d}}\varepsilon ) \text{。} $ |
在ABAQUS有限元分析软件中建立准静态拉伸试验、SHPB试验和SHTP试验模型,模型尺寸与试验保持一致。准静态拉伸试验件有限元模型如图1所示,该结构件采用C3D8R结构网格,并对试验件的中部网格进行加密,共建立网格4816个。

|
图 1 准静态拉伸试验件有限元模型 Fig. 1 Finite element model of quasi-static tensile test piece |
SHPB模型如图2所示,模拟变载荷冲击长度为300 mm,入射杆和透射杆长度为1 250 mm,直径均为15 mm。模拟变载荷冲击和杆系材料均为18Ni钢,材料密度为7800 kg/m3,弹性模量为210 GPa,泊松比为0.3。采用C3D8R六面体网格,并对中心杆附近的网格进行加密,共设置网格数196200个。

|
图 2 SHPB试验有限元模型 Fig. 2 SHPB test finite element model |
SHTP模型如图3所示,该模型的网格密度较为稀疏,但是仿真速度可以获得成倍的提升,有利于提升仿真效率。

|
图 3 SHTP试验有限元模型 Fig. 3 SHTP test finite element model |
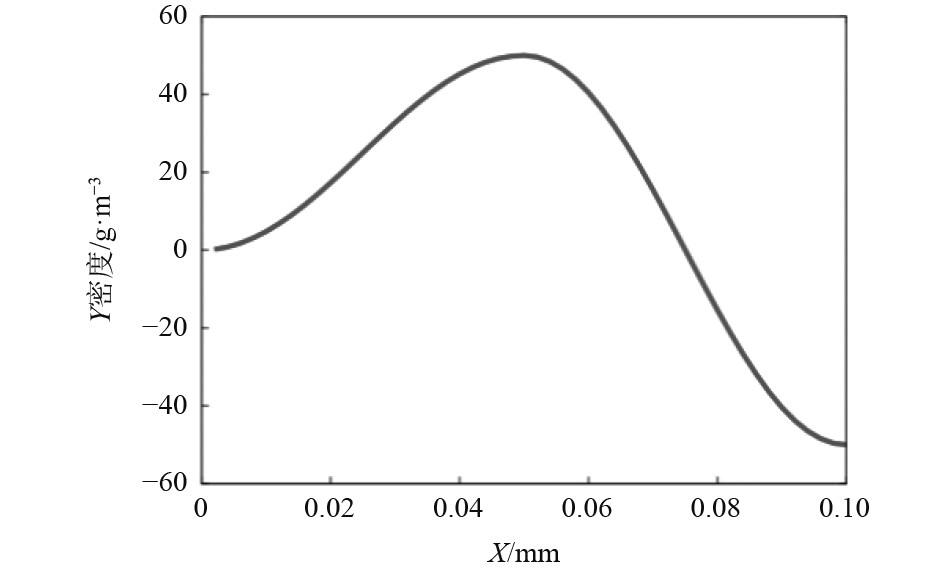
有限元模型Y密度分布图如图4所示。采用C3D8R六面体结构网格,并对试验件和杆系靠近试验件一端网格进行加密,共建立网格数231100个。
|
图 4 SHTP试验件有限元模型Y密度分布图 Fig. 4 Y density distribution diagram of SHTP specimen finite element model |
对本文建立的变载荷作用下船舶板架结构模拟显式动力学有限元模型进行仿真计算,并对应力波传播过程进行分析。建立38CrMoAl钢动态三维有限元模型,采用试验-数值法和振动分析法对不同周期盐雾腐蚀后的38CrMoAl钢材料进行高应变速率加载下的动态断裂韧性测试。
利用改进后的霍普金森压杆装置获得38CrMoAl钢材料在高应变速率下的应力波传播模型,通过结合建立的动态断裂韧性有限元模型,仿真得到了动态应力强度因子的时程曲线,并确定了不同盐雾腐蚀周期后38CrMoAl钢的动态断裂韧性。其材料单元的损伤演化公式如下:
| $ {D_0} = \sum (\Delta \varepsilon _{eq}/\varepsilon _f) \text{。} $ |
基于以上研究,得出SHPB试验中应力波在压杆和试验件中的传播过程和应力状态,并归纳得出当t=0 µs时,会产生入射波;当t=250 µs时,试验件开始受力变形;当t=370 µs时,试验件压缩变形达到最大,随后进入应力卸载阶段;t=500 µs时,应力波到达透射杆末端。围绕试验件的断裂应变,得到了试验件拉伸的断面面积为:
| $ {\varepsilon _f} = \ln ({A_2}/{A_{{f}}}) \text{,} $ |
准静态条件的静水应力为:
| $ {\sigma ^*} = \frac{1}{3} + \ln \left( {1 + \frac{{{d_0}}}{{4R}}} \right) \text{。} $ |
由此得到了SHPB试验中应力波在压杆和试验件中的传播过程和应力状态,船舶板架在变载荷的影响下,其应力波传播也会变得更复杂一些。
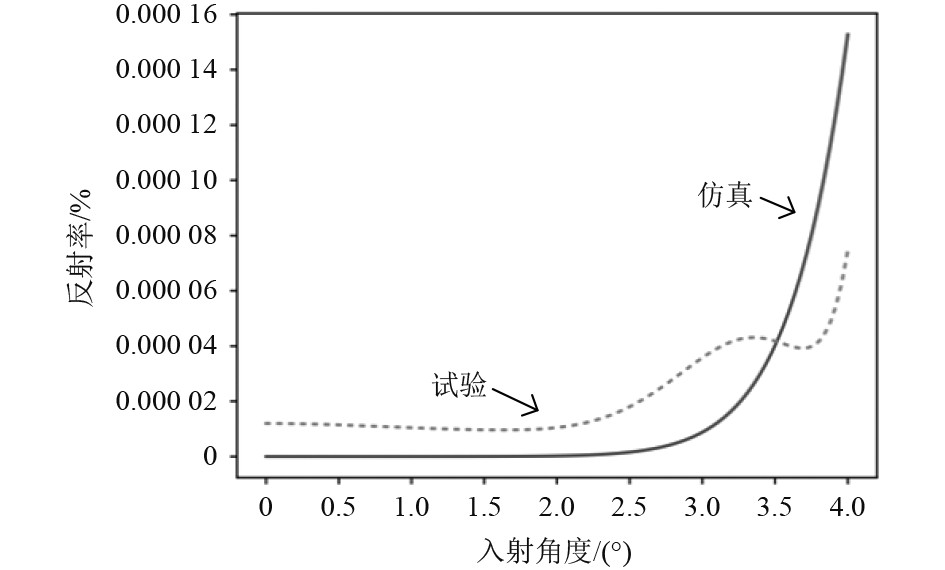
此外在关于SHPB试验中,按照时间顺序,38CrMoAl钢材料在进行模拟船舶板架结构中,其试验件在结构冲击下开始被拉伸、变形达到最大,并在最终的卸载阶段应力波到达透射杆末端。为了保持数值模拟与试验的一致性,取入射杆和透射杆中点的两单元作为输出,入射波反射率分布曲线如图5所示。
|
图 5 入射波反射率分布曲线 Fig. 5 Incident wave reflectivity distribution curve |
采用二波法对产生的入射、透射波形进行处理,得到试验件材料的应变曲线。试验件数值模拟与J-C本构模型对比如图6所示。

|
图 6 试验件数值模拟与J-C本构模型对比 Fig. 6 Comparison between numerical simulation of test piece and J-C constitutive model |
通过图6可见,数值模拟结果与J-C本构方程一致,表明数值模拟结果准确可信。
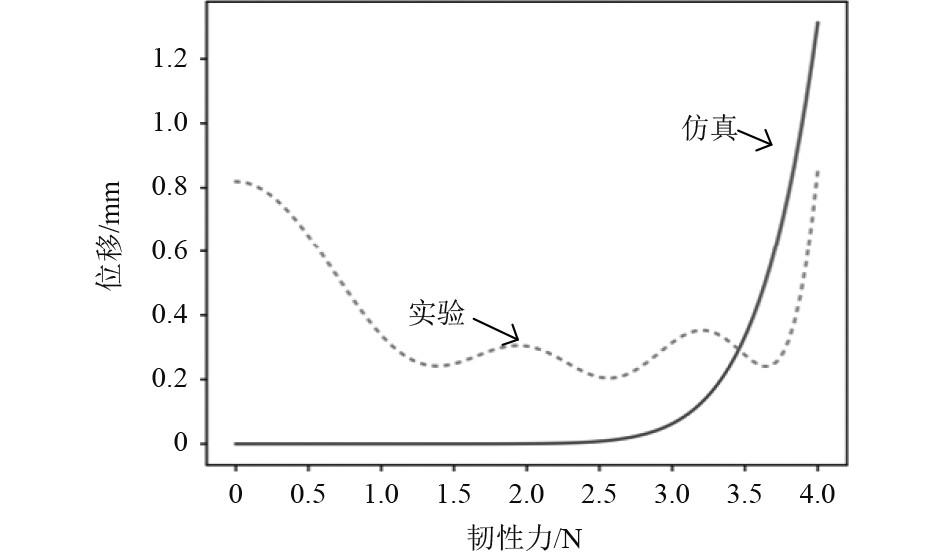
4 断裂韧性计算结果与评估分析 4.1 准静态断裂韧性计算结果在MTS810疲劳试验机上对未腐蚀和盐雾腐蚀10 d、20 d、30 d的38CrMoAl钢试验件进行准静态断裂韧性测试,得出试验获得的力-位移,准静态断裂韧性力-位移曲线如图7所示。
|
图 7 准静态断裂韧性力-位移曲线 Fig. 7 Quasi static fracture toughness force displacement curve |
由此可见,38CrMoAl钢在准静态加载下的断裂韧性随着加载速率的增加略有增加,但增幅不大,位移曲线的仿真试验值在2.5 N作用力时差距最小。
此外,38CrMoAl钢在准静态加载下的断裂韧性随着盐雾腐蚀时间的增加而减小,盐雾腐蚀30 d时,38CrMoAl钢材料断裂韧性下降至53.73 MPa·m1/2,断裂韧性下降了4.7%。
4.2 动态断裂韧性评估分析将38CrMoAl钢代入到断裂韧性有限元模型中进行计算,获得试验件在动态冲击加载下的应力传播过程。
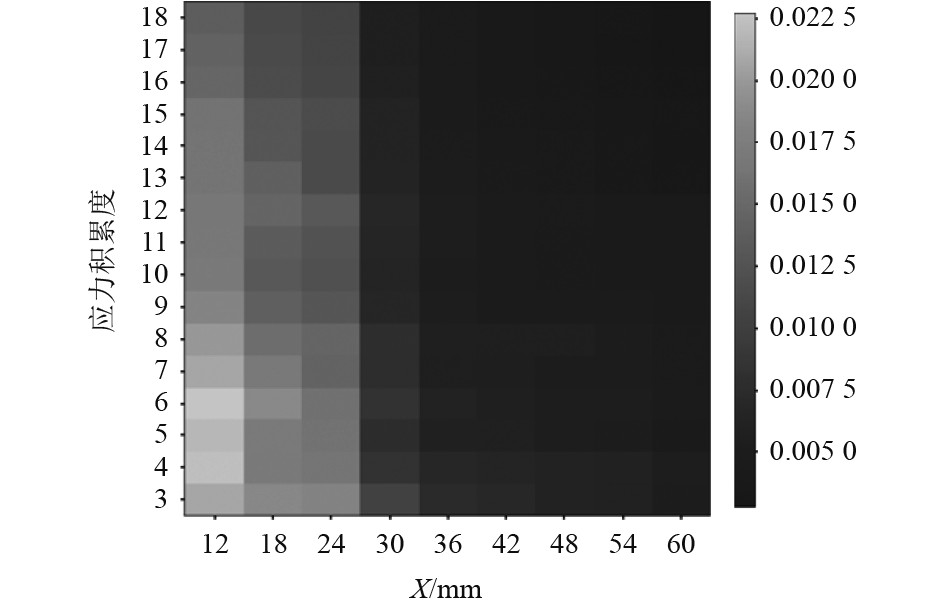
为了分析试验件在动态受力中的内部应力变化过程,对应力的积累程度进行模拟仿真实验,从而可以获得截取试验件的剖面图,并由此展示了应力波从试验件开始被加载至加载完成进入卸载阶段的全过程。为了验证数值模拟的准确性,对试验中试验件裂纹尖端附近应变片获得的应变信号与数值模拟获得的应变值进行对比,如图8所示。
|
图 8 38CrMoAl钢试验件裂纹尖端附近应变片所测应变与数值模拟结果对比 Fig. 8 Comparison between the strain measured by strain gauge near the crack tip of 38CrMoAl steel specimen and the numerical simulation results |
本文数值模拟结果与试验值基本一致,表明数值模拟方法可以准确模拟38CrMoAl钢的动态起裂过程。当加载时间到达起裂点时,试验件起裂导致应力监测信号剧烈减小,从而获得了船舶板架结构冲击评估方法。目前对承受冲击载荷与海洋环境共同作用的船舶板架结构件的研究还需要解决3个问题:一是结构在服役中承受的加载应变率及载荷实测数据的获取;二是在高速冲击下,结构的应变率与损伤程度的量化;三是对结构在冲击载荷与海洋环境共同作用下的服役寿命进行有效的评估。
| [1] |
李怿, 李典, 侯海量, 等. 螺栓连接结构对舰船复合材料夹芯板架冲击动响应的影响[J]. 兵器装备工程学报, 2022, 43(9): 343-350. LI Yi, LI Dian, HOU Hai-liang, et al. Influence of Bolted Connection Structure on Shock Dynamic Response of Ship Composite Sandwich Panel Frame[J]. Chinese Journal of Ordnance Equipment Engineering, 2022, 43(9): 343-350. |
| [2] |
郭德松, 纵帅, 王秀飞, 等. 集装箱坠落载荷作用下甲板板架结构响应理论预报方法研究[J]. 振动与冲击, 2021, 40(21): 142-149+193. GUO De-song, ZONG Shuai, WANG Xiu-fei, et al. Research on Theoretical Prediction Method of Deck Grid Structure Response under Container Falling Load[J]. Vibration and Shock, 2021, 40(21): 142-149+193. |
| [3] |
王鹏飞. 含腐蚀损伤板架结构极限强度评估及工程应用[D]. 大连理工大学, 2020 WANG Peng-fei. Ultimate Strength Evaluation and Engineering Application ofStiffened Panel with Corrosion Damage [D]. Dalian University of Technology, 2020. |
| [4] |
杨正伟, 赵志彬, 李胤, 等. 压-压疲劳载荷下CFRP层合板表面红外辐射特征[J]. 航空学报, 2021, 42(5): 231-241. YANG Zheng-wei, ZHAO Zhi-bin, LI Yin, et al. Characteristics of infrared radiation on the surface of CFRP laminates under compression-compression fatigue loads[J]. Acta Aeronautica Sinica, 2021, 42(5): 231-241. |
| [5] |
王逸南, 姚熊亮, 王治, 等. 基于物质点法的船体板架结构高速侵彻毁伤模式研究[J]. 爆炸与冲击, 2021, 41(10): 90-102. WANG Yi-nan, YAO Xiong-liang, WANG Zhi, et al. Research on high-speed penetration damage model of hull grillage structure based on material point method[J]. Explosion and Shock, 2021, 41(10): 90-102. |
| [6] |
赵松涛, 王南, 王鑫, 等. 水下爆炸作用下船舶结构与燃气轮机动态响应的数值研究[J]. 船舶力学, 2021, 25(6): 815-827. ZHAO Song-tao, WANG Nan, WANG Xin, et al. Numerical study on dynamic response of ship structure and gas turbine under underwater explosion[J]. Ship Mechanics, 2021, 25(6): 815-827. |
 2023, Vol. 45
2023, Vol. 45
