目前关于波浪载荷的试验研究,多是采用模型试验的方式,对兴波阻力在失效时进行直观的观察与分析,并对船体本身结构作用进行研究。有学者以中小型高速船为例,深入探讨了水上不同环境作用下,其对船舶接触面的压力大小[1-3]。也有研究基于单双铰弯曲的失效模式,分别对不同航速的高速船进行分析,得出了能够适应不同船舶载荷的最佳模型参数。此外,在斜面结构试验的基础上,也有学者结合相关的数据结果,深入探究在波浪斜面结构时,其局部压力的大小与分布,以及结构间的相互作用。
在关于不同兴波阻力的高速船移动载荷研究中,有学者在三维圆盘单元模型的基础上,分析了不同水面与船舶结构间的相互作用。此外,在利用有限元的载波研究过程中,需要充分考虑到三角和正弦载荷的兴波阻力作用。虽然学者们基于不同的模型对水上高速船的兴波阻力以及波浪载荷进行了相关研究,但是在关于高速船波浪载荷方面,尚没有Rankine源方法作为理论研究支撑[4-7]。
为了探讨该计算方法的可行性,本文以高速船中的小型半潜式快艇为例,对其展开应用分析,探讨具有一定可靠安全性、高效性的算法,为高速船的研究带来参考价值。
1 半潜式快艇主要设计参数 1.1 主要尺寸参数选定本文所选择的半潜式快艇,整体设计参数见表1。
|
|
表 1 半潜式快艇参数表 Tab.1 Parameters of semisubmersible speed craft |
拟定其装载总量为500 kg,配备1名驾驶员(人员重量按65 kg/人计算)。
1.3 主要性能参数选定半潜式快艇设计动力参数的参考对象是同等级别的汽车动力参数,其主要参数有加速时间、比转矩、比功率、I档最大动力因素
|
|
表 2 半潜式快艇动力参数汇总表 Tab.2 Summary of power parameters for semisubmersible speed craft |
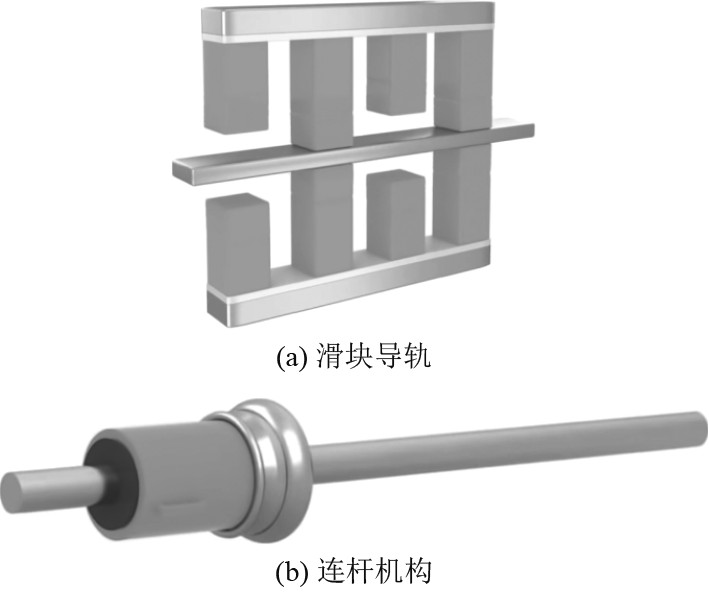
如图1所示,对油气弹簧减震器和普通螺旋弹簧减震器进行设计,将其位置选定在前后悬架中,从而让悬架系统的可靠性更高,同时也能够直接提高这2种减震器的定位精度。
|
图 1 减振系统定位点示意图 Fig. 1 Vibration reduction system positioning point diagram |
油气弹簧上支点定位的准确性又受到滑块定位的直接影响,为了确保滑块稳定可靠的工作,在设计滑块导轨时需要限制螺丝纹杠沿着轴线方向运动,并在滑块安装限位开关来实现对反馈控制效果的作用,以此来避免因滑块超出安全位置而影响整个悬架系统正常运转的情况。
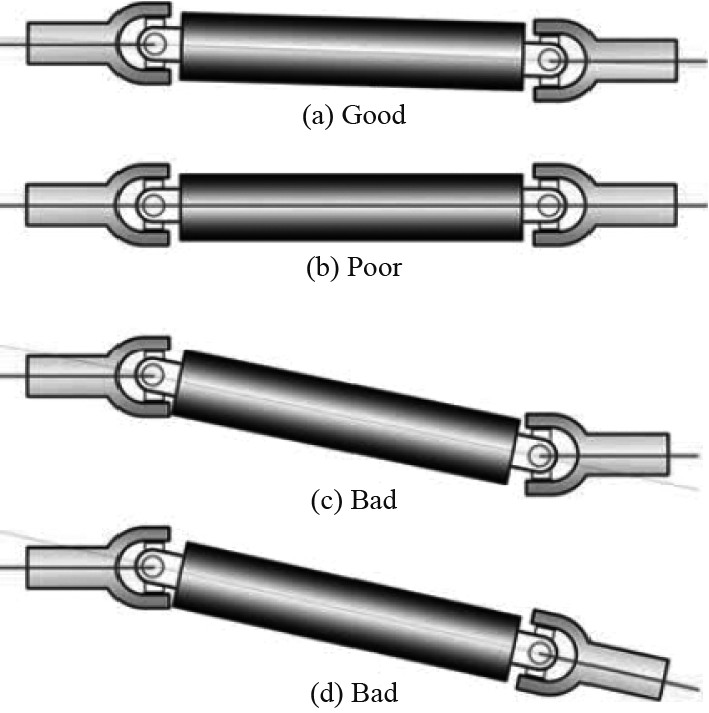
1.5 驱动轴干涉分析悬架机构采取的是可收放系统,通过不等摆臂的方式设计前悬架,通过改变驱动轴长度实现收放。
半潜式快艇驱动轴和摆臂的长度必须保持一致,后悬架摆臂的连接必须和驱动轴万向节保持在同一平面内,以此保证驱动轴在收放过程中不会出现长度变化。图2为驱动轴在收放过程中的运动范围。
|
图 2 驱动轴位置变动示意图 Fig. 2 Schematic diagram of drive shaft position change |
考虑到波浪是一种随机性运动,很难在模型上对其进行全面系统的表达,因此分别研究平均波浪速度和脉动波浪速度对船舶的影响。采用Rankine源与有限差分相结合进行波浪载荷计算,并将假定变量波浪在空间和时间上进行内线性变化,从而探讨波浪载荷差分求解运动方程和动力方程。
2.1 平均波浪速度指数定律确定平均波浪速度计算表达式如下:
| $ v\left( h \right) = v\left( {{h_0}} \right) \times {\left( {\frac{h}{{{h_0}}}} \right)^\alpha } \text{。} $ |
其中:V(h)为高度为h处的波浪速度;h为距离地面的高度;h0为相对于海平面的高度;V(h0)为相对于海平面高度为h0处的波浪速度。
2.2 脉动波浪速度脉动波浪可以看做是一个三维的波浪流,脉动波浪场通常可以分为3个方向,分别是纵向、横向以及垂向。常见的波浪速度功率谱模型主要有Davenport谱、Kaimal谱和Von Karman谱3种波浪速度功率谱模型。
Davenport波浪速度谱是一种不随高度变化的水平脉动波浪速度功率谱,其函数表达式如下:
| $ \frac{{n}{S}_{{n}}({n})}{4K{{v ¯}}_{\text{10}}{}^{2}}=\frac{{{x}}^{2}}{(1+{{x}}^{2}{)}^{4/3}}{x}=1200\frac{{n}}{\bar v_1} \text{。} $ |
其中:n为脉动波浪频率;K为地面粗糙度系数。
Kaimal波浪速度谱数学表达式如下:
| $ S{n}({z},n)=\frac{200{u}_{0}^{2}x}{n{(1+50)}^{5/3}},{u}_{0}^{2}=K{\overline{v}}_{10}{}^{2},x=\frac{nz}{{\overline{v}}_{z}} \text{。} $ |
其中:
Von Karman波浪速度谱表达式如下:
| $ S{n}({z}\text{,}n)=\frac{4{\sigma }_{{u}}^{2}{f}}{n{(1+70.8{{f}}^{2})}^{5/6}} \text{,} $ |
| $ {f}=\frac{{n}L{u}({z})}{{{v ¯}}_{{z}}}\text{,}L({z})=1000 \left(\frac{{z}}{30}\right)^{0.5} \text{。} $ |
半潜式快艇叶片受到的波浪载荷可以通过叶素理论以及动量理论求得。当波浪通过叶轮表面时,在叶轮前后会产生压力差,导致波浪速度的变化。由能量守恒定律,波浪速度差异造成的能量损失其中一部分就转变成了机械能。
叶素理论数学模型如下:
| $ V = (1 - a){V_0} \text{,} $ |
| $ P = 2\rho A{V_0}a{(1 - a)^3} \text{。} $ |
式中:V为叶轮盘面上的波浪速度;V0为上游波浪速度。由此推导得出作用在叶轮上的推力T,如下式:
| $ T = 2\rho A{V_0}a(1 - a) \text{,} $ |
无量纲的功率系数和推力系数分别如下:
| $ {C_P} = \frac{P}{{\left(\dfrac{1}{2}\rho AV_0^3\right)}} = 4a{(1 - a)^2} \text{,} $ |
| $ {C_T} = \frac{T}{{\left(\dfrac{1}{2}\rho AV_0^2 \right)}} = 4a(1 - a) \text{。} $ |
假定一个叶轮的半径为r,则该叶轮产生的推力dT如下式:
| $ {\rm{d}}T = \frac{1}{2}\rho {W^2} + ({C_L}\cos \varphi + {C_D}\sin \varphi )c{\rm{d}}r \text{。} $ |
其中:
| $ {C_L} = L/\left(\frac{1}{2}\rho {V^2}S\right) \text{,} $ |
| $ {C_D} = D/\left(\frac{1}{2}\rho {V^2}S\right) \text{。} $ |
半潜式快艇所处的工作环境非常特殊,在工作期间会受到来自风、波浪,以及海冰各种外界载荷的作用。由于半潜式快艇在运行的过程中通常航速都很高,整体无论是材料选择还是内部配置零件都可以视为一种柔性结构,在受到外界波浪载荷作用时,其结构必定会因承载较大的波浪冲击而发生较大振动。
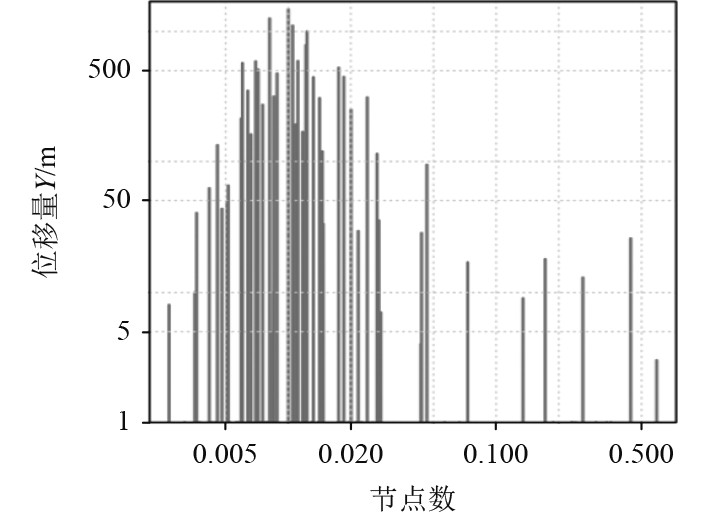
本文对半潜式快艇在波浪载荷作用下的瞬态动力学展开分析,基于Rankine源方法计算出波浪载荷的6个分量Fx、Fy、Fz、Mx、My、Mz施加在半潜式快艇顶部的质量点。与此同时,由于半潜式快艇结构庞大,零件众多,大型零部件之间都是采用焊接的方式进行对接,所以在焊接位置最容易产生疲劳损伤。因此在半潜式快艇受到波浪载荷单独作用时,观测出艇顶的整体位移最大,在Ansys上找到该位置为节点50001处,提取出该节点在3个方向上的位移分量数据,不同节点位移分量对比如图3所示。
|
图 3 不同节点位移分量对比 Fig. 3 Comparison of displacement components at different nodes |
通过观察在3个方向上的位移对比,可知在波浪载荷单独作用下经过0.5个节点后,Y方向的位移也在5 m范围以内,而X方向的位移量要比其他2个方向位移量大很多,这就说明在波浪载荷的作用下,对艇顶造成的位移主要是以X轴方向为主。
3 基于Rankine源方法半潜式快艇有限元建模建模过程中基于Rankine源方法对半潜式快艇的轮毂部分等效成一个质量点,用MSS21单元进行模拟;半潜式快艇塔架结构采用Shell163壳单元进行建模,用这种方法建模能很好模拟半潜式快艇塔架的真实结构。最终利用Ansys软件建立半潜式快艇有限元模型。
3.1 模态分析基于Rankine源方法对半潜式快艇模型进行模态分析,得到半潜式快艇模型前6阶的固有频率如表3所示。
|
|
表 3 半潜式快艇前6阶固有频率 Tab.3 The first six natural frequencies of a semi submersible speedboat |
半潜式快艇的阻尼比取值为5%。将结构的前2阶固有频率单位由角频率转化为Hz,得到质量矩阵系数α=0.0399,刚度矩阵系数β=0.0323。
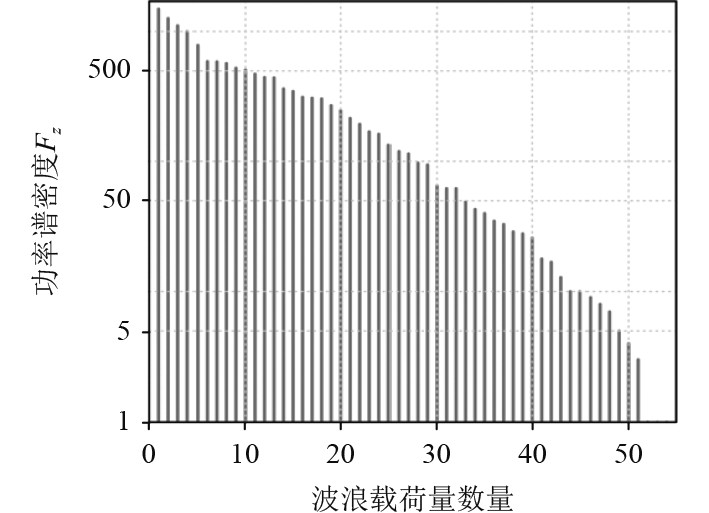
3.3 谱分析的方法与验证将计算得到的波浪载荷进行傅里叶变化,得到波浪载荷分量的功率谱密度函数如图4所示。
|
图 4 波浪载荷Fz功率谱密度函数 Fig. 4 Wave load Fz power spectral density function |
将波浪载荷的6个分量以及风载荷共同进行动力学分析就可以得到热点应力的功率谱密度函数。对半潜式快艇结构施加单位载荷进行谐响应分析,得到波浪载荷以及风载荷的传递函数。考虑当风、波浪载荷互不相关时的情况,此时风、波浪载荷联合作用下的最大应力功率谱密度函数求解公式如下:
| $ S\sigma (w) = {\left| {{H_{{\text{wave}}}}{\text{(w)}}} \right|^2}{S_{{\text{wave}}}}{\text{(w)}} + {\left| {{{\text{H}}_{{\text{wind}}}}{\text{(w)}}} \right|^2}{S_{wind}}(w) \text{。} $ |
可得节点11304处以及节点32619的最大主应力功率谱密度函数。结合频域疲劳分析理论,分别采用窄带近似方法、Wiesching-Light、Oritiz-Chen、Lutes-Lason方法计算疲劳损伤,并且将疲劳损伤结果与时域内进行的双载荷作用下的疲劳损伤结果进行对比,计算误差公式如下:
| $ \delta = \frac{{{D_{\text{f}}} - {D_{\text{t}}}}}{{{D_{\text{t}}}}} \times 100\text{%} 。$ |
本文基于Rankine源方法探究半潜式快艇的波浪载荷,为提升半潜式快艇的安全性能,在设计方案上提供一种计算新思路。
| [1] |
于小伟, 姜涛, 罗瑞锋. 新型浮式平台波浪载荷计算方法研究与应用[J]. 船舶与海洋工程, 2022, 38(1): 6-7. YU Xiao-wei, JIANG Tao, LUO Rui-feng. Research and application of new calculation method for wave loads on floating platforms[J]. Ship and Ocean Engineering, 2022, 38(1): 6-7. |
| [2] |
王澄, 张高峰, 袁昌耀, 等. 基于计算流体力学的船舶风载荷计算方法分析[J]. 天津理工大学学报, 2021, 037(2): 21-26. WANG Cheng, ZHANG Gao-feng, YUAN Chang-yao, et al. Analysis of calculation method for ship wind load based on computational fluid dynamics[J]. Journal of Tianjin University of Technology, 2021, 037(2): 21-26. DOI:10.3969/j.issn.1673-095X.2021.02.005 |
| [3] |
陆泽华, 曹旭, 李传庆. 基于数值计算的船舶波浪增阻和运动响应预报方法论证[J]. 上海船舶运输科学研究所学报, 2022, 45(4): 13-19+32. LU Ze-hua, CAO Xu, LI Chuan-qing. Demonstration of forecasting method for ship wave resistance and motion response based on numerical calculation[J]. Journal of Shanghai Institute of Shipping Science, 2022, 45(4): 13-19+32. DOI:10.3969/j.issn.1674-5949.2022.04.003 |
| [4] |
杨云涛, 朱仁传, 高慧. 波浪中航行船舶水动力和运动分析的Rankine源高阶面元法研究[J]. 中国造船, 2022, 63(1): 14-27. YANG Yun-tao, ZHU Ren-chuan, GAO Hui. Research on the Rankine source high-order surface element method for hydrodynamic and motion analysis of ships sailing in waves[J]. China Shipbuilding, 2022, 63(1): 14-27. DOI:10.3969/j.issn.1000-4882.2022.01.002 |
| [5] |
杨云涛, 朱仁传, 陆安, 等. 基于频域高阶Rankine源法的有航速船舶斜浪中六自由度运动数值计算研究[J]. 船舶力学, 2022, 26(11): 1668-1679. YANG Yun-tao, ZHU Ren-chuan, LU An, et al. Numerical calculation of six degrees of freedom motion in oblique waves of ships with speed based on high-order Rankine source method in frequency domain[J]. Ship Mechanics, 2022, 26(11): 1668-1679. DOI:10.3969/j.issn.1007-7294.2022.11.010 |
| [6] |
崔金龙, 李元奎, 索基源, 等. 基于改进A^(*)算算法的船舶航向航速协同优化方法[J]. 大连海事大学学报, 2022, 48(4): 10-12. CUI Jin-long, LI Yuan-kui, SUO Ji-yuan, et al. Collaborative optimization method for ship course and speed based on improved A^(*) algorithm[J]. Journal of Dalian Maritime University, 2022, 48(4): 10-12. |
| [7] |
吕向琪, 张志恒, 张新曙, 等. 基于频域Rankine面元法的船舶耐波性计算和分析[J]. 海洋工程, 2023, 41(1): 68-81. LV Xiang-qi, ZHANG Zhi-heng, ZHANG Xin-shu, et al. Calculation and analysis of ship seakeeping based on frequency domain rankine surface element method[J]. Ocean Engineering, 2023, 41(1): 68-81. DOI:10.16483/j.issn.1005-9865.2023.01.008 |
 2023, Vol. 45
2023, Vol. 45
