潜艇推进效率关系到潜艇最大航速和续航力,是潜艇重要的性能指标。国内外学者主要通过对螺旋桨进行优化设计或者在桨后安装毂帽鳍的方式来提高螺旋桨推进效率。但是随着目前螺旋桨设计的不断优化,对潜艇螺旋桨的推进效率的提升已达到瓶颈,需要寻求新的解决方案。
目前潜艇采用的是尾舵位于螺旋桨前方的布局方式,尾舵离螺旋桨较近,对潜艇螺旋桨水动力性能有重要影响。20世纪80年代末,美国国防高级研究计划局(DARPA)提出了SUBOFF项目,美国Taylor水池对项目中的SUBOFF模型艇进行了系统的水动力和流场测试试验,为研究潜艇流场和水动力性能提供了丰富的试验数据[1]。潜艇尾舵通常采用十字型或X型的布局方式,根据舵和稳定翼提供的功能差异可分为全动舵与组合舵[2]。当潜艇在水下航行时,潜艇尾舵与周围的水介质发生相对运动,产生造成流体粘性停滞和流动分离的“阻塞效应”,在潜艇尾部形成了复杂的尾流场,学者们为此展开了尾舵优化设计的研究。梁秋凤等[3-4]基于STAR-CCM+软件,将十字舵的稳定翼和转动舵在空间上分离,设计了能够有效减小尾流场不均匀度的X舵+稳定翼尾舵形式。翟朔等[5-7]对SUBOFF潜艇模型的尾舵进行了转动舵和稳定翼的共翼型设计,并分别用CFD方法和模型试验方法得到了潜艇尾流场数据,得出了共翼型舵能够明显消减舵翼结合部涡流,可以增大舵后尾流低速区流体速度,能够有效提高潜艇尾流场品质的结论。Jin等[8]以SUBOFF模型为研究对象,采用SSG雷诺应力湍流模型,将艇体与尾舵前端直角连接处改为3种不同的圆角形式,发现凸型圆角能够有效减小马蹄涡的产生和强度,并能够减小螺旋桨盘面进流周向不均匀性。
目前主要是从改善螺旋桨进流品质出发对潜艇尾舵进行优化设计,以降低桨盘面流场的不均匀性。
潜艇采用的尾舵大多数为对称舵,来流经过对称舵后在局部范围内会存在一定的周向速度,但周向速度的大小与轴向速度相比是小量,且如果将各半径处的流场在周向上进行平均处理,得到的流场中周向速度分量基本为0,与轴向速度相比可以忽略不计,而螺旋桨是通过旋转的方式产生推力,螺旋桨尾流中会存在明显的周向诱导速度与轴向诱导速度,其形成的动能是螺旋桨能量损失的主要部分。而对称舵后尾流的周向速度分量很小,导致螺旋桨尾流中的周向诱导速度较大,螺旋桨尾流中周向诱导速度引起的动能损失也会较大,对螺旋桨推进效率产生不利影响。除此之外,对称舵在艇体中心轴线上产生的力矩基本为0,使得艇体上存在较大的不平衡扭矩。
针对潜艇的尾流场特性,本文以SUBOFF潜艇模型为研究对象,在原有常规舵基础上,设计一种用于提高螺旋桨推进效率的新型扭曲舵。采用数值计算的方法对分别安装常规舵和扭曲舵时潜艇水动力性能进行计算,分析扭曲舵对潜艇螺旋桨推进效率的影响。
1 研究对象为分析潜艇扭曲尾舵对潜艇水动力性能的影响,基于SUBOFF潜艇模型,在原有常规对称尾舵的基础上设计一种扭曲舵。SUBOFF模型艇体总长L为4.356 m,艇体最大半径Rmax为0.254 m,计算螺旋桨为某7叶大侧斜螺旋桨,桨直径d为0.207 m,旋向为左旋,安装在模型艇桨盘面x=4.26 m处,全附体潜艇模型如图1所示。

|
图 1 SUBOFF潜艇模型 Fig. 1 Model of SUBOFF submarine |
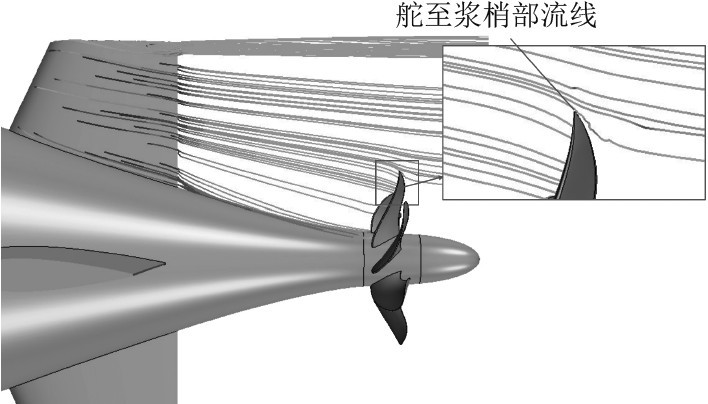
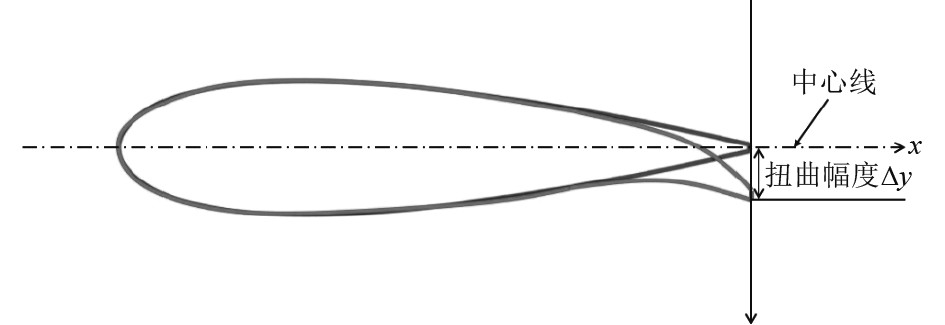
SUBOFF潜艇模型中的尾舵为十字全动舵,本文中扭曲舵是在潜艇原有尾舵的基础上根据螺旋桨旋向将舵进行扭曲设计,先根据自航时潜艇尾舵到螺旋桨梢部的流线确定舵扭曲展向起始位置,流线形状如图2所示,常规舵如图3所示。从扭曲展向起始位置开始向内半径位置直到舵根部即为发生扭曲的扭曲范围,在发生扭曲的展向范围内通过改变各剖面拱度的方式,使剖面的形状发生改变,改变后剖面的拱度线不再是沿纵向的直线,整个舵呈现出扭曲的形态。定义各展向位置上扭曲后剖面与原舵对应剖面在横向上的最大偏移量为该剖面处的扭曲幅度
|
图 2 潜艇尾舵至螺旋桨梢部流线示意图 Fig. 2 Flow line diagram from submarine tail rudder to propeller tip |
|
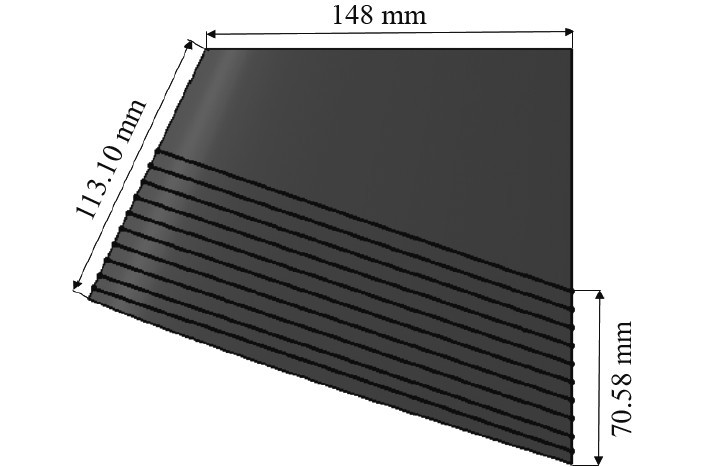
图 3 常规舵 Fig. 3 Conventional rudder |
|
图 4 单个舵叶剖面扭曲幅度示意图 Fig. 4 Schematic diagram of distortion amplitude of single rudder blade section |

|
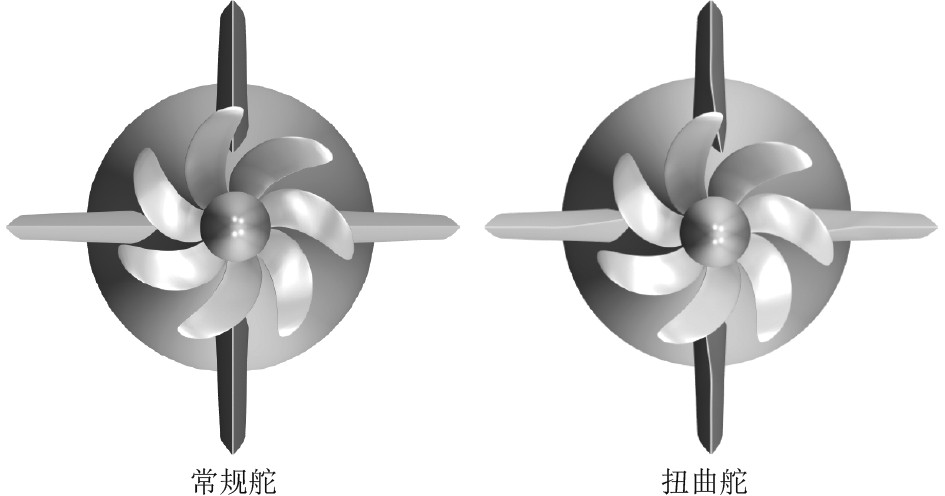
图 5 扭曲舵 Fig. 5 Twisted rudder |
|
图 6 不同尾舵在艇体尾部安装示意图 Fig. 6 Installation diagram of different stern rudders at the stern of the hull |
在流体不可压缩的条件下,流场的连续方程和动量方程为:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0,$ | (1) |
| $ \rho \frac{{\partial \left( {{u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial P}}{{\partial {x_j}}} + \rho {g_i} + \rho \frac{\partial }{{\partial {x_j}}}\left( {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \rho \overline {{{u'}_i}{{u'}_j}} } \right) 。$ | (2) |
式中:
为了将上述方程封闭起来,必须引入合适的湍流模型。
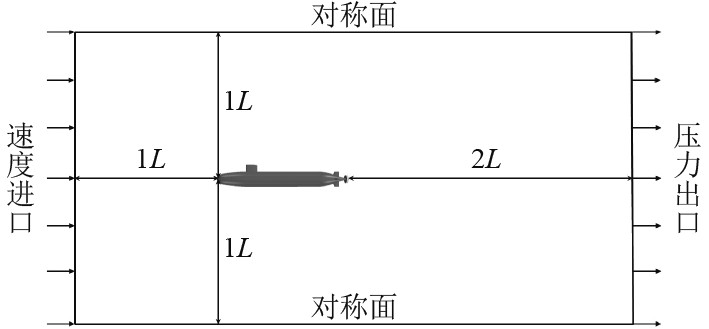
为了模拟潜艇模型周围的流场,构建一个半径为1L的圆柱体形流体区域,将计算域划分为外域和螺旋桨所在的旋转域。计算外域外边界为圆柱体表面,艇首前侧的外域边界设置为速度进口,距离艇首1L距离;艇尾后侧的外域边界设置为压力出口,距离艇尾2L距离;外域侧面设置为对称面,其中L为艇长。计算外域内边界为艇体模型表面,采用无滑移壁面条件,计算外域大小如图7所示。
|
图 7 计算外域大小示意图 Fig. 7 Schematic diagram of calculating external domain size |
旋转域是包括螺旋桨在内的圆柱体形流体区域,半径为0.125 m,轴向长度为0.065 m。旋转域外边界设置为外域和旋转域的交界面,内边界为螺旋桨表面,壁面条件同艇体。在CFD模拟中,定常计算时,旋转域旋转采用MRF方法进行模拟;非定常计算时,旋转域旋转采用滑移网格法进行模拟。
计算坐标系采用笛卡尔坐标系,遵循右手定则,以潜艇首部顶点为坐标原点,x轴正方向由艇首指向艇尾,y轴正方向指向艇体右舷,z轴以垂直向上为正。
尾舵的存在会影响流体的连续性,造成流体粘性停滞和分离的“阻塞效应”,导致其周围流场变化剧烈,对潜艇螺旋桨进流和尾流场品质有一定影响,另外本文所采用的SUBOFF模型还包括了指挥台围壳。为准确预报流场,使潜艇尾流场更加符合实际情况,在上述区域划分的基础上,采用精细化结构网格对计算区域进行网格划分,对指挥台围壳、尾舵、螺旋桨和桨-舵附近区域进行加密。为了保证网格的周期性,螺旋桨所处的旋转域可看作,由单片桨叶所在的单通道网格周期性旋转得到的全通道网格。由于扭曲舵是在原有常规舵的基础上改进设计的,其与常规舵展长相同,面积接近,所以更换尾舵并不会对网格总数造成太大影响,无桨时2种尾舵形式的潜艇网格总数都是在1 405万左右,加装螺旋桨后,网格总数在2 488万左右,其中由于加装了螺旋桨。为了保证网格划分的质量以及节点数量与无桨潜艇模型网格尽量一致,静止域网格总数增加至1 581万左右,旋转域网格总数为907万左右,具体网格划分如图8所示。

|
图 8 网格划分 Fig. 8 Gridding diagram |
自航试验是预报分析潜艇各种快速性和尾流场特性指标的重要手段。拖航试验[10]是自航试验前的必要环节,目的是验证计算方法的适用性及得到潜艇不带桨时的拖航阻力,为进一步分析潜艇尾流场及推进性能提供数据参考。
结合不同湍流模型,在网格划分的基础上对SUBOFF潜艇模型进行拖航试验模拟。由于拖航时,模型并未安装螺旋桨,不需要模拟螺旋桨的旋转运动,所以采用定常的方法。在潜艇保持直航且来流速度VS= 3.050 4 m/s的条件下,对全附体SUBOFF模型艇进行数值计算,得到采用不同湍流模型的潜艇拖航阻力。与试验[11]数据对比,结果如表1所示。
|
|
表 1 不同湍流模型潜艇拖航总阻力对比 Tab.1 Comparison of total towing resistance of submarine with different turbulence models |
可以看出,采用SST
|
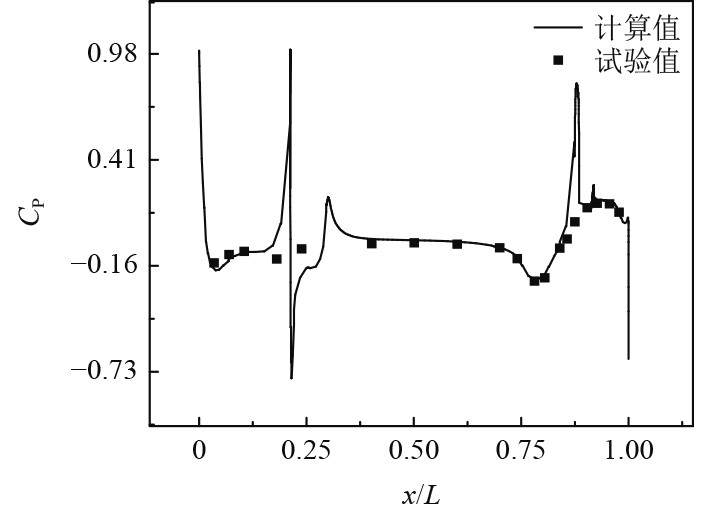
图 9 中纵剖线上部分压力系数分布 Fig. 9 Partial pressure coefficient distribution on the middle longitudinal section line |
压力系数公式为:
| $ {C_P} = \frac{{p - {p_0}}}{{1/2\rho V_{\text{S}}^2}}。$ | (3) |
式中:
由图9可知,x/L处于0.212~0.3和0.874~0.919之间时潜艇表面出现了明显的高压区和低压区。这是因为潜艇在航行时,由于指挥台围壳和尾舵的存在,使得潜艇线型发生突变,流体在两处区域会受到阻碍,导致流体分离,使得两侧压力分布变化剧烈。而试验中采用的是不带任何附体的裸艇体模型,得到的潜艇其他部分表面压力系数与计算值基本吻合,说明上述数值计算方法结合SST
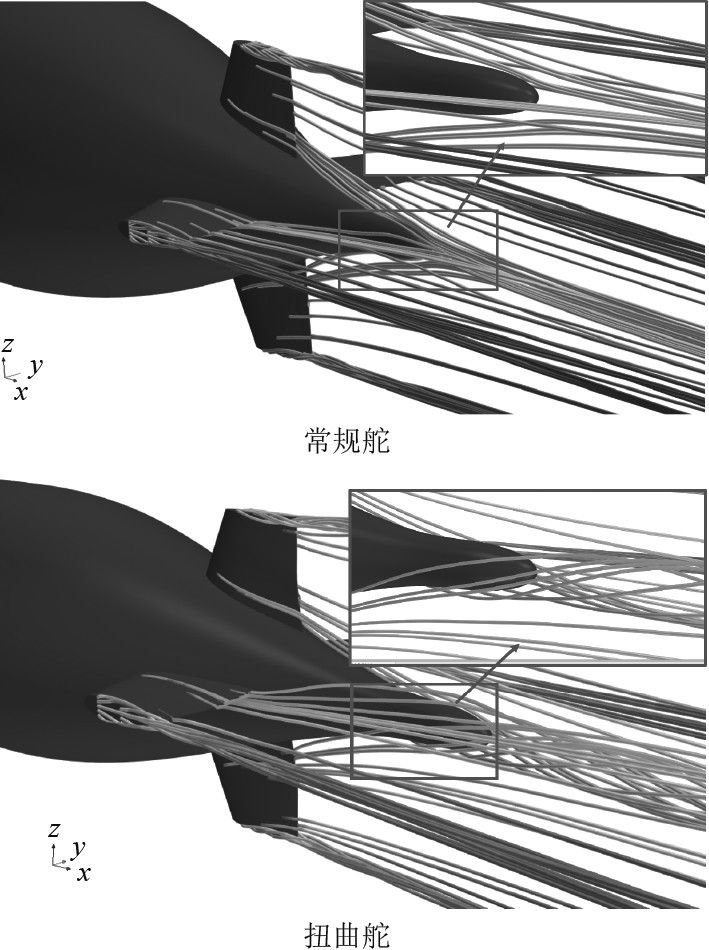
对无桨时不同尾舵形式潜艇进行拖航试验模拟,得到带常规舵潜艇拖航阻力为104.558 N,带扭曲舵潜艇拖航阻力为105.502 N。图10为无桨时不同尾舵形式潜艇舵后流线图,可以看到来流经过常规舵后,其形成的尾流中周向速度分量相对于轴向速度来说占比很小,可以忽略不计。而来流经过扭曲舵后形成的尾流中有一定的周向速度分量占比,并在舵后尾流场中形成了与本文采用的螺旋桨旋向相反的预旋流,这有利于螺旋桨吸收尾流中的周向能量,降低周向诱导速度引起的动能损失。
|
图 10 无桨时不同尾舵形式潜艇舵后流线图 Fig. 10 Flow line behind rudder of submarine with different tail rudders without propeller |
对安装螺旋桨和常规舵的潜艇进行自航试验模拟,计算先采用定常计算的结果作为初始值,采用非定常方法计算,螺旋桨旋转采用滑移网格法进行模拟,通过改变螺旋桨的工作转速
|
|
表 2 不同尾舵形式潜艇水动力参数对比 Tab.2 Hydrodynamic parameters of submarine with different tail rudders |
表中,
在螺旋桨工作转速为16.842 r/s时,螺旋桨推力与潜艇总阻力仅相差0.19%,可以认为带常规舵潜艇基本达到自航状态。从表2可以看出,在相同转速下,相比于带常规舵潜艇,带扭曲舵潜艇的艇体总阻力略微升高,螺旋桨的推力和扭矩皆有较大幅度的提升。由于模拟中潜艇是直航并未打舵角,常规舵实际上并不会对艇体中心轴线产生扭矩,所以计算出现的尾舵扭矩是由CFD计算的误差带来的,其数值很小可以忽略不计。
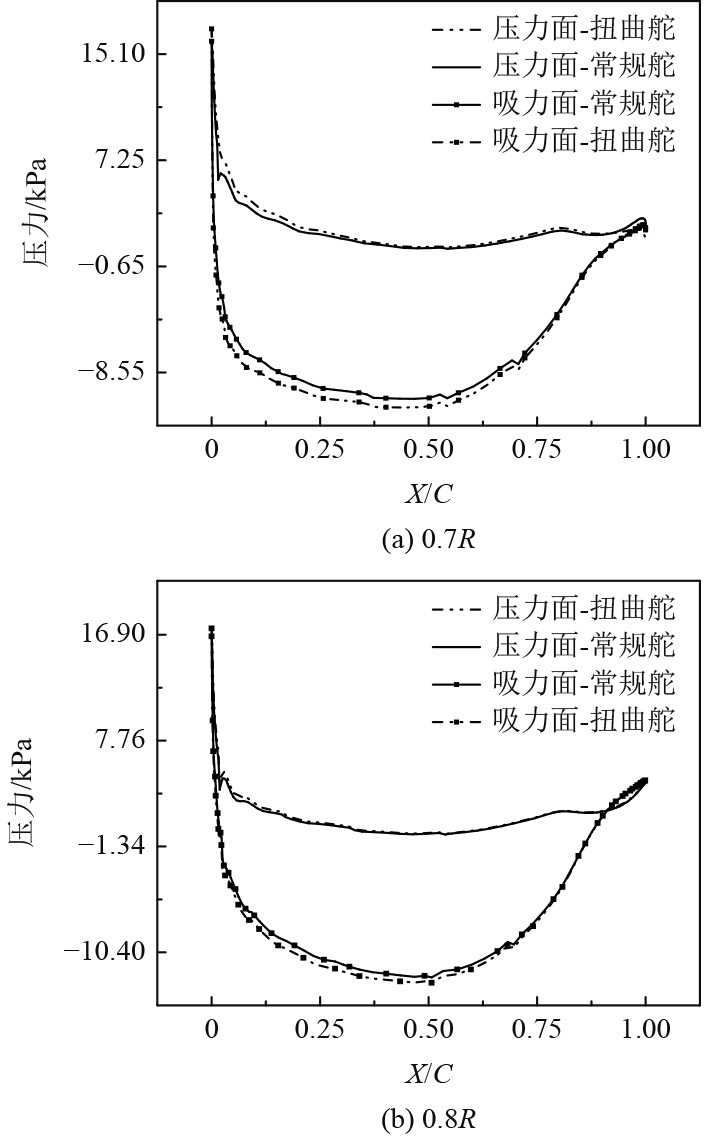
待计算稳定后,当2种尾舵形式潜艇的螺旋桨旋转到同一位置时,对潜艇的水动力性能进行对比分析。R为螺旋桨半径,图11为2种尾舵形式潜艇同一片桨叶在0.7 R和0.8 R半径截面处的压力分布对比,可以看到带扭曲舵潜艇的螺旋桨吸力面压力相对于带常规舵潜艇较低一些,压力面压力又明显高于后者。这是由于来流经过扭曲舵后形成了预旋流,在预旋流流至螺旋桨桨盘面时,其与螺旋桨叶片所成攻角会相应地增大,螺旋桨相对旋转速度提高,这就导致了螺旋桨叶片的负荷增大,需要用来克服由于螺旋桨旋转本身产生的不平衡扭矩所做的功也就越大。而因此流过螺旋桨工作区域的预旋流会被螺旋桨充分吸收利用,螺旋桨尾流中的诱导速度也会因为螺旋桨的抽吸作用相应地减小,螺旋桨吸力面压力降低,压力面压力增大,两侧的压力差增大。
|
图 11 不同尾舵形式潜艇螺旋桨压力分布 Fig. 11 Pressure distribution of submarine propeller with different stern rudders |
上述分析中带扭曲舵潜艇并没有达到自航状态,其螺旋桨的推力明显大于艇体总阻力,而为了比较2种尾舵形式对潜艇螺旋桨推进效率的影响,需要降低螺旋桨工作转速,使带扭曲舵潜艇也达到自航状态。对分别安装2种尾舵形式的潜艇在相同航速下自航时的水动力性能进行数值计算,对比安装2种尾舵形式潜艇的推进效率成分。调整螺旋桨工作转速后达到自航状态的带扭曲舵潜艇水动力参数如表3所示。
|
|
表 3 自航状态下扭曲舵潜艇水动力参数 Tab.3 Hydrodynamic parameters of submarine with twisted rudder under self-propelled |
对比表2与表3的水动力参数可以看出,潜艇尾舵形式改为扭曲舵后,尾舵阻力与潜艇总阻力不会增加太多。相比于带常规舵潜艇,带扭曲舵潜艇的尾舵由于部分扭曲,本身就会对艇体中心轴线产生一定的扭矩,且扭矩方向与螺旋桨产生的水动力扭矩方向相反,使潜艇整体的不平衡扭矩有所降低。
在螺旋桨推力与艇体阻力平衡时,螺旋桨的推进效率计算式为:
| $ \eta = \frac{{{V_{S}}{R_0}}}{{2{\text{π}} nQ}}。$ | (4) |
在CFD计算当中,艇体阻力
| $ \eta = \frac{{{V_{\text{S}}}({R_0} + T - {R_s})}}{{2{\text{π}} nQ}}。$ | (5) |
螺旋桨推力系数
| $ {K_T} = \frac{T}{{\rho {n^2}{D^4}}} ,$ | (6) |
| $ {K_Q} = \frac{Q}{{\rho {n^2}{D^5}}} 。$ | (7) |
其中:
|
|
表 4 不同尾舵形式潜艇推进效率成分对比 Tab.4 Comparison of propulsion efficiency components of submarine with different tail rudders |
结合表2~表4数据看,在螺旋桨保持不变且航速相同的工况下,尾舵由常规舵改为扭曲舵后,潜艇艇体阻力基本不变,航行达到自航点所需要的转速减小。
本文通过CFD方法,对分别安装常规舵和扭曲舵2种尾舵形式的潜艇进行自航试验模拟,并且比较了2种尾舵形式对潜艇水动力性能和螺旋桨推进效率的影响。通过对计算结果进行对比分析,总结出以下结论:
1)潜艇尾舵形式改为扭曲舵后会使来流经过舵后形成旋向与螺旋桨旋向相反的预旋流,有效改善了螺旋桨进流,预旋流中的周向速度分量占比提升,有利于降低螺旋桨尾流中周向诱导速度引起的动能损失,且预旋流与螺旋桨叶片形成的攻角更大,增大了桨叶的相对旋转速度,周向能量得以充分利用,使螺旋桨的推进效率提高了约8.22%。
2)在螺旋桨保持不变且航速相同的工况下,尾舵由常规舵改为扭曲舵后,对潜艇的阻力影响不大,航行潜艇达到自航点所需的螺旋桨转速和收到功率下降,有利于提高潜艇最大航速,提高续航力。且扭曲舵可以产生与螺旋桨转动方向相反的扭矩,这部分扭矩可使潜艇整体的不平衡扭矩降低。
| [1] |
GROVES N C, HUANG T T, CHANG M S. Geometric characteristics of DARPA SUBOFF models[R]. David Taylor Research Center, 1989.
|
| [2] |
王京齐, 施生达. 现代潜艇尾操纵面的发展状况[J]. 舰船科学技术, 2007(1): 33-36+40. |
| [3] |
梁秋凤, 叶金铭, 张露, 等. 潜艇舵翼分离型尾操纵面水动力及尾流场研究[J]. 舰船科学技术, 2021, 43(21): 33-38. |
| [4] |
曹植珺, 肖昌润, 李士强, 等. X舵与十字舵潜艇稳定性对比分析[J]. 舰船科学技术, 2021, 43(7): 51-55. |
| [5] |
翟朔, 刘志华. 艇尾共翼型舵水动力和尾流场特征的数值计算研究[J]. 中国造船, 2019, 60(1): 109-119. DOI:10.3969/j.issn.1000-4882.2019.01.012 |
| [6] |
刘志华, 熊鹰, 叶青. 共翼型舵水动力特性的模型试验与数值模拟[J]. 哈尔滨工程大学学报, 2018, 39(4): 658-663. |
| [7] |
翟朔, 刘志华. 局部等厚的共翼型舵对潜艇尾流场优化效果研究[J]. 推进技术, 2020, 41(7): 1660-1669. |
| [8] |
Jin Z, Wang P, Xia H, et al. Validation of Numerical Simulation on the Flow Field of Submarine with Various Types of stem appendages[C]// Oceans 2018 MTS/IEEE Charleston. IEEE, 2018.
|
| [9] |
叶金铭, 张凯奇, 于安斌. 基于STAR-CCM+的全附体潜艇尾流场数值分析[J]. 海军工程大学学报, 2017, 29(4): 53-58. |
| [10] |
韩聪. 基于CFD的船用螺旋桨前置预旋定子优化设计研究[D]. 上海: 上海交通大学, 2018.
|
| [11] |
HUANG T, LIU H L, GROVES N, et al. Measurements of flows over an axisymmetric body with various appendages in a wind tunnel: the DARPA SUBOFF experimental program[C]// Proceeding of 19th Symposium on Naval Hydrodynamics. Seou, 1992.
|
 2023, Vol. 45
2023, Vol. 45
