现代大型水面舰艇多在舷侧设置多舱防护结构来抵御反舰武器的破坏,即在舷侧设置多层液舱和空舱,其中液舱主要用来抵御战斗部及破片的侵彻[1]。而杆状弹在二战之后便广泛应用于各种军事武器,杆状弹主要凭借其高密度金属弹芯及大长径比的特点,依靠动能穿透防护装甲,因此杆状弹多用于反坦克武器及反舰武器。爆炸成型弹丸是杆状弹的典型代表,凭借其直径大、呈长杆式、连续性好、强度高、抗干扰能力和侵彻能力强等优点,成为海上反舰武器的主要选择[2]。爆炸成型弹丸由于其通过爆轰作用生成高速弹体,其能量密度和侵彻能力远大于普通弹体[3-4],普通的舰船舷侧液舱防护结构不能抵御EFP弹的高速侵彻[5-6]。而杆状弹在侵彻舰船时不可避免的会接触加筋板等障碍物,使弹体的姿态角度等弹道特性发生改变,进而影响其侵彻能力[7]。鱼雷及射弹在攻击水下目标时通常也是带攻角入水,因此研究杆状弹非理想入水对舰船的防护有重要意义。
国内外学者都对杆状弹理想情况下入水展开了大量研究。杨莉[8]通过EFP侵彻含水介质实验,表明水介质对EFP有一定的侵蚀作用,且弹丸初始形状对侵彻威力有较大影响。许通通[9]用AUTODYN建立聚能侵彻体侵彻水介质,发现由于EFP的质量集中,水介质对其的平均衰减速度最大。在杆状弹低速入水情况下,Chen[10-12]通过试验发现弹体垂直入水或倾斜入水下都会发生弹体的翻滚与弹道偏转现象;李天雄[13]用数值仿真的方法验证了对称弹体垂直入水同样会发生弹道偏转;Mojtaba[14]则考虑空腔形态的瞬态模型来建立完整的圆柱体弹丸入水模型。杆状弹高速侵彻时,一般看作是半流体侵彻,Alekseevskii[15]和Tate[16]给出了长杆弹半流体侵彻的理论分析模型。弹体侵彻液舱也是入水研究的重要领域。杆状弹侵彻水箱会产生水锤效应,一般分为冲击阶段、阻滞阶段、空化阶段、穿出阶段,其中冲击阶段产生的冲击波以及空化阶段产生的空化压力载荷是造成水箱结构破坏的主要载荷[17]。仲强[18]通过弹体侵彻水箱试验,并在壁面布置压力传感器研究水锤效应的载荷规律,得到壁面受到的压力载荷时程曲线,发现压力载荷具有多峰性。李典[19-21,24]运用LS-DYNA软件对液舱结构抗侵彻进行数值模拟,在防护效能、载荷特性和耗能机理方面进行分析,发现液舱结构在抗高速侵彻上有良好表现。在弹体非理想侵彻方面,朱珠[22]基于CFD计算建立了大攻角入水弹道模型,能较为准确预测大攻角柱形弹的入水弹道;汪振[23]则用LS-DYNA研究弹体小攻角斜入水,发现正攻角会使弹体产生顺时针的径向载荷,负攻角会使弹体产生逆时针的径向载荷,载荷大小随攻角的增大而增大。
但是上述弹体非理想侵彻研究还仅在低速弹体层面,高速杆状弹的非理想侵彻入水研究很少。因此本文针对杆状弹在侵彻过程中,由于其他原因产生攻角的情况下对于侵彻液舱进行研究。因为现在弹道试验多采用弹道枪或轻气炮,其发射状态均比较理想,无法发射特定攻角的弹体,数值计算可以给与弹体特定的初始状态,因此现在非理想的弹道入水研究大部分采用数值计算。本文采用LS-DYNA建立弹体带攻角入水模型,研究不同攻角下弹体速度、长径比对弹体入水后的剩余特性、空泡形状及弹体姿态的影响。
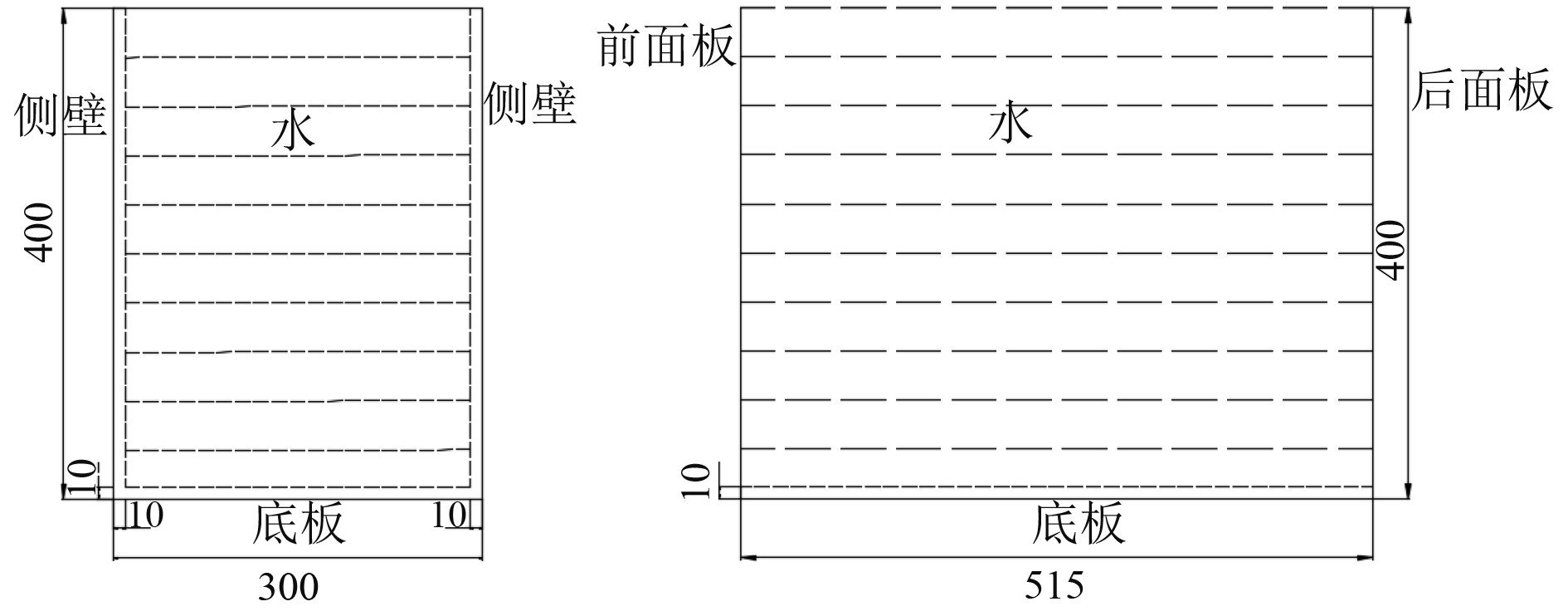
1 数值计算方法及验证 1.1 数值计算模型设计直径12.45 mm、长径比为1.65、3.3、4.95的3种钢制杆状弹,并建立300 mm×400 mm×515 mm的水箱模拟舰船液舱。由于实际舰船中液舱内储水并不注满,所以水箱上侧不封盖,模拟液舱的自由液面。水箱两侧壁厚为10 mm,前面板、背面板厚度为1 mm。
|
图 1 水箱模型 Fig. 1 Model of tank |
子弹网格沿直径方向等分为12份,沿长度方向划分1 mm的网格。子弹速度平行于水平面,即沿z轴方向。在水箱内建立水域,水箱外设置空气域,水域与空气域网格为4 mm,在其中心区域进行网格加密。为了节省计算时间,根据结构与弹道冲击试验的对称性,全部模型均建立1/2对称模型。
1.2 数值计算方法数值计算采用LS-DYNA软件中的流固耦合算法,弹体、水箱等固体结构采用六面体拉格朗日单元,水域与空气域采用欧拉单元,水域与空气域共节点,以实现水介质与空气的流动。采用LAGRANGE_IN_SOLID命令卡片实现结构与流体的耦合。在对称面上设置对称约束,限制其法线方向的位移及非法向方向的旋转。由于重力在弹体入水时不可忽视,所以在欧拉域内用LOAD_BODY命令设置重力场,并设置INITIAL_HYDROSTATIC_ALE命令在水域内定义静水压力,弹体与钢板、水箱的接触设置为ERODING_SURFACE_TO_SURFACE。
水箱及钢板材料均为Q235钢,采用Cowper-Symonds本构模型;弹体材料为45#钢,选用Johnson-cook本构模型;水采用Gruneisen状态方程;空气为无粘性的理想气体,则其状态方程为线性多项式。具体参数如表1~表3所示。
|
|
表 1 Q235钢的材料参数 Tab.1 Material parameters of Q235 |
|
|
表 2 子弹的材料参数 Tab.2 Mechanical parameters of projectile |
|
|
表 3 流体的材料参数 Tab.3 Material parameters of fluid |
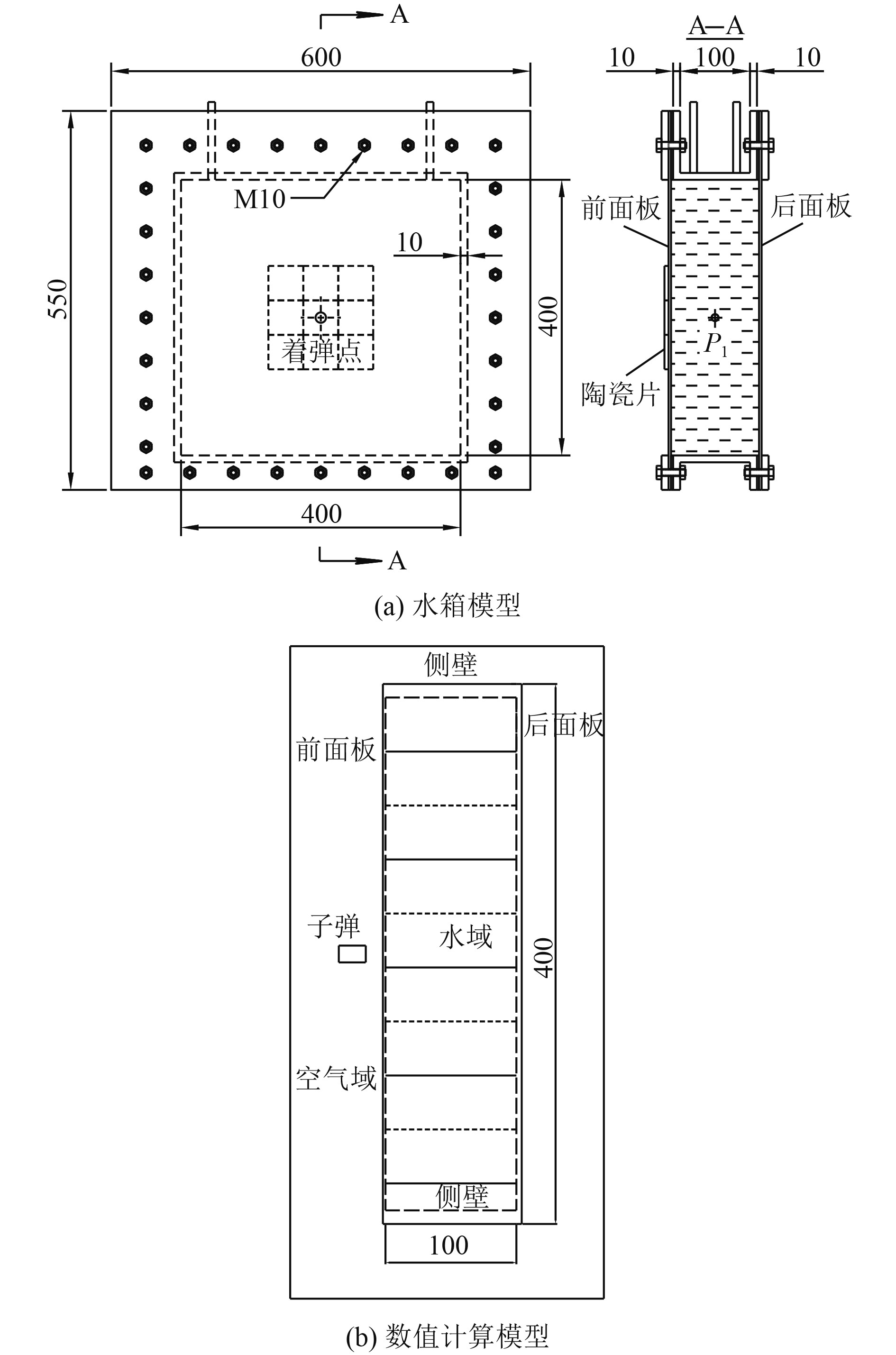
为验证数值计算算法的正确性,根据参考文献[18, 21, 24]建立弹体侵彻充液结构的模型,文献中试验为用直径14.5 mm、高18 mm的45#钢制圆柱平头弹侵彻如图2所示。水箱前后各放置厚度不同的Q235钢板,以不同初速度弹体侵彻厚度配比不同的水箱并测得其剩余速度。
|
图 2 水箱模型及数值计算模型 Fig. 2 Model of tank and numerical calculation |
在LS-DYNA中建立与文献相应的数值计算模型,试验值和数值计算结果如表4所示。可以看出,弹体的剩余速度试验值与数值计算值具有良好的一致性,误差均在10%以内,且弹体呈蘑菇头侵蚀变形,前板鼓胀变形及后板的碟形变形都趋于一致,证明了算法的准确性。
|
|
表 4 试验值与有限元数值比较 Tab.4 The comparison of experiment and simulation result |

|
图 3 前面板和弹体破坏形貌及数值仿真结果 Fig. 3 Damage morphology of front plate and projectile in experiment and numerical simulation |
由于弹体入水后的运动主要受到弹头形状、液体黏度及弹体头尾部压力差的影响。带攻角弹体入水与正侵彻入水速度衰减趋于一致,而弹体姿态却有较大区别,可以分为3个阶段。
1)入水阶段
即是弹体撞击薄钢板及之后的入水开坑阶段。弹体撞击钢板时,由于钢板有水介质的“动支撑”,对弹体速度有最强的衰减;且钢板后水介质为无干扰状态,水介质的阻力较大,此阶段弹尾还在空气中与水介质无接触,弹头则受到钢板及未受扰动的水介质给与的阻力,此时弹体头尾部压力差最大,所以弹体速度基本呈线性快速衰减;而弹体则基本保持弹体初始姿态前行。
2)翻转阶段
此阶段弹体破开水介质,受到水介质的拖拽力,弹体动能转化为弹体变形能、水介质的内能与动能,弹头产生非对称墩粗或蘑菇头状变形,迎流面积增大;同时弹体高速前进造成空化现象,在水箱内形成空腔。此时弹体速度逐渐衰减,水给的作用力减小,导致弹头受到的压力减小,压力差降低,弹体速率呈指数衰减,衰减速率逐渐缓慢。而由于攻角存在使弹体受到合力在非轴向方向,产生转动力矩,弹体在此阶段始终翻转。
3)稳定阶段
当弹体侵彻后期,速度降到一定程度时,其弹头形状基本不发生变化,由于弹头所受压力与弹速成正比,弹速越低,其所受水的压力越小,其弹体头尾部压力差较小,弹体所受阻滞力很小,弹体速度衰减缓慢。而经过翻转,弹体达到翻转达到最大迎流面,则弹体姿态始终在最大迎流面附近轻微转动,基本保持稳定。
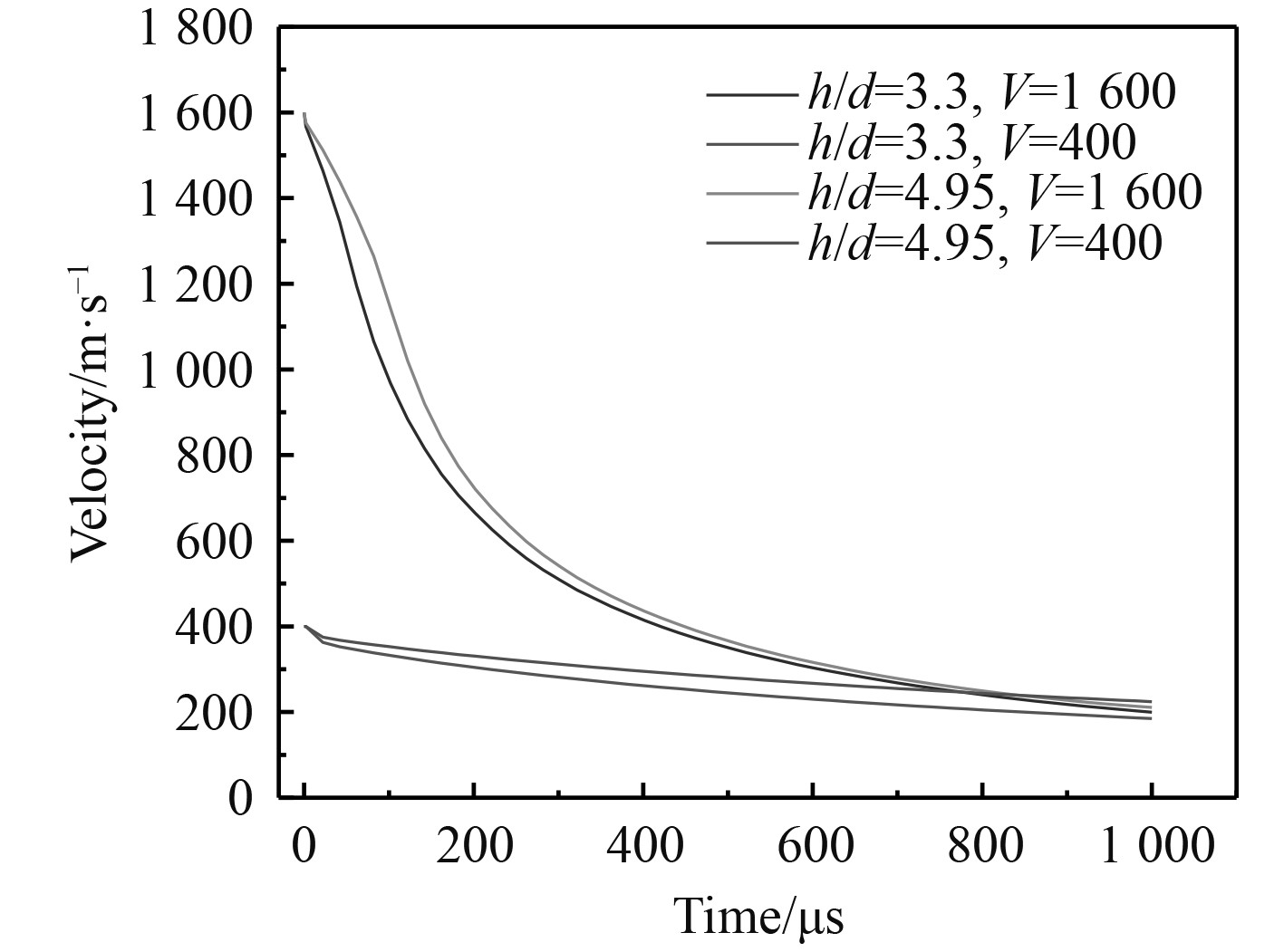
由图4可看出,相同初速度下,长径比较大的弹体入水后速度大于长径比小的弹体,表明长杆弹在侵彻水介质过程中的存速效果也较好。而入水速度越大,水介质的降速效果越好,初始速度较高的弹体与初速低的弹体在入水一段时间后,两者剩余速度基本能趋于一致。这是因为高速弹体入水产生弹体的侵蚀及弹头的墩粗变形,弹体被侵蚀导致弹体质量减小,则其动能也减小,弹头墩粗变形导致弹体迎流面积增大,其所受阻力更大,所以在一段时间后,其速度衰减至与低速弹体相同。
|
图 4 不同长径比弹体入水的速度随时间变化关系(正侵彻) Fig. 4 Relationship between time and velocity with different length-diameter ratios projectiles(forward penetration) |
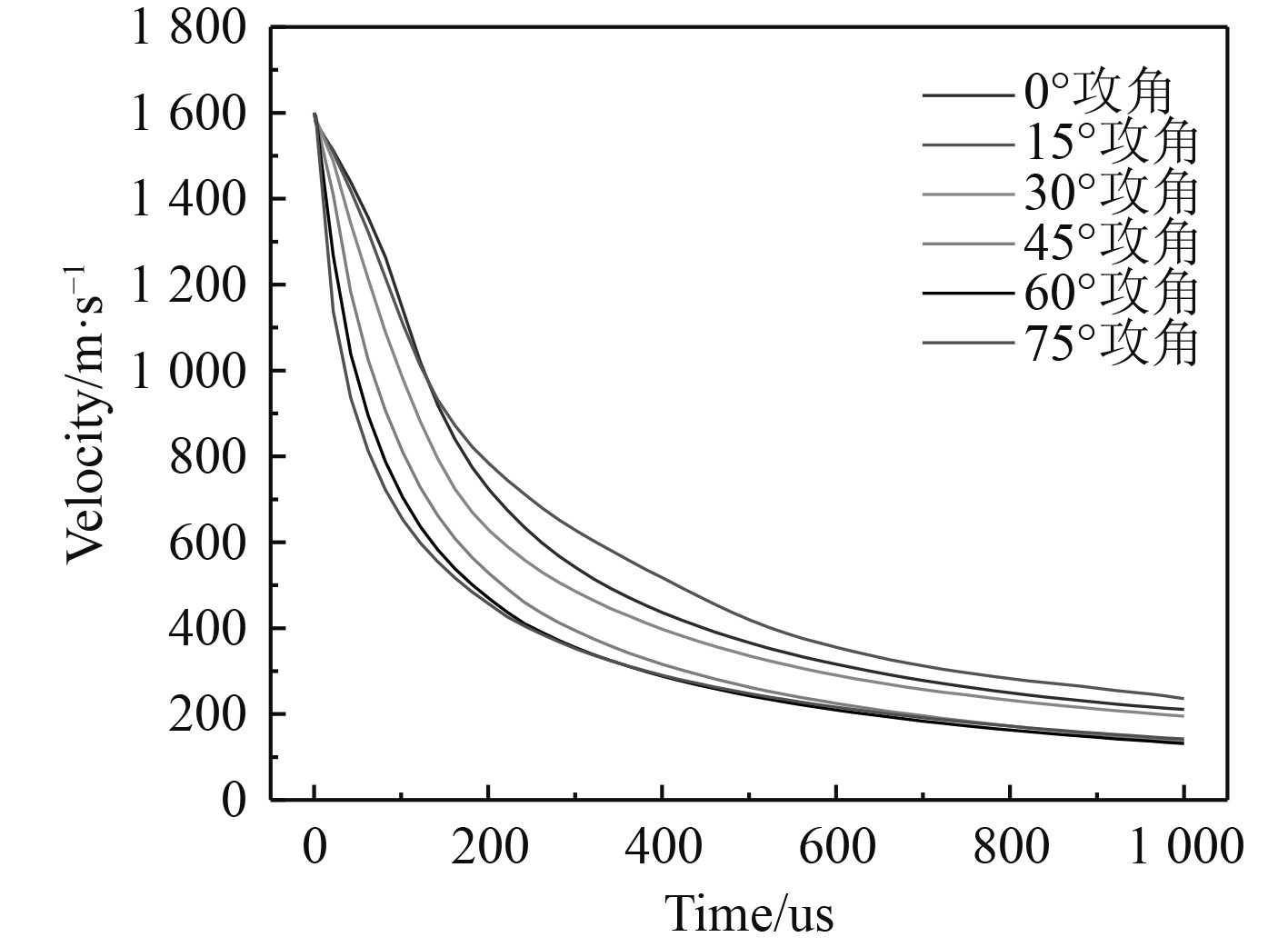
由图5可看出,在入水初期,初始攻角越大的弹体,其速度衰减越快,正侵彻入水100 μs后剩余速度为1 142 m/s,而75°攻角入水时剩余速度仅为652 m/s。这是由于带攻角弹体在水中运动时,攻角越大,与水介质的接触面积越大,其受到的阻力更大,速度衰减更快;当入水一段时间后,弹体速度较慢,且弹体受水介质侵蚀产生墩粗变形、弹体均翻转至最大迎流面,其阻力系数又发生改变,不同攻角的弹体衰减速率趋于一致。
|
图 5 不同攻角下时间-速度曲线 (V=1 600 m/s,h/d=4.95) Fig. 5 Curves of time-velocity at different attack angles ( V=1 600 m/s,h/d=4.95) |
分别计算弹体以1 600 m/s、800 m/s、400 m/s速度下各种攻角入水的状况。读取弹体入水后1000 μs的速度,并定义
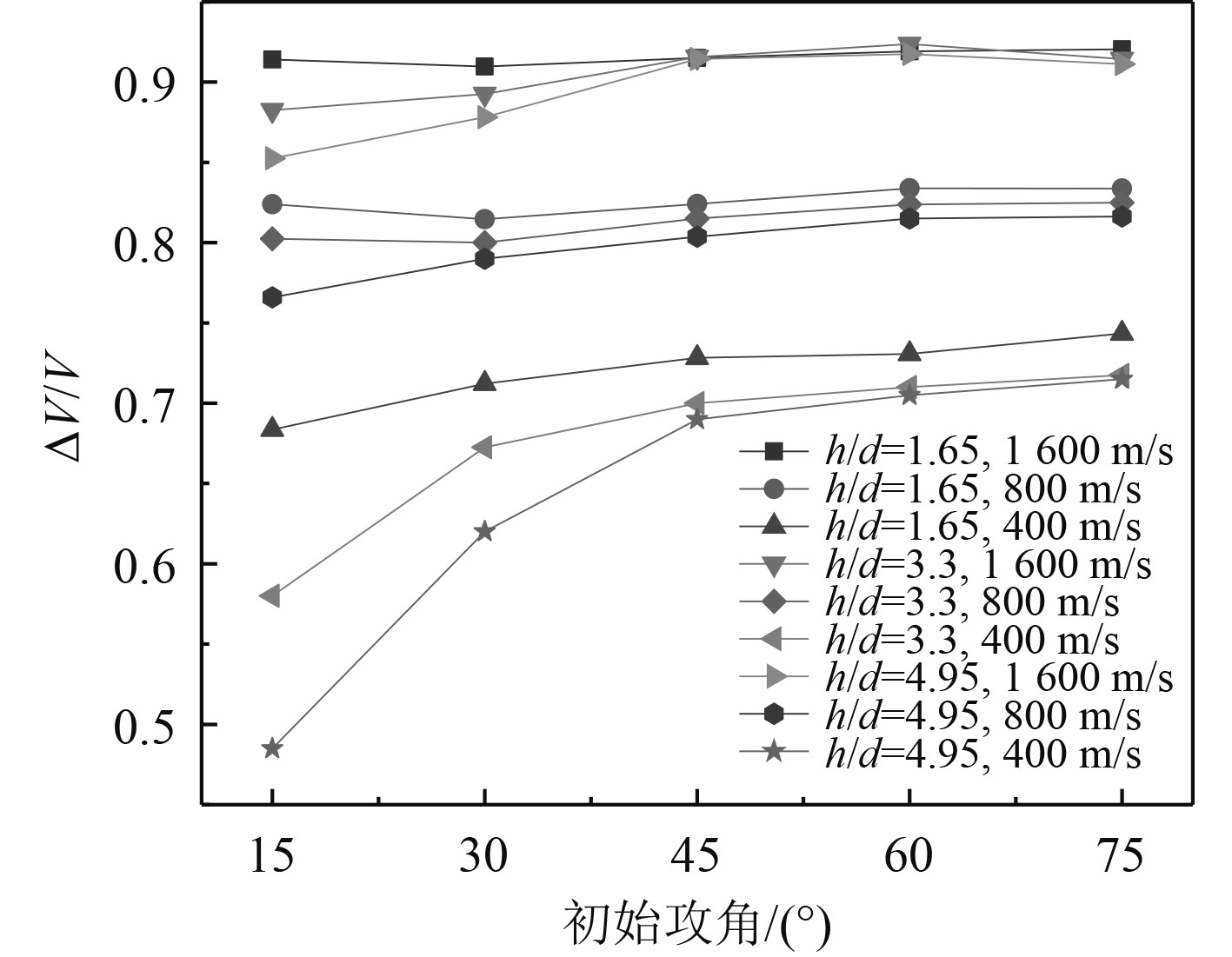
由图6可知,弹体入水速度、初始攻角和长径比对弹体速度衰减有不同程度的影响。其中入水速度的影响最大,入水速度越高,在相同时间内弹体降速比例越高,说明水介质对高速弹体有更好的降速效果;而初始攻角在速度较低、攻角较小时有较为显著的影响,此时弹体的降速比例则呈现随攻角增大而增加的趋势,而攻角较大或弹速较高时,弹体攻角的变化对弹体降速比例没有明显变化;而弹体长径比越大,对弹体攻角变化越敏感,尤其在弹体低速、小攻角情况下,长径比大的弹体随着初始攻角的增大,弹体降速比例迅速增大。
|
图 6 初始攻角-降速比例 Fig. 6 Curve of attack angle - deceleration ratio |
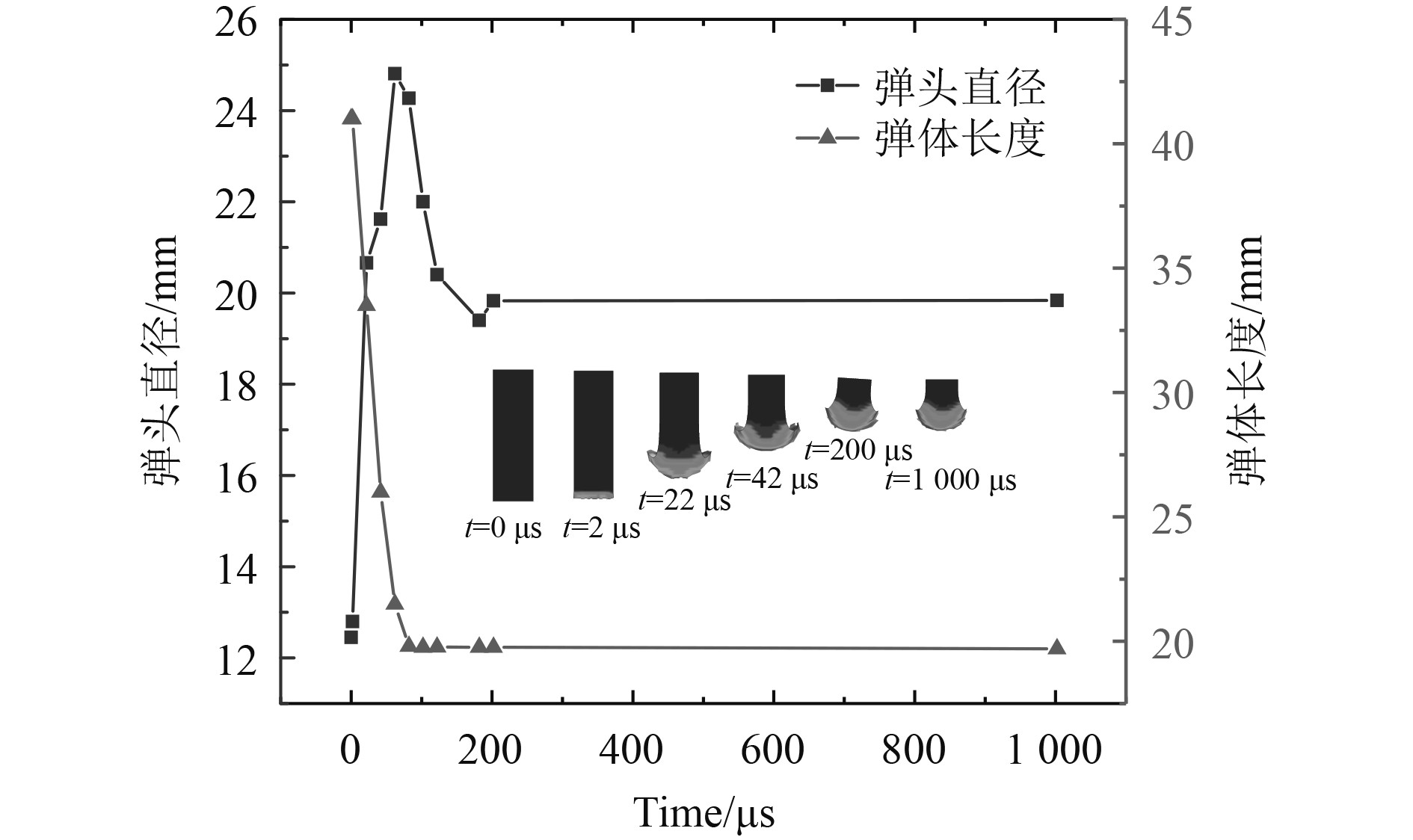
分析长径比为3.3弹体正侵彻入水情况。当弹体以1 600 m/s的初速度正侵彻水箱,弹体2 μs时接触前面钢板,会在弹体内部及靶板内产生压缩波,弹性压缩波传播要比塑性压缩波快。当弹体内弹性压缩波传播到弹尾并反射回一道卸载波,卸载波在弹头与塑性压缩波相遇互相抵消,所以弹体仅在头部位置会发生塑性变形,产生一定的墩粗,而弹尾基本不发生变形。墩粗后的弹体紧接着高速入水,此过程中弹体头部始终挤压、碰撞水介质,且作用时间长,从而使弹头进一步发生侵蚀、墩粗变形,弹头逐渐变形成蘑菇头形状,且蘑菇头附近弹体逐渐被侵蚀,弹体质量逐渐减小。由图7可看出,初始时刻弹体头部变形较大,前60 μs内弹体长度大量侵蚀且产生蘑菇头,此阶段弹体长度呈线性快速减小,而弹头被水介质挤压、碰撞形成蘑菇头,且蘑菇头直径一直增大,在60 μs时达到最大值。此后随着弹速在水中速度逐渐降低,弹体侵蚀也逐渐减小,80 μs后弹体长度基本保持不变,表明此时的弹速不足以使弹体在长度方向继续侵蚀变形。弹头直径在60 μs后开始减小是由于弹头的侵蚀不继续增加,而已经产生的蘑菇头边界位置是由水体侵蚀形成的,其强度较为脆弱,在水的挤压冲击下会逐渐被侵蚀掉与弹体分开,所以弹头直径在60 μs后开始减小。当边界位置被侵蚀完后,由于弹速较低无法继续侵蚀弹体主体,弹头直径保持不变,弹体最终形成侵蚀-蘑菇头变形。即在弹体入水初期,弹体受到大量侵蚀和墩粗,之后弹体变形速率逐渐变低,当弹速降到一定程度时,弹体基本不发生墩粗变形与侵蚀。
|
图 7 弹体变形形貌及曲线图(h/d=3.3, v=1 600 m/s) Fig. 7 Deformation morphology and curve of projectile(h/d=3.3, v=1 600 m/s) |
当弹体带攻角入水时,弹体的破坏变形形貌是弹体初速度和攻角耦合影响的结果,弹体会产生侵蚀变形、墩粗变形、弯曲变形及3种变形模式的耦合。如图8所示,在弹体初始速度较低时,弹体只会发生墩粗变形,正侵彻时产生较为对称的墩粗变形,带攻角入水时则产生非对称墩粗。当弹体速度在中高速时,弹头产生一定的蘑菇头变形。当有攻角存在时,弹体侧面会受到水介质侵蚀产生变形,且蘑菇头形状呈非对称性,即呈现侧面侵蚀-非对称蘑菇头变形。当弹体速度达到高速时,弹体受冲击载荷大,触水位置发生较大的侵蚀破坏,正侵彻时弹体轴向长度大幅减少,弹头墩粗呈蘑菇头状,弹体带较小攻角时,弹体受不对称的横向载荷产生塑性弯曲,发生侵蚀-整体塑性弯曲变形。当攻角角度较大时,弹体侧面成为主要触水位置,弹体侧面发生大范围侵蚀变形。

|
图 8 弹体的不同破坏形貌 Fig. 8 Different damage morphologies of the projectile body |
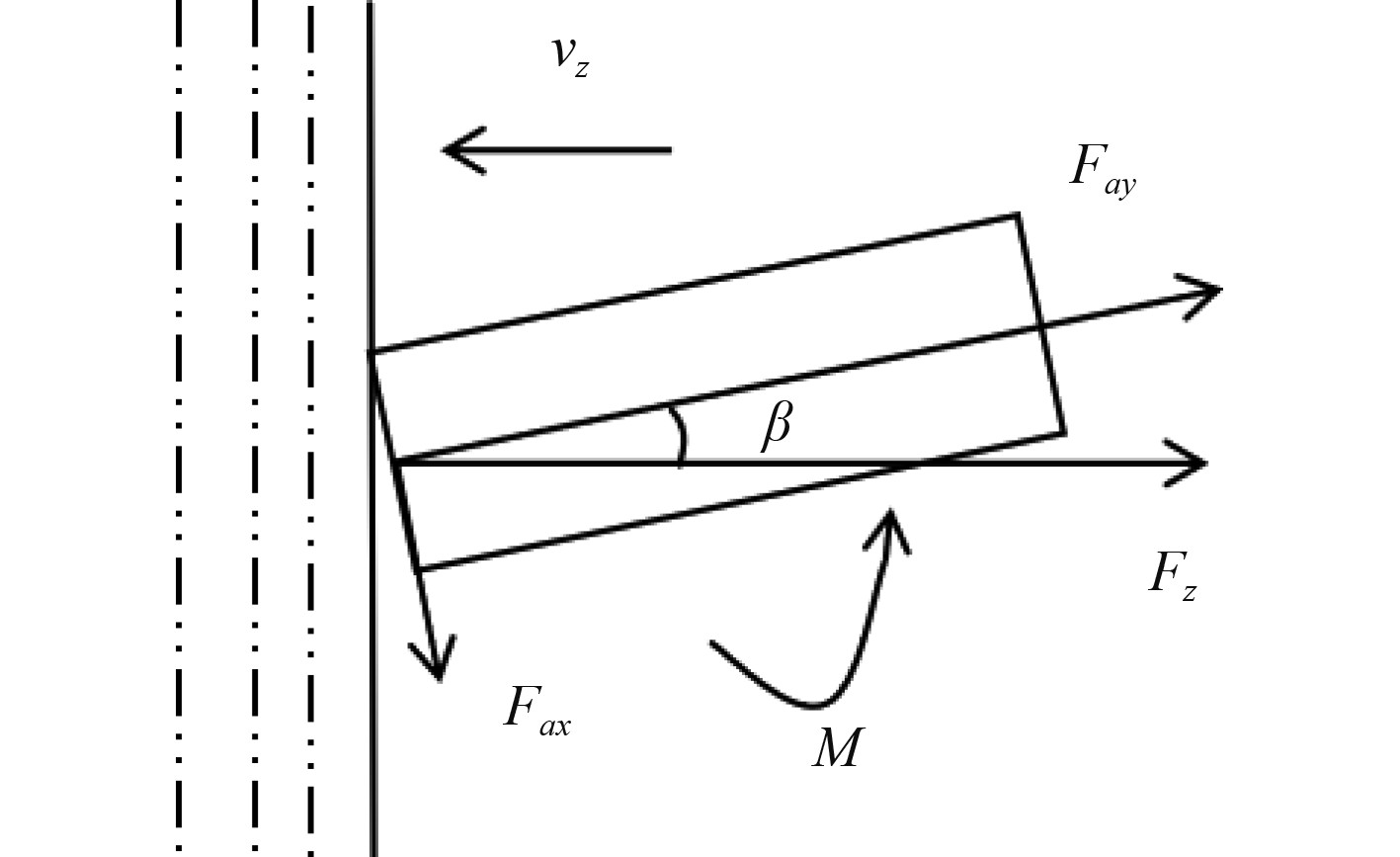
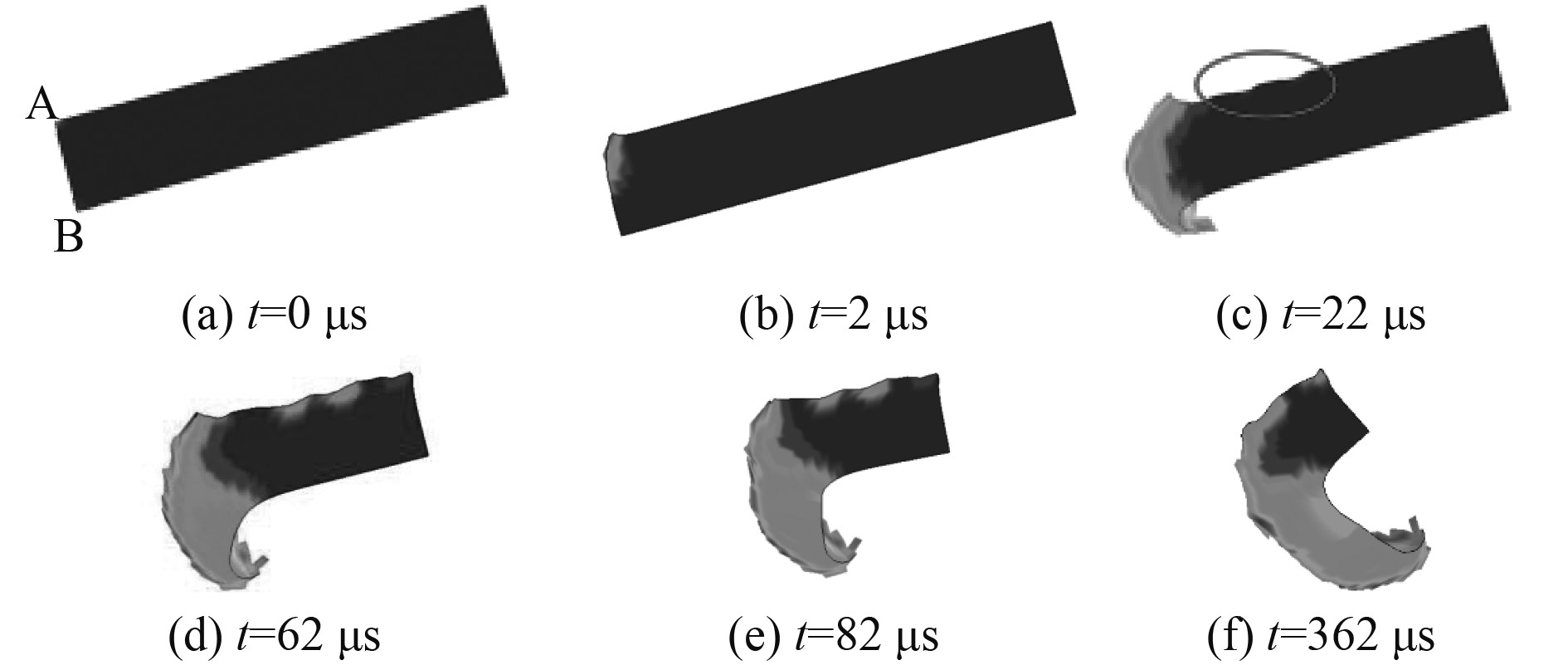
如图9所示,当弹体以一定攻角高速入水时,弹体受到水介质给与的水平于速度方向的阻力,可以分解为沿弹体轴向和垂直弹体2个方向的力,垂直于弹体轴向的分力会给与弹体一个翻转力矩,且在弹体截面产生弯曲应力。图10为弹体以1 600 m/s、带15°攻角入水不同时间的变形形貌,撞击阶段弹头一侧会先接触钢板,接触位置发生墩粗变形。进入水介质后,弹体接触水介质的面积并不均衡,弹头A点首先接触水介质,受到最大的冲击力,由于A为弹体边界,受到垂直冲击发生变形的面积较小,而由于入水姿态的影响,A点以下弹头部分有较大面积产生变形,所以弹头下侧产生较明显的蘑菇头变形。入水初期,由于弹头产生蘑菇头的非对称性,弹头下侧产生较大蘑菇头变形,阻挡了水对弹体下侧的侵蚀,而弹体上侧由于没有弹头的阻挡,则会与水介质接触,产生变形,见图10(c)。由于弹头下侧产生的蘑菇头变形更大,所以下侧与水介质接触的面积更大,弹体受到不对称的载荷影响增大,在横截面上产生更强的弯曲应力,弹体截面在轴向载荷和弯曲应力的共同作用下达到屈服极限,屈服条件为:
|
图 9 弹体入水受力示意图 Fig. 9 Schematic diagram of force of projectile body entering water |
| $ \frac{\left|{F}_{{ay}}\right|}{\left|{N}_{Y}\right|}+\frac{\left|M\right|}{\left|{M}_{Y}\right|}>1 。$ | (6) |
式中:Fay为轴向载荷;M为弯矩载荷;NY和MY分别为截面的屈服极限。此时弹体危险截面将产生塑性铰,使弹体产生塑性弯曲变形。随着弹体的转动,弹体塑性铰也随着移动,弯曲截面逐渐向后移动,直至截面载荷不足以产生塑性屈服,所以弹体高速非理想侵彻过程中,会发生侵蚀-整体塑性弯曲变形。
|
图 10 15°攻角弹体入水形貌变化 Fig. 10 Deformation morphology of projectile body entering water at 15° angle of attack |
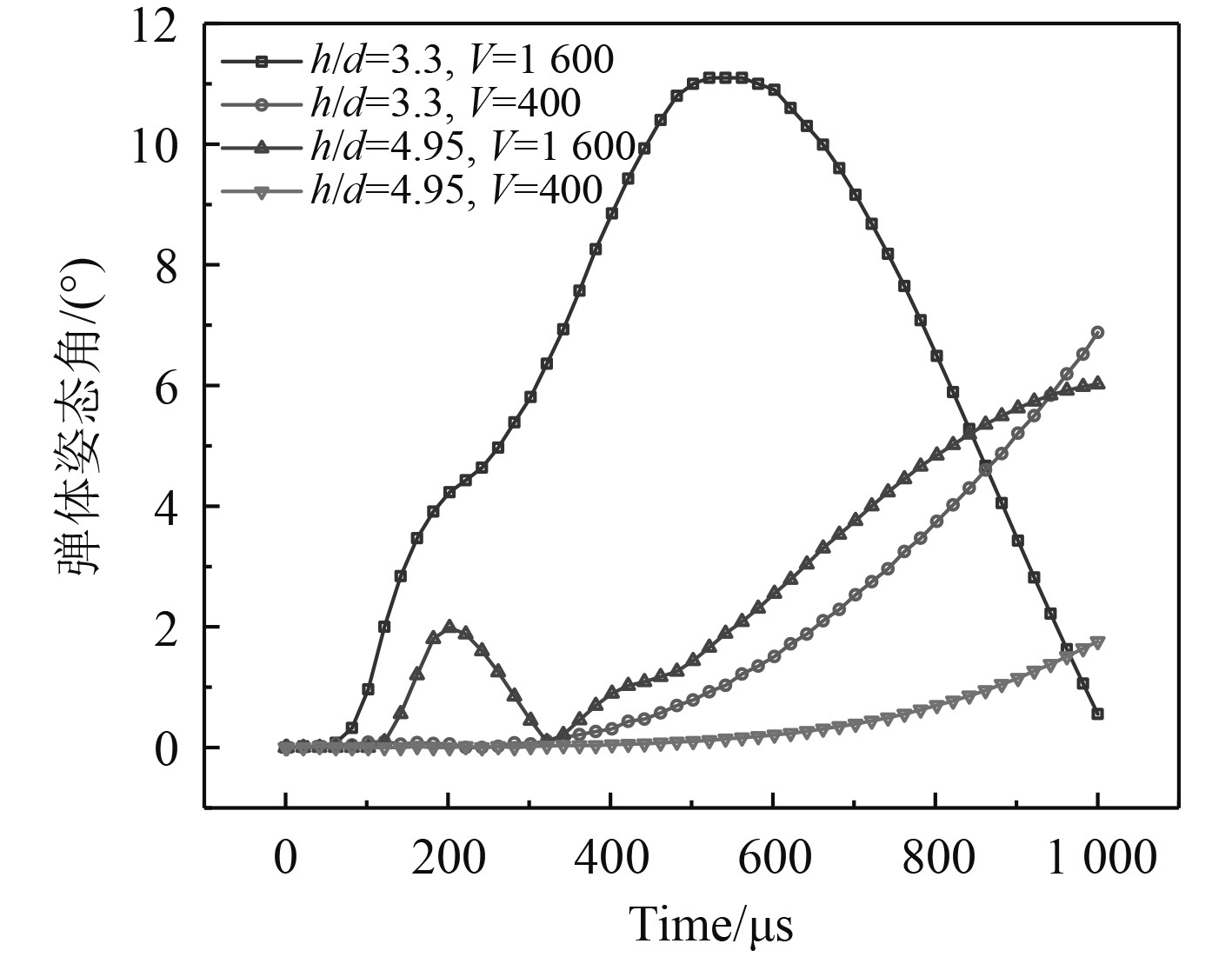
弹体入水后的受力十分复杂,不仅受到水流的阻滞力,还受到重力与水中压强的影响。弹体垂直入水时由于自由液面的存在,其给与弹体的压力远小于箱底的压力,导致弹体上下受力不平衡,排开的水量不同,产生不对称的空泡。由于空泡的存在,主要是弹头与水介质接触,弹头受到上下不对称的力,则会对弹体质心产生偏转力矩,弹体下侧受力更大则产生顺时针的力矩,弹体偏转呈现抬头姿态。而当弹体姿态向上偏转一定程度时,其头部在速度方向上与水介质接触面积增大,即上侧受力增大,弹体受到逆时针的偏转力矩,发生二次偏转。由图11可知,入水速度更高的弹体更早出现弹体姿态的偏转,这是由于入水速度高时弹头变形较大,与水介质接触面积更大,其受力更不均衡。而长径比较小的弹体由于其转动惯量较小,其姿态偏转较长杆弹出现的更早,且姿态改变更大。
|
图 11 正侵彻下弹体偏转角度曲线 Fig. 11 Deflection angle curve of projectile body under forward penetration |
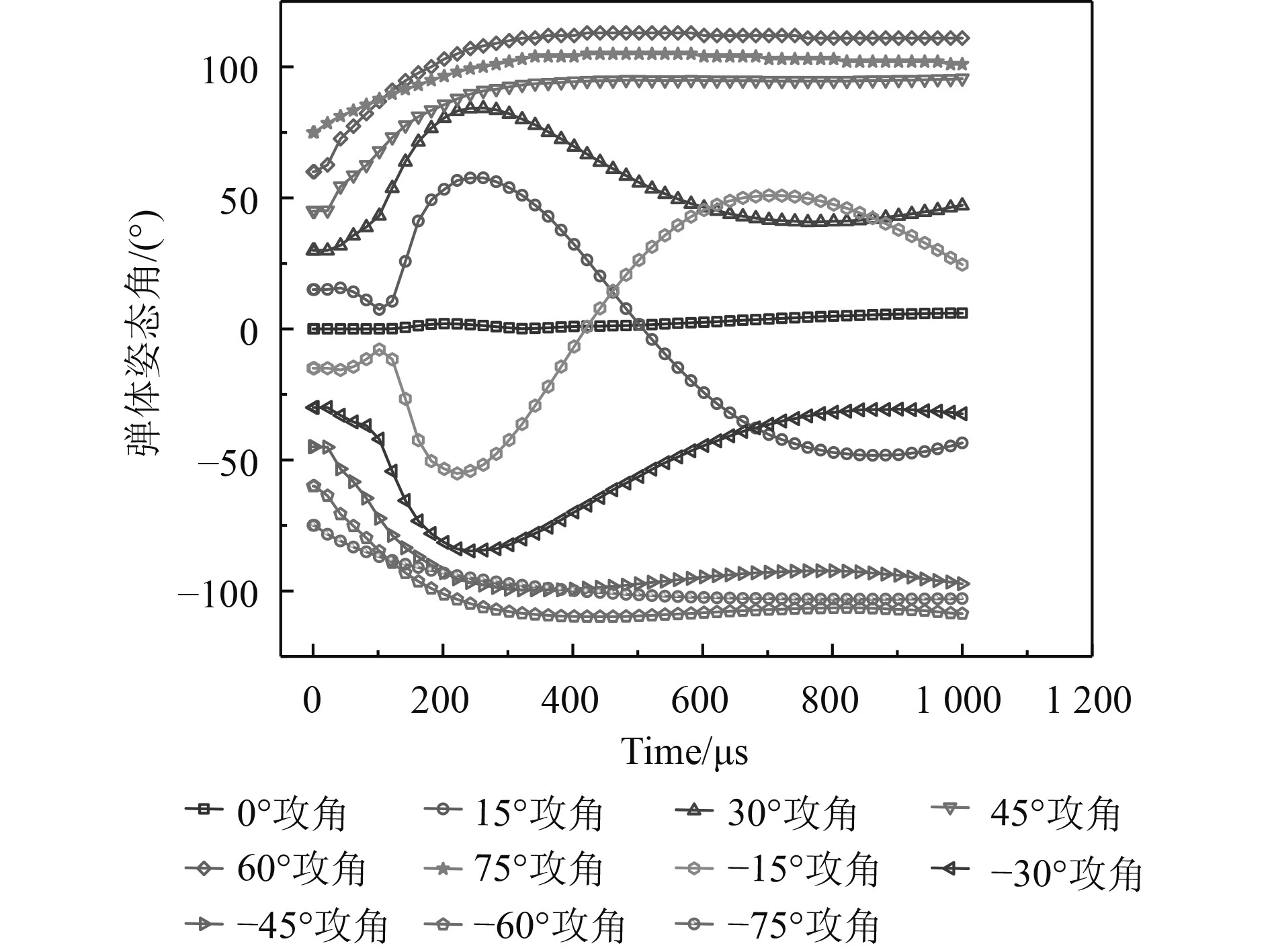
而当弹体带初始攻角时,由于弹头为主要受力部位且受力方向与质心不重合,会产生偏转力矩,弹体也会发生姿态偏转。初始攻角较小时,弹体也会发生二次偏转现象;弹体初始攻角较大时,弹体在发生一定转动后便达到最大迎流面。此时弹体姿态基本维持稳定,不再发生大幅度转动,而在一定范围内小幅度震荡。
|
图 12 弹体姿态角随时间变化关系(h/d=4.95,v=1 600 m/s) Fig. 12 Variation relation of projectile attitude angle with time(h/d=4.95,v=1 600 m/s) |
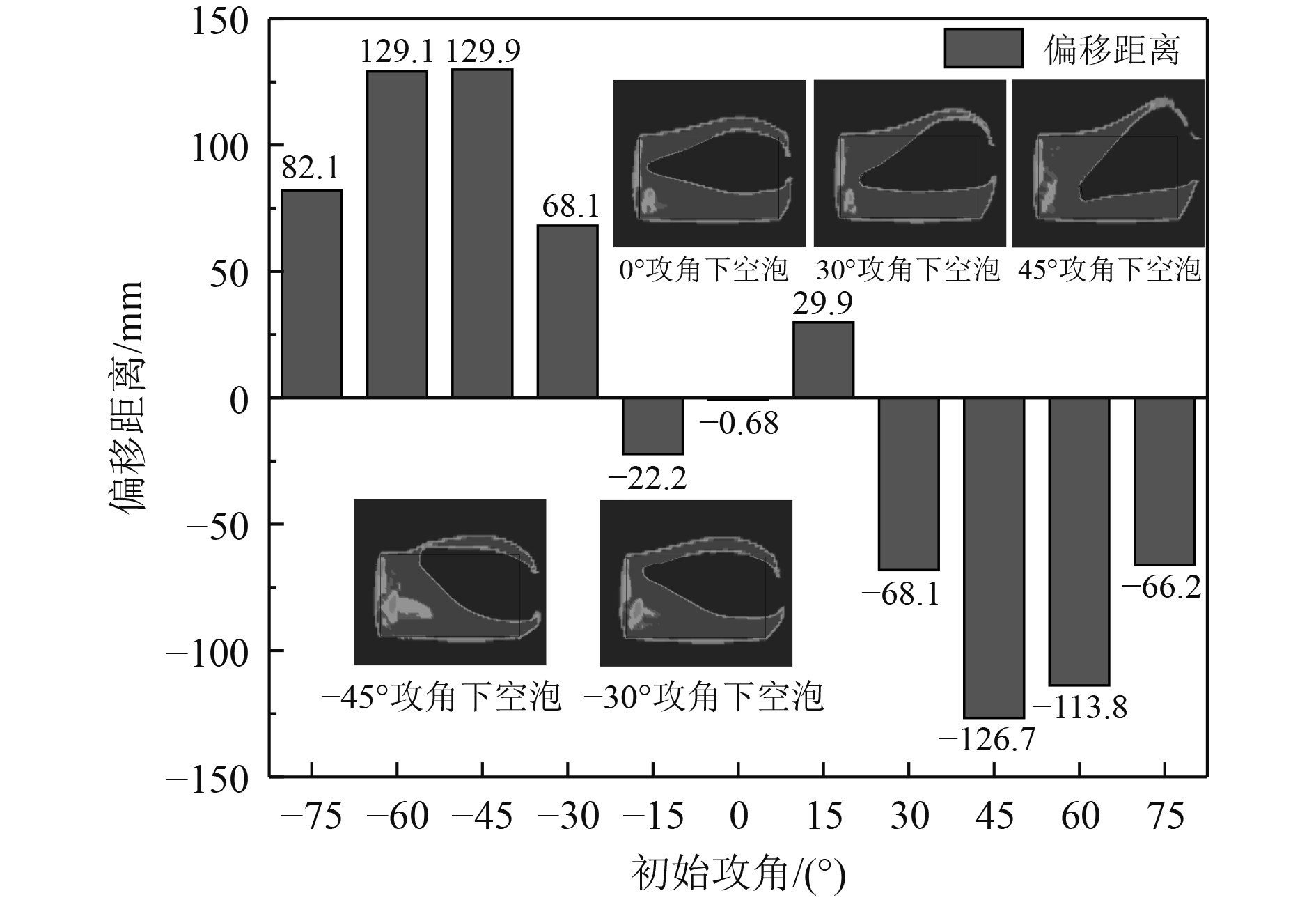
弹体带攻角入水不仅会产生姿态偏转,还会发生弹道轨迹的偏移。由图13可知,攻角是弹体偏移的关键因素,攻角的正负决定了弹体的偏移方向,攻角的大小也决定了偏移距离的大小。带攻角弹体在水中偏移距离要大于正侵彻入水,在一定范围内,随着攻角的增大,弹体一侧与水介质接触面积增大,而另一侧受空泡影响不与水介质接触,因此弹体两侧受力不平衡增大,偏移距离逐渐增大;但是攻角达到75°时,偏转距离突然减小,这是因为过大的攻角导致弹体性质改变,原先圆柱弹体的侧面变为弹头,而原先的弹头弹尾变为弹体的两侧。此时可视为此种形状的弹体带15°攻角入水,所以弹体在垂直方向上的分量减小,弹体偏转距离有所减小。
|
图 13 攻角-偏移距离 Fig. 13 Curve of attack angle - deflection distance |
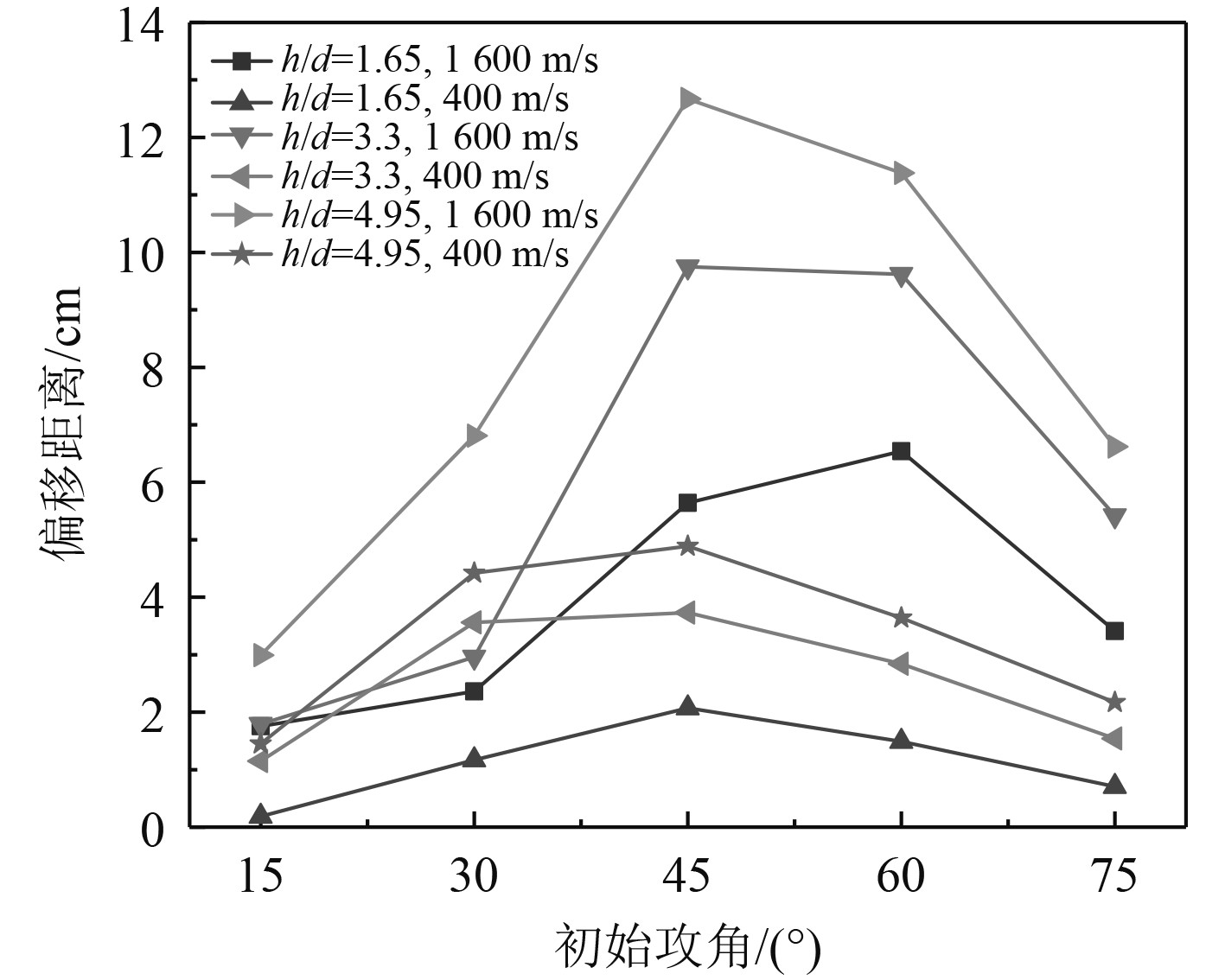
比较不同长径比、不同初始速度弹体入水后的偏移距离,如图14所示。可以发现,长径比4.95、初始速度1 600 m/s的弹体在各个攻角下偏移距离都是最大的,而长径比为1.65、初始速度为400 m/s的弹体偏移距离最小。则长径比越大、初始速度越大的弹体的偏移距离越大。由于初始速度越大,其受力向偏移方向产生的分速度便越大,则相同时间内偏移距离更大。而长径比越大 ,由于攻角的存在,其与水介质接触面积大,则其在纵向方向上受力更大,有更大的偏移距离。
|
图 14 初始攻角-偏移距离曲线图 Fig. 14 Curve of attack angle - maximum deflection distance |
本文通过LS-DYNA有限元软件,对不同攻角下长杆弹入水侵彻进行数值计算,借助数值计算的结果,对带攻角弹体的速度特性、入水姿态变化及弹道偏航进行分析,着重分析了攻角、长径比对弹体姿态的影响。得到主要结论如下:
1)弹体入水可以分为入水阶段、翻转阶段和稳定阶段。即弹体在入水后会产生姿态翻转,经过一段时间后弹体姿态趋于稳定。攻角较小时,弹体在翻转阶段会有二次偏转现象,而攻角较大时只产生一次偏转。
2)攻角越大,弹体的衰减速率越快。弹体高速情况下攻角对弹速的影响较小,低速时攻角对弹速有显著影响。且长杆弹对攻角的变化更为敏感
3)弹体非理想入水会产生很强的冲击力使弹体产生非对称墩粗、侵蚀。低速时,弹体变形以墩粗为主;中高速时,弹体发生蘑菇头状,而高速时,弹体发生很大的侵蚀及墩粗变形。当速度达到一定值时,弹体甚至发生整体塑性弯曲变形。
4)长径比小的弹体其破坏能力较小,弹道偏航较小,但姿态偏转较大;长径比较大的弹体破坏能力强,弹体姿态偏转较小,但弹道偏航距离较大。
| [1] |
朱锡, 张振华, 刘润泉, 等. 水面舰艇舷侧防雷舱结构模型抗爆试验研究[J]. 爆炸与冲击, 2004, 24(2): 133-139. ZHU X, ZHANG Z H, LIU R Q, et al. Experimental study on the explosion resistance of cabin near shipboard of surface warship subjected to underwater contact explosion[J]. Explosion and Shock waves, 2004, 24(2): 133-139. DOI:10.3321/j.issn:1001-1455.2004.02.006 |
| [2] |
卢芳云, 李翔宇, 林玉亮, 战斗部结构与原理[M], 北京: 科学出版社, 2009
|
| [3] |
张凯奇. 水下EFP及其终点效应的研究[D]. 太原: 中北大学, 2020.
|
| [4] |
吴凡达. 聚能-爆破战斗部对潜艇多层壳体毁伤效应研究[D]. 太原: 中北大学, 2020.
|
| [5] |
陈兴, 周兰伟, 李福明, 等. 杆式射流对充液防护结构的毁伤机理及影响因素的数值模拟[J]. 高压物理学报, 2021, 35(2): 145-155. CHEN X, ZHOU L W, LI F M. et al. Numerical simulation on damage mechanism and influencing factors of JPC shaped charge on liquid-filled defensive structure[J]. Chinese Journal of High Pressure Physics, 2021, 35(2): 145-155. DOI:10.11858/gywlxb.20200626 |
| [6] |
王雅君, 李伟兵, 王晓鸣, 等. EFP水中飞行特性及侵彻间隔靶的仿真与试验研究[J]. 含能材料, 2017, 25(6): 459-465. WANG Y J, LI W B, WANG X M, et al. Numerical simulation and experimental study on flight characteristics and penetration against spaced targets of EFP in water[J]. Chinese Journal of Energrtic Materials, 2017, 25(6): 459-465. DOI:10.11943/j.issn.1006-9941.2017.06.003 |
| [7] |
吴子奇. 弹目结合的反舰导弹对目标舰船靶标侵彻毁伤研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [8] |
杨莉, 张庆明, 巨圆圆. 爆炸成型弹丸对含水复合装甲侵彻的实验研究[J]. 北京理工大学学报, 2009, 29(3): 197-200. YANG L, ZHANG Q M, JU Y Y. Experimental study on the penetration of explosively formed projectile against water-partitioned armor[J]. Transactions of Beijing Institute of Technology, 2009, 29(3): 197-200. DOI:10.15918/j.tbit1001-0645.2009.03.007 |
| [9] |
许通通. 串联聚能装药水下作用研究[D]. 北京: 北京理工大学, 2017.
|
| [10] |
SONG Z J, DUAN W Y, XU G D, et al. Experimental and numerical study of the water entry of projectiles at high oblique entry speed[J]. Ocean Engineering, 2020, 211: 107574. DOI:10.1016/j.oceaneng.2020.107574 |
| [11] |
CHEN C , X YUAN, X LIU, et al. Experimental and numerical study on the oblique water-entry impact of a cavitating vehicle with a disk cavitator[J]. International Journal of Naval Architecture and Ocean Engineering, 2018, 11.
|
| [12] |
CHEN C, YUAN X, LIU X, et al. Experimental and numerical study on the oblique water-entry impact of a cavitating vehicle with a disk cavitator[J]. International Journal of Naval Architecture and Ocean Engineering, 2019, 11(1): 482-494. DOI:10.1016/j.ijnaoe.2018.09.002 |
| [13] |
李天雄. 入水弹道转向的特性研究[D]. 南京: 南京理工大学, 2020.
|
| [14] |
MIRZAEI M, TAGHVAEI H, ALISHAHI MM. Mathematical modeling of the oblique water-entry of cylindrical projectiles[J]. Ocean Engineering, 2020, 205: 107257. DOI:10.1016/j.oceaneng.2020.107257 |
| [15] |
ALEKSEEVSKII V P. Penetration of a rod into a target at high velocity. Combustion, Explosion, and Shock Waves, 1966, 2: 63-66.
|
| [16] |
TATE A. A theory for the deceleration of long rods after impact. Journal of the Mechanics & Physics of Solids, 1967, 15: 387-399.
|
| [17] |
GAO S, LI D, HOU H, et al. Investigation on dynamic response of liquid-filled concave cell structures subject to the penetration of high-speed projectiles[J]. Thin-Walled Structures, 2020, 157(2): 107119. |
| [18] |
仲强, 侯海量, 李典, 等. 陶瓷/液舱复合结构抗侵彻机理试验研究[J]. 船舶力学, 2017, 10(21): 1282-1290. ZHONG Q, HOU H L, LI D. et al. Experimental study on anti-penetration mechanism of ceramic/fluid cabin composite structure[J]. Journal of Ship Mechanics, 2017, 10(21): 1282-1290. DOI:10.3969/j.issn.1007-7294.2017.10.012 |
| [19] |
李典, 朱锡, 侯海量, 等. 高速杆式弹体侵彻下蓄液结构载荷特性的有限元分析[J]. 爆炸与冲击, 2016, 36(1): 1-8. LI D, ZHU X, HOU H L, et al. Numerical analysis of energy Dissipation mechanism of liquid -filled structure subjected to high velocity rod projectile penetration[J]. Explosion and Shock Waves, 2016, 36(1): 1-8. DOI:10.11883/1001-1455(2016)01-0001-08 |
| [20] |
李典, 侯海量, 朱锡, 等. 高速杆式弹侵彻下蓄液结构耗能机理数值分析[J]. 海军工程大学学报, 2018, 30(2): 60-65. LI D, ZHU X, HOU H L. Finite element analysis of load characteristic of liquid- filled structure subjected to high velocity long- rod projectile penetration[J]. Journal of Naval University of Engineering, 2018, 30(2): 60-65. |
| [21] |
李典, 朱锡, 侯海量. 高速杆式弹侵彻下蓄水结构防护效能数值分析[J]. 海军工程大学学报, 2015, 27(4): 21-25+30. LI D, ZHU X, HOU H L. Numerical analysis of protective efficacy Of water-filled structure subjected to high velocity long-rod projectile penetration[J]. Journal of Naval University of Engineering, 2015, 27(4): 21-25+30. |
| [22] |
朱珠, 袁绪龙, 刘维. 柱体大攻角入水弹道建模与仿真[J]. 火力与指挥控制, 2015, 40(2): 13-18+23. ZHU Z, YUAN X L, LIU W. On modeling and simulation of cylinder droppling in water with high angle of attack[J]. Fire Control & Command Control, 2015, 40(2): 13-18+23. DOI:10.3969/j.issn.1002-0640.2015.02.005 |
| [23] |
汪振, 吴茂林, 戴文留. 大口径弹体高速入水载荷特性研究[J]. 弹道学报, 2020, 32(1): 15-22. WANG Z, WU M L, DAI K L. Study on load characteristics of high-speed water-entry of large caliber projectile[J]. Journal of Ballistics, 2020, 32(1): 15-22. |
| [24] |
吴晓光, 李典, 吴国民, 等. 高速杆式弹侵彻下蓄液结构的防护能力[J]. 爆炸与冲击, 2018, 38(1): 76-84. DOI:10.11883/bzycj-2016-0146 |
 2023, Vol. 45
2023, Vol. 45
